基于改進二叉樹支持向量機的多故障分類算法

李偉偉，王 莉，張 琳，劉 進

（1.空軍工程大學防空反導學院，陜西 西安 710051；2.解放軍95425部隊，云南 曲靖 655000）

0 引言

支持向量機（SVM）是基于統計學習理論的新學習方法［1］，最初用于解決二值分類問題，但現實中多分類問題居多。因此，將二值分類算法推廣到多分類領域是當前SVM 研究的重要內容之一［2］。SVM 的多分類擴展策略主要分兩大類：一是整體優化法，將所有SVM 參數優化在一個公式中，該方法求解復雜，解決多分類問題很少應用；二是組合學習法，將SVM 按不同策略組合成多類分類器，例如一對多法、一對一法、決策導向無環圖法和二叉樹法等［3］。一對多法運算量過大，一對一法所需SVM數目過多，決策導向無環圖法存在決策偏好的問題，二叉樹法結構的設計會影響多類分類器的分類精度［4］。

目前，對于二叉樹支持向量機算法結構設計的問題已有一定研究。文獻［5-6］根據各類樣本在高維特征空間的分布情況設計分類順序，分布范圍廣的類型首先被識別，就是先把樣本空間中最容易識別的類型識別出來。另外，一種依賴類別優先級的多類分類器可根據各類型發生頻率的高低排序確定二叉樹的結構，即發生概率較高的類別先被識別出來。但上述算法僅考慮了某一種影響因子對分類精度的影響，不夠客觀、全面，因此分類器的結構不能使分類精度達到最優。本文針對上述問題，提出了將AHP和二叉樹SVM 相結合的多故障分類算法。

1 AHP和二叉樹SVM 的基本原理

1.1 AHP

層 次 分 析 法（Analytic Hierarchy Process，AHP）是美國著名運籌學家Satty 等人于20 世紀70年代提出的一種定性與定量分析相結合的多準則決策分析方法。基本思想是把決策問題的相關元素按照支配關系形成層次結構，將評估目標分解成一個多級指標，并通過引入1～9的比例標度對各個因素的相對重要性給出判斷［7］。表1 為不同比例標度的含義。

表1 判斷矩陣的比例標度Tab.1 Proportion scale of judgment matrix

層次分析法通過將復雜問題分解為若干層次和若干因素，在各因素之間進行簡單的比較和計算，得出不同方案的權重，為最佳方案的選擇提供依據［8］。實施步驟主要有明確問題，建立遞階層次結構，構造判斷矩陣，計算權重值，進行一致性檢驗，得到各方案對總目標的權重值。

層次分析法不僅能夠綜合考慮評價體系中各層因素的重要程度使各指標權重趨于合理，而且更大的優勢在于能夠充分利用專家的主觀意見。

1.2 二叉樹SVM

二叉樹SVM 分類原理如下：首先通過構造二叉樹將多分類問題分解成一系列二值分類問題，然后使用SVM 實現二分類。二叉樹SVM 進行訓練和測試時，從根節點的SVM 開始分類，按照一定的分類順序依次識別。假如有1，2，…，k種模式，對k種模式進行分類，需k-1個SVM，結構如圖1所示。

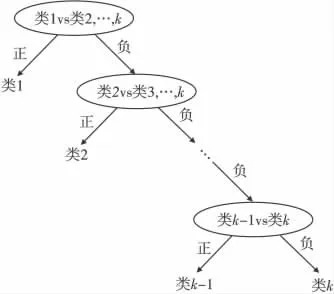
圖1 二叉樹SVM 結構Fig.1 Structure of binary tree SVM

二叉樹SVM 對于測試樣本無需經過所有二值分類器，只要識別出類別即可停止運算，從而節省了測試時間。在圖1 所示分類器中，第1 個SVM 用于將第1類從1，2，…，k 類別中區分出來，第2 個SVM 將第2類從2，3，…，k 類別中區分出來，依此類推，直到第k-1 個SVM 將最后兩個類別區分開。圖1所示分類器只是許多分類策略中的一種，分類順序為1，2，…，k，共有k！種分類順序，分別對應k！種結構，不同的二叉樹結構決定了不同的分類精度。將分類器用于模式識別時，可通過合理設計二叉樹的結構提高分類器的分類精度。

2 基于AHP和二叉樹SVM 的算法

基于AHP 和二叉樹SVM 的多故障分類算法中，AHP綜合多個指標衡量所有故障的價值度，對每一類故障得出一個權重值，權重大小決定了故障識別的先后順序，基于此順序構建二叉樹SVM 的結構。

2.1 結構設計對分類精度的影響

二叉樹支持向量機的結構并不是唯一的，不同的結構會導致不同的分類結果和分類精度。結構設計如何影響分類精度，下面簡單分析之。

以圖1為例，假設各層劃分正確率分別為p1，p2，…，pk，類別劃分正確率為l，則所有故障類別的劃分正確率為：

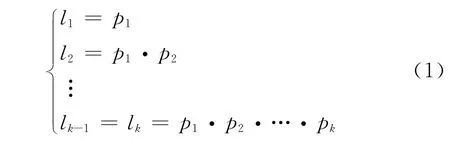
由式（1）可得

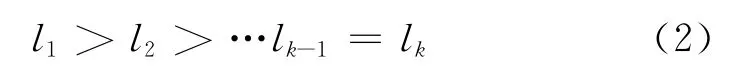
即二叉樹分類器越底層，SVM 識別正確率越低；而且下層SVM 識別率依賴于上層，只有使上層SVM 識別正確，下層SVM 的識別率才能得到保證。

基于此特點，只有保證識別率高的類別處于分類器上層，才能總體上提高整個分類器的分類精度。先將樣本空間中最易被分割的類識別出來以及采用最大投票機制算法構造二叉樹都是基于此原因。

因此，本文改進算法通過建立一套評價體系為各類別設定權重值，根據權重值對所有類別排序，使權重大的類別處于分類器的上層，符合上述特點。這樣確定下來的二叉樹結構依賴于各個類別的權重量，相比較隨機確定的二叉樹結構，具有更好的分類性能。

2.2 基于AHP和二叉樹SVM 的多故障分類算法

為了便于問題說明，直接以發電機軸承的故障診斷作為案例闡述改進算法，主要步驟如下：

1）建立層次結構

對于電機軸承的故障診斷問題，在高維特征空間中，影響分類精度的因素主要有類內樣本分布范圍、類間樣本分布距離等因素。其中，類內樣本分布范圍指同一類別樣本在高維特征空間的分布范圍，范圍越大，被識別的概率越高；類間樣本分布距離指在高維特征空間中，不同類別分布范圍之間的距離，兩者距離越大，越容易被分割開。結合實際經驗進行診斷時，還需要考慮故障發生概率、診斷故障后的挽回損失等。

層次分析法模型分為目標層、準則層和方案層，其中，目標層為故障的價值度；準則層為衡量故障的影響因子：各種故障在高維特征空間的樣本分布范圍B1，故障發生的頻率B2，診斷挽回的損失B3以及各類故障在高維特征空間樣本的類間分布距離B4，多個影響因子的選擇使得到的權重是故障識別率，實際發生概率，理論分割難易程度的集中體現；方案層故障狀態包括：正常、內圈故障、外圈故障、滾珠故障。層次結構如圖2所示。

2）構造判斷矩陣

為把定性分析的結果量化，將同層次元素對于上層某一準則的重要性進行兩兩比較，構造判斷矩陣

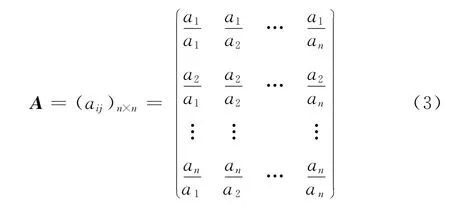
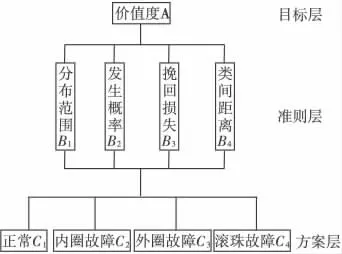
圖2 軸承故障診斷的層次結構圖Fig.2 Hierarchical structure of bearing fault diagnosis

式（3）中，aij是元素ai和aj相對于準則層的重要性的比值，判斷矩陣A 具有下列性質：

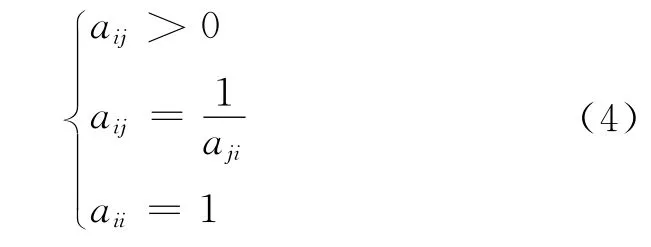
同層次元素的重要程度如何，根據表1中程度的不同按1～9的比例標度賦值。本文軸承故障中，基于診斷經驗構造準則層B 相對目標A 的判斷矩陣為：

3）計算權重值

用判斷矩陣求權重的方法有很多種，包括和法、最小夾角法和特征向量法等，本文使用特征向量法。首先，計算判斷矩陣A 的最大特征值λmax；然后，根據式（6）求相應正特征向量（分量全大于0的特征向量）。

式中，λmax為矩陣A 的最大特征值，W 為其特征向量，將其進行歸一化處理，即得權重向量。

經計算，A 的最大特征值為λmax=4.043，權重向量為W（A）= （0.520，0.201，0.201，0.078）。

4）矩陣的一致性檢驗一致性檢驗的步驟：

①計算判斷矩陣的一致性指標

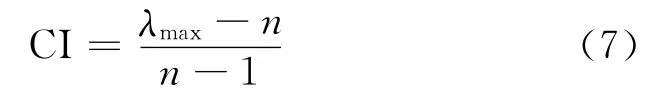
②從表2中查找平均隨機一致性指標RI

表2 平均隨機一致性指標Tab.2 Random index

③計算一致性比例CR

若CR＜0.1，認為A 具有滿意的一致性，接受A；否則，放棄A 或對A 的數據做適當調整。經檢驗得CR=0.016＜0.1，表明具有可接受的一致性。

5）計算合成權重

上述計算得到的只是準則層B 中各元素相對目標A 的權重向量，最終目的是要得到方案層C 中各元素對于目標A 的權重向量。因此，分別構造方案層對于準則層元素的判斷矩陣B1，B2，B3，B4，然后按上述方法計算權重向量得

則合成權重為：

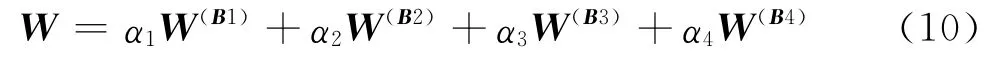
式（10）中，α1、α2、α3、α4分別為W（A）的四個分量，得W = （0.151，0.238，0.210，0.401）。經矩陣的一致性檢驗得CR=0.024＜0.1，由此說明合成權重具有良好的一致性。

6）確定二叉樹SVM 的結構

依據上述故障的權重值對故障類型進行排序，權重值大的類型優先診斷，保證將權重值大的類別首先識別出來。

改進算法將AHP和二叉樹SVM 結合起來，充分利用AHP的主觀優勢確定權重，為模型結構的建立提供依據。克服了AHP過分依賴專家主觀判斷的缺點，同時彌補了二叉樹SVM 不能反映決策者偏好的缺陷。兩種算法的結合能夠充分發揮各自的優勢，克服算法本身存在的缺陷。

3 仿真驗證

故障診斷過程主要包括故障特征提取和模式識別兩大步驟，利用小波包分解得各頻帶分量的能量，歸一化處理得到特征向量，將其作為SVM 的輸入進行故障模式識別。下面將改進算法用于發電機軸承的故障診斷，診斷模型如圖3所示。

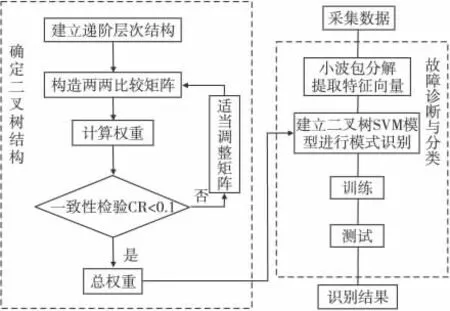
圖3 基于AHP和二叉樹SVM 的診斷模型Fig.3 Diagnosis model based on AHP and binary tree SVM

3.1 特征向量的提取

對于正常、外圈故障、內圈故障和滾珠故障4種狀態各提取50組樣本數據，其中40組用于訓練，另外10組用于測試。處理和提取故障特征向量的步驟如下：

1）本文實驗所用的實測軸承振動數據來自美國凱斯西儲大學的電氣工程實驗室［9］。如圖4 所示為一組不同故障狀態下的樣本圖。

2）采用db3小波對振動信號進行3層小波包分解，得到8個子頻帶的小波包分解系數。以一組外圈故障信號為例進行小波包分解，如圖5所示。

3）計算圖5中8個頻帶的能量值，進行歸一化處理得故障的特征向量如式（11）。

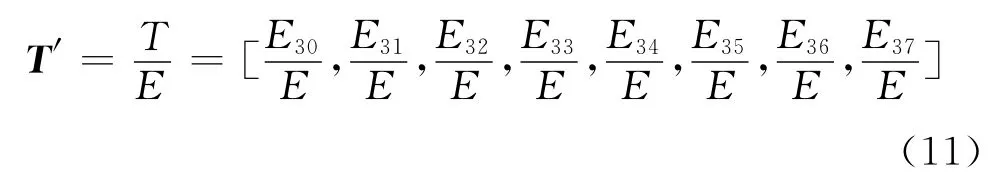
式（11）中，E3i（i=0，1，…，7）為各頻帶能量值，E 為能量總和。

4）重復上述步驟，提取多組特征向量。

3.2 多類分類器的構造

建立故障樣本集：（xi，yi），xi∈R8為樣本輸入，yi∈｛1，2，3，4｝為樣本輸出，代表四種故障類型，i=1，2，3，4。

由合成權重W = （0.151，0.238，0.210，0.401）判斷軸承故障診斷的順序為：滾珠故障、內圈故障、外圈故障、正常。所以二叉樹SVM 診斷結構如圖6所示。

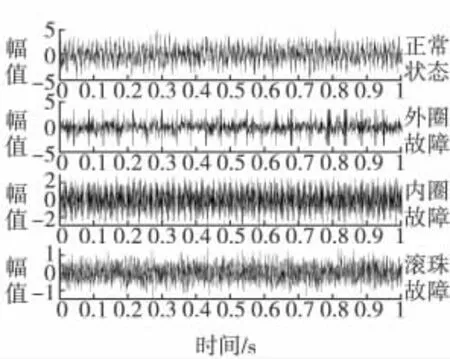
圖4 振動時域波形圖Fig.4 Vibration time-domain waveform

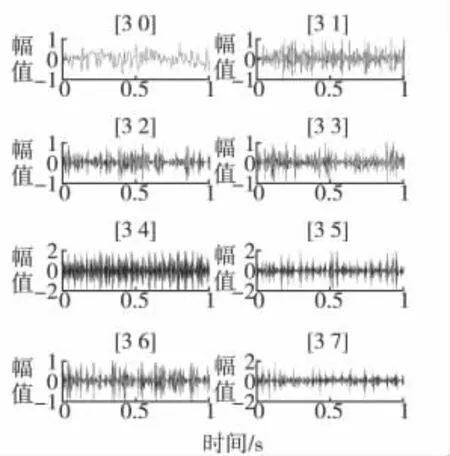
圖5 小波包分解圖Fig.5 Wavelet packet decomposition

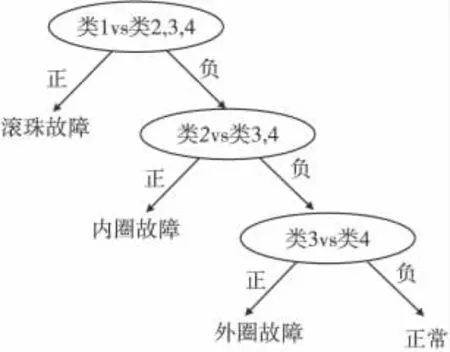
圖6 二叉樹SVM 診斷結構圖Fig.6 Diagnosis structure of binary tree SVM

3.3 故障模式識別

建立二叉樹SVM 的結構后，進行故障模式識別，步驟如下：

1）確定影響SVM 分類性能的參數。本文SVM 的核函數選取徑向基核函數（RBF）

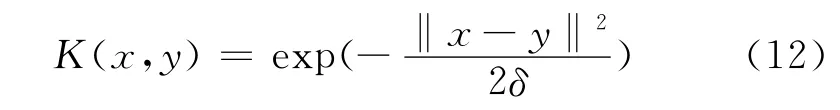
式（12）中，δ為核寬度。此外，需確定懲罰因子c。

參數δ和c 的選擇直接影響SVM 的分類精度和泛化能力。為確保快速有效地尋找最優參數（δ，c），采用遺傳算法尋優得到參數組合（4，224）。

2）輸入訓練樣本，完成訓練過程。

3）將測試樣本輸入訓練好的二叉樹SVM，檢驗識別能力。

4）在相同的樣本數據和參數設置的前提下，運用不同多分類算法進行故障診斷。

將各類算法進行故障診斷的結果進行統計，對比結果如表3所示。其中M1代表本文算法，M2與M3均代表二叉樹SVM 算法，M2算法中二叉樹的結構根據故障頻率設計，M3 算法中二叉樹的結構根據樣本分布范圍設計，M4代表一對多法，M5代表一對一法，M6代表決策導向無環圖法。

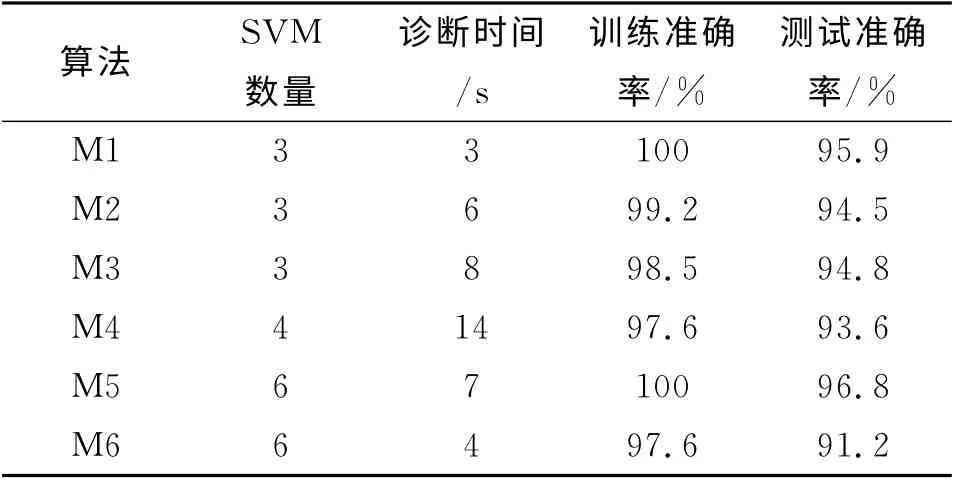
表3 不同多分類算法診斷結果統計Tab.3 Diagnosis statistics of different classification algorithms

通過表3中的對比數據可知，一對一法診斷準確率最高，達到96.8%，但耗時相對較長；其次為改進算法，診斷準確率為95.9%，同時改進算法診斷時間短，需要的SVM 數量少，這一點有利于SVM的推廣。與另外幾種算法作比較，改進算法無論在診斷準確率和診斷時間方面均占優勢。因此，綜合多個衡量指標，基于AHP和二叉樹SVM 的多故障分類算法優于其他幾種算法。

4 結論

本文提出了將AHP 和二叉樹SVM 相結合的多故障分類算法。該算法綜合考慮了影響分類精度的多個影響因子，運用層次分析法計算各類故障的權重，根據權重值設計了多類分類器的結構。仿真驗證表明，該算法適合進行多類故障診斷，相比較一對一法、一對多法等算法診斷效率更高，診斷精度更好，推廣應用前景較廣。

［1］統計學習理論的本質［M］.張學工，譯.北京：清華大學出版社，2000.

［2］胥永剛，孟志鵬，陸明.基于雙樹復小波包變換和SVM的滾動軸承故障診斷方法［J］.航空動力學報，2014，29（1）：67-73.

［3］W idodo A，Yang B S.Application of nonlinear feature extraction and support vector machines for fault diagnosis of induction motors［J］.Expert Systems with Applications，2007，33（1）：241-250.

［4］康守強，王玉靜，姜義成，等.基于超球球心間距多類支持向量機的滾動軸承故障分類［J］.中國電機工程學報，2014，34（14）：2319-2325.

［5］袁勝發，褚福磊.次序二叉樹支持向量機多類故障診斷算法研究［J］.振動與沖擊，2009，28（3）：51-54.

［6］趙海洋，徐敏強，王金東.改進二叉樹支持向量機及其故障診斷方法研究［J］.振動 工程學報，2013，26（5）：764-770.

［7］謝金明.水庫泥沙淤積管理評價研究［D］.北京：清華大學，2012.

［8］梁晨.子午線輪胎綜合接地性能評價體系與方法研究［D］.鎮江：江蘇大學，2013.

［9］The Case Western Reserve University Bearing Data Center Website.Bearing Data Center Seeded Fault Test Data［EB／OL］.［2007-11-27］.http：／／www／eecs／cwru／edu／laboratory／bearing／.