論高考改革下的數學創新試題

夏文濤+馬生蘭

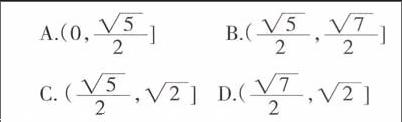
摘要：隨著課程改革的深入和我國高考改革的需要，新穎性、獨特性與探究性兼備的數學創新試題很可能會成為今后命題的一種趨勢和導向。探析高考數學創新試題的概念、特點和功能，有利于對其整體的理解和把握，對于搞好高中數學教學和高考數學備考復習是十分有益的。

關鍵詞：高考改革 高考數學 數學創新試題

隨著課程改革的深入和我國高考改革的需要，新穎性、獨特性與探究性兼備的數學創新試題很可能會成為今后命題的一種趨勢和導向。對于高考數學創新試題，學界至今還沒有明確定義，多數研究者就創新試題的背景、題型、編制、解答展開了一些研究，但是對創新試題的基本問題——概念、特點、功能基本沒有明確闡述，這對于進一步研究高考改革下的數學創新試題是不利的。筆者在對相關文獻研究的基礎上，通過對典型高考數學創新試題的分析與探究，試圖初步提出高考數學創新試題的概念、特點、功能。

一、高考數學創新試題的概念

羅增儒教授認為數學題是指數學上要求回答或者解釋的事情，需要研究或解決的矛盾[1]。這是目前對數學題廣為認可的一種定義，但是其外延尚顯廣泛。筆者認為，通常情況下，數學題是指在數學教學或數學學習中，基于診斷或測評目的，由數學教師或者教育研究者根據課程標準和命題理論設計、提供給學生解決的數學問題。

數學題的一般形式包含2個基本的部分：條件（已知，前提），結論（未知，要求）。條件一般具有一定的背景（題目背景），需要借助一定的數學語言（文字、符號、圖表）提供若干已知信息，結論一般指示求值、求證、判斷等。

目前，學界對創新試題還沒有統一的認識，基于文獻研究和對典型創新試題的探析，筆者認為高考數學創新試題是指根據數學課程標準的理念和要求，依托一定數學命題原理和技術，旨在培養、診斷、測評學生的創新意識與創新能力，在試題背景、試題形式，試題內容或解題方法等方面具有一定的新穎性與獨特性的數學題。

二、高考數學創新試題的基本特點

傳統的數學題具有接受性、封閉性和確定性等特征[2]。一般來說，數學題考查的內容應該是學生熟知的數學知識，學生通過對例題的程序式的模仿，可以順暢地完成對數學問題的解答。同時，它的形式結構一般是常規的，條件充分簡潔，設問清晰明確，答案唯一確定，學生可以利用所學的數學知識、方法去解決它。另外，它的考查目的在于鞏固學生的數學知識，培養學生的數學能力，一般具有一定的挑戰性。

除具有以上一般數學題的特點外，數學創新試題還有一些其他比較突出的特點。通過對最近10年來典型數學創新試題的分析和研究，筆者認為高考數學創新試題有以下的特點：

1.立意的鮮明性

立意是指試題的考查目的。高考數學試題的編制遵循“能力立意”的指導思想，這里的能力主要有空間想象能力、抽象概括能力、推理論證能力、運算求解能力、數據處理能力以及應用意識和創新意識等7大數學能力。數學創新試題立足學生的知識基礎，著力考查數學能力、數學素養，注重測量其發展性學力和創造性學力。因此，數學創新試題的立意重在檢測學生對基礎知識的掌握情況，考查數學思想方法，考查7大數學能力，特別是考查數學創新意識和創新能力。

2.背景的新穎性

試題的背景是指數學題中學生能夠理解的生活現實、數學現實以及其他學科現實。傳統意義上，數學試題多是以數學現實為背景。隨著素質教育的推進，特別是課程改革的深入發展，以數學現實為背景的數學試題不斷豐富，如高等數學背景、競賽數學背景、數學史背景等；以生活現實、其他學科現實為背景的數學題也逐漸增多，如生活情境問題、物理情境問題等。

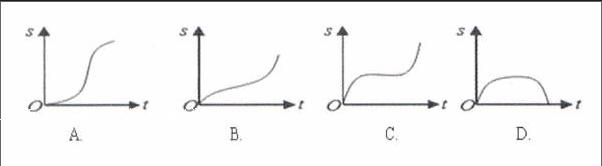
例1.（2008年全國I卷）汽車經過啟動、加速行駛、勻速行駛、減速行駛之后停車，若把這一過程中汽車的行駛路程看作時間的函數，其圖像可能是（ ）

本題以物理學位移與時間的關系為背景，也具有一定的現實生活背景，考查學生運用數學知識與方法解決問題的能力。此題讓學生感受到高考數學試題的學科綜合性，也體現了數學的廣泛應用性，又具有教導我們關注現實生活、學會應用數學的導向意義。

3.形式的靈活性

試題的形式包含數學試題的呈現方式、設問方式以及題型。目前，數學創新試題的呈現形式多樣，如采用文字、符號、圖形、圖表等呈現問題條件，學生需要通過閱讀、分析其中的數量關系或者圖形關系，推理、判斷或者探索其中的規律解決相關問題。開放題引起數學教育界的廣泛關注后，很多設問方式靈活多變的試題不斷出現，它們要求學生充分運用發散性思維，從多角度、多層次去分析和解決問題。另外，為了診斷、測評的需要，傳統的數學題型，如選擇題、填空題、解答題等，已經不能滿足當前課程改革中教育評價的要求，一些新的題型應時而出，如復合型選擇題、復合型填空題等。

例2.（2010年安微卷）若a>0，b>0，a+b=2，則下列不等式對一切滿足條件的恒成立的是______（寫出所有正確命題的編號）。

①ab≤1；②■+■≤■；③a2+b2≥3；

④a3+b3≥3；⑤■+■≥2。

例2為改良的客觀題型，需要多次判斷，才能做出正確的選擇，我們稱之為復合型填空題，它有利于綜合考查學生的能力，能夠比較理想地預防猜選。

4.內容的綜合性

試題的內容是指數學試題所包含的數學知識。課程改革以來，數學高考命題要求從學科的整體高度和思維價值的高度考慮問題，在知識網絡的交匯點處設計試題。數學試題包含多個知識點，不僅是數學知識密切關聯的內在要求，也是數學測試兼顧范圍和題量的必然選擇。因此，高考數學多數試題呈現出多個知識點交匯的特點，命題者精心挑選相互交匯的知識板塊，合理地控制數目和難度，最終能夠生成別出心裁的數學創新試題，全面考查學生知識掌握程度和問題解決能力。

例3.（2011年陜西卷）設集合M={y|y=|cos2x-in2x|，x∈R}，N={x||■|<1，x∈R}（i為虛數單位），則MIN為（ ）endprint

A.（0，1） B.（0，1] C.[0，1） D.[0，1]

本題綜合了三角函數、復數、集合等數學知識，設計簡潔、突出基礎、考查能力，特別是絕對值和復數模的考查，十分巧妙。

5.方法的多樣性

解題方法是指解決數學試題所用的一般解答方法和數學思想方法。很多數學創新試題都能一題多解，學生可以根據自己數學學習經驗，選擇不同的解答方法和思想方法作答。

例4.（2013年重慶卷）在平面上AB1⊥AB2，|OB1|=|OB2|=1，AP=AB1+AB2。若|OP|<■，則|OA|的取值范圍是（ ）

A.（0，■] B.（■，■]

C. （■，■] D.（■，■]

本題是向量的綜合應用問題，學生可以根據自己的知識結構，選擇不同的解題方法，如解析法、函數法、向量運算法等，至少有10種方法。

三、高考數學創新試題的功能

長期以來，在數學教學和數學學習中，數學解題是最常見的活動形式。它有利于學生對數學概念的理解，對數學基本知識的掌握，對數學思想方法的獲得，以及學生能力的發展，對全面提高學生的數學素養有重要的意義，因此，數學解題在數學教育教學中占有重要的地位，數學題對于數學教育教學具有重要的價值和功能。鑒于高考數學創新試題的概念和特點，除包含數學題一般功能外，它還具備鮮明的導向功能、測評功能和診斷功能。

1.導向功能

（1）數學創新試題是檢測學生能力和創新意識的現實需要

《普通高中數學課程標準（實驗）》（以下簡稱《高中課標》）[3]明確指出筆試仍是定量評價的重要方式，但要注重考察對數學概念的理解、數學思想方法的掌握、數學思考的深度、探索與創新的水平以及應用數學解決實際問題的能力等。

《2013年高考數學新課標考試大綱》規定創新意識是7大數學能力要求之一，創新意識是理性思維的高層次表現，也是發現問題和解決問題的重要途徑，有利于學生對所學的數學知識進行有效的遷移、融合，有利于學生未來的長遠發展。

因此，在筆試為主的考評體系下，考查學生的創新能力和創新意識，設置數學創新試題是現實的做法。

（2）數學創新試題是全面發展學生能力和創新意識的必要選擇

對于傳統的數學題，學生只要學好課本上的那些條條框框的知識，就能照搬課本的知識、方法輕而易舉做好它們。在此過程中，學生雖然鞏固了所學知識和方法，但是卻停留在簡單模仿、機械訓練的水平，其能力的發展很有限。

數學創新試題一般包含新穎的問題背景，具有靈活的問題形式和設問方式，綜合多個知識點、思想方法，設置發散性的解答方法。解答數學創新試題，不僅有利于學生鞏固所學知識，引導學生構建知識網絡和掌握數學思想方法，發展數學閱讀能力、分析和解決問題的能力，也有利于培養學生的數學興趣和愛好，全面提高學生數學素養。更重要的是，學生通過對數學知識進行有效地遷移、組合和融會，選擇數學思想方法創造性解決問題，對學生創新能力和意識的提高有重要意義。

2.測評功能

（1）數學創新試題有利于測評學生的創新能力和創新意識

數學創新試題一般具有新穎的問題背景和一定的深度、廣度，兼具多樣性、探究性，重點考查學生對數學知識的遷移、組合、融會的能力和分析、解決問題的能力，能夠比較理想地測評學生數學創新能力與意識。

（2）數學創新試題有利于更好地選拔優秀人才

由于數學創新試題背景新穎、內容豐富、形式靈活、方法多樣，因此它不僅能夠考查學生對數學基礎知識、基本技能的掌握情況，還能考查其對數學思想方法掌握情況，同時也能夠考查其繼續學習的潛能，拉開學生分數差距，進而為不同層次的高校提供不同水平的優秀人才。

3.診斷功能

（1）數學創新試題有利于教師提高教學質量

在課堂教學中，為了教學需要，教師必須要準備恰當、典型的數學題，去了解學生理解、掌握的情況，從而調控教學內容、進程。考慮到學生可能會提前預習，以及課本例題比較簡單，根據教學需要，教師可以合理地更改例題的背景、形式等，或者選擇一些典型的高考數學創新試題作為課堂講練的例題。這樣，教師可以根據學生的做題情況，盡可能全面了解學生的學習情況，準確評估教學效果，調控教學內容、進程，提高課堂教學質量。

（2）數學創新試題有利于學生提升學習水平

根據情況的不同，課后習題的布置各異。課后習題的選擇，既要綜合考慮學生課堂教學的情況、學生的實際水平，又要兼顧學優生、學差生，同時還要注意發展學生的數學能力和創新意識。由于數學創新試題具有一定的新穎性和探究性，因此，可以選擇或改編具有一定梯度、創新度的數學創新試題作為課后作業。教師通過作業情況進一步了解學生學習效果，引導學生加深對數學知識、思想方法的理解和掌握，幫助分析總結學習經驗教訓，指導學生做好學習、復習計劃，這樣有利于學生不斷提高學習水平。

————————

參考文獻

[1] 羅增儒.中學數學解題的理論與實踐.南寧：廣西教育出版社，2008.

[2] 張奠宙，宋乃慶.數學教育概論.北京：高等教育出版社，2009.

[3] 中華人民共和國教育部.普通高中數學課程標準（實驗）.北京：人民教育出版社，2003.

[作者：夏文濤（1984-），男，河南信陽人，重慶師范大學數學學院2012級在讀碩士；馬生蘭（1989-），女，青海互助人，重慶師范大學數學學院2013級在讀碩士。]

【責任編輯 任洪鉞】endprint