基于改進人工蜂群參數尋優的網絡行為分類

楊 宇， 毛 力 ， 王曉鋒， 周長喜

(江南大學 物聯網工程學院，江蘇 無錫214122)

隨著互聯網絡的發展，網絡規模的擴大，網絡中的各種不良行為對用戶的安全造成越來越多的威脅。面對網絡中的海量數據，網絡行為分類需要處理和重要信息同等數量甚至更多的數據，同時還要在不影響網絡性能的前提下實現實時監控。這就對系統的運算時間和運算空間提出來了更高的要求。Vapnik 提出的基于支持向量機(Support Vector Machine，SVM)的分類算法是對樣本數據進行預測和分類問題的一種有效方法，在網絡行為分類領域得到廣泛應用［1－3］。為了滿足實際應用的需要，在SVM 做分類識別時需要調節相關參數(主要是懲罰因子C 和核函數參數g)才能得到比較理想的預測分類準確率［4］。

近年來，在SVM 參數尋優領域出現了一種新型的全局隨機搜索方法——人工蜂群算法(Artificial Bee Colony，ABC)［4－6］。ABC 算法具有計算簡單、參數設置少的優點，因此與其他參數尋優算法(如粒子群算法、遺傳算法、蟻群算法)相比，具有比較明顯的優勢［4－6］。然而，傳統的ABC 算法在用于SVM算法參數尋優的過程中容易陷入局部最優解，無法達到最優分類效果［7］。很多學者對傳統ABC 算法做出了改進:王鑫等［8］通過自適應的位置更新、信息素與靈敏度配合選擇模型以及最差解替代等方法改進了傳統ABC 算法收斂速度慢和容易陷入局部最優的缺點;趙丹亞等［9］引入文化算法雙層進化結構和多種群并行進化思想，提出基于雙層進化的多種群并行人工蜂群算法以克服傳統ABC 算法容易陷入早熟收斂的不足;畢曉君［10］通過設計新的選擇策略和收斂策略，利用基于反向學習的變異策略代替偵查蜂的行為達到避免陷入局部最優的效果;王冰［11］和Anan B 等［12］采用基于當前局部最優解的搜索策略，加快了收斂速度;向萬里等［13］提出基于輪盤賭的反向選擇機制以保持蜂群個體的多樣性而使算法保持較好的進化能力;銀建霞等［14］、WU R 等［15］在傳統人工蜂群算法中跟隨蜂更新蜜源的階段，引入混沌序列更新蜜源，以提高跟隨蜂在此階段的局部搜索能力。

針對使用傳統參數尋優方法的SVM 算法識別網絡行為分類效率低和準確率不高的問題，文中提出了一種高效的基于人工蜂群參數尋優的網絡行為分類方法，即基于當前最優解的局部搜索策略并引入基于混沌序列的動態搜索因子改進傳統的人工蜂群算法(改進后的算法記作CABC)，尋找SVM最優參數，以達到快速準確進行網絡行為分類的目的。

1 基于人工蜂群的SVM 算法參數尋優

1.1 傳統SVM 及其尋優原理

支持向量機的基本思想是將非線性可分的樣本通過非線性變換映射到一個高維空間。在這個高維空間中，尋找一個最優分類超平面作為決策曲面，使得正類和反類之間的分類間隔最大。將SVM的學習過程轉化為優化問題，給定訓練樣本集(xi，yi)，i = 1，2，…，l，x ∈Rny ∈{± 1}，超平面記作ωTx + b = 0。尋找最優超平面即轉化為最小化公式

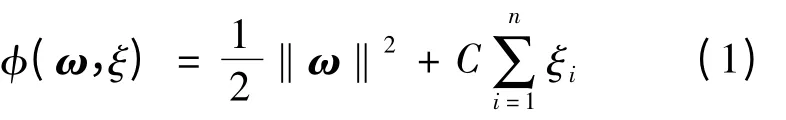
st

其中:ω 為超平面的法向量;C ＞0 為錯分樣本的懲罰因子;ξ 為松弛變量;b 為閾值，b ∈R。

引入Lagrange 函數，將二次規劃問題轉化為相應的對偶問題，即求解公式

其中，K(xi，xj)為核函數，其值受核函數參數g 的影響。文中選用的核函數為 RBF(Radial basis function，徑向基核函數)。

RBF 核函數是一個普遍適用的核函數，對參數敏感，通過參數選擇，可以適用于任意分布的樣本。它的一般表示為

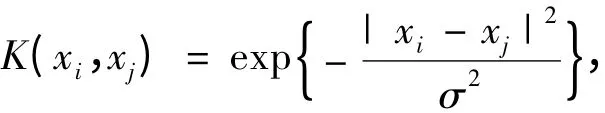
其中，σ(σ ＞0)為核函數的半徑。Vapnik 等在研究中發現，不同的核函數對SVM 性能的影響不大，核函數的參數g 和誤差懲罰因子C 是影響SVM 性能的關鍵因素［16］。

由此可見，問題的關鍵就是在最優核函數下尋找最優的懲罰因子C 和核函數參數g，從而使正確分類率最大［4］。傳統的SVM 參數尋優需要對參數C和g 在給定范圍內進行窮盡搜索，總的搜索時間為O(I × N)，I 為訓練樣本個數，N 為搜索次數［17］。對于小樣本數據而言，窮盡搜索的運行時間尚能夠接受，但是一旦數據規模增大，算法的運行時間將會呈幾何級數增長，故無法適用。所以文中使用改進的ABC 算法迅速準確地獲取優化參數C 和g，從而避免窮盡搜索耗費的巨大計算量。

1.2 人工蜂群算法原理

人工蜂群算法［18］通過模擬蜜蜂的采蜜機制求解函數優化問題，把每個蜜源視為問題的一個解，花蜜數量對應解的適應度值。將蜜蜂分為3 類:雇傭蜂(employed bees)、跟隨蜂(onlookers)和偵查蜂(scout bees)。為每個雇傭蜂初始化一個隨機的蜜源位置，雇傭蜂負責在各蜜源附近搜索新蜜源，根據前后蜜源的花蜜數量選擇較優蜜源并標記;跟隨蜂在以上部分較優蜜源附近作局部搜索，與標記蜜源進行比較，選取較優異的蜜源作為本次循環的最終標記蜜源;如果在局部搜索過程中，雇傭蜂標記的蜜源經過若干次搜索比較后仍不變，相應的雇傭蜂變成偵查蜂，隨機搜索新蜜源。每個雇傭蜂利用下式更新蜜源，即雇傭蜂更新蜜源

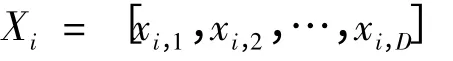
到新蜜源

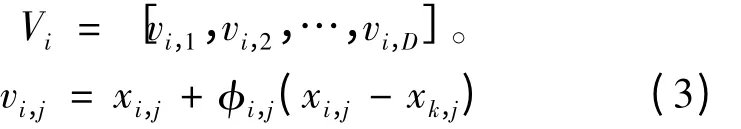
其中，xi，j和vi，j為個體Xi和個體Vi的第j 維分量;k ∈{1，2，…，NSN}，j ∈{1，2，…，D}，k 和j 都是隨機選擇的，且k ≠i，φi，j∈［－1，1］的隨機數，控制xi，j鄰域的生成范圍;NSN為蜜源的數量;D 為蜜源位置向量的維度。

跟隨蜂根據輪盤賭的方式選擇部分優質蜜源進行局部搜索，根據

計算每個蜜源被選擇的概率Pi。其中，NSN與雇傭蜂或跟隨蜂數量的值相等;fiti為第i 個蜜源的適應度值。由于優化SVM 的主要目的在于獲得更高的分類正確率，而SVM 算法在使用交叉驗證時，svmtrain 的返回值是交叉驗證下的平均分類準確率，記作fi，所以fiti可由下式得到。

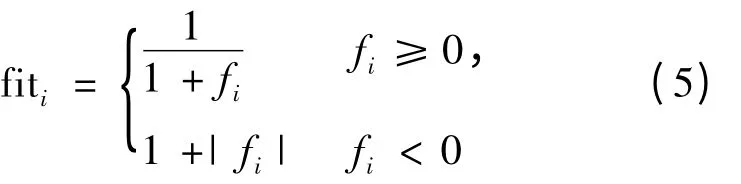
跟隨蜂在每個被選中的蜜源鄰域按照式(3)進行局部搜索產生新的蜜源。如果新的蜜源優于舊的蜜源則替換，否則保留。

若蜜源經過limit 次循環沒有被更新，則偵查蜂通過下式

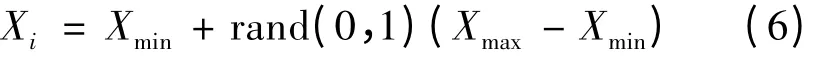
隨機搜索新蜜源。其中，Xmax和Xmin為解空間的上、下邊界。

1.3 基于當前最優解和混沌序列的局部搜索策略

ABC 算法中雇傭蜂和跟隨蜂執行相同的搜索策略。在式(3)和式(6)中，xk，j是隨機選擇的任一個體的一維分量，rand(0，1)和φi，j也是隨機數。這樣的隨機性導致搜索效率下降，尤其在訓練數據集較大和樣本屬性較多時，算法的尋優精度和收斂速度都會受到很大的影響。蜂群可以根據蜜源的位置信息比較蜜源的優劣，選擇當前最優蜜源并在其周圍進一步進行尋優，以此達到加快收斂速度的目的。

同時，利用混沌序列具有隨機、遍歷、非周期、不收斂的特性，引入混沌序列算子作為動態收縮因子的組成部分，與參數α 共同控制新解的搜索范圍。設

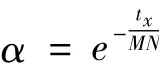
其中，tx為當前迭代次數。α 的值可以適時調節步長，有助于雇傭蜂和跟隨蜂尋找新蜜源，提高尋優性能。在迭代初期，由于新解的調整值較大，可有效擴大搜索范圍、確保種群的多樣性，提高算法跳出局部極值的能力，防止早熟收斂現象的產生;隨著迭代次數的增加，α 變小，新解的調整部分逐漸變小，有助于算法進行深度尋優并能快速尋找到最優解。根據Logistic 方程

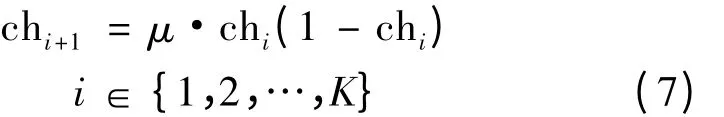
生成混沌序列。式中:混沌狀態控制參數μ 取4，使Logistic 方程完全進入混沌狀態;chi為屬于［0，1］的均勻分布的隨機數，且chi≠0.25，0.5 和0.75;K為混沌序列的長度。

雇傭蜂和跟隨蜂每次迭代更新蜜源時，通過下式

采用基于當前最優解的局部搜索策略并引入基于混沌序列的動態搜索因子，逐維更新蜜源每一維度的值，以增加可行解在搜索空間中的多樣性。其中:vi，j為新產生的蜜源Vi的第j 維分量;xi，j為上一個被搜索的蜜源Xi的第j 維分量;xb，j為當前最優解Xb的第j 維分量;j，k 均隨機選擇，且k ≠b，用于將當前最優解引入蜜蜂更新蜜源的公式;通過φi，j引入混沌搜索因子chi和參數α，控制xi，j鄰域的生成范圍。

1.4 算法流程

改進后的人工蜂群算法實現的具體步驟如下:

1)初始化算法參數:混沌序列長度K，最大迭代次數Nmax，判斷蜜源更新是否陷入停滯的控制參數limit;

2)隨機產生NSN個D 維解，作為初始種群，初始化迭代次數t = 0;雇傭蜂對每個蜜源Xi使用式(8)在它的鄰域附近逐維進行變異和更新。

3)計算鄰域內搜索到的每個蜜源Xi的適應度函數值fiti和選擇概率Pi。

4)跟隨蜂根據概率Pi選擇部分適應度較好的蜜源，然后每個跟隨蜂再根據式(8)在它的鄰域附近進行逐維局部搜索，并記錄其未更新次數。

5)判斷是否存在連續limit 次都未被更新的蜜源，若存在則由偵查蜂通過式(6)隨機搜索新蜜源。

6)記錄到目前為止的最優解。

7)判斷是否達到最大迭代次數MN，若滿足，則輸出最優解，否則轉到2)。

1.5 算法的時間復雜度分析

2 仿真實驗

2.1 實驗測試函數和對比算法

文中將CABC 算法與標準ABC 算法和文獻［12］中BSABC 進行比較以評估CABC 算法的魯棒性、尋優精度和收斂速度。

為了分析CABC 算法的性能，文中選定4 個經典測試函數對其進行測試，測試函數的定義、搜索區間和理論最優值見表1。其中，Step 是單峰函數，在定義域內只有一個最優解，用來測試算法的尋優精度和收斂速度;Griewank 函數和Rastrigin 函數是

ABC 算法的時間復雜度為O(MN × SN)［19］，文獻［12］中的Best－so－far ABC(以下簡稱BSABC)算法的時間復雜度也為O(MN × SN)。文中提出的CABC 算法對雇傭蜂和跟隨蜂的局部搜索策略進行了改進，ABC 算法中的兩種蜜蜂只是隨機選擇任意一維分量進行變異，而CABC 算法中的雇傭蜂和跟隨蜂則是在當前最優解的周圍逐維進行局部搜索，故其時間復雜度增加了O(MN ×SN ×(D －1))，其中D 為個體的維數。而在搜索時加入的混沌算子是一個長為K 的序列，所以對算法的時間復雜度沒有影響。CABC 算法的時間復雜度為O(MN × SN +MN × SN ×(D － 1))，故經過約減后CABC 算法的時間復雜度也為O(MN×SN)，即這3 種算法的時間復雜度相同。多峰函數，具有多個分布均勻的最優解，但Griewank 函數的局部最優解隨著維度的增加而增加，用于測試算法全局尋優的性能和避免早熟的能力;Rosenbrock 函數的全局最優解分布在一個又長又窄的拋物線形的平坦的山谷里，很難收斂到全局最優解，通常用以評價優化算法的性能［20］。

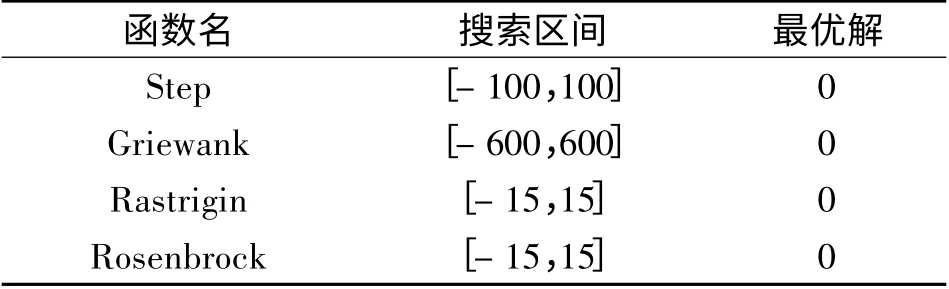
表1 測試函數Tab.1 Test function

表1 中，Step 函數表示為i=1

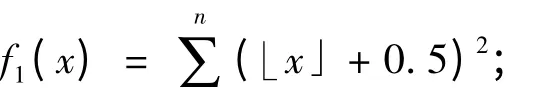
Griewank 函數表達式

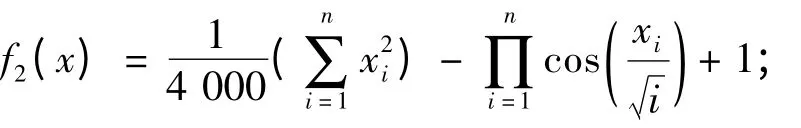
Rastrigin 函數表達式

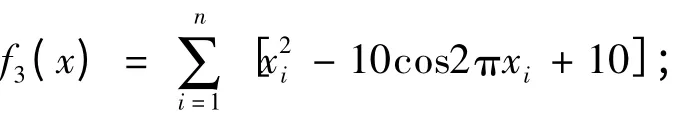
Rosenbrock 函數表達式

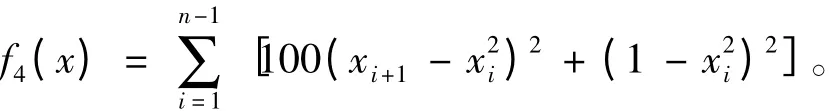
2.2 實驗結果分析

對比實驗的參數設置如下:最大迭代次數Nmax為1 000，控制參數limit 為50，初始化蜜源的數量NSN為50，維度D 為30。

3 種算法分別對4 個測試函數獨立運行30 次的測試結果見表2。

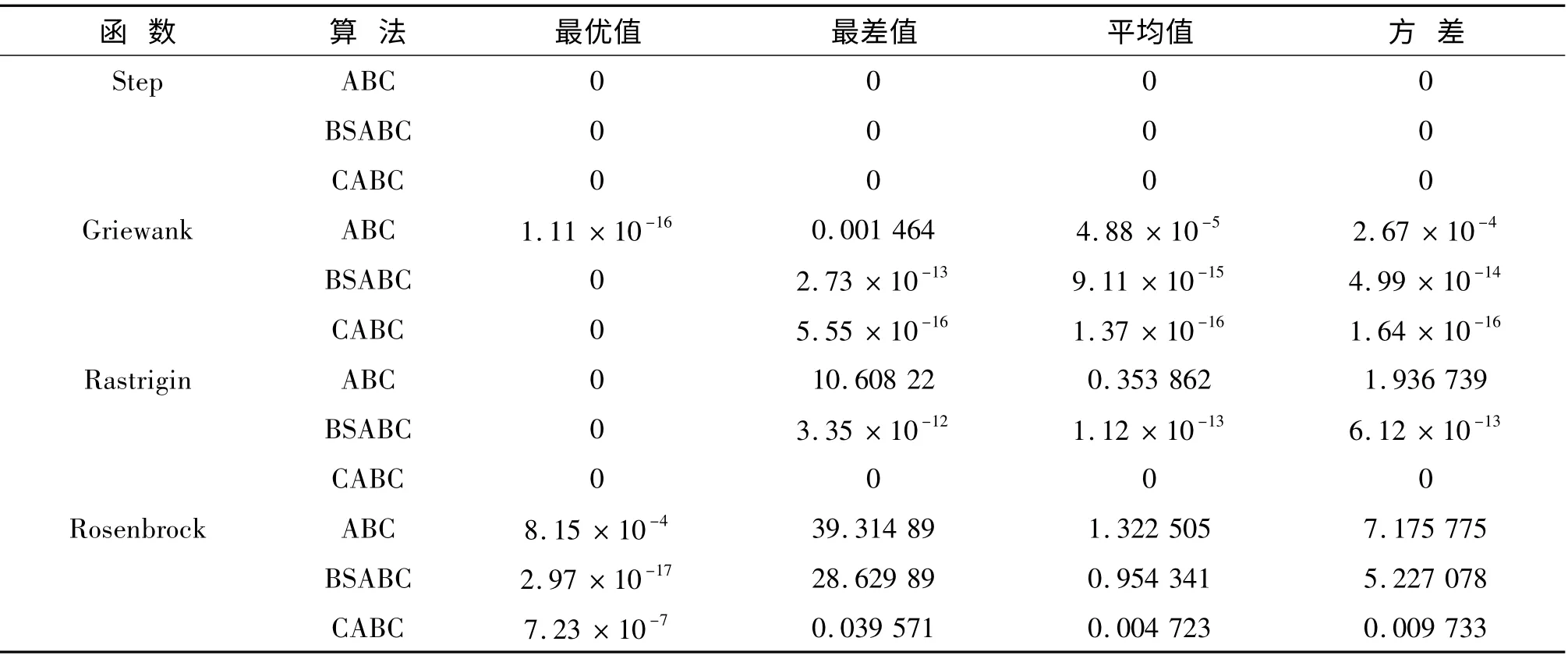
表2 30 維函數測試結果比較Tab.2 Comparison of the 30-dimensional function test results

表3 反映了在表2 實驗條件下，3 種算法運行時間的對比情況，平均運行時間即為不同算法分別對不同測試函數在各自獨立運行30 次時，達到收斂穩定精度所需要時間的平均值。圖1 ～圖4 分別給出了3 種算法對測試函數在各自獨立運行30 次時的平均適應值的進化曲線。

表3 30 維函數達到穩定精度的運行時間Tab.3 Runtime of the 30-dimensional function to stable precision

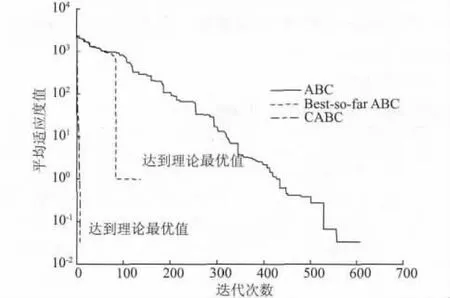
圖1 Step 在ABC，BSABC 和CABC 算法下進化曲線Fig.1 Evolution curves of ABC，BSABC and CABC by Step function

圖2 Griewank 在ABC，BSABC 和CABC 算法下進化曲線Fig.2 Evolution curces of ABC，BSABC and CABC by Griewank function

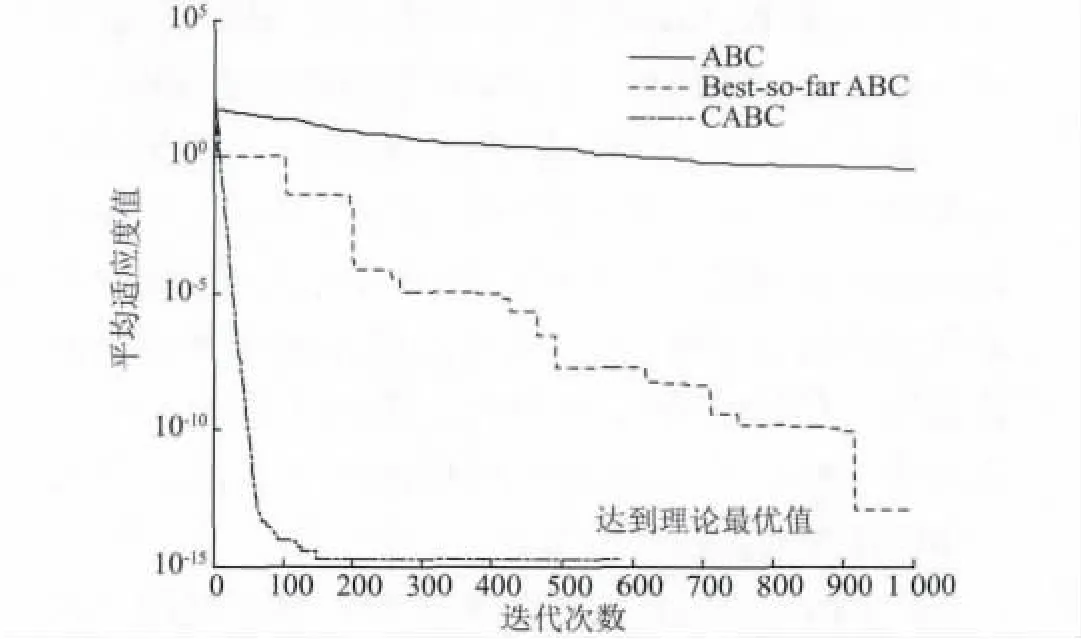
圖3 Rastrigin 在ABC，BSABC 和CABC 算法下進化曲線Fig.3 Evolution curves of ABC，BSABC and CABC by Rastrigin function

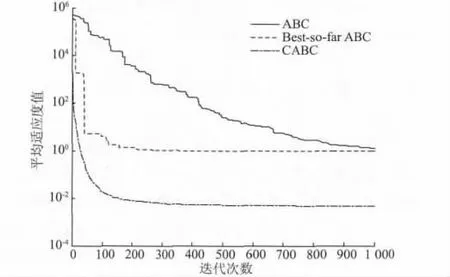
圖4 Rosenbrock 在ABC，BSABC 和CABC 算法下的進化曲線Fig.4 Evolution curves of ABC，BSABC and CABC by Rosenbrock function

由表2 中的數據可以看出，CABC 算法在4 種測試函數上的最優值和最差值的精度與標準ABC 算法和BSABC 算法相比都有明顯的提高。而且，由圖1可知，盡管在3 種算法下Step 函數都達到了理論最優值，但CABC 算法所需的迭代次數明顯小于標準ABC 算法和BSABC 算法。由圖2 和圖3 可知，CABC算法在Griewank 和Rastrigin 函數上均在200 次迭代內就達到了穩定精度，尤其是Rastrigin 函數，CABC算法可以快速的收斂到理論最優值0，與ABC 算法和BSABC 算法完成1 000 次迭代后仍不穩定相比明顯更優。

另外，由表3 可知，CABC 算法的平均運行時間明顯小于ABC 算法和BSABC 算法。雖然CABC 算法的每次迭代中在雇傭蜂和跟隨蜂搜索階段引入了混沌序列，嘗試均勻地向各個方向游動增加了計算量，從而增加了每次迭代的運行時間;但是從圖1 ～圖4 可以看出，CABC 算法達到穩定收斂精度所需要的迭代次數遠小于ABC 算法和BSABC 算法。顯然，從總體上來看，CABC 算法表現出比ABC 算法和BSABC 算法更高的收斂精度和更快的收斂速度。

表2 中顯示，CABC 算法的均值和方差都優于另外兩種算法，而且存在數量級級別的提升。尤其是Rosenbrock 函數，與BSABC 算法結果相比，雖然在最優值精度上稍差，但是就平均值體現的魯棒性而言仍然明顯優于BSABC 算法的優化結果。而圖1 ～圖4 中CABC 算法在迭代后期曲線的平滑更說明CABC 算法的魯棒性較高。

4 個函數的仿真結果表明，CABC 算法利用當前最優解和具有混沌特性的動態收縮因子改進了雇傭蜂和跟隨蜂的局部搜索方式，從而增強了該算法的局部搜索能力，顯著提高了最優解的精度;同時使算法的魯棒性和收斂速度得到明顯提高，在一定程度上防止了算法的早熟收斂。

3 CABC 參數尋優的網絡行為分類

為了證明算法的有效性，文中在Matlab 環境下用真實的網絡數據進行實驗。采用的KDDCUP99 數據集是MIT 林肯實驗室模擬美國空軍局域網網絡環境并從中采集的網絡連接數據和系統審計數據。其中，測試數據集和訓練數據集有不同的概率分布，使得網絡行為分類實驗更具有現實性。

實驗以訓練數據集中的部分記錄作訓練集，測試數據集中的部分記錄作測試集，取得C 和g 最優值后用 KDDCUP99 數據集的其他數據(Dataset1－Dataset4)評估CABC 算法在網絡行為分類方面的應用效果。實驗參數設置如下:最大迭代次數MN 為30，控制參數limit 為5，初始化蜜源的數量為10。

分別把兩種算法得到的最優參數和Libsvm 默認參數(C 默認1，g 默認為屬性數目的倒數)運用在其他4 組同源的訓練和測試數據集上，訓練和測試數據集都分別包含30 000 條記錄，運行結果比較見表4。

由表4 可以看出，在預測準確性基本一致的前提下，經過CABC 算法參數尋優后再進行檢測，模型的訓練時間和應用模型的檢測時間都有大幅度提高，僅為原來默認參數下的11% ～35%，為標準ABC 算法的20% ～50%。由此表明，CABC－SVM 可以成功應用到網絡行為分類領域，并且比ABC－SVM和默認參數的SVM 更快地取得分類結果，識別率穩定，可靠性好。

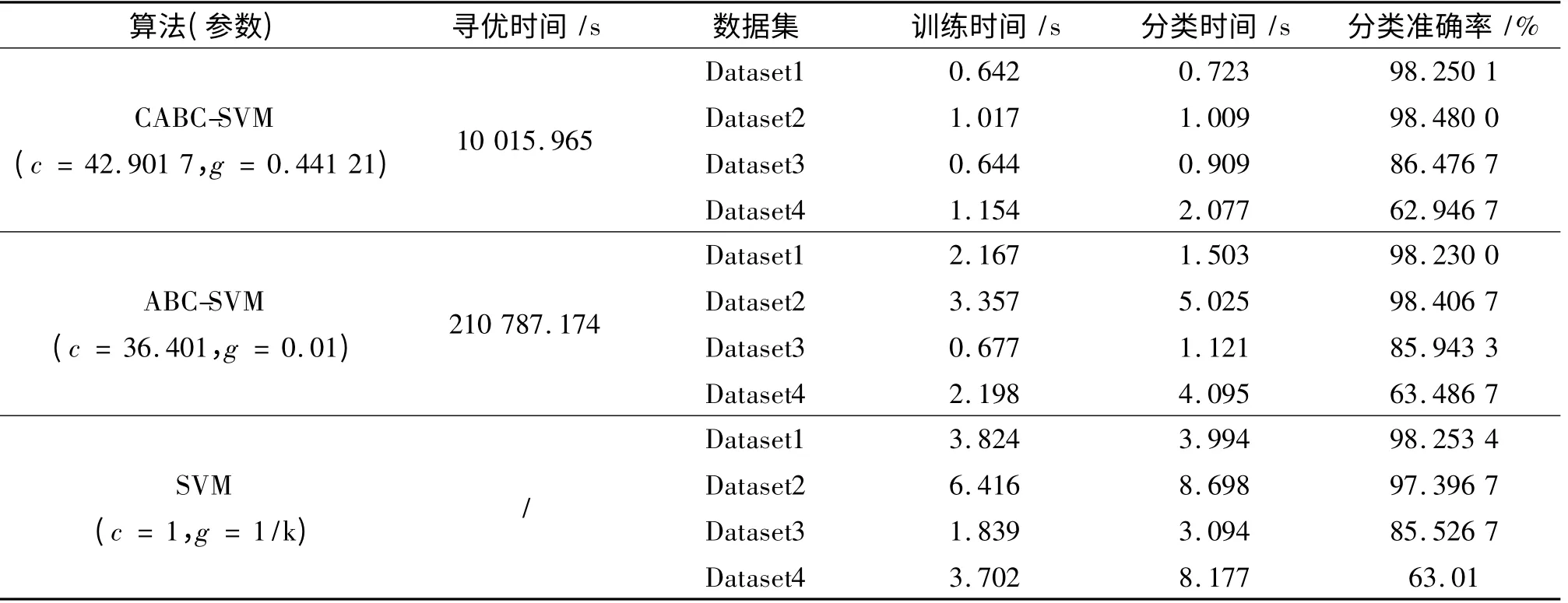
表4 3 種參數下的分類效果比較Tab.4 Comparison of the classification results under three kinds of parameters

4 結 語

文中在深入分析算法的基礎上，基于當前最優解和混沌序列，提出了具體的改進方案以克服標準ABC 算法的缺陷。基于經典測試函數的仿真結果表明，在求解函數最優解優化問題上，文中給出的CABC 算法具有較強的魯棒性，能有效避免算法陷入局部最優，并具有更高的尋優精度和更快的收斂速度。將改進的算法用于網絡行為分類領域，通過與ABC－SVM 算法和默認參數的SVM 算法的對比，實驗證明CABC 算法在具體應用上能夠取得更為理想的效果。

［1］熊剛，孟姣，曹自剛，等.網絡流量分類研究進展與展望［J］.集成技術，2012，1(1):32－42.

XIONG Gang，MENG Jiao，CAO Zigang，et al. Research progress and prospects of network traffic classification［J］. Journal of Integration Technology，2012，1(1):32－42.(in Chinese)

［2］王濤，余順爭.基于機器學習的網絡流量分類研究進展［J］.小型微型計算機系統，2012，33(5):1034－1040.

WANG Tao，YU Shunzheng.Advances in machine learning based network traffic classification［J］.Journal of Chinese Computer Systems，2012，33(5):1034－1040.(in Chinese)

［3］顧成杰，張順頤.基于改進SVM 的網絡流量分類方法研究［J］.儀器儀表學報，2011，32(7):1507－1513.

GU Chengjie，ZHANG Shunyi. Network traffic classification based on improved support vector machine［J］. Chinese Journal of Scientific Instrument，2011，32(7):1507－1513.(in Chinese)

［4］于明，艾月喬.基于人工蜂群算法的支持向量機參數優化及應用［J］.光電子·激光，2012，23(2):374－378.

YU Ming，AI Yueqiao. SVM parameter optimization and application based on artificial bee colony algorithm［J］. Journal of Optoelectronics·Laser，2012，23(2):374－378.(in Chinese)

［5］Mandal S K，Chan T S，Tiwari M K.Leak detection of pipeline:an integrated approach of rough set theory and artificial bee colony trained SVM［J］.Expert Systems with Applications，2012，39 (3):3071－3080.

［6］劉路，王太勇.基于人工蜂群算法的支持向量機優化［J］.天津大學學報，2011，44(9):803－805.

LIU Lu，WANG Taiyong. Support vector machine optimization based on artificial bee colony algorithm［J］. Journal of Tianjin University，2011，44(9):803－805.(in Chinese)

［7］GAO W，LIU S. Improved artificial bee colony algorithm for global optimization［J］. Information Processing Letters，2011，111(17):871－882.

［8］王鑫，譚華忠，蔣華.基于改進人工蜂群算法的視頻水印［J］.計算機工程與設計，2014，35(6):2095－2099.

WANG Xin，TAN Huazhong，JIANG Hua. Video watermark scheme based on improved artificial bee colony algorithm［J］.Computer Engineering and Design，2014，35(6):2095－2099.(in Chinese)

［9］趙丹亞，張月.基于雙層進化的多種群并行人工蜂群算法［J］.計算機工程與設計，2015，36(1):178－183.

ZHAO Danya，ZHANG Yue. Parallel evolution with multi－populations artificial bee colony algorithm based on dual evolution structure［J］.Computer Engineering and Design，2015，36(1):178－183.(in Chinese)

［10］畢曉君，王艷嬌.加速收斂的人工蜂群算法［J］.系統工程與電子技術，2011，33(12):2755－2761.

BI Xiaojun，WANG Yanjiao. Artificial bee colony algorithm with fast convergence［J］. Systems Engineering and Electronics，2011，33(12):2755－2761.(in Chinese)

［11］王冰.基于局部最優解的改進人工蜂群算法［J］.計算機應用研究，2014，31(4):1023－1026.

WANG Bing.Improved artificial bee colony algorithm based on local best solution［J］.Application Research of Computers，2014，31(4):1023－1026.(in Chinese)

［12］Anan B，Tiranee A，Booncharoen S.The best－so－far selection in artificial bee colony algorithm［J］.Applied Soft Computing，2011，11(2):2888－2901.

［13］向萬里，馬壽峰.基于輪盤賭反向選擇機制的蜂群優化算法［J］.計算機應用研究，2013，30(1):86－89.

XIANG Wanli，MA Shoufeng.Artificial bee colony based on reverse selection of roulette［J］.Application Research of Computers，2013，30(1):86－89.(in Chinese)

［14］銀建霞，孟紅云.具有混沌差分進化搜索的人工蜂群算法［J］.計算機工程與應用，2011，47(29):27－30.

YIN Jianxia，MENG Hongyun.Artificial bee colony algorithm with chaotic differential evolution search［J］.Computer Engineering and Applications，2011，47(29):27－30.(in Chinese)

［15］WU B，FAN S H.Improved Artificial Bee Colony Algorithm with Chaos［M］.Berlin:Springer，2011:51－56.

［16］John Shawe－Taylor，Nello Cristianini.模式分析的核方法［M］.趙玲玲，翁蘇明，曾華軍，等譯.北京:機械工業出版社，2006.

［17］龔永罡，湯世平.面向大數據的SVM 參數尋優方法［J］.計算機仿真，2010，27(9):204－207.

GONG Yonggang，TANG Shiping.A novel parameters optimization of SVM for large data sets［J］.Computer Simulation，2010，27(9):204－207.(in Chinese)

［18］GAO Weifeng，LIU Sanyang，HUANG Lingling.A global bvest artificial bee colony algorithm for global optimization［J］.Journal of Computational and Applied Mathematics，2012，236 (11):2741－2753.

［19］王翔，李志勇，許國藝，等.基于混沌局部搜索算子的人工蜂群算法［J］.計算機應用，2012，32(4):1033－1036.WANG Xiang，LI Zhiyong，XU Guoyi，et al.Artificial bee colony algorithm based on chaos local search operator［J］. Journal of Computer Applications，2012，32(4):1033－1036.(in Chinese)

［20］Ratnaweera A，Halgamuge S，Watson H C. Self－organizing hierarchical particle swarm optimizer with time－varying acceleration coefficients［J］.IEEE Transactions on Evolutionary Computation，2004，8(3):240－255.