冗余驅動消除Stewart 并聯(lián)機器人奇異位形

李保坤， 郭永存， 韓迎鴿， 曹 毅

(1.安徽理工大學 機械工程學院，安徽 淮南232001;2. 安徽理工大學 機械工程博士后流動站，安徽 淮南232001;3.安徽理工大學 電氣與信息工程學院，安徽 淮南232001;4. 江南大學 機械工程學院，江蘇 無錫214122)

六自由度Stewart 并聯(lián)機器人機構由于剛度大、承載能力強以及運動精度高等特點，已被廣泛應用于運動模擬器、醫(yī)療器械、工業(yè)機器人、微納操作、力/ 力矩傳感器、空間探測、并聯(lián)機床等多個高精技術領域［1］。然而，在該機構的位形空間內(nèi)存在大量復雜的奇異位形，機構在奇異位形附近工作時，運動學及靜力學性能將會變差;另外，由于奇異位形的存在，機構的有效工作空間將進一步縮小。為進一步提高并聯(lián)機器人機構的各項性能，應盡可能避開奇異位形或消除奇異位形對機構的不良影響。Nakamura Y 等［2］和Chiaverini S 等［3］從消除奇異位形對運動精度、笛卡爾剛度以及機構的動力學性能等方面進行了研究;基于反螺旋理論，郭盛等［4］提出了一種構造可避免任何可能的運動平臺奇異的三自由度轉動并聯(lián)機構的設計方法;張彥斌［5］通過構建雅可比矩陣，利用螺旋理論，按照支路分支連接度的不同綜合出具有無奇異的完全各向同性純移動并聯(lián)機構;張耀軍等［6］利用Grassmann 線幾何判定繩牽引平面并聯(lián)機構的奇異位形，并討論了該機構避免奇異位形的幾何條件;王玉新等［7］通過研究并聯(lián)機構構型分岔特性，提出了一種利用擾動函數(shù)規(guī)避并聯(lián)機構轉向點奇異的方法。比較常用規(guī)避奇異的有效方法通常是利用路徑規(guī)劃避免奇異位形，即基于任務空間計算出預期的運動軌跡，對其整個工作過程實施無奇異的路徑規(guī)劃，以保證機器人在整個任務操作過程中，機構不會出現(xiàn)奇異位形。基于運動規(guī)劃方法的奇異位形規(guī)避需要掌握機構奇異軌跡在機構位形空間內(nèi)的分布情況，對于六自由度Stewart 并聯(lián)機構，由于其位于位形空間內(nèi)的奇異位形分布極其復雜［8-9］，比較難以利用運動規(guī)劃法規(guī)避奇異位形。

文獻［10-13］提出可采用冗余驅動的方法消除奇異位形的影響，該方法通過添加適當?shù)娜哂囹寗右韵龣C構的所有存在的奇異點，方法實用有效。為消除奇異位對Stewart 并聯(lián)機器人機構的不良影響，文中主要闡述利用冗余驅動消除Stewart 并聯(lián)機器人機構的奇異位形的原理和方法，并以實例證明該方法的有效性。

1 冗余驅動的含義

冗余驅動并聯(lián)機器人機構一般具有兩種方式:①在保證機構自由度不變的前提下直接在原來并聯(lián)機構的基礎上增加驅動關節(jié)，這種方式比較簡單，但是增加了機構的不對稱性，影響機構的動力學性能，并且機構的運動學反解與正解會變的比較復雜。②增加一條與機構的支鏈完全相同的支鏈，并保證機構的自由度不變，然后在增加的支鏈中引入驅動關節(jié)，構成冗余驅動并聯(lián)機構。第②種方式可以非常容易地將驅動器安裝在基座上，保證機構的對稱性，并能使得機構的運動學反解簡單。

2 雅可比矩陣與奇異位形

未添加冗余驅動的六自由度Stewart 并聯(lián)機器人的結構如圖1 所示。

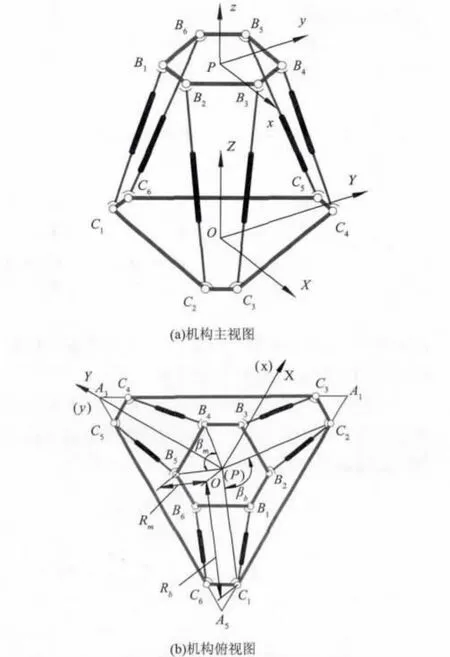
圖1 Stewart 并聯(lián)機器人的結構框架Fig.1 Schematic of the Stewart parallel manipulator

由圖1 可以看出，其動定平臺為兩個非相似型的半規(guī)則正六邊形B1B2…B6，C1C2…C6(i = 1，2，…，6)，并通過6 根相同的球副-移動副-球副(或萬向鉸)支鏈(BiCi)相連。Bi和Ci分別為動定平臺的6 個頂點，Aj(j = 1，3，5)為定平臺六邊形長邊的交點。其中:P 為機構動平臺幾何中心點;O 為機構定平臺幾何中心點;βm為動平臺上邊B4B5對應中心角，0° ≤βm≤120°;βb為定平臺上邊C1C2對應中心角，0° ≤βb≤120°。Rm為動平臺外接圓半徑;Rb為定平臺外接圓半徑。

為分析機構的奇異位形(見圖1)，在動、定平臺上分別建立動坐標系P-xyz 和固定坐標系O-XYZ。動平臺中心點P 在固定坐標系中的位置矢量記為P，動平臺上各個頂點Bi在固定坐標系中的位置矢量記為Bi(i = 1，2，…，6)，在動坐標系中的位置矢量記為bi(i = 1，2，…，6)，定平臺各頂點Ci在固定坐標系中的位置矢量記為Ci(i = 1，2，…，6)。

根據(jù)剛體位姿變換關系不難得到

其中，R 為動平臺的姿態(tài)。方程兩邊同時減去Ci，即可得到第i 根支鏈矢量表達式

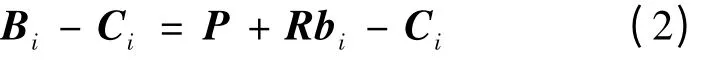
若將第i 根支鏈桿長記為li，則有

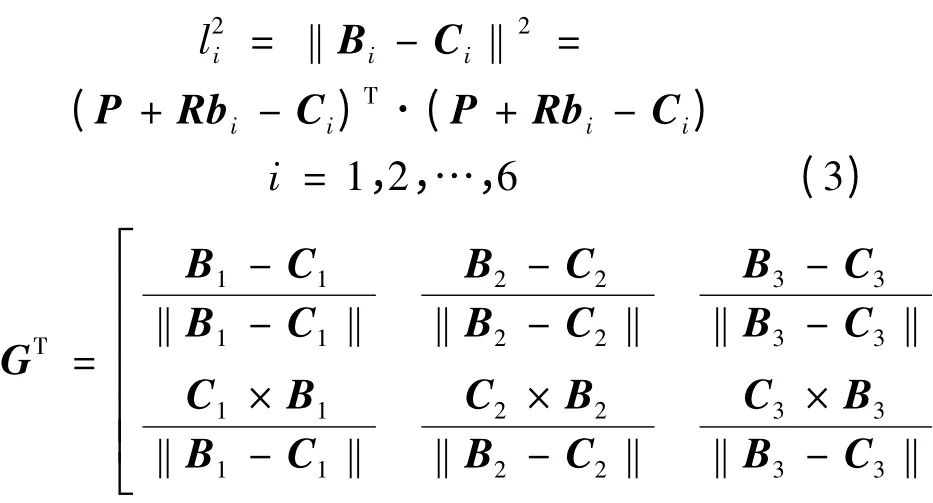
稱矩陣G 為由運動輸出到輸入的逆速度雅可比矩陣，矩陣GT為矩陣G 的轉置矩陣。

若增加一條與機構的支鏈完全相同的支鏈構建冗余驅動，則Stewart 并聯(lián)機構在速度空間上描述的由運動輸出到輸入的逆速度雅可比矩陣為

又由文獻［12］可知，Stewart 并聯(lián)機器人的逆速度雅可比矩陣G 的轉置矩陣GT也可表示為由關節(jié)力到操作力的線性映射，稱為力雅可比矩陣GFf，即有= GT。因而，映射后的矢量長度極值可以從度量特征上評價機構的運動學和靜力學性能。這些極值通常被定義為矩陣的奇異值

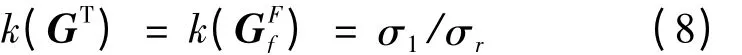
其中，σ1、σr分別為對應矩陣的最大奇異值與最小奇異值。當k =1 時，機構處于最佳的運動傳遞性能，稱機器人機構的這一形位為各向同性。一般在機器人的機構設計時，應盡量使其條件數(shù)取較小值，從而使機器人靈巧性較高。當矩陣的條件數(shù)是無窮大即k(GT)= ∞時，機器人處于奇異位形。

若機構處于某一奇異位形時，相應的逆速度雅可比矩陣至少存在一個奇異值為0，換言之，有限的關節(jié)速度將導致操作器速度趨于無窮大。為此，通常把至少有一個奇異值為0 時的雅可比矩陣對應的式(2)兩端對時間同時求一階導數(shù)，便可得到機構基于雅可比矩陣的輸入-輸出運動學方程

機構的輸出到輸入的逆速度雅可比矩陣可以表示為

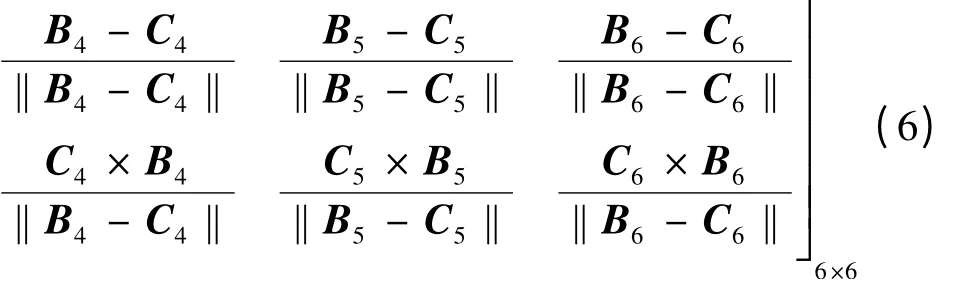
位形稱為奇異位形，此時雅可比矩陣的條件數(shù)是趨于無窮大的，在物理意義上可解釋為末端執(zhí)行器增加了至少一個不可控的自由度［1］。

當逆速度雅可比矩陣和力雅可比矩陣至少有一個奇異值為0 時，則均為欠秩矩陣。當矩陣GFf 的奇異值均大于0 時，則為是滿秩矩陣，即

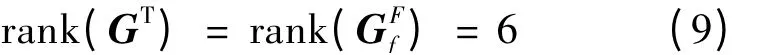
綜上所述，對于Stewart 并聯(lián)機構，無論是否為冗余驅動，均可通過判斷逆速度雅可比矩陣的轉置矩陣GT或力雅可比矩陣GFf 是否滿秩判斷是否處于奇異位形狀態(tài)。當它們滿秩時，機構不處于奇異位形;反之，則機構處于奇異位形。

3 冗余驅動消除奇異位形的方法

當Stewart 并聯(lián)機構處于奇異位形時，由于6 個約束力線性相關，機構的動平臺存在至少一個未被約束的剩余的瞬時自由度，機構不能保持靜力學平衡，機構受力狀態(tài)顯著變壞。為了與動平臺上很小的外力平衡，理論上需要非常大的驅動力，很容易損壞機構［1］。因此，必須避免奇異位形的產(chǎn)生。

以上分析可以看出，通過構造冗余驅動，使矩陣G 滿足式(9)，即可消除機構的奇異位形。

3.1 冗余驅動時的逆速度雅可比矩陣

當機構處于奇異位形時，rank(GT)= 6 －ε，添加ε 個冗余驅動使得rank(GT)= 6，奇異位形即可消除。根據(jù)文獻［12］不難得到冗余驅動時機構的力雅可比矩陣

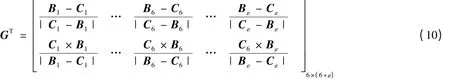
當機構為非冗余驅動時，有ε = 0，式(10)便為式(6)所示6 ×6 矩陣。

3.2 奇異位形的消除

黃真等［14］根據(jù)Grassmann 線幾何將并聯(lián)機器人機構的奇異位形分為一般線性叢奇異、第一類特殊線性叢奇異以及第二類特殊線性叢奇異。并指出Stewart 并聯(lián)機構的奇異位形絕大多數(shù)情況屬于一般線形叢奇異，即Merlet 5a［15］，力雅可比矩陣GT的秩為5;而對于第一類特殊線形叢奇異，即Merlet 5b［15］，力雅可比矩陣GT的秩也為5;而對于Stewart并聯(lián)機構的第二類特殊線形叢奇異，只有當動、定平臺重合時才會發(fā)生，此時雅可比矩陣的秩為3。

鑒于在實際應用過程中，動、定平臺一般不會出現(xiàn)重合情況，因此，文中只探討文獻［14］所述的前兩類奇異位形的消除方法，兩種情況對應的機構雅可比矩陣的秩均為5。根據(jù)前面的論述，為消除這兩類奇異位形，一般只需要添加一個冗余驅動支鏈，即式(10)中的ε = 1 即可。

4 數(shù)值實例

為進一步說明Stewart 并聯(lián)機構奇異位形的消除方法，下面舉例說明。

設機構的結構參數(shù)為:Rb= 20，Rm= 15 (為體現(xiàn)研究的一般性，結構尺寸取無量綱單位)、βb=βm=90°。現(xiàn)增加一個冗余驅動支鏈C7B7，該支鏈與動、定平臺相連的鉸鏈點分別是B7，C7。B7在動坐標系P-xyz 中的坐標(X'7，Y'7，0)，C7在固定坐標系O-XYZ 中的坐標(X7，Y7，0)，機構動平臺的姿態(tài)以ZYZ-歐拉角(φ，θ，ψ)描述。

當X7= X'7= Y7= Y'7= 0，即添加的驅動支鏈與動、定平臺鉸點位于平臺的幾何中心點。當P 點Z坐標值一定時，非冗余驅動時的機構雅可比矩陣的條件數(shù)在給定姿態(tài)時隨坐標(X，Y )變化如圖2 所示。冗余驅動時的機構力雅可比矩陣的條件數(shù)在給定姿態(tài)時隨坐標(X，Y )變化如圖3 所示。

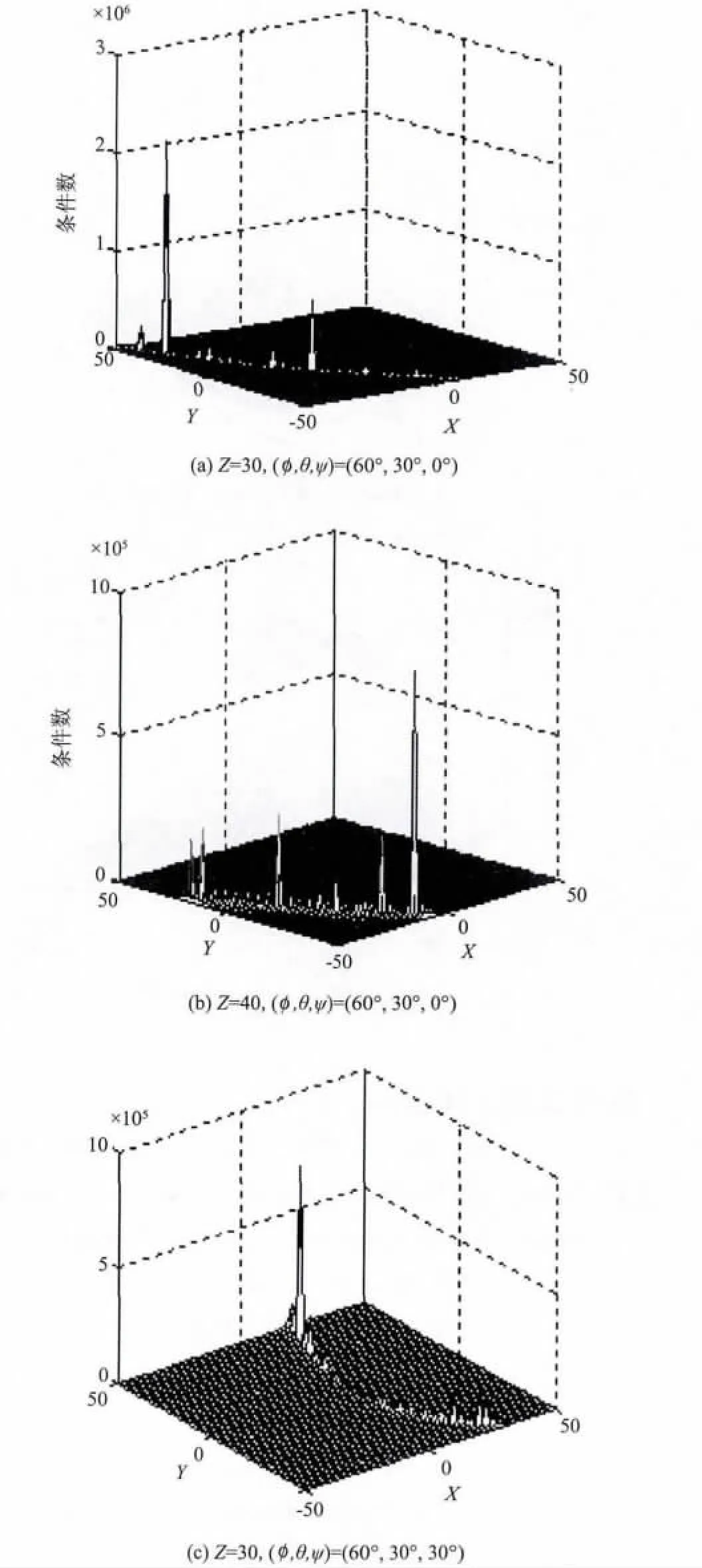
圖2 非冗余驅動時條件數(shù)隨(X，Y)的變化情況Fig.2 Condition number varies versus (X，Y)using non-redundant actuation

由圖2 和圖3 可以看出，非冗余驅動時機構在奇異位形與其附近處力雅可比矩陣條件數(shù)發(fā)生突變，并且機構處于奇異位形時的力雅可比矩陣條件數(shù)趨向于無窮大。增加冗余驅動后，無此現(xiàn)象的發(fā)生，機構運動學和靜力學性能得到很大提高，有效地消除了機構原有奇異位形的不良影響。

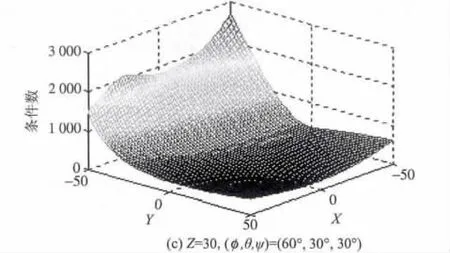
圖3 冗余驅動時條件數(shù)隨(X，Y)變化情況Fig.3 Condition number varies versus (X，Y)using redundant actuation

5 結 語

1)雅可比矩陣奇異值大小可以作為衡量并聯(lián)機器人機構運動傳遞性能的一項重要指標，奇異值越大，機構運動傳遞性能越好，當奇異值大小為無窮大時，機構處于奇異位形狀態(tài)。

2)對于Stewart 并聯(lián)機器人，通過在適當?shù)奈恢锰砑优c其他支鏈相同結構的冗余驅動，可有效減小機構雅可比矩陣的奇異值，極大地改善了機構的運動傳遞性能。該方法對其他類型并聯(lián)機構的奇異位形消除亦具有一定的參考價值。

3)由于Stewart 并聯(lián)機器人的奇異位形絕大多數(shù)情況下為Merler 5a 類型，只需通過添加一支如2)所述的冗余驅動，即可有效消除機構的奇異位形。

4)增加冗余驅動可有效地消除并聯(lián)機器人機構的奇異位形，但無疑會增加機器人控制的復雜性，因此下一步的目標將集中于冗余驅動控制并聯(lián)機器人控制算法方面的研究。

［1］黃真，趙永生，趙鐵石.高等空間機構學［M］.北京:高等教育出版社，2006.

［2］Nakamura Y，Hanafusa H. Inverse kinematic solution with singularity robustness for robot manipulator control［J］. Journal of Dynamic System.Measurement and Control，1986，108(9):163-171.

［3］Chiaverini S，Siciliano B，Egeland O. Review of the experiments on an industrial robot manipulator［J］. IEEE Transactions on Control Systems Technology，1994，2(2):123-134.

［4］郭盛，方躍法.避免設計位形下發(fā)生平臺奇異的三自由度轉動并聯(lián)機器人設計方法［J］. 中國機械工程，2005，16(1):8-11.

GUO Sheng，F(xiàn)ANG Yuefa. A structural synthesis approach for 3-DOF rotational parallel manipulators avoiding platform singularities in the design configuration［J］.China Mechanical Engineering，2005，16(1):8-11.(in Chinese)

［5］張彥斌，劉宏昭，胡鑫. 基于互易螺旋理論的無奇異完全各向同性移動并聯(lián)機構型綜合［J］. 機械工程學報，2008，44(10):83-88.

ZHANG Yanbin，LIU Hongzhao，HU Xin.Type synthesis of non-singular fully-isotropic translational parallel mechanisms based on theory of reciprocal screw［J］.Journal of Mechanical Engineering，2008，44(10):83-88.(in Chinese)

［6］張耀軍，張玉茹.基于Grassmann 線幾何的平面柔索驅動并聯(lián)機構奇異分析［J］.機械工程學報，2011，47(19):1-7.

ZHANG Yaojun，ZHANG Yuru. Singularity analysis of planar cable-driven parallel mechanisms with Grassmann geometry［J］.Journal of Mechanical Engineering，2011，47(19):1-7.(in Chinese)

［7］王玉新，李雨桐，潘雙夏. 一種規(guī)避并聯(lián)機構轉向點奇異問題的新方法［J］. 中國科學E 輯:技術科學，2008，38(1):125-136.

WANG Yuxin，LI Yutong，PAN Shangxia.A novel method of turning point singularity avoidance of the parallel mechanisms［J］.Science China:Technological Sciences，2008，38(1):125-136.(in Chinese)

［8］CHENG S，WU H，WANG C，et al.A novel method for singularity analysis of the 6-SPS parallel mechanisms［J］.Science China:Technological Sciences，2011，54(5):1220-1227.

［9］LI B，CAO Y，ZHANG Q，et al. Position-singularity analysis of a special class of the Stewart parallel mechanisms with two dissimilar semi-symmetrical hexagons［J］.Robotica，2013，31(1):123-136.

［10］LIU G F，WU Y L，WU X Z. Analysis and control of redundant parallel manipulators［C］// IEEE International Conference on Robotics and Automation.Seoul，Korea:IEEE，2001:3748-3754.

［11］楊建新，余躍慶.平面三自由度冗余并聯(lián)機構的驅動奇異性分析［J］.中國機械工程，2006，17(6):629-632.

YANG Jianxin，YU Yueqing.Actuator singularity analysis of planar 3-DOF redundant parallel mechanisms［J］.China Mechanical Engineering，2006，17(6):629-632.(in Chinese)

［12］張彥斐，宮金良，高峰.冗余驅動消除并聯(lián)機構位形奇異原理［J］.中國機械工程，2006，17(5):445-448.

ZHANG Yanfei，GONG Jinliang，GAO Feng.Theory of singularity elimination by redundant actuation for parallel mechanism［J］.China Mechanical Engineering，2006，17(5):445-448.(in Chinese)

［13］Saglia J A，DAI J S，Caldwell D G.Geometry and kinematic analysis of a redundantly actuated parallel mechanism that eliminates singularity and improves dexterity［J］.Journal of Mechanical Design，2008，130(12):124501.

［14］HUANG Z，ZHAO Y S，WANG J，et al. Kinematic principle and geometrical condition of general-linear-complex special configuration of parallel manipulators［J］.Mechanism and Machine Theory，1999，34(8):1171-1186.

［15］Merlet J P. Singular configurations of parallel manipulators and Grassmann geometry［J］. The International Journal of Robotics Reseach，1989，8(5):45-56.