LCL 濾波并網逆變器的新型電流控制策略

何春花， 惠 晶

(江南大學 輕工過程先進控制教育部重點實驗室，江蘇 無錫214122)

光伏并網逆變技術作為分布式發電系統并網的關鍵技術之一，對并網系統的安全穩定運行、電能質量控制以及電力系統的規劃都至關重要［1-2］。光伏逆變器的脈寬調制(PWM)過程中會產生大量的開關頻率次諧波，為提高并網電流質量，需要采用適當的濾波器［3］。常用濾波器有L 型、LC 型、LCL型濾波器。LCL 濾波器所需總電感量比L 和LC 濾波器小得多，運用LCL 濾波器不僅能降低成本，減小濾波器的體積和質量，還能提高動態響應能力，對諧波的抑制效果佳，具有較好的應用前景［4-5］。但LCL 濾波器是一個3 階系統，本身存在著諧振問題而使系統不穩定。為了抑制諧振必須增加阻尼環節，而阻尼環節會帶來系統功率損耗［6］。為提高逆變效率和供電質量，可以采用合適的控制方案來實現有源阻尼降低系統功率損耗同時抑制諧振，因此優化逆變器的控制策略是近年來研究的一個重點和熱點。

文中采用并網電流和電容電流雙閉環控制策略，用電容電流內環來增加系統阻尼，以有效抑制諧振發生，用進網電流外環控制實現對并網電流的直接控制，可保證高的進網電流功率因數。通過仿真驗證，該方法具有良好的穩態和動態性能。

1 LCL 拓撲及并網電流控制策略

1.1 系統結構模型

LCL 濾波器以其所需電感量小、對高頻諧波抑制能力強等優點受到廣泛認可［7-8］。圖1 所示是采用LCL 濾波器的三相并網逆變器拓撲結構，由逆變器側電感L1、濾波電容C 和網側電感L2組成，其中Udc是直流母線電壓。控制方案采用并網電流作為外環，實現對并網電流的直接控制，可有效提高進網電流功率因數。電容電流作為內環，增加系統阻尼，抑制系統振蕩，提高系統的動態性能，同時結合同步矢量電流比例-積分(Proportional Integral，PI)調節器的SVPWM 方法，實現開關管的導通與關斷，使電壓源型LCL 濾波并網逆變器輸出電流的相位完全與電網電壓相位一致，保證向電網輸送電流的總諧波含量符合標準要求。

圖1 三相LCL 濾波并網逆變器Fig.1 Three-phase grid-connected inverter with LCL filter

1.2 PWM 并網逆變器的數學模型

PWM 可以同時實現變頻變壓反抑制諧波，因此在交流傳動及其它能量變換系統中得到廣泛應用，并一直是研究的熱點。而逆變橋開關管的控制模式又多種多樣，因此不考慮具體開關器件的類別，建立PWM 逆變器的通用數學模型對系統仿真設計和驗證具有重要意義。

為便于分析，作如下假設:(1)電路開關器件為理想開關元件;(2)所有續流二極管導通壓降均為零;(3)在換相過程中，忽略晶體管開關時吸收電容的影響;(4)三相電網電壓對稱且穩定，直流側電壓紋波為零。這里首先用開關函數建立三相逆變全橋環節的通用數學模型，然后建立濾波器的數學模型，把兩者直接相連即可構造出仿真模型。

定義各個開關函數:Sj= 1，第j 個開關導通，Sj= －1，第j 個開關斷開，j = 1，2，3，4，5，6。則

其中k = 0，1，…，7。

設O 為直流電源負極電位點，求得每相逆變橋輸出點a，b，c 到直流電源負極之間的電壓與開關函數之間的關系為

根據基爾霍夫電壓定理，由圖1 可知

由先前假設可知，三相電壓和負載是對稱的，即UaN+ UbN+ UcN= 0 所以有

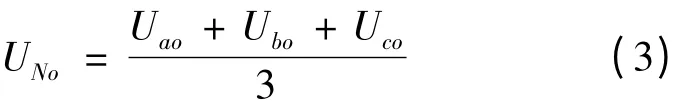
由式(1)～(3)定理可得

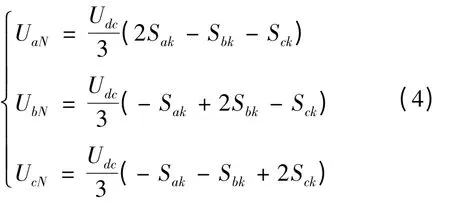
1.3 LCL 濾波器的數學模型

LCL 濾波器作用是利用加入的電容支路為高頻開關紋波電流提供低阻通路，起到對高頻分量的旁路作用，減少注入電網的紋波電流。分別選擇電感L1中的電流i1k、電感L2中的電流i2k和濾波電容電壓Uck為狀態變量，其中k = a，b，c。圖2 為每相LCL濾波器的傳遞函數結構圖。

圖2 每相濾波器模型Fig.2 Each phase filter model

其狀態空間方程為

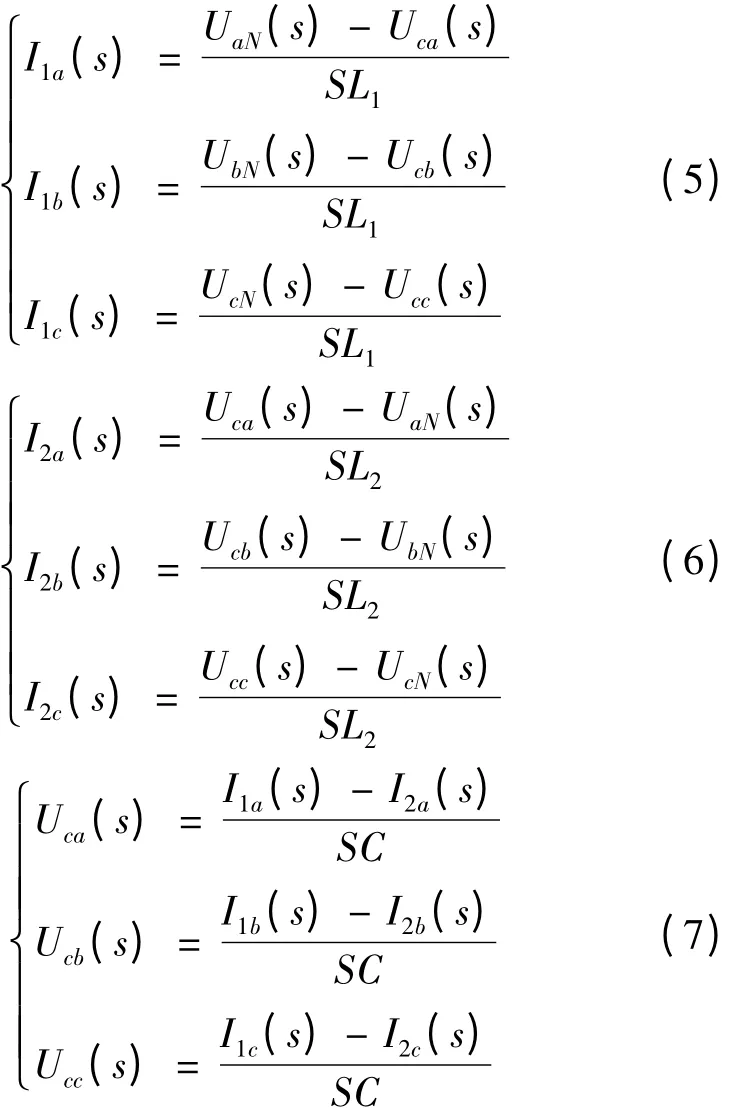
2 控制策略及其穩定性分析

2.1 系統原理框圖及其穩定條件分析

從上述狀態方程式可知，各相傳遞函數之間是相互獨立的，并且其形式和單相逆變器狀態方程是一致的。因此，該逆變電源系統的控制策略及其穩定性分析討論可基于單相逆變器展開，為實現交流變量控制的零穩態誤差，控制器采用無差拍控制器，能夠實現無差跟蹤，具有良好的動態性能［9］。

對于三相并網逆變器而言，控制策略的實現是通過變量導數預測控制結果，這樣使用動態響應較快和魯棒性較強的PI 調節器即可實現并網電流的無靜差調節，使并網逆變器向電網輸出高質量并網電流，且基于SVPWM 的同步矢量電流PI 控制方案對一些非線性因素的影響也具有一定的補償功能［10］。

圖3 給出文中所提逆變器并網運行控制方法的結構，圖4 所示為電流雙閉環控制的等效結構。

為便于系統的穩定性分析，設電流反饋均為單位反饋。其中，逆變橋相對于直流電源的等效輸出增益為KPWM;比例控制環節為K。

圖3 電容電流環的主要作用是增加系統阻尼，以有效抑制諧振發生，其控制器只需用比例控制即可，K 為比例系數。利用自動控制理論中的等效變換法將圖3 等效變換，簡化得到并網電流控制的等效結構如圖4 所示。

由圖4 可以看出，并網電流的質量不僅受電網電壓自身諧波含量的影響，而且與電流控制策略有關。

圖3 電流雙閉環控制結構Fig.3 Current double closed-loop control structure diagram

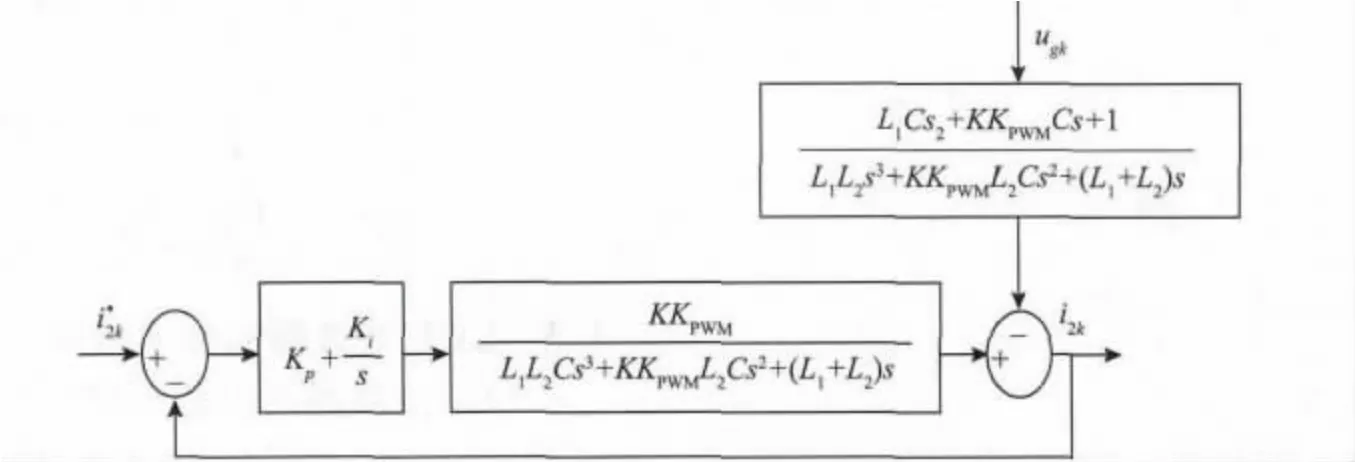
圖4 電流雙閉環控制的等效結構Fig.4 Structure diagram of the double closed-loop of current

文中主要研究電流控制策略對并網電流的影響，系統的開環傳遞函數為

為求出系統的穩定條件，由式(8)得到閉環傳遞函數

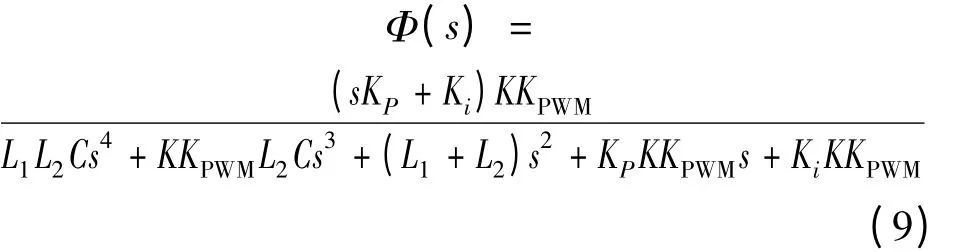
閉環系統傳遞函數的特征方程為

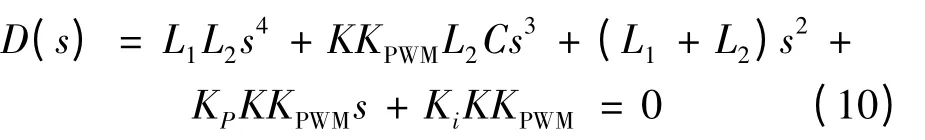
根據Hurwitz 穩定判據，系統穩定的充要條件為式(10)各項系數全大于零，且

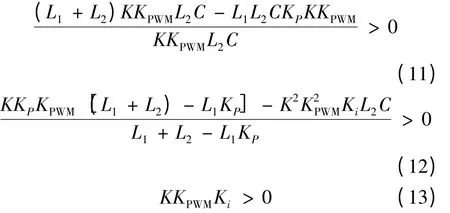
由式(11)～(13)可以解出KP，Ki的臨界值。

2.2 系統閉環參數設計與性能分析

LCL 濾波器為3 階電路，系統穩態性能和動態性能受閉環參數的影響較大，所以設計的控制器參數要保證系統有足夠的穩定裕度。根據控制原理，實際工程中一般要求幅值穩定裕度h 為5 ～10 dB，相角穩定裕度為25 ～60。由于文中控制策略中內環主要作用是增加系統阻尼，因此可以忽略高階項，其特征阻尼比近似表示為

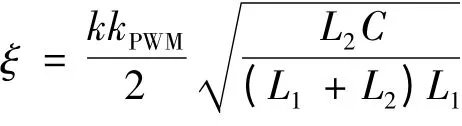
k 越大，系統阻尼比越大，諧振抑制效果越好，但是阻尼過大，系統快速性差，調節時間長。工程上往往取0.5 ＜ξ ＜1，但為了兼顧系統的阻尼效果和動態性能，一般取0.6 ＜ξ ＜0.8。考慮到實際系統參數L1，L2，C 與設計值可能存在一定程度的偏離，因為LCL 濾波器是利用了電感與電容對不同頻率分量所呈現阻抗差異性的特點。與L 型濾波器相比，增加了濾波電容C 和網測電感L2，引入C 和L2后可對高次諧波的逆變器橋輸出電流進行并聯阻抗分流，濾波電容C 為高頻部分提供低阻通路，從而有效降低入網電流中的諧波電流分量。但是，C 參數越大其需要的無功功率越多，相應導致逆變器的功率因數降低。通常用折衷值ξ = 0.707［11］。不同的L1，L2與C對濾波器頻率特性的影響如圖5 和圖6 所示。

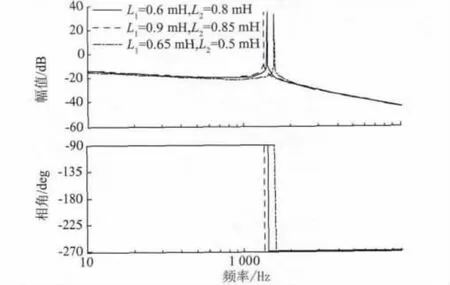
圖5 C 不變L1，L2 取不同值的濾波器頻率特性Fig.5 Filter frequency characteristic for constant C and different，L1 and L2

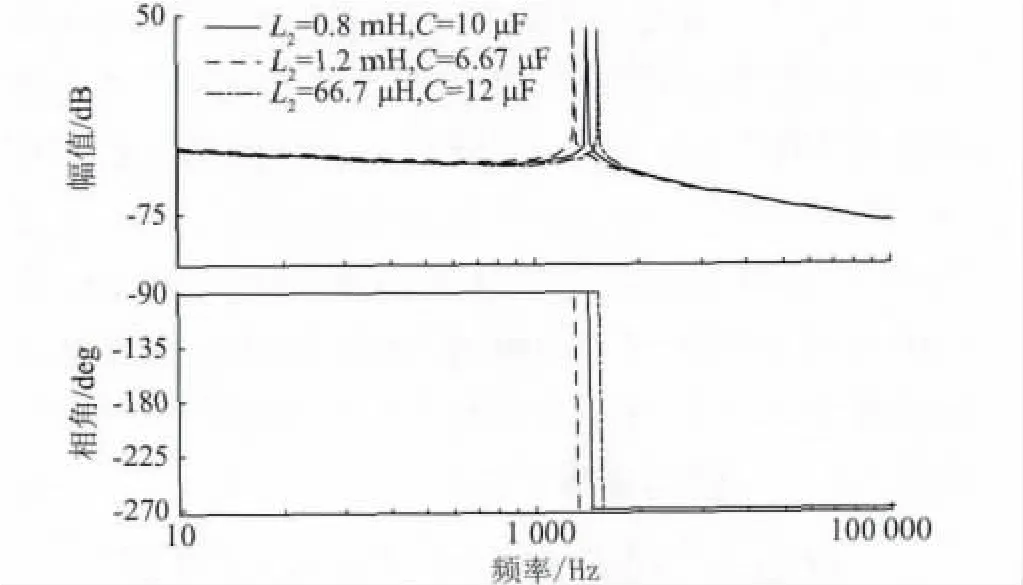
圖6 L1 不變L2，C 取不同值時濾波器頻率特性Fig.6 Filter frequency characteristic when constant L1 and different，C and L2

圖5 是C = 10 μF 時的頻率特性。可以看出，組合2 的濾波特性最好，組合3 的濾波特性比組合1 的差，雖然前者的L1比后者大，逆變橋電流中的高頻含量相對較小，但過小的L2影響了分流效果，導致最終的濾波效果較差。

圖6 是L1= 0.6 mH 不變且保證XC/XL2不變，改變L2與C 大小時濾波器的頻率特性。從圖中可以看出，3 種組合的頻率諧振點不同，在轉折頻率以上的高頻階段，3 種組合的濾波性能幾乎相同。改變L2后，由于改變了總的濾波電感量，3 種組合的低頻段增益存在差異，濾波電感量越小則低頻增益越高，電感造成的電壓損越低。外環PI 調節器的設計方法比較多，文中結合KP，Ki的邊界范圍采用“振蕩指標法”獲得一組參數，以確保系統具有足夠的穩定裕度，同時盡可能兼顧系統的動態性能。

3 仿真驗證

為驗證電感電流和電容電流雙閉環控制策略的優越性，運用Matlab/Simulink 軟件對LCL 并網逆變器的雙閉環電流控制進行模型搭建并對其進行仿真，系統主要仿真參數如表1 所示。

表1 仿真參數Tab.1 Simulation parameters

圖7 表示穩態運行時電網電壓、并網電流和網側電感電流的仿真波形。圖8 是A 相并網電流的頻譜分析。可以看出，網側電流的相位與電網電壓非常接近，系統實現了高功率因數并網運行，并且網側電流THD 為1.02%，與網側電感電流獨立控制相比，很好地抑制了入網電流的諧波含量，獲得了預期的電流輸出效果。為驗證系統的動態性能，在0.03 s 時突然增加并網電流。系統的動態仿真波形如圖9 所示。可以看出，系統在半個周期內即可達到穩定狀態，說明動態響應較快。

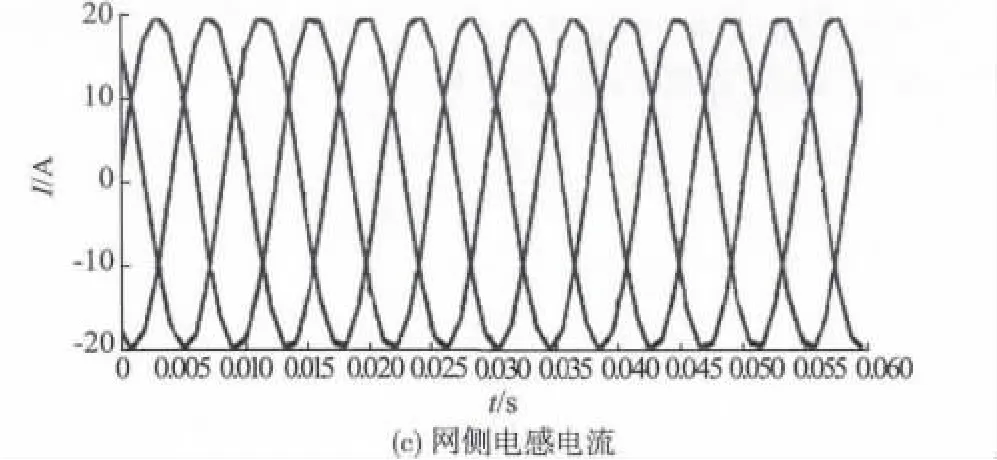
圖7 穩態時仿真波形Fig.7 Simulation waveform in steady-states

圖8 a 相并網電流FFT 分析Fig.8 FFT analysis of the A-phase grid-connected current

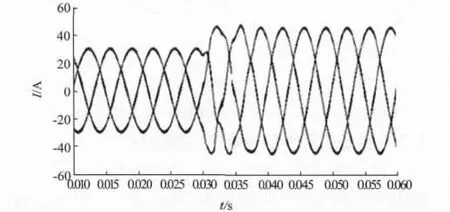
圖9 輸出電流的動態仿真波形Fig.9 Dynamic simulation waveform of the output current

4 結 語

采用并網電流直接閉環控制的LCL 濾波逆變器并網系統存在諧振尖峰，易造成系統不穩定。文中采用網側電感電流和電容電流相結合，提出并網電流作為外環、電容電流作為內環的控制策略。通過仿真表明，該控制策略既可有效抑制入網電流諧振和實現進網電流的高功率因數運行，同時又具有良好的穩態和動態性能，且方案簡便易行。

［1］特奧多雷斯庫.光伏與風力發電系統并網變換器［M］.周克亮，王政，徐青山，譯.北京:機械工業出版社，2012.

［2］張興，曹仁賢.太陽能光伏并網發電及其逆變控制［M］.北京:機械工業出版社，2011.

［3］陳東.并網逆變器系統中的重復控制技術及其應用研究［D］.杭州:浙江大學，2012.

［4］王國君.基于虛擬磁鏈直接功率控制的并網逆變器的研究［D］. 哈爾濱:哈爾濱工業大學，2008.

［5］趙方平，楊勇，阮毅，等.三相并網逆變器直接功率控制和直接功率預測控制的對比［J］. 電工技術學報，2012，27(7):212-220.

ZHAO Fangping，YANG Yong，RUAN Yi，et al. Comparative study for direct power control and direct power predictive control in three-phase grid-connected inverters［J］.Transactions of China Electrotechnical Society，2012，27(7):212-220.(in Chinese)

［6］韓詠茹，薛士龍，鄧勇智.基于LCL 濾波的逆變器并網電流控制策略研究［J］.電源學報，2014，1(51):103-110.

HAN Yongru，XUE Shilong，DENG Yongzhi.Current control strategy for the grid-connected inverter with LCL filter［J］.Journal of Power Supply，2014，1(51):103-110.(in Chinese)

［7］郭小強，鄔偉揚，顧和榮，等.并網逆變器LCL 接口直接輸出電流控制建模及穩定性分析［J］. 電工技術學報，2010，25(3):102-109.

GUO Xiaoqiang，WU Weiyang，GU Herong，et al. Modelling and stability analysis of direct output current control for LCL interfaced grid-connected inverters［J］.Transactions of China Electrotechnical Society，2010，25(3):102-109.(in Chinese)

［8］TANG Yi，Poh Chiang Loh，WANG Peng，et al. Exploring inhere damping charae tefisfic of LCL-filters for three-phase gridconneetod voltage source inverters［J］.IEEE Tmnsactions on Power Electronics，2012，27(3):1433-1443.

［9］ZHANG X，Spencer J W，Guermro J M.Small signal modeling of digitally controlled grid-connected invertem with LCL filter［J］.IEEE Transactions on Industrial Electronics，2013，60(9):3752-3765.

［10］艾淑云，翟登輝，李獻偉，等.基于無差拍算法的單相光伏并網逆變器的研究［J］.通訊電源技術，2014，31(3):4-6.

AI Shuyun，ZHAI Denghui，LI Xianwei.Research on single-phase photovoltaic grid-connected inverter based on deadbeat control［J］.Telecom Power Technology，2014，31(3):4-6.(in Chinese)

［11］Jeong Hea-Gwang，Lee Kyo-Beum，Choi S. Performance improvement of LCL filter based grid-connected inverters using PQR power transformation［J］.IEEE Trans On Power Electronics，2010，25(5):1320-1330.