基于KCPSO 算法對閩西地區崩塌地判釋

李隘優

(閩西職業技術學院 計算機系，福建 龍巖364021)

在判釋崩塌地中，傳統通常采用實地調查方法，能夠準確判釋崩塌地，但較多依賴專家經驗，具有主觀性;同時確定模型需要收集大量準確的工程地質和水文地質數據，需要足夠的歷史數據才能做出準確的評價預測，而且只適合較小區域評價，對于人力無法到達或面積過大的災后地區要進行分析評估仍有很大困難［1-2］。為了提高分類精度，目前許多學者采用組合的算法，如采用粒子群優化(Particle Swarm Optimition，PSO) 方 法［3-4］與K-means 聚類(KPSO)算法［5-7］相結合，充分利用不同算法的優點，對于線性可分數據能夠比較精確地找到聚類的個數，但它在線性不可分情況下找到的聚類個數和初始聚類中心往往是不理想的。文中提出將K-means 聚類分析、混沌搜索與粒子群最優化技術相結合形成混合群聚算法(KCPSO)，以KCPSO 作為分類器判釋遙測影像數據，以非監督方式對閩西大范圍區域進行崩塌與不崩塌二元快速判釋。并將KCPSO 與KPSO，CPSO 算法加以比較，進而分析出不同有效分類器的差異。

1 K-means 聚類算法

粒子群最優化算法(PSO)是一種以族群動力學為基礎的演化式計算法則，它的基本概念來自鳥群或魚群的社會行為的模擬。在一個社會化的群體中，每一個個體的行為不但會受到其過去經驗和認知的影響，同時也會受到整體社會行為影響。在粒子群最優化算法中每一個個體在搜尋空間中各自擁有其方向和速度，并且根據自我過去經驗與群體行為進行機率式的搜尋策略調整。其作法如下:

式中:d 為搜尋空間中變量的維度;i 為群體中的個體;vi為速度向量;X 為位置向量。Pi為個體所經歷過最優解位置;Pg為個體所處整個鄰域所記錄的最佳解位置;c1，c2分別為自我認知學習因子與社會模式學習因子。

利用PSO 的搜尋能力協助人們在n 維的歐幾里德空間Rn中，依數據的相似特性自動地將N 個樣本數據區分成k 類群聚，并分別決定其群聚中心向量。首先，令PSO 演化族群中的每一個個體編碼值為實數值所構成的字符串序列，它代表了k 個群聚中心。對于n 維空間而言，每一個個體的長度是k·n 個字符。而隨機產生的初始族群也就代表了各組不同的群聚中心向量值。

確定個體的字符串編碼后，再根據下列KPSO算法步驟執行:

1)決定初始族群個體數目以及相關參數。對第i 個體而言，它具有隨機給定的位置以及速度。此處，個體的位置值即是所欲求得的各群聚的群聚中心值。

2)計算每一個個體的適應函數值。分別度量數據集中數據樣本與群聚的距離，并依下面條件將樣本歸類至其最接近的群聚，文中采用所提出的距離度量相似性以得到目標函數，而系統適應函數則定義如下:

其中

且

3)將每一個個體求得的解與其經驗中記錄的個體最佳解進行比較，若目前求得解比之前最佳結果更佳，則以目前解取代個體最佳解。此外，若目前求得的解優于群體最佳解，則將群體最佳解重設為目前的結果。

4)將群體最佳解求值以單步的K-means 算法取代

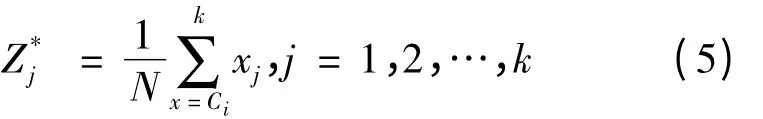
為了節省計算量，同時維持PSO 能繼續往搜尋空間的近似最佳解，文中建議在整體迭代過程的前幾次迭代中執行本步驟即可。

5)根據式(2)、式(3)修改族群中各個體的位置和速度。

6)重復2)～5)等步驟，直至滿足所設定的終止條件后結束循環的執行。

2 混沌粒子群優化算法

混沌粒子群優化算法(CPSO)的基本思想是將混沌狀態引入到優化變量中，并把混沌運動的遍歷范圍載波變換到優化變量的取值范圍，再把得到的混沌變量表示成粒子，根據粒子之間的合作與競爭進行搜索，到一定階段給群體最優位置附加一個微小的混沌擾動，通過不斷地更新粒子的速度和位置，最后求得問題的最優解［8］。

文中選用Logistic 映像［9］生成混沌變量，即

采用下式所示的線性映射將混沌變量變為優化變量

其中，b，a 分別為優化變量y 的取值區間上限與下限。優化搜索過程中，隨著迭代的進行，混沌變量在［0，1］區間遍歷，對應的優化變量則在相應的問題研究區間遍歷，搜索問題的最優解。

根據混沌搜索的思想，如果當前迭代次數大于最大迭代次數的2/3 時，應在當前最優解中加入一個微小的混沌擾動量。

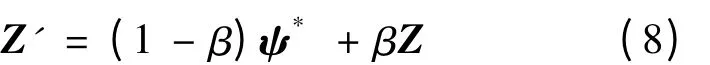
其中，β 為一個調節參數，0 ≤β ≤1;Z'為對應當前最優解向量映射X*加了微小擾動后的混沌向量;Z為由Logistic 映射產生的混沌序列向量;ψ*為當前最優解向量X*映射到［0，1］區間后形成的最優混沌向量，即

在CPSO 方法中，PSO 的gbest(t)可以被具有更好的適應度值的chaos(gbest(t))取代。

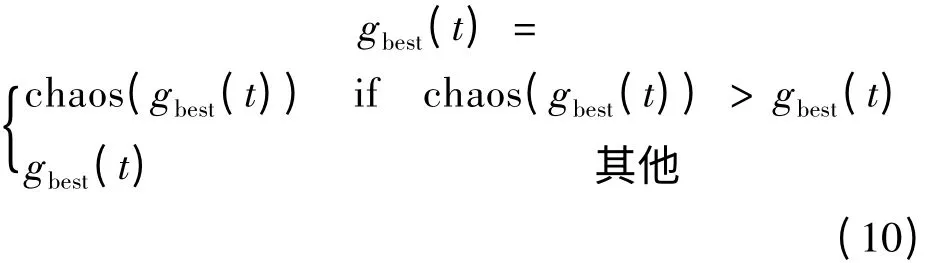
式中:t 為迭代次數;gbest(t)為群體中適應度最優的粒子位置;chaos(gbest(t))為經過混沌搜索過程粒子的適應度值;“＞”是指chaos(gbest(t))適應度值比gbest(t)更好。

3 混合群聚算法

在PSO 結合K-means 將幫助PSO 聚類過程收斂，在PSO 采用混沌搜索將有助于提高gbest，文中提出基于K-means 與混沌搜索PSO 算法(KCPSO)，將利用它們互補性特點去搜尋群體的最佳解決方案。因此，KCPSO 算法的建立應包括公式(1)、式(2)、式(3)、式(5)和式(10)。

在進化的初始階段，對粒子進行了多樣化混沌序列初始化，從而實現更好的gbest值，然后PSO 對pbest與gbest更新。在群體每次迭代過程中，混沌搜索和K-means 都按順序執行，因此，PSO 的并行特性、遍歷性、不規則性同混沌的偽隨機性和K-means 聚類屬性結合在一起，形成KCPSO 特性。圖1 為模擬CPSO 遷移gbest過程。

圖1 模擬CPSO 遷移gbest 過程Fig.1 Simulation process of CPSO migration

在一般情況下，KCPSO 會產生一定的規則指導群遷移，群成員將沿著這種關聯規則進行進化。例如，混沌搜索可能會發現一個更好的粒子，以取代PSO 的gbest，與此同時包括適應度最小粒子的質心將不可避免地被消除。最終，更好gbest與聚類中心將有效地提高。

4 實驗與分析

文中收集了2009 年閩西地區影像，全幅為12 000 m ×12 028 m，ASCII 矩陣為6 000 ×6 014 個像素，衛星影像經裁切劃分出一個樣本學習區，一個樣本驗證區。學習區長為3 098 m，寬為3 036 m，ASCII 矩陣為1 549 ×1 518 個像素，其地型包含了林地、草地、水體、崩塌地、裸露地;驗證區長為2 855 m，寬為3 035 m，為了達到快速判釋的目的，文中將驗證區矩陣縮小，以達到快速判釋的目的，像元轉換后驗證區的像元從2 m ×2 m 放大為5 m ×5 m，轉成ASCII 驗證區矩陣為571 ×607 個像素。為了確保研究的可行性，前往現場探勘4 次，拍攝一系列的現場相片，與衛星影像經仔細比對后，確認120 處數據確實為崩塌和非崩塌地正確樣本數據。

首先建立研究區內崩塌地的空間數據庫，先取樣60 個樣本點，將樣本分為崩塌與非崩塌，其中包含林地、草地、水體、巖石地。將各時期衛星圖的4 個原始波段和8 個影像中植生或土壤的輔助信息取出，由波段數據中萃取出重要因子。初期將各時段的影像分為兩類:崩塌地與非崩塌地。從上述數據來源得到崩塌地的知識規則，并套用于驗證區中，描繪出該地區哪里有崩塌的情形或是哪里有可能崩塌并設立崩塌危險區。本實驗參數c1，c2取2.05，最大迭代次數為100，種群適應度方差閾值0.5，混沌系數μ 取0.8，其他為默認值。在二元判釋中，將60 筆學習樣本分別代入不同的分類器中進行分類，最后得到兩類(崩塌地與非崩塌地)的資料群聚中心，以這些群聚中心作為測試的決策依據。知識規則建立之后，將驗證區共三十多萬個像元分成兩類，圖2 為其判釋結果，深色部分為崩塌地，其他為非崩塌。

由于分類成眾多類別，在分類時常發生類別與類別間的混淆。由于坡地滑動與土壤自身穩定性有關，坡度是控制邊坡穩定性的重要因子，也是山坡地穩定最直接相關的地形條件，坡度越陡，越容易發生崩塌，發現坡度大于56%(約24.9°)的崩塌地具有較高的不穩定性，極易發生崩塌，因此崩塌地坡度閾值取24.9°，將地貌重新進行分類，剔除河道和裸露地的巖石，此巖石多半被誤判為崩塌地，由于閾值的建立，改正易混淆的類別，以提升影像整體判釋精度。

圖2 不同算法判釋結果比較Fig.2 Comparison of the interpretable results in different algorithms

為了比較不同算法的性能，表1，表2 對4 種聚類算法PSO，KPSO，CPSO ，KCPSO 在同一區域進行分類比較。

表1 判釋的準確率Tab.1 Accuracy of interpretable in different algorithms

表2 經類別轉換前后判釋的準確率Tab.2 Accuracy of interpretable before and after conversion by category

由表2 可以看出，PSO 聚類的過程是很不穩定的，容易早熟，容易收斂到局部最優解，而且聚類的過程中可能會有振蕩的情況出現，在較小適應度值出現時可能會有較差的情況出現，因此判釋率不高;而對粒子群進行相應的改進后，先利用K-means進行聚類或混沌搜索，然后再利用粒子群，這樣就在一定程度上改善了局部收斂，而且收斂的也較快，得到了較優的適應度值，整體判釋率有所提高。KCPSO 算法則明顯的優于粒子群，整體判釋率提高了10% 以上，這說明用基于KCPSO 進行聚類，其目標函數收斂性能更好。不同分類器若采用崩塌地坡度閾值重新過濾，準確率都提高20% 左右，KCPSO達到的94.09%。

5 結 語

文中利用KCPSO 針對崩塌地進行分群判釋，以基于K-Means 與混沌分類進行處理可算出影響崩塌地的重要屬性，于災后能快速掌握其資料以預測下次崩塌的發生進而加以防范，與利用不安定指數法配合崩塌潛勢因子規劃出崩塌潛勢圖或統計多變量分析相比，本方法能選出重要屬性以減少數據量即可預測崩塌發生。本研究經崩塌實證分析后，還可在閩西地區范圍進行實測，檢驗是否為當時崩塌地范圍，因此日后可利用遙測技術實時快速分析的特性，配合數據萃取技術，繪出崩塌地預測判斷圖，對于防范崩塌地發生，可以作為其參考指標。

［1］曾山.模糊聚類算法研究［D］.武漢:華中科技大學，2012.

［2］孫樹林，余文平，劉小芳，等.基于信息熵與KPSO 聚類法滑坡敏感性分析［J］.環境保護科學，2014，40(6):88-97.

SUN Shulin，YU Wenping，LIU Xiaofang，et al. Landslide susceptibility analysis based on entropy and KPSO clustering［J］.Environmental Protection Science，2014，40(6):88-97.(in Chinese)

［3］周馳，高海兵，高亮，等.粒子群優化算法［J］.計算機應用研究，2003，12(l):7-11.

ZHOU Chi，GAO Haibing，GAO Liang，et al. Particle swarm optimization(PSO)algorithm［J］. Application Research of Computer，2003，12(1):7-11.(in Chinese)

［4］吳昌友，王福林，馬力.一種新的改進粒子群優化算法［J］.控制工程，2010，17(3):359-362.

WU Changyou，WANG Fulin，MA Li.Improved particle swarm optimization algorithm［J］.Control Engineering of China，2010，17(3):359-362.(in Chinese)

［5］王輝，張望，范明. 基于集群環境的K-Means 聚類算法的并行化［J］. 河南科技大學學報:自然科學版，2008，29(4):42-45.

WANG Hui，ZHANG Wang，FAN Ming. Research on parallelism of K-Means clustering algorithm based on cluster［J］. Henan University of Science and Technology:Natural Science，2008，29(4):42-45.(in Chinese)

［6］韓凌波，王強，蔣正峰，等.一種改進的K-Means 初始聚類中心選取算法［J］.計算機工程與應用，2010，46(17):150-152.

HAN Lingbo，WANG Qiang，JIANG Zhengfeng，et al. Improved K-Means initial clustering center selection algorithm［J］.Computer Engineering and Applications，2010，46(17):150-152.(in Chinese)

［7］王慧，申石磊.一種改進的特征加權K-means 聚類算法［J］.微電子學與計算機，2010，27(7):161-163.

WANG Hui，SHEN Shilei. An improved feature weighted K-Means clustering algorithm［J］. Microelectronics and Computer，2010，27(7):161-163.(in Chinese)

［8］沈洪遠，彭小奇，王俊年，等.基于混沌序列的多峰函數微粒群尋優算法［J］.計算機工程與應用，2006，42(7):36-38.

SHEN Hongyuan，PENG Xiaoqi，WANG Junnian，et al. A PSO algorithm based on chaos sequence for multi-modal function optimization［J］.Computer Engineering and Applications，2006，42(7):36-38.(in Chinese)

［9］梁慧.混沌粒子群優化算法的分析與應用［D］.廣州:廣東工業大學，2011.