某大跨度斜拱橋吊桿張拉控制分析

穆懷天， 朱召泉 ， 李 歡

(河海大學 土木與交通學院，江蘇 南京210098)

隨著我國社會經濟的發展，全國各地出現了各種采用吊桿作為傳力結構的異型拱橋，稱之為吊桿張拉拱式結構。這種受力方式使得拱肋的形式變得多樣化。其施工的主要順序為:先設置臨時支架施工拱肋，然后再施工橋面系，最后通過張拉吊桿將橋面結構與承重結構形成一體。拱式結構內力通過吊桿張拉來傳遞，當吊桿索力滿足設計要求時，結構的各項力學指標也相應地滿足設計要求。

結構剛度較小的鋼箱梁系桿拱橋在施工過程中，吊桿拉力的調整是十分重要的工作，各吊桿的最終拉力不僅直接關系到成橋的線形和成橋的受力狀態，而且也直接影響著橋梁外形的美觀和安全性能。但是各吊桿拉力的確定又是困難的工作，因為各根吊桿在每次張拉的同時會伴隨著拱肋、橋面系主梁的相對位移，從而引起前期吊桿張拉力的松弛，呈現非線性變化，使得此類系桿拱橋的吊桿索力在張拉作業結束后難以達到設計要求。此外，索力的調整工作也很復雜，會嚴重影響到施工進度。所以整個施工過程中，正確確定吊桿張拉過程中各吊桿所需施加的預應力就顯得非常關鍵［1］。

目前在橋梁工程吊桿張拉計算領域常用的方法有正裝法、倒裝法、無應力狀態法和多次張拉的影響矩陣法［1］。國內外有很多學者對這個問題進行了研究與改進。

肖汝誠等通過廣義影響矩陣概念，將斜拉橋優化的目標函數統一用索力變量與廣義影響矩陣表示，導出斜拉橋索力優化的影響矩陣法。這種方法可用于施工階段的索力優化和成橋后的索力調整;其又以靜載彎曲能量代價最少原理來確定斜拉橋的合理索力，通過倒裝法可以方便地確定斜拉索的施工張拉力［2］。

秦順全院士成功地將無應力狀態法應用于十多座大橋的施工控制。無應力狀態法引出無應力曲率和無應力索長這個不變量及其計算方法，并利用該不變量準確地建立了施工過程和最終成橋狀態之間的聯系，使得施工過程中的受力和變形之間的關系更加明確［3］。

李洪波等通過研究確定了系桿拱橋合理的吊桿張拉力傳統計算方法，提出基于影響矩陣法、綜合剛性吊桿法和自動調索法來確定系桿拱橋的成橋吊桿內力的方法［4］。

1 工程背景簡介

張家港市錦豐鎮為打造以城市公園化為核心目標的綜合性現代化生態新城，根據市政規劃，在華山路往西跨越一干河位置建設一座人行景觀橋梁［5］。一干河擬規劃河道寬度為120 m，新建橋梁主跨采用105 m 的下承式異形鋼拱橋，邊跨約為12.5 m，橋梁的跨徑布置為12.5 m + 105 m + 12.5 m，全橋共長131.94 m;橋梁范圍內道路平面均位于曲線范圍，曲線半徑分別為29.1 m 和108 m;主梁以跨中為對稱中心，采用雙向人字坡;相對于人行橋，拱肋向外傾斜，傾斜角度為75°，拱肋拱軸線在其自身傾斜面內為二次拋物線，矢高為26.25 m，跨徑為105 m，矢跨比為1/4，如圖1 所示。全橋共有19 根吊桿，呈對稱布置，由中間向兩側依次定義為DS1，DS2(2＇)DS3(3＇)，…，DS10(10＇)，如圖2 所示。

圖1 一干河人行景觀橋立面Fig.1 Yigan river landscape footbridge elevation

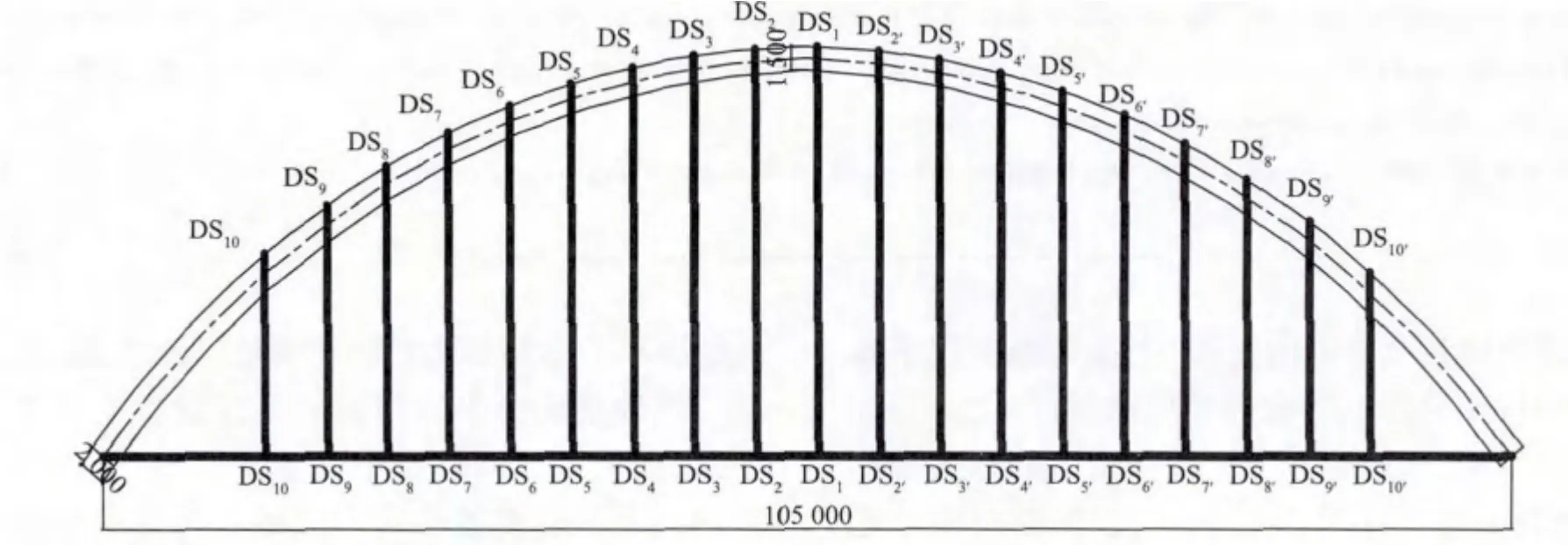
圖2 吊索編號示意Fig.2 Schematic diagram of the sling

在施工中，吊桿是分批張拉的，由DS1開始依次向兩側張拉。由于一根吊桿的張拉會使整體結構發生變形，內力會重新分布，從而造成前期張拉吊桿的束力與后期張拉吊桿的束力之間相互影響，使得原本張拉好的吊桿產生應力松弛，達不到滿足控制的束力條件。

而每一次新的調整又會產生新的內力重分布，這使得吊桿張力的調整變得非常繁瑣［6］。因此有必要考慮在吊桿相互影響的前提下，通過計算確定張拉的順序與張拉力的大小，使得完成一個階段的張拉后，各吊桿均可達到此階段的張拉設計值，不必進行調整［7］。

2 Ansys 建模與倒裝法控制張拉力計算

2.1 Ansys 建模

該大跨度斜拱橋的拱肋和橋面主梁均為鋼箱型截面，有限元建模時，為提高計算精度，并使各單元的受力特性與實際結構一致，主拱、主梁、加勁肋、橫隔板以及拱梁連接段均采用shell63 單元模擬;拱腳與基礎預埋段內部密實灌注的混凝土采用solid65 單元模擬;吊桿只能承受拉力作用，故采用link10 單元模擬，并設定KEYOPT(3)= 0;支架采用pipe16 單元模擬。拱、橋結構整體模型共劃分為193 421 個節點，199 688 個單元。

2.2 倒裝法控制張拉力計算

2.2.1 倒裝計算法運算步驟

1)建立滿足既定橋梁狀態的有限元模型，如圖3 所示。

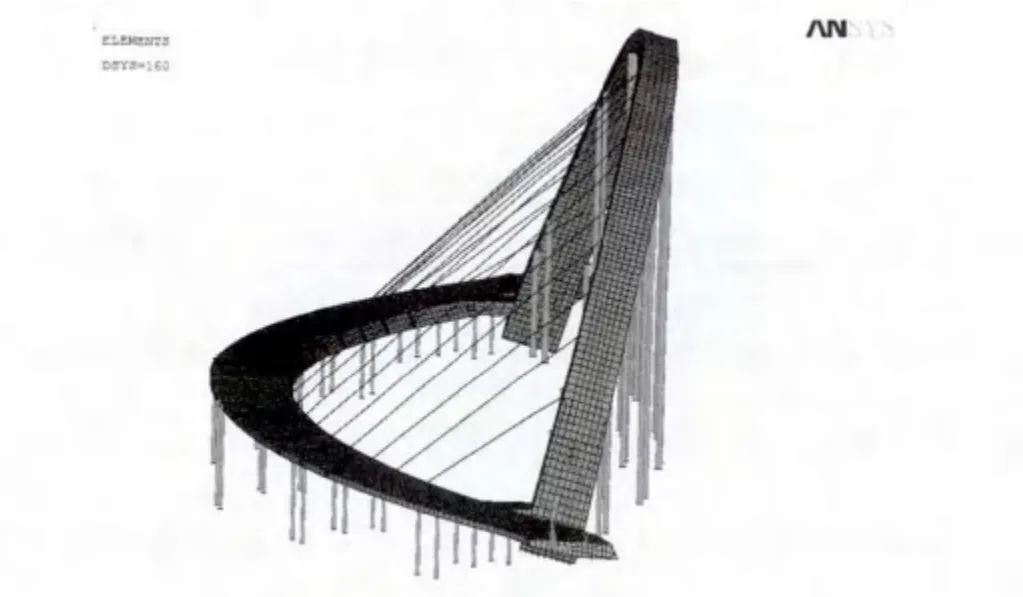
圖3 一干河斜拱橋Ansys 模型Fig.3 Ansys model of the Yigan river cable arch bridge

2)吊桿張拉次序按施工逆序進行計算。本橋吊桿施工張拉順序為先中間(拱頂)后兩邊(拱腳)對稱進行。按照施工方案吊桿張拉順序的逆過程依次“殺死”相應的吊桿，從而獲得當前狀態下后續“殺死”吊索的張拉力。與該張拉力對應的就是按照橋梁的施工方案進行到當前狀態時應當施加的吊桿初拉力［6］。

3)根據上述求得的吊桿張拉力對橋梁結構進行正序分析，判斷所得的計算狀態是否與步驟1)的既定狀態吻合，如果不一致則仍需進行迭代計算，與此同時需對各施工階段結構的安全性進行分析。

2.2.2 倒裝計算法運算應用 根據設計方提供的成橋索力，利用倒裝法依次逆向推導出鋪裝階段的索力、實現橋面系脫架工作對應的索力以及拱肋脫架后的索力(模型計算中可通過改變結構對應階段的自重來實現這一目標)，如表1 所示;并且運用倒裝法確定了初張拉時各吊桿的張拉力來實現橋面系脫架這一重要施工環節。

表1 施工各階段對應的索力理論計算值Tab.1 Calculated value of the cable force in theory

3 影響矩陣法控制張拉力的計算

3.1 影響矩陣法運算步驟

影響矩陣法的基本運算式表述為

式中:［F10F20… Fn0］T為吊桿的初始索力［F1F2…Fn］T為吊桿的目標索力;［Δx1Δx2… Δxn］T為張拉力增加值(基本未知量);tij為第j 號吊桿增加單位力時對i 號吊桿的影響，將這些系數組裝后得到影響矩陣;n 為吊桿組數。

對于再張拉的情況，影響矩陣滿秩，即式(1)存在唯一解。通過解線性方程組，可以得到［Δx1Δx2…Δxn］T，進而按下式求得施工張拉力［x1x2…xn］T:

上述方法基于一個重要的前提條件:所有的吊桿在張拉過程中都參與作用，即不存在壓力松弛而退出工作的現象［8］。如果在理想的假定基礎上求解的施工力使其他吊桿產生松弛時，把該松弛吊桿在計算模型中拆除，等到張拉該吊桿時，才將其加入到幾何模型中，形成新的影響矩陣，再按式(1)計算張拉力。

如此循環，直到所有的吊桿都不存在松弛現象。影響矩陣法多用于處在線性狀態的結構，且結構體系、約束情況保持不變，而對于結構體系不斷變化的初張拉(橋面系未脫架)情況并不適合。

3.2 影響矩陣法計算吊桿張拉控制力

待橋面系護欄安裝及混凝土澆筑作業完成后，通過索力測試儀測出DS1至DS10(10＇)的索力分別為173.9 kN，178.0 kN，172.5 kN，173.3 kN，156.7 kN，160.2 kN，183.0 kN，212.5 kN，192.8 kN，209.4 kN。對照吊桿張拉力的設計值，采用2 臺千斤頂由中間到兩端對稱張拉，以消除索力差值。張拉順序為:DS1→DS2;DS2'→DS3;DS3→DS3'→DS4;DS4'→DS5;DS5'→DS6;DS6'→DS7;DS7'→DS8;DS8'→DS9;DS9'→DS10;DS10'。

3.3 原始剛度矩陣的建立

首先建立處于上述索力的原始計算模型，然后按照上述張拉順序對吊桿進行張拉，每次張拉后恢復原始模型，再張拉下一對吊桿。在具體操作計算中，將張拉力的增量設定為20 kN，然后將矩陣每個元素除以20，由此可得到影響矩陣各系數見表2所示。

表2 初始影響矩陣系數Tab.2 Initial influence matrix coefficients

根據索力實測值［F10F20…F100］T= ［173.9 178.0 172.5 173.3 156.7 160.2 183.0 212.5 192.8 209.4］T;索 力 控 制 值［F1F2…F10］T= ［209.0 205.0 193.0 204.0 183.0 181.0 194.0 202.0 196.0 215.0］T;按照式(1)，利用Matlab 語言按Jabobi 迭代算法求解此10 階線性方程組，初步計算結果為［Δx1Δx2…Δxn］T= ［598.2 501.6 530.7 532.5 504.9 446.9 385.7 297.4 245.3 168.9］T。為了滿足吊桿在張拉過程中都參與作用的重要條件，檢驗Δxi(i = 1，2，…n －1)，若則令i = i +1 繼續進行檢驗，直到全部滿足條件;相反，若得到，則需令Fi，0=0，ti+1，1= 0，ti+1，2= 0 …ti +1，i = 0 代入方程組重新計算［Δx1Δx2…Δxn］T。

經過多次修正后最后影響矩陣系數修正如表3所示。

表3 修正后影響矩陣系數Tab.3 Modified influence matrix coefficients

代入式(1)重新計算求得各吊桿張拉力增加值［Δx1Δx2…Δxn］T= ［375.9 312.5 326.7 316.1 277.3 254.8 227.8 168.0 142.1 98.9］T，然后根據式(2)求得實際張拉過程中各吊桿的張拉力［x1x2…xn］T= ［549.8 421.2 341.7 316.1 277.3 254.8 245.5 233.8 208.7 215.0］T。

按上述計算所得索力和張拉順序張拉吊桿，最終所得索力實測值與設計值對比結果如表4 所示。

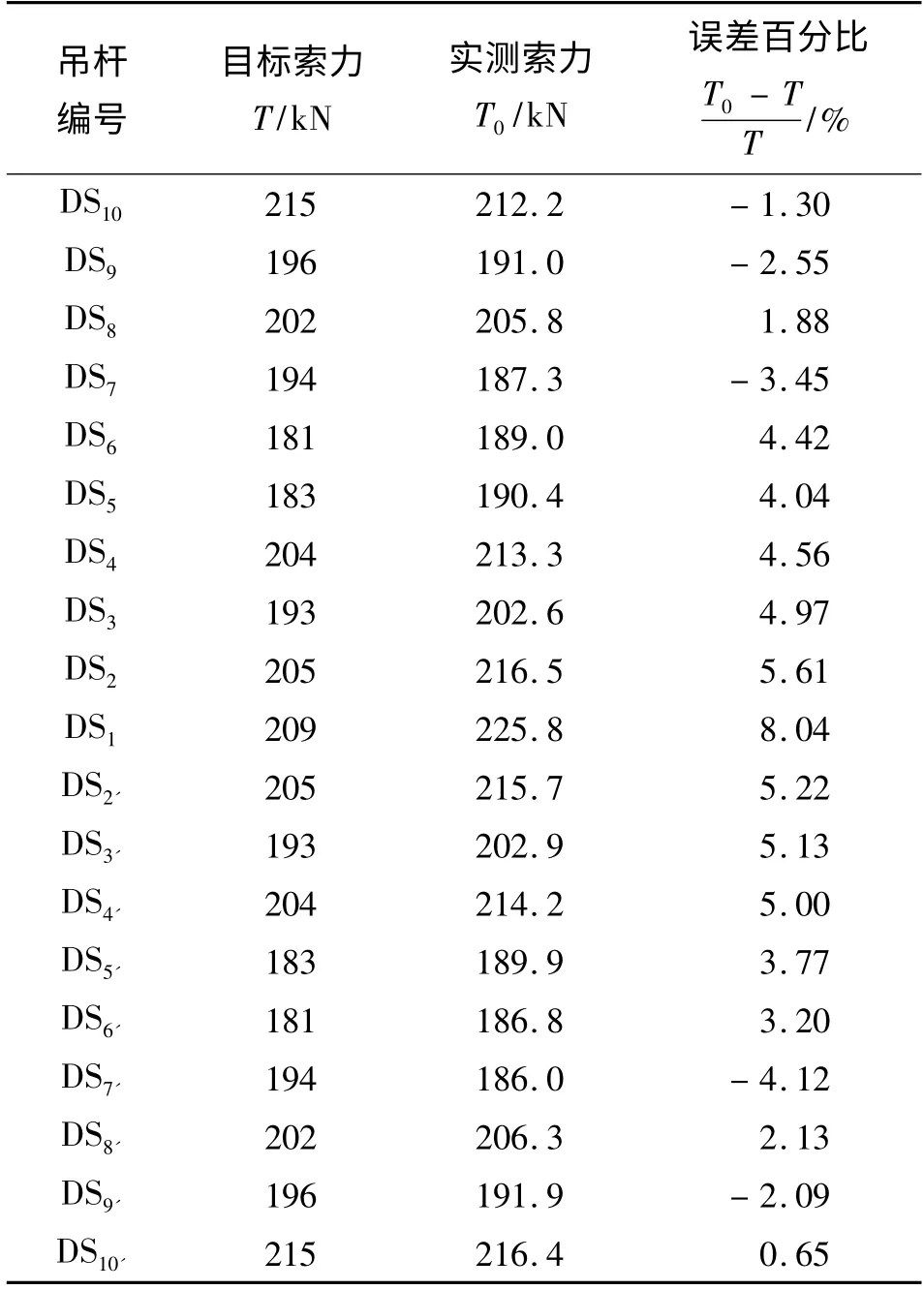
表4 張拉力結果對比Tab.4 Results comparison of tensile force

從表4 數據可以看出，成橋狀態的實測索力和目標索力最大差值出現在首次張拉的DS1位置，末次張拉的D10、DS10'索力和設計值最為接近，因為后期張拉的吊桿會對前期已完成張拉的吊桿產生影響;最大誤差百分數為8.04 ＜10，滿足相關技術的要求。

4 結 語

以一干河上修建的大跨度鋼箱梁斜拱橋為例，分別利用Ansys 與Matlab 軟件，采用倒裝法與影響矩陣法分別計算了吊桿在不同工況下的張拉力。在倒裝法中，利用軟件的“生死單元”高級技術依次逆向推導出鋪裝階段的索力、橋面系脫架工作階段的索力以及拱肋脫架后的索力，配合施工方完成了吊桿的初張拉及橋面系主梁的脫架工作。

橋面護欄安裝和混凝土澆筑作業完成后，利用DH5906 無線索力測試儀采取振動頻率量測法進行索力監測，根據索力實測值與設計值間的差異，利用影響矩陣法，通過簡單的回代方法求出施工過程中每根吊桿對應張拉順序的控制值，從而對吊桿張拉力進行實際控制，并最終完成成橋階段的調索工作。

在吊桿張拉控制方面，利用倒裝法和影響矩陣法的分析結果實時監控，大大縮短了施工時間，節省了施工費用，為此橋安全順利的施工提供了可靠的技術支撐。

［1］孫九春.拱式結構吊桿張拉索力計算方法綜述［J］.結構工程師，2010，26(4):154-159.

SUN Jiuchun.Calculation method of cable force of arch structure［J］.Structural Engineer，2010，26(4):154-159.(in Chinese)

［2］楊俊.基于影響矩陣的大跨橋梁合理成橋狀態與施工控制研究［D］.武漢:武漢理工大學，2008.

［3］劉智芳.臺風區大跨度鋼桁架拱橋施工控制關鍵技術研究［D］.廣州:華南理工大學，2014.

［4］李洪波，馬玉全，于天龍.基于影響矩陣的系桿拱橋合理成橋吊桿索力確定［J］.科學技術與工程，2009(10):17-19.

LI Hongbo，MA Yuquan，YU Tianlong.Determination of rational completion hanger force of bowstring arch bridges on the basis of influence matrix method［J］.Science and Technology and Engineering，2009(10):17-19.(in Chinese)

［5］李歡，朱召泉，朱瑞虎.某大跨度斜拱橋施工仿真分析與對比［J］.低溫建筑技術，2014，36(10):88-91.LI Huan，ZHU Zhaoquan，ZHU Ruihu.Construction simulation analysis and comparison of a large span obligue arch bridge［J］.Low Temperature Architecture Technology，2014，36(10):88-91.(in Chinese)

［6］李新平，鐘健聰.空間系桿拱橋吊桿張拉控制分析［J］.華南理工大學學報:自然科學版，2004，32(7):89-92.

LI Xinping，ZHONG Jiancong. Control analysis of the tension in suspenders of a spatial tied-arch bridge［J］. Journal of South China University of Technology:Natural Science Edition，2004，32(7):89-92.(in Chinese)

［7］鐘健聰，李新平.空間系桿拱橋吊桿張拉控制的研究I［J］.廣東公路交通，2004(2):1-4.ZHONG Jiancong，LI Xinping. Research on control of tensions in suspenders for a spatial tied-arch bridge［J］. Guangdong Highway Communications，2004(2):1-4.(in Chinese)

［8］孫九春.影響矩陣法在吊桿張拉計算中的應用［J］.中國市政工程，2009(5):19-21.

SUN Jiuchun.On influence matrix method applied in the suspender tension computing［J］. China Municipal Engineering，2009(5):19-21.(in Chinese)