非自治F-N 系統(tǒng)在帶參數(shù)的空間中全局吸引子的存在性

周康寶， 李曉軍

(河海大學(xué) 理學(xué)院，江蘇 南京210098)

1 預(yù)備知識

考慮Ω ?Rn為有界光滑區(qū)域，考慮下面非自治方程:

初值條件和邊界條件為

其中a，λ，b 是非負(fù)常數(shù)，f ∈L2(Ω)，g ∈L2(Ω)。h 是一個非線性光滑函數(shù)，且滿足

且存在L ＞0，使得

當(dāng)ε(t )是不依賴于時間t 的常數(shù)時，在文獻(xiàn)［1］中作者研究了式(1.1)～(1.4)全局吸引子的存在性。考查系統(tǒng)(1.1)～(1.4)中ε(t)與時間t有關(guān)，且由于ε(t)在無窮遠(yuǎn)處衰減為0，因而具有奇異性，主要源于系統(tǒng)(1.2)變?yōu)楸Ｊ叵到y(tǒng)。這在運(yùn)用經(jīng)典的方法得到吸收集的存在性時帶來一定的困難，為得到時間導(dǎo)數(shù)項(xiàng)或-Δ 項(xiàng)依賴于時間參數(shù)的波方程的全局吸引子的存在性，作者分別在文獻(xiàn)［2］中將時間參數(shù)并入過程所定義的空間，給出在依賴于參數(shù)t 的空間中全局吸引子的存在性。文中應(yīng)用文獻(xiàn)［3］中的理論，考查系統(tǒng)(1.1)～(1.4)依賴于時間t 的全局吸引子的存在性。

首先給出關(guān)于含參數(shù)的空間的一些概念對于每個對t ∈R，令Xt是一族依賴于t 的賦范空間，稱雙參數(shù)映射U(t，τ):Xτ→Xt是一個過程，若它滿足:

1)U(t，τ)= U(t，r)U(r，τ)，?τ ≤r ≤t;2)U(τ，τ)是Xτ上的恒同映射。

令Bt(R) = {z ∈Xt:‖z‖Xt≤R}，設(shè)A，B 的Hausdorff 半距離為

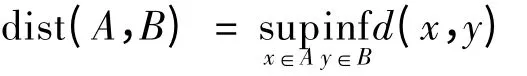
若對任意的t ∈R，存在Rt，使得Ct?Bt(Rt)成立，則稱集族C = {Ct}t∈R在Xt中是有界的。

定義1.1 稱有界的一族集合{Bt}t∈R是拉回吸收集，如果對任意的R ＞0，都存在t0= t0(t，R)≤t，使得

稱過程U(t，τ)是耗散的，若其擁有一拉回吸收集。定義1.2 稱集族{Kt}t∈R，Kt?Xt，是拉回吸引的，若對任意的ε ＞0，集族{(Kt)}t∈R是拉回吸收的，其中(Kt)是Kt在Xt中的ε-鄰域。若過程U(t，τ)擁有一個非空緊的拉回吸引集，即{Kt}t∈R是拉回吸引的，Kt?Xt是Xt中的緊集，則稱U(t，τ)是漸近緊的。

定義1.3 稱{At}t∈R是過程U(t，τ)依賴于時間的全局吸引子，如果{At}t∈R是拉回吸引的，At?Xt是緊集。

為保證吸引子的不變特性，引入下面定義。定義1.4 稱U(t，τ):Xτ→Xt是閉的，若對任意給定的則有U(t，τ)x = ξ。

若對固定的T ＞0，U(t，t － T)是閉的，則稱U(t，τ)是T-閉的。

由上述定義可知，連續(xù)過程，強(qiáng)弱連續(xù)過程，閉過程都是T-閉的。下面給出關(guān)于依賴時間的全局吸引子存在性的抽象結(jié)果，證明如同文獻(xiàn)［4-6］。

定理1.1 假定過程U(t，τ):Xτ→Xt是漸近緊的，則存在依賴于時間的全局吸引子{At}t∈R，At?Xt，進(jìn)一步假設(shè)U(t，τ)是T-閉的，則{At}t∈R滿足不變特性:U(t，τ)Aτ= At，t ≥τ，τ ∈R。

注 上定理給出的全局吸引子沒有唯一性，若過程U(t，τ)擁有一個一致有界的緊的拉回吸收集，則定理1.1 中所描述的全局吸引子在吸引意義下是唯一的。

2 主要結(jié)果

對于系統(tǒng)(1.1)～(1.4)，令含參量空間Xt:=L2(Ω)×L2(Ω)，令‖·‖表示L2(Ω)范數(shù)，定義空間Xt的范數(shù)為

同理，定義空間Yt= H2(Ω)×(Ω)，范數(shù)為

由ε(t)的假設(shè)可知，空間Xt與Xτ等價，空間Yt與Yτ等價，當(dāng)t →+ ∞時，等價常數(shù)爆破。

由標(biāo)準(zhǔn)的Galerkin 方法如見文獻(xiàn)［7-9］，有如下結(jié)果。

定理2.1 假設(shè)式(1.5)～(1.8)成立，那么問題(1.1)～(1.4)在L2(Ω)× L2(Ω)中適定，即對任意的τ ∈R，任意的初值(uτ，vτ)∈L2(Ω)×L2(Ω)，和任意的T ≥0，方程(1.1)～(1.4)存在唯一的弱解(u，v)∈C(［τ，t］;L2(Ω)×L2(Ω))，且該解連續(xù)地依賴于初值。

由上述定理可知，在Xt中可以定義過程U(t，τ):

其中(u(t)，v(t))是系統(tǒng)(1.1)～(1.4)的解。引理2.1 假設(shè)系統(tǒng)(1.1)～(1.4)成立，則對Xτ中的任何有界集B = Bτ(R)，存在τ0= τ0(B，t)，使得，對式(1.1)兩邊用ε(t)u 在L2(Ω)中作內(nèi)積，得到

證 令

對式(1.2)兩邊用v 在L2(Ω)中作內(nèi)積，得到

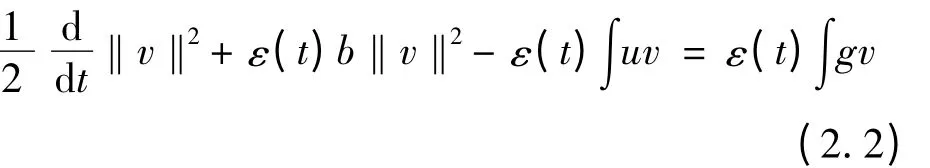
將式(2.1)和式(2.2)相加，并應(yīng)用ε(t)的假設(shè)可得

式(2.3)右邊兩項(xiàng)可以估計(jì)為

應(yīng)用式(1.7)～(1.8)，由于式(2.3)～(2.5)可以得到

由上式可得

忽略式(2.6)中左邊第3 項(xiàng)，對式(2.6)應(yīng)用Gronwall 引理可得

由上式可知，當(dāng)τ →－ ∞時，有

由引理2.1 可知，過程U(t，τ)存在一個有界的拉回吸收集{Bt}t∈R，其中

引理2.2 假設(shè)式(1.5)～(1.8)成立，則對任意的(uτ，vτ)∈Bτ，存在τ0= τ0(t，Bτ0)，使得

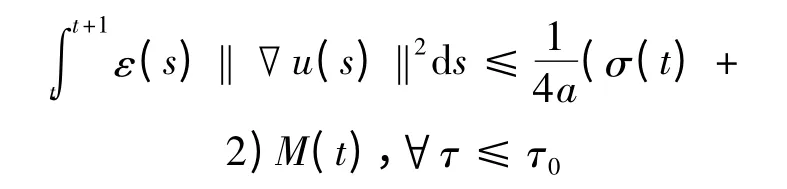
證 對式(2.6)兩邊在(t，t +1)積分，并應(yīng)用引理2.1 可得

引理2.3 假設(shè)式(1.5)～(1.8)成立，則對任意的(uτ，vτ)∈Bτ，存在τ0= τ0(t，Bτ0)，使得

證 用－ε(t)Δu 對(1.1)在L2(Ω)中做內(nèi)積可得

上式右邊最后一項(xiàng)可估計(jì)為

對于式(2.8)右邊第2 項(xiàng)，有以下估計(jì):

由式(1.5)～(1.6)可得

此處C 是式(1.5)中的常數(shù)。由式(2.8)～(2.11)并應(yīng)用ε(t)的假設(shè)可得

結(jié)合引理2.2，對式(2.12)利用一致Gronwall 引理可得

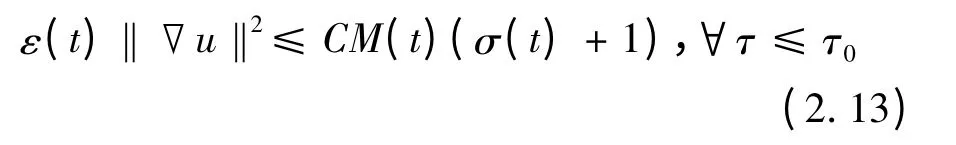
為了估計(jì)v 的漸近緊性，需要對v 進(jìn)行分解:v =v1+ v2，其中v1和v2分別滿足

易知，v1滿足

故有當(dāng)τ →－ ∞時，‖v1‖→0。

下面給出v2在H1(Ω)中的正則性。引理2.4 假設(shè)式(1.5)～(1.8)成立，則對任意的(uτ，vτ)∈Bτ，有

證 對式(2.15)兩邊用－Δv2在L2(Ω)中作內(nèi)積，可得

式(2.16)右邊第一項(xiàng)可估計(jì)為

從式(2.16)右邊第2 項(xiàng)可估計(jì)為

那么從式(2.16)～(2.18)可得

結(jié)合引理2.3，對式(2.19)利用Gronwall 引理可得

由上式可知，當(dāng)τ →－ ∞時，有

定理2.2 假設(shè)公式(1.5)～(1.8)成立，則公式(1.1)～(1.4)所對應(yīng)的過程在Xt中有依賴于時間的全局吸引子{At}存在。

證 由引理2.1 可得過程在Xt中有一個依賴于時間的吸收集。由引理2.2 ～2.4 可得系統(tǒng)所對應(yīng)的過程在Xt中是漸近緊的。利用定理2.1 及定理1.1，可以得到過程在Xt中有依賴于時間的全局吸引子{At}存在。

［1］WANG B X.Attractors for the non-autonomous FitzHugh-Nagumo systemn on unbounded domains［J］.Nonlinear Anal，2009，70:3799-3915.

［2］Comti M，Pata V，Temam R.Atrractor for processes on time-dependent spaces.applications to wave equations［J］.J Differential Equations，2013，255(6):1254-1277.

［3］Plinio F DI，Duane G S，Temam R. Time dependent attractor for the oscillon equation［J］. Discrete Contin Dyn Syst，2011，29(1):141-167.

［4］Garca-Luengo J，Marn-Rubio P，Real J. Pullback attractors in V for non-autonomous 2D-Navier-Stokes equations and their tempered behavior［J］.J Differential Equations，2012，252:4333-4356.

［5］Marn-Rubio P，Real J. On the relation of between two different concepts of pullback attractors for non-autonomous dynamical systems［J］.Nonlinear Anal，2009，71:3956-3963.

［6］Caraballo T，Lukaszewicz G，Real J. Pullback attractors for asymptotically compact non-autonomous dynamical systems［J］.Nonlinear Anal，2006，64:484-498.

［7］Robin J C. Infinite-Dimensional Dynamical Systems An Introduction to Dissiptative Parabolic PDEs and the Theory of Global Attractors［M］.Cambridgeshire，England:Cambridge University Press，2001.

［8］Temam R.Infinite-Dimensional Dynamical Systems in Mechanics and Physics［M］.New York:Springer，1997.

［9］ZHANG Y，ZHONG C，WANG S.Attractors in L2(RN)for a class of reaction-diffusion equations［J］.Nonlinear Anal，2009，71:1901-1908.