淺談高等數學教學中數學建模思想的滲透

吳志強

（甘肅畜牧工程職業技術學院 甘肅 733006）

淺談高等數學教學中數學建模思想的滲透

吳志強

（甘肅畜牧工程職業技術學院 甘肅 733006）

隨著科學技術進步和社會發展的日新月異，高職院校的數學教學也順應時代發展需求進行了諸多方面的改革探索：淡化理論體系的推導與復雜的計算，強化數學概念的建立及數學的實踐性、應用性；在數學教學中引入數學建模的內容，把數學和實際應用問題聯系起來等。其中，數學建模思想的滲人極大地促進了高職院校數學教學的改革與創新，進而達到提高教學和科研能力的效果。

雖然高等數學課程本身的內容多，課時不夠，但我們將數學建模的思想融入高等數學課程中，并不是用“數學建模”課的內容搶占高等數學課程的課時，在此，僅從兩個方面將數學建模的思想逐步滲透到高等數學的教學中。

一、在高等數學的概念中融入數學建模的思想

從廣義上講，高等數學教材中的導數、定積分等復雜抽象的概念都來源于實際。因此在講授這些概念時可以恰當選取一些生動的實例來吸引學生的注意力，同時將概念模型自然地建立起來，使學生充分感受到實際問題向數學的轉化。為了在概念的引入中展現數學建模，首先必須提出具有實際背景的引例。下面我們就以高等數學中導數這一概念為例加以說明。

引例：變速直線運動的瞬時速度

1。提出問題：設有一物體在作變速直線運動，如何求它在任一時刻的瞬時速度？

2。建立模型：物體沿直線的運動可理想化為質點在數軸上的運動。假設質點在t=0時刻位于數軸的原點，在任意的時刻t，質點在數軸上的坐標為s=s(t)。下面討論質點在時刻的瞬時速度即：已知質點的運動方程s=s(t)，求瞬時速度

質點從t0到這段時間間隔內通過的路程為

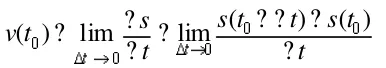
上式即為己知物體運動的位移函數s=s（t），求物體運動到任一時刻t0時的瞬時速度的數學模型。這個模型,我們拋開它的實際意義單從數學結構上看，可歸結為一個數學模型，即求函數改變量與自變量改變量比值，當自變量改變量趨近于零時的極限值。由此,我們引入函數的導數定義

定義設函數y=f（x）在點x0的某個鄰域內有定義，當自變量x在點x0處取得改變量△x(x0+△x仍在該鄰域內△x≠0，且)時，相應的函數改變量

存在，則稱函數y=f(x)在點x0可導，并稱此極限值為函數y=f(x)在點x0處的導數，記作

二、在高職高等數學教學中,將數學建模案例與定理講解相結合

例如,在介紹條件極值的時候,可以與“奶制品的生產與銷售”這個建模例子結合起來講解,通過教師的引導,將條件極值和這個問題聯系起來,找到它們之間的關系,用數學建模的思想解決這個實際問題。在講解極值定理時,可以增加簡單的優化模型,例如與“存貯模型”“生豬出售時機”“最優價格”等數學模型相結合。通過這些實際問題的模型,學生能更好理解高等數學中定理,并學會應用定理解決實際問題。

三、在高等數學習題課教學中可以增加建模案例教學的環節

數學建模案例的難易程度應與高職學生的知識水平和學習能力相符,過于簡單或過于困難都不利培養學生的學習興趣,要選取難易適當、與現實生活相關的實際問題,例如,在微分中值定理及導數應用這一章習題課中可以增加“消費者選擇”數學模型;在積分知識及其應用這一章習題課中可以增加“存儲問題”數學模型等等。通過對這些與現實相關的問題的研究,學生能清楚地認識到高等數學在實際問題中的應用,從而積極主動地應用數學知識分析問題、解決問題。

四、在高等數學課程的考核中增加數學建模問題

學完每章節的內容后,在課外作業的布置中,除書本中的習題外可以再增加一兩道需要運用本章知識解決的實際問題的數學建模題目,這些數學建模可以讓學生獨立或自由組合成小組去完成,給予完成情況好的學生較高的平時分,在期末考試試題中以附加題的形式增加數學建模的題目。用這種方法,鼓勵學生應用數學的知識解決現實中各種問題,提高學生使用數學知識解題的能力,調動學生的學習積極性,從而使學生獲得除數學知識本身以外的素質與創新能力。

在高等數學教學中融入數學建模思想,培養學生的建模能力,是符合當代人才培養要求的,是可行的。數學建模思想的融入要采用漸進的方式,盡量與已有的教學內容進行有機的結合。實踐證明,通過在高等數學教學中融入數學建模思想,不僅激發了學生的學習興趣,培養了學生的創新能力,還可以促進教師進行自我提升。但如何在高等數學教學中很好地融入數學建模思想目前還處于探索階段,仍需要廣大數學教師的共同努力。