智能BIT降虛警技術

孫金明，潘紅兵，周晶晶

（海軍工程大學 湖北 武漢 430033）

機內測試（Built-in Test，簡稱BIT）是系統或設備自身為故障檢測、隔離或診斷提供的自動測試能力。它是一種能顯著改善裝備或系統測試性能與診斷能力的重要技術手段，在航空電子設備可靠性與維護性設計中日益受到重視。但虛警率較高始終是困擾BIT技術研究和應用的主要問題之一。BIT虛警問題是導致武器系統戰備完好性差、使用保障費用高的重要因素。虛警率高不但直接影響BIT的有效性，而且對武器系統的戰備狀態產生種種不利影響。

1 BIT虛警原因分析

產生BIT虛警的原因大致可歸納為以下9種：設計者的假設不當[1]；BIT設計不適合系統的實際情況；測試門限值/容差不合理；BIT或其他監測電路失效；錯誤的故障隔離；正常系統的偶然故障或偶然的性能變化；不適當激勵或干擾；時間環境應力；間歇故障的影響等[2]。其中最主要的是:

1）時間環境應力:根據美軍ROME空軍實驗室的研究報告，時間環境應力是造成現役電子設備BIT虛警的重要原因。由美軍機載電子設備環境應力故障原因比率圖 （如圖1所示）可知:50%以上的電子設備故障是由各種環境因素引起的，其中溫度、濕度、振動三項就造成大約44%的故障。惡劣的環境因素使電子系統在實際工作條件下所承受的環境應力與原來預計的不同，使得系統工作特性與原計劃相比發生了變化，這樣就直接影響到BIT模塊本身，造成原設計的BIT特性出現虛警區和未檢測區，使BIT有效性下降，而產生虛警。

2）間歇故障:根據美軍裝備和電子工業的數據表明:間歇故障是產生BIT虛警的一個主要原因，占電子系統BIT虛警的30%～40%。間歇故障的特點是隨機出現和消失，其發生時間很隨機，在有限的、不能預料的時間內對系統產生影響，且沒有明顯的模式或頻率。

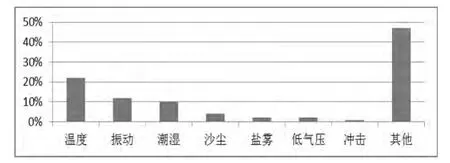
圖1 機載電子設備環境應力故障原因比較Fig.1 Comparison of airborne electronic equipment malfunction causes of environmental stress

間歇故障的這種不確定性引起了BIT診斷的不確定，表現出如圖2所示的各種現象。圖中，INTERMITTENT是間歇故障，而 CND （不能復現）、NPF（沒找到問題）、NFF（沒找到故障）、RTOK （重檢合格）、NEOF （失效無法驗證）和ER（錯誤拆卸）是由間歇故障引發的不確定性問題，這些問題都因為報告了異常而事后卻找不到故障，于是導致虛警。

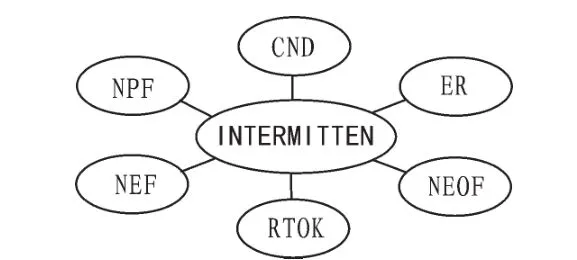
圖2 間歇故障導致的現象Fig.2 Phenomenon caused by intermittent faults

2 BIT的虛警控制

為解決以上問題達到提高BIT故障診斷能力、降低BIT虛警率的目的，分別從時間環境應力和間歇故障的角度出發，降低 BIT虛警[3]。

2.1 時間環境應力與BIT虛警分析

基于多元Logistic[4]回歸的關聯分析：

基于logistic分布的logistic回歸模型是對二分類因變量進行定量分析的有力工具，該方法在醫藥衛生社會科學領域廣泛應用于變量對結果的影響因素及重要程度計算。通過采用多元logistic回歸對時間應力和BIT虛警關聯分析進行定量分析，得到相應影響程度。

定義時間環境應力表達式如下：

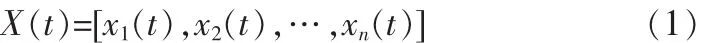
x1（t）為時間應力向量；xn（t）為某種應力參數，如振動，溫度等，xn（t）是一個隨機變量。

定義函數 y（t）為系統 BIT輸出，其中，0為正常狀態，1為虛警狀態，定義環境時間應力作用下系統發生虛警概率為：P（y（t）=1|X）=π（x）=π[x1（t），x2（t），…，xn（t）]

由logistic回歸模型理論，可以建立時間應力與BIT虛警關聯的多元logistic回歸模型為

式中，β0表示與各種應力因素無關的常數項，在數學模型中表現為回歸截距；βi為該回歸模型的回歸系數，具體表示各種應力因素，xn（t）導致BIT虛警的貢獻量，即各種應力因素對該虛警的影響程度。

通過環境時間應力與BIT性能影響分析，可知關聯閾值是影響時間應力與虛警關聯后BIT檢測率和虛警率的最要影響參數，這兩個閾值如果選擇不當，會導致降低BIT虛警識別效果，降低BIT檢測率。目前解決這類問題主要有Bayes理論，神經網絡、k近鄰方法、SVM等。SVM具有以下優點：1）結構簡單，各種技術性能泛化能力明顯提高。2）樣本較小情況下有很好的分類效果。3）算法確定的網絡結構是自動生成的，對模型選擇依賴度低。

2.2 間歇故障與BIT虛警分析

來自美軍裝備和電子工業的數據表明：間歇故障是導致系統暫時失效的一個主要原因，它占了整個系統故障的70%～90%，間歇故障[6]也是產生BIT虛警的一個主要原因，電子系統的虛警中有30%～40%是由間歇故障引起的。對此，美國相關研究機構開展了診斷間歇故障抑制BIT虛警的技術研究，通過診斷間歇故障，達到抑制虛警的目的。間歇故障和故障一樣是很多系統難以避免的問題，由于間歇故障情況復雜、時隱時現、難以診斷，因此基于兩狀態分類的傳統BIT一般是忽略或干脆避開間歇故障。由此產生的結果是:在間歇故障活躍時，BIT報警有永久故障，可事后又找不到故障，造成虛警率升高；在間歇故障不活躍時，BIT判斷系統為正常，造成間歇故障的漏診，使得故障檢測率降低。因此兩狀態分類就成為傳統BIT的一個最大的不足。

間歇故障時有時無，是一種變化劇烈的動態時間序列。傳統BIT的診斷方法多從單一時刻的狀態來判別 （如神經網絡虛警過濾器等），遺漏了系統的動態信息，易引起診斷決策的錯誤，從而導致BIT虛警。實際上，間歇故障前后時刻的態存在著一定的轉移關系，這種狀態轉移關系給診斷決策提供了重要的信息，如果有效地利用這些信息，則可以更準確地識別間歇故障。

HMM[6]是在Markov鏈的基礎上發展而來的一種統計模型，是一個雙重隨機過程。模型中真實的狀態不能直接看到，只能是通過一個觀測值去感知狀態的存在及特征。HMM具體可表示為 λ=（π，A，B）， 其中:π 為初始概率分布矢量；A為狀態轉移概率矩陣；B為觀測值概率矩陣。π，A描述的是一個Markov鏈，產生的輸出是狀態序列；B描述是一個隨機過程，產生的輸出為觀察值序列。模型采用左右型三狀態轉移的Markov鏈，每個狀態的觀測概率由2個高斯概率密度函數聯合決定。系統開始時總是處于正常狀態，因此取初始狀態概率矢量為π=[1，0，0]，A的初值均勻選取。為增加HMM診斷模型的穩健性，訓練時利用多個觀測值序列的重估算法，由初始模型對訓練樣本進行Baum-Welch算法：

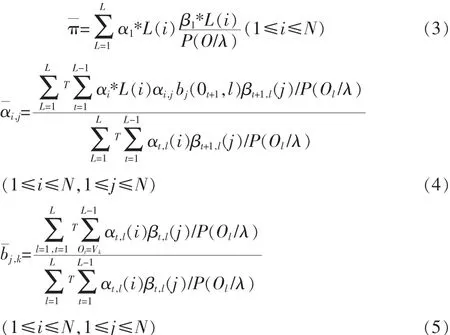
其中:α為前向變量；β為后向變量；L為觀測值序列的數量。由初始模型對訓練樣本進行匹配計算和狀態標注后，估計出一組新的模型，再對訓練樣本重新進行匹配計算和狀態標注，估計出更新的模型參數λ，如此反復直至收斂，得到優化模型，使P（O，λ）最大。診斷分為兩個階段：1）分別對正常、間歇和故障3種狀態的訓練樣本提取特征向量，利用Baum-Welch算法進行模型訓練，獲得各類典型故障的HMM模型；2）在實際狀態監測時，將測得的信號經EMD分解處理提取特征向量后作為觀測值序列，將其送入已經訓練好的HMM模型，通過前向-后向算法計算觀測向量在不同模型下的概率P（O，λ），由概率值最大的HMM模型決定被測系統的狀態。

3 結束語

虛警率較高始終是制約BIT技術研究和應用的瓶頸問題之一。本文從降低智能BIT虛警率入手，從時間環境應力和間歇故障角度，利用支持向量機（SVM）解決時間環境應力問題，利用隱馬爾科夫模型（HMM）解決間歇故障問題，有效的降低BIT虛警率。

[1]楊鈺.機內測試虛警分析和控制[J].新工藝新技術新設備，2007， 34（10）:93-96.YANG Yu.The analysis of false alarm in test and control[J].New Technology New Technology and New Equipment，2007，34（10）:93-96.

[2]徐永成，溫熙森，易曉山.機內測試虛警原因的分析及其解決方案[J].振動、測試與診斷，2002，22（1）:38-42.XU Yong-cheng，WEN Xi-sen，YI Xiao-shan.The analysis and solutions of the reason of BIT false alarm[J].Vibration Testing and Diagnosis，2002，22（1）:38-42.

[3]鄭文榮，夏清濤.武器系統BIT的設計與應用[J].艦船電子工程，2012，32（12）:131-133.ZHEN Wen-rong，XIA Qing-tao.The design and application of BITweapon system[J].Ship Electronic Engineering，2012，32（12）:131-133.

[4]Gao R X，Suryavanshi A.BIT for intelligent system design and condition monitoring[J].IEEE Transactions on Instrumentation and Measurement，2002，51（5）:221-225.

[5]柳新民，邱靜，劉冠軍，等.診斷間歇故障降低BIT虛警[J].測試技術學報，2004，18（4）:53-55.LIU Xin-min，QIU Jing，LIU Guan-jun，et al.Intermittent fault diagnosis BIT reduce false alarms[J].Test and Measurement Technology，2004，18（4）:53-55.

[6]張超，馬存寶，宋東，等.隱馬爾科夫模型[J].計算機測量與控制，2007，24（5）:58-61.ZHANG Chao，MA Cun-bao，SONG Dong，et al.Hidden markov models[J].Computer Measurement&Control，2007，24（5）:58-61.