普立特懸索橋抖振響應時域分析

黃文鋒, 鄒孔慶,2, 孫建鵬, 王美芹

(1合肥工業大學，安徽 合肥 230009；2中鐵四局集團鋼結構有限公司，安徽 合肥 230022；3西安建筑科技大學，陜西 西安 710055)

普立特懸索橋位于云南省宣威市境內，橫跨深度近400m的普立大溝，是普宣公路全線關鍵控制性工程之一．設計采用主橋960 m的雙塔單跨懸索橋，主橋跨徑布置為166+628+166 m．主纜橫向布置兩根，主纜橫橋向中心間距為26 m．上部結構主橋采用628 m單跨簡支鋼箱加勁梁懸索橋，普立岸主墩塔高154.3 m，宣威岸主塔高162.2 m，主纜邊跨均為166 m，索塔采用直塔柱門式框架結構，基礎采用群樁基礎，普立岸采用隧道錨，宣威岸采用重力錨．下部結構采用等截面鋼筋混凝土矩形墩、群樁基礎，普立岸采用重力式橋臺，宣威岸采用肋板式橋臺，橋型布置如圖1所示．

圖1 普立特懸索橋橋型布置圖Fig.1 PLT suspension bridge

大跨度橋梁屬于輕柔結構．其風致振動會給過往車輛及行人安全帶來很大影響，容易引起橋梁結構局部構件的疲勞問題[1]，有必要對其風致抖振問題進行研究．橋梁在隨機風荷載作用下的響應計算主要包括頻域法和時域法兩類．頻域分析方法較為簡單，但其需要計入一定數量的模態，得到的響應值為數字特征，并且只能進行線性分析．而時域法一般將結構進行有限元法離散后進行時程分析，可以得到其各種響應的時程，計算結果較為清晰簡單，同時可以深入理解各種非線性因素對大跨度橋梁空氣動力特性的影響．國內外一些學者對大跨度橋梁結構非線性抖振時域分析都進行了較為深入的研究[2]．但時域分析的不足之處在于公式分析求解難度較大，采用數值分析需要較高的計算機內存，耗時．但隨著計算機技術的發展，這些問題基本上都可以解決，抖振響應時域分析法已經成為橋梁抗風設計研究的重要課題[3]．

進行時域分析的核心是得到荷載時程，因而抖振力的隨機模擬成為首先要解決的問題，目前采用的方法通常是根據已知的脈動風功率譜模擬得到對應的風速時程，再由準定常理論將風速轉化抖振力時程，編寫相應的循環加載抖振力數據的程序，并在ANSYS的MATRIX27單元加入氣動剛度矩陣和氣動阻尼矩陣考慮自激力作用[4]，最后利用ANSYS軟件循環讀入相應數據到橋梁結構節點上，求解動力方程，獲取橋梁時域內的抖振響應分析結果．本文對云南普立特大橋的抖振響應的時域分析采用了與上述相同的分析方法．

1 脈動風模擬

本研究借鑒 George Deodatis 的諧波合成法模擬了云南普立特大橋處的空間脈動風場[5,6]．在該橋梁有限元模型上共設置n個風荷載施加點，對應的形成 n維零均值平穩高斯隨機過程向量 f(t)，如下所示：

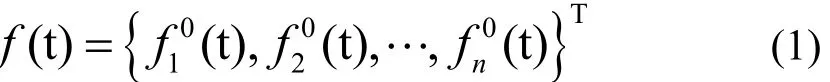
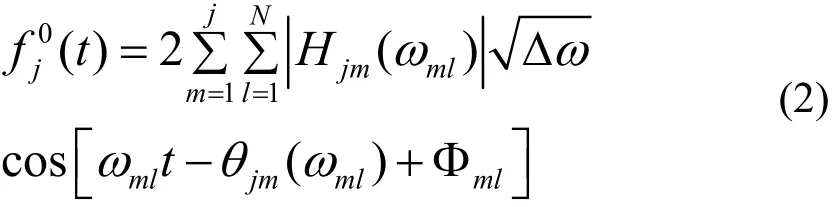
其中，N為充分大的正整數；Δω為頻率增量，等于ωup/N，ωup為截止圓頻率，當 ω＞ωup時，S0(ω)=0；Фml為均勻分布于[0,2π]區間的隨機相位角；Hjm(ωml)為矩陣 H(ω)正的元素，H(ω)是 S0(ω)的 Cholesky 分解，其中 S0(ω)、H(ω)如下式（3）及（4）所示；θjm(ωml)為 Hjm(ωml)的復角．

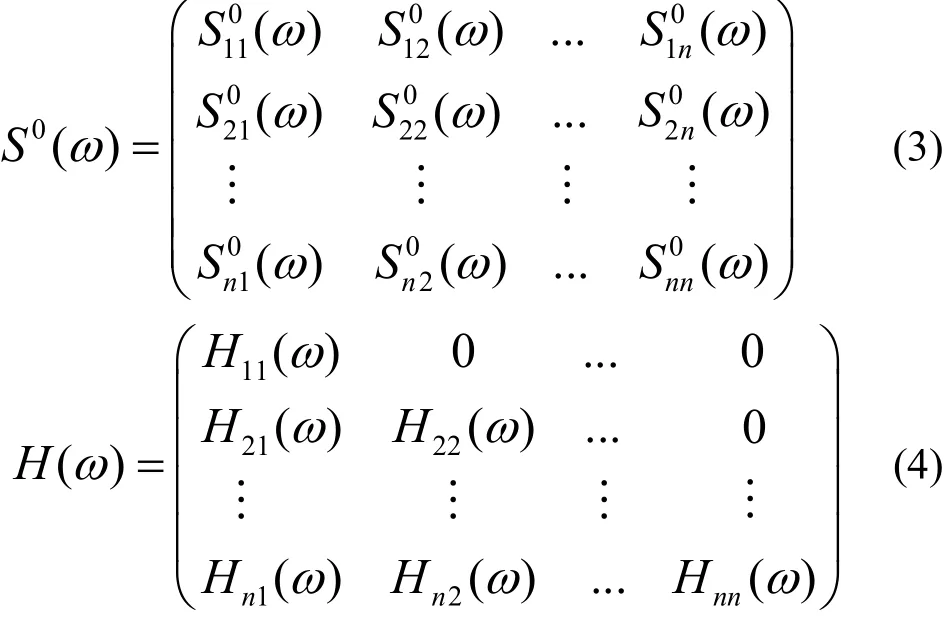
綜上所述，已知 S0(ω)，適當選擇 N、ωup、Δt就可以獲得好的隨機過程樣本；同時采用FFT（傅里葉變換技術）技術，大大提高了該類方法的計算效率.

針對大跨度橋梁而言，整個主梁基本處于同一高度，可近似認為沿主梁布置的n個模擬點具有相同的平均風速和水平脈動功率譜．

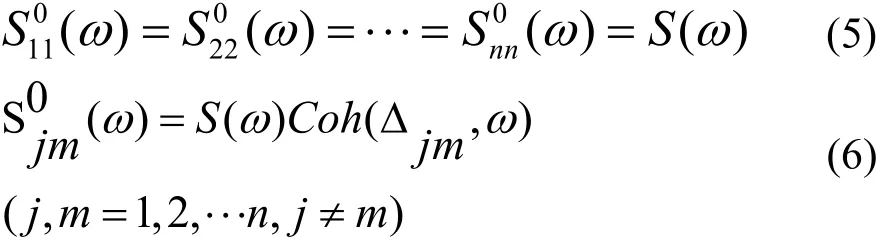
其中：Δjm為 j、m 兩點間距離；Coh(Δjm,ω)為相干函數．

考慮到橋面上模擬點為等間距布置(除主梁離橋墩較近的點，但距離相差不大)，間距為Δ，則有Coh(Δjm,ω)采用 Davenport相干函數.

對主塔而言自然風的風速正交譜很弱，一般可忽略，故沿主塔高度上各點的互功率譜表達式為(j≠m)：

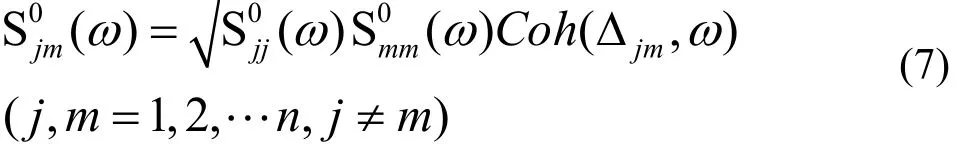
2 抖振力計算

模擬得到脈動風速時程后，就可將其轉化為作用于結構上的風荷載時程．通常將風致風荷載分為三部分：平均風引起的靜風力、脈動風引起的抖振力和氣動耦合產生的自激力，其中靜風力計算公式可參見文獻 [7]，自激力計算公式見下文，抖振力的計算公式參見文獻[8]，具體來說脈動風作用下橋梁單位展長的抖振力計算公式如下所示：

其中：Lb(t)、Db(t)、Mb(t)分別為在初始風軸坐標系下的氣動升力、阻力及扭矩；ρ為空氣密度；U為設計基準風速；B為橋梁主梁的計算寬度；u(t)、w(t)分別為順風向及垂直向脈動風速；CD、CL、CM和DC′、LC′、MC′分別為主梁初始風攻角方向上的氣動阻力、升力和扭矩系數及其導數．為便于在有限元中實現，常將抖振力轉換為節點坐標系下的節點集中力，采用集中法，將單元上的三分力堆積到節點上，以集中力的形式施加到有限元模型上，其風軸坐標系的抖振力的轉換節點坐標系關系如下所示：

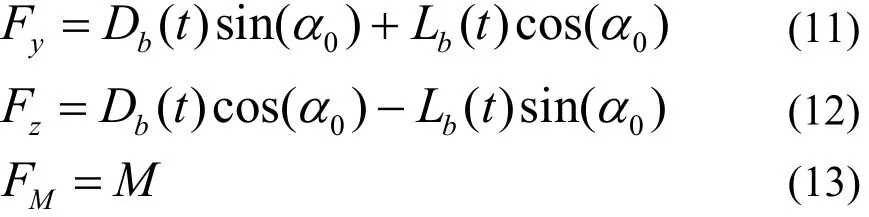
其中：Fy、Fz、FM分別為節點坐標系下的抖振力項，α0為初始風攻角.

對于主塔和橋墩，僅考慮其抖振阻力的作用，單位長度上的主塔抖振阻力的表達式為

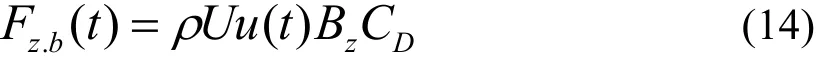
其中，Bz為橋塔和橋墩在迎風面的投影面積；CD為主塔的阻力系數．

為便于計算，通常將實際非線性的抖振力進行準定常假設下的線性化處理，忽略其中小量的耦合作用，雖然對結構計算精度有所影響，但對一般橋梁而言計算精度是滿足要求的．

3 自激力計算

自激力是風場和彈性體之間的相互作用．為方便在 ANSYS中實現，此處采用曾憲武等人在Miyat[9]準定常氣動模型基礎上，通過進行雙泰勒級數展開導出的 12階氣動剛度矩陣和氣動阻尼矩陣來表達自激力[10]．

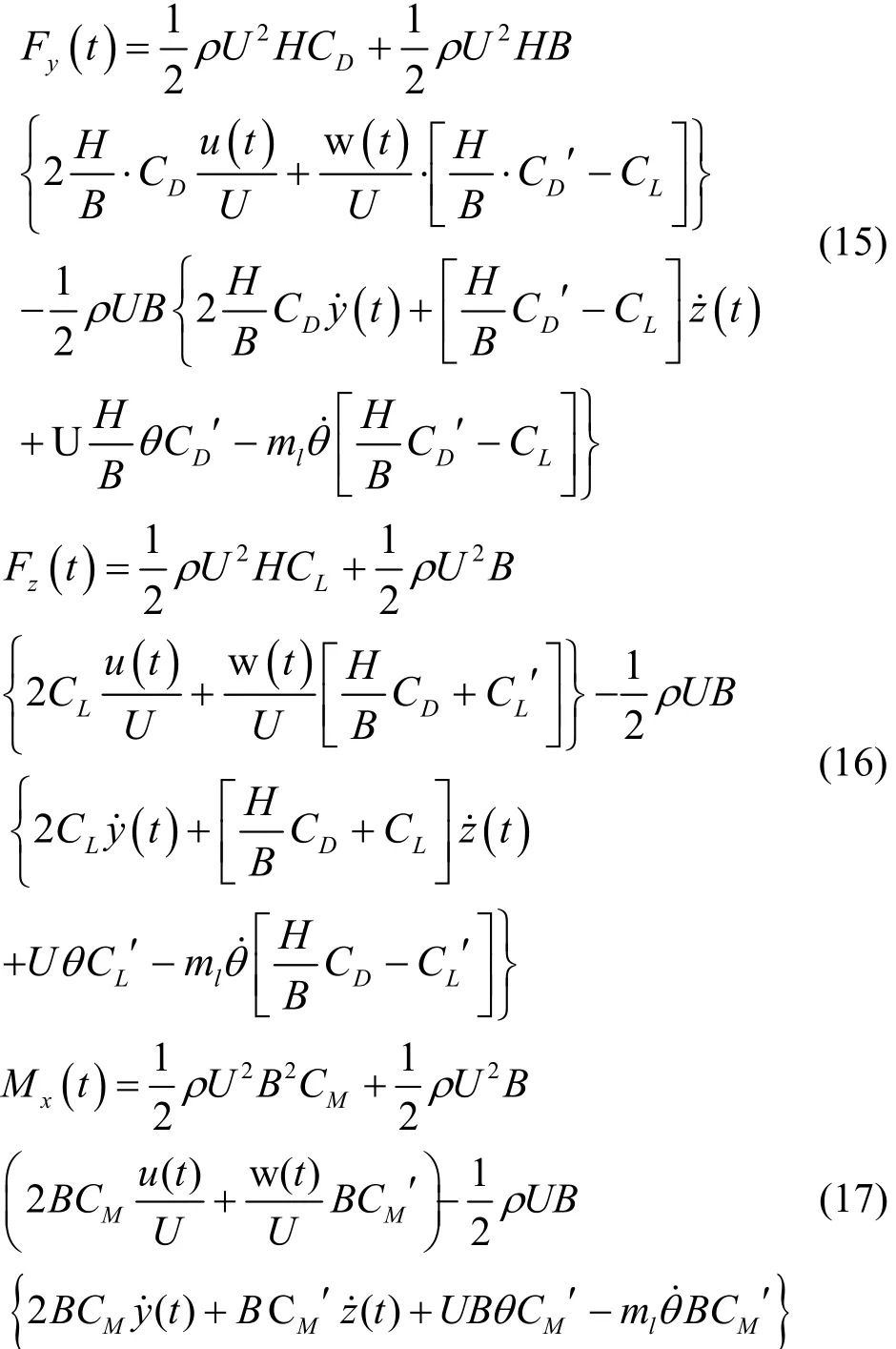
其中：()yt˙、()zt˙、θ˙分別為主梁截面處的速度和角速度；ml為主梁的特性長度．

從而，單位展長主梁截面上的自激力表示為

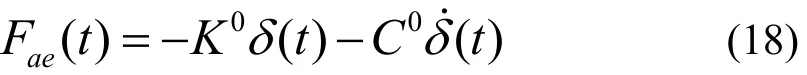
式中：K0、C0為單位展長氣動剛度、阻尼矩陣，其具體表達式見曾憲武等人的研究[11]；δ(t)、(t)δ˙為單元位移向量以及速度向量．

利用 ANSYS的自定義單元 Matrix27[4]，可以直接定義質量、剛度、阻尼矩陣，各矩陣的參數作為實常數來輸入，氣動自激力屬于非保守力，采用的是非對稱矩陣．氣動剛度矩陣和阻尼矩陣要分別建立單元，不能共用一個Matrix27單元．主梁跨中區域施加各參數值為端部四個單元（分別為兩個氣動剛度矩陣和氣動阻尼矩陣）的兩倍．

4 抖振響應分析

4.1 建模及風荷載

對結構進行有限元離散，有主纜、吊索、主塔、加勁主梁、橋墩等組成．主纜和吊索采用Link8單元模擬，主塔和橋墩采用Beam4單元模擬，加勁主梁采用Beam4單元模擬，主梁與主塔連接采用彈簧-阻尼單元Combin14和Mass21．利用ANSYS軟件建立了其三維有限元模型，全橋模型共有908個節點，869個單元，其中主纜單元164個，吊索單元102個，主塔和橋墩單元336個，主梁單元152個，其它的均為質量元．主梁采用空間魚刺模型，剛性魚骨刺橫梁和主塔通過主纜連接橫梁.此全橋空間有限元模型如圖2所示．在懸索橋結構的仿真模擬中, 主梁節點和吊索吊點采用剛性連接模擬，橋塔與主纜間采用剛性連接，主梁與橋塔采用彈性連接順橋向采用有阻尼約束方式模擬，全橋結構的邊界條件為兩個橋塔的底部完全固結，主纜在兩側錨定固結，在塔頂固結對于大跨度懸索橋而言，以恒載下的非線性靜力分析為基礎，動力響應是以恒載變形后的狀態下分析的，目的是驗證結構處于平衡狀態時的幾何位置是否合理．

圖2 全橋有限元模型Fig.2 Finite element model of PLT suspension bridge

對大跨度懸索橋進行動力特性分析得到其前十階振型如表1所示．由表可知，普立特懸索橋的基本周期為8 s左右，表現為主梁側向漂移和反對稱豎彎，頻率主要分布在0.12～1 Hz內，其分布較為密集，同時橋塔振動為主的振型出現較晚如橋塔反對稱側彎在31階發生，頻率約為0.84 Hz，故橋梁的動力特性主要表現為前幾階振型．

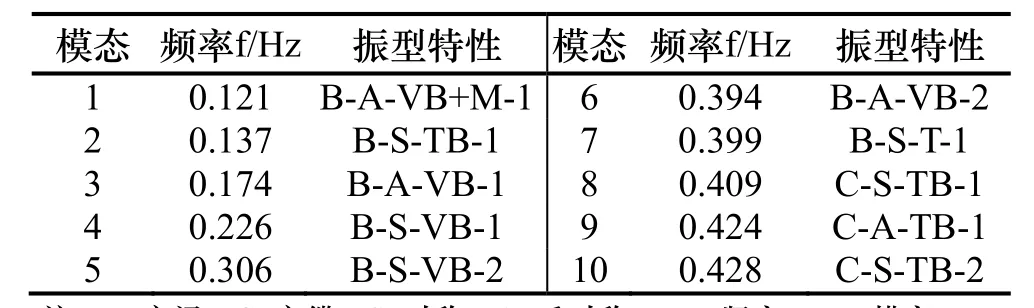
表1 橋梁的自振頻率及振型Table 1 Frequencies and modes of bridge

利用前述介紹的脈動風速的諧波合成法，采用Matlab編制相應脈動風模擬程序，對本橋主要的模擬參數如表 2所示．相干函數 Cohij(ω)如圖 3所示．從圖中可以看出，相關函數對其頻率的敏感度較強，當空間間距一定時，頻率越小，其相關函數越大.

表2 脈動風場模擬主要參數Table 2 Main parameters for fluctuating wind simulation

圖3 空間相干函數Cohij(ω)Fig.3 Spatial coherence function Cohij(ω)

模擬得到的主梁順風向及垂直向脈動風速時程結果如圖4所示．模擬得到的垂直向脈動風速功率譜與目標譜的對比如圖 5所示．通過對比可知，數值模擬得到的風場與目標吻合較好，驗證了模擬方法和所編寫模擬程序的可靠性及有效性．

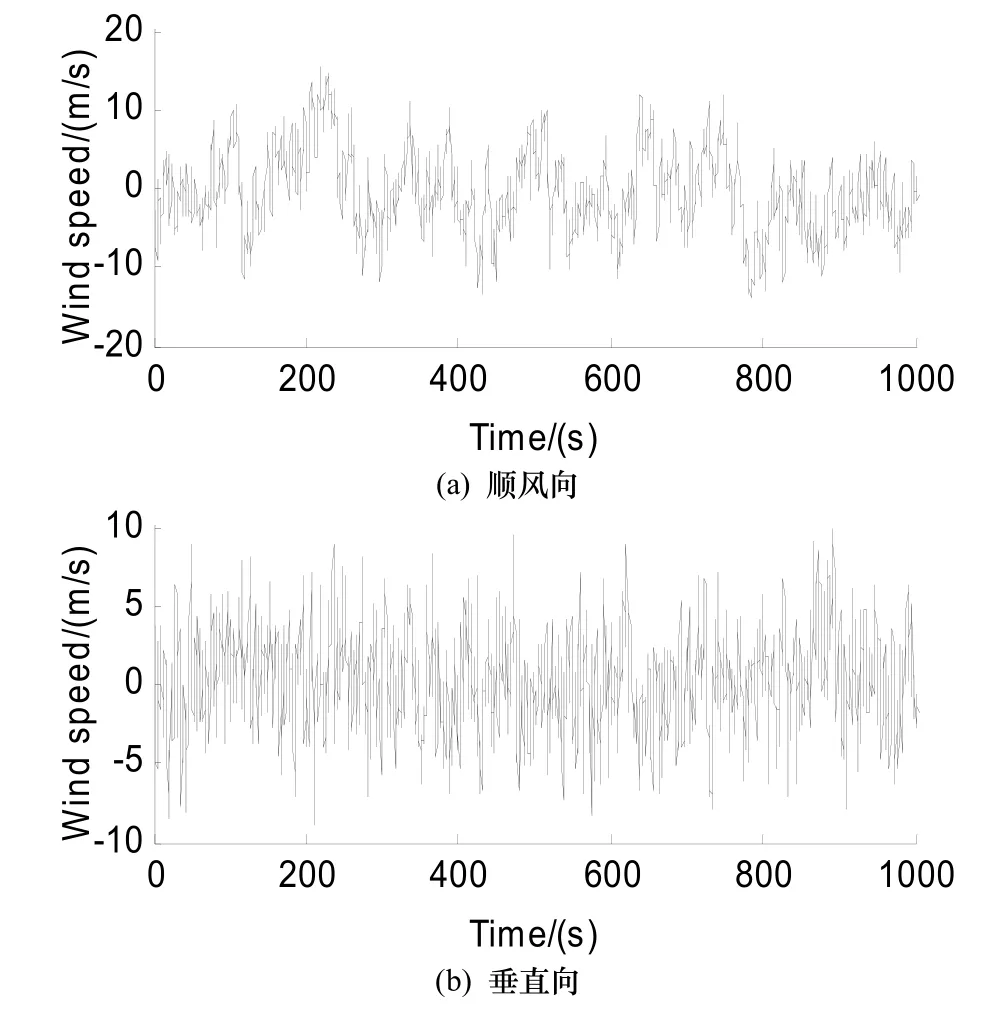
圖4 主梁跨中點模擬得到的順風向、垂直向脈動風速時程Fig.4 Time history of simulated longitudinal and vertical fluctuating wind speeds at middle point of the main span

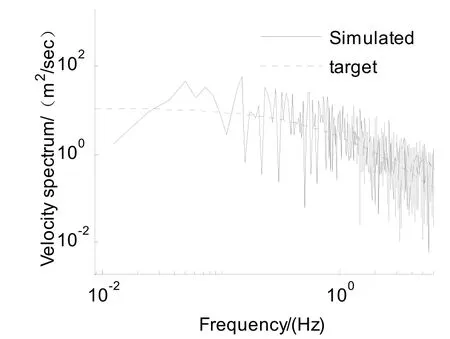
圖5主梁跨中點垂直向脈動風速功率譜對比Fig.5 Comparison of fluctuating wind spectrum at the middle point of main span

4.2 計算結果分析

脈動風速時程模擬完成后，采用基于準定常理論的抖振力計算公式，就可以將風速時程轉化為作用于橋梁的等效抖振力時程，此過程通過在Matlab軟件中生成數據文本并考慮節點的等效迎風面積，并利用ANSYS中的APDL進行二次開發即可實現，其中主梁在風軸坐標系下的氣動三分力系數如圖 6所示．結構的自激力分析采用 ANSYS自帶的MATRIX27單元輸入其氣動剛度矩陣和氣動阻尼矩陣的參數完成．計算中分別考慮了-12°～12°共25種工況，此處僅以0°工況為例進行結果分析．將得到的抖振力時程施加于該橋的有限元模型，編寫相應的循環加載批量數據和后處理程序，計算時間取1000s，分別計算了考慮與不考慮自激力作用時該橋的抖振響應，結果如圖7所示．計算中考慮結構的幾何非線性的因素，對此橋而言，幾何非線性主要來源于纜索的垂度效應、結構初應力和結構大變形三個因素的影響，采取措施是在ANSYS中打開幾何大變形開關（Nlgeon，on）、應力剛化（Stess stiffening）、更變坐標（upcood，1，on），并采用的Newmark-β方法計算橋梁的抖振響應．

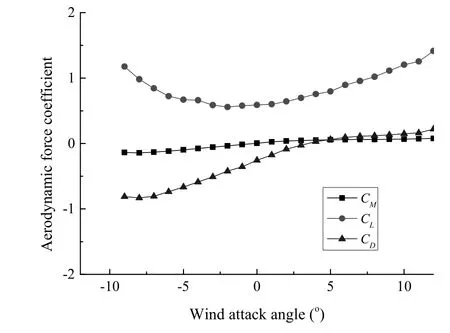
圖6 普立特懸索橋氣動三分力系數Fig.6 Aerodynamic coefficients of Pu Li Te bridge

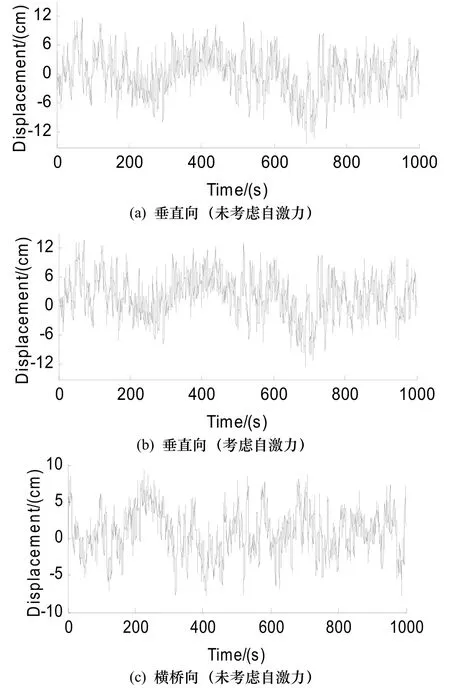
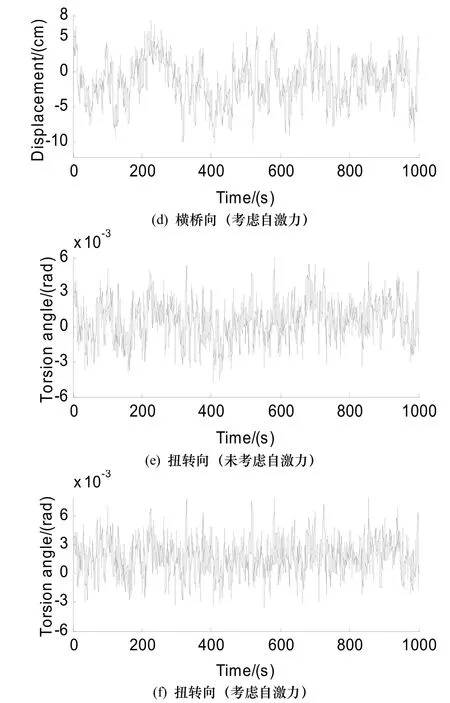
圖7 考慮和不考慮自激力作用下主梁跨中點的抖振響應Fig.7 Buffeting responses at the middle point of main span with and without considering self-excited forces

由圖可知，不考慮自激力作用時，主梁跨中節點處的垂直向、橫橋向及扭轉向抖振位移均以零為均值上下波動．通過對計算結果進行統計可知橫橋向位移響應的均方差為6.12 cm比垂直向位移響應的均方差5.08 cm大20%左右．考慮自激力作用時，垂直向位移響應均值有下降的趨勢，振動幅度也略有下降，此時自激力起到微弱的正阻尼作用．橫橋向及扭轉向位移響應均值均略有上升的趨勢，但整體振動幅度變化不是很明顯．總之，對本橋考慮了自激力作用后，較為明顯的作用是改變了橋梁振動的平衡位置，但自激力所起的正阻尼作用效果不明顯．

6 結論

本文根據普立特大跨度懸索橋的結構形式特點，結合脈動風相關特性，利用Deodatis的諧波合成法，很方便的對普立特大跨度懸索橋的脈動風場進行了模擬，并對模擬效果進行了檢驗，驗證了所采用模擬方法和所編模擬程序的可靠性及有效性．

通過利用ANSYS軟件完成了脈動風作用下普立特大跨度懸索橋橋梁考慮與不考慮自激力作用時的抖振響應計算．通過研究發現，考慮與不考慮自激力時計算得到的該橋抖振響應的振動幅度變化不大，主要作用在于改變了橋梁振動響應的平衡位置，自激力在局部方向(垂直向)的響應起到正阻尼的作用，另外，橫橋向橋梁抖振位移響應的均方差比垂直向大20%左右．整體來看，從橋梁抖振位移響應時程可以獲取比較全面的結構抖振力變形信息，為類似橋梁的抗風設計提供參考．

References

[1] 李小珍, 蔡 倩, 強士中. 蕪湖長江大橋主跨斜拉橋列車走行安全性與舒適性[J].交通運輸工程學報, 2002,2(3): 34-40.LI Xiaozhen, CAI Jing, QIANG Shizhong. Train running safety and comfort analysis of the cable-stayed bridge on Wuhu Yangtze-river Bridge [J]. Journal of Traffic and Transportation Engineering, 2002, 2(3): 34-40.

[2] DING Quanshun. Computer simulation of buffeting actions of suspension bridges under turbulent wind [J].Computers and Structures, 2000, 76(6): 787-797.

[3] 項海帆,陳艾榮. 特大跨度橋梁抗風研究的新進展[J].土木工程學報, 2003, 36(4): 1-8.XIANG Haifan, CHEN Airong. Recent advances in research on aerodynamics of extra long span bridges[J].China Civil Engineering Journal, 2003, 36(4): 1-8.

[4] ANSYS Inc. Theory reference and ANSYS APDL programmer’s guide [M]. http://www.ansys.com.cn

[5] ROSSI R, LAZZARI M, VITALIANI R. Wind field simulation for structural engineering purposes [J]. Numerical Methods in Engineering, 2004, 61(5): 738-763.

[6] DEODATIS G. Simulation of ergodic multivariate stochastic processes[J]. Engineering Mechanics, 1996,122(8): 778-787.

[7] HOLMES J D. Wind Loading of Structures[M]. 2nd ed.Taylor & Francis, Abingdon, 2007.

[8] SARKAR P P, JONES N P, SCANLAN R H. Identification of aeroelastic parameters of flexible bridge [J]. Engineering Mechanics, 1994, 120 (8):1718-1741.

[9] MIYATA T, YAMADA H, BOONYAPINYO V, et al.Analytical investigation on the response of a very long suspension bridge under gusty wind, Proc., 9th Int. Conf.on Wind Engineering, New Delhi, India, 1995, 1006-1017.

[10] 曾憲武, 韓大建. 大跨度橋梁風致抖振時域分析及在ANSYS中的實現[J]. 橋梁建設, 2004(1): 9-12.ZENG Xianwu, HAN Dajian. Time-domain analysis of wind-induced buffet on long-span bridges and implementation of analysis in ANSYS [J]. Bridge Construction, 2004(1): 9-12.