自由下落非均一粒徑顆粒流的流場特性

王 怡，樊 航，任曉芬,2

（1西安建筑科技大學環境與市政工程學院，陜西 西安 710055；2 河北工程大學城市建設學院，河北 邯鄲 056038）

在工業生產、散裝物料運輸等過程中，物料從高處下落到地面、料堆、料倉、或傳送帶時，會有大量顆粒物逃逸至周圍空氣中，這些游離的顆粒物不僅會對空氣造成污染，而且對人體健康和設備安全等產生一系列危害．

為了解決此類問題，前人運用實驗和數值模擬方法對自由下落物料進行了研究，研究內容主要集中在卷吸空氣量，顆粒流流場特性及產塵量等方面．Hemeon[1]假設顆粒流所受阻力為靜止空氣中單顆粒的受力之和，得出卷吸空氣量表達式．Tooker[2]對Hemeon的理論進行了一定程度的修改，他把顆粒流的整個下落過程視為充分發展的湍流運動，并且引入新的參數來計算卷吸空氣量．Cooper和Arnold[3]對卷吸空氣量做了進一步的研究而提出了顆粒羽流模型，并且通過實驗證明此模型對自由下落顆粒流卷吸量計算的準確性．Liu[4]通過實驗給出了一個經驗卷吸常數，提出新的兩相流模型來預測靜止空氣中自由下落顆粒的卷吸空氣量．Plinke[5-7]等探究了密度、下落高度、含濕量等因素對產塵量的影響，并得出一系列經驗公式．Koichiro Ogata[8]用激光測速儀測得均一粒徑顆粒流下落的軸心速度，得出軸心處顆粒沉降速度介于真空和受空氣阻力的單顆粒速度之間．Renaud Ansart[9]建立了兩相流模型計算出流口附近流場，利用PIV技術測試顆粒速度，所得結果預測Liu[4]模型中的速度分布．Uchiyama[10]采用渦方法描述了三種均一粒徑顆粒流的自由紊流射流場．王銳[11]等人利用三維格子渦方法模擬了均一粒徑顆粒流的速度場．

以上研究表明，已有研究大多以均一粒徑顆粒流為對象，關于非均一粒徑顆粒流的研究僅存在于對粉塵方面的研究中，對顆粒流流場特性的研究鮮有述及．在工業生產過程中，顆粒物都是以非均一粒徑形式存在的，均一粒徑顆粒流的流場特性對實際情況有一定的指導意義，但會造成較大的誤差．因此，對非均一粒徑顆粒流自由下落流場特性的研究非常必要．本文利用DPM-CFD的方法研究非均一粒徑自由下落顆粒流周圍的氣流速度分布、顆粒物的擴散及顆粒速度分布，以期對顆粒流自由下落時顆粒物的污染防治提供一定的參考依據．

1 數學模型

1.1 假設

1） 氣體相視為不可壓縮的連續相；

2） 顆粒視為球形，密度均勻；

3） 顆粒密度遠大于氣體密度；

4） 顆粒的體積分數小于10%，忽略顆粒物間的相互碰撞。

1.2 氣相模擬

對于假設的不可壓縮氣體相，忽略體積力，則氣相控制方程可以表示為：

連續性方程：

動量方程：

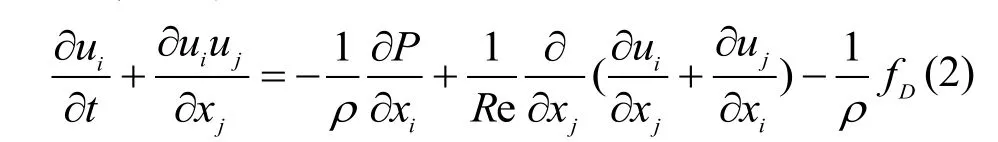
式中：i為x方向節點與界面的標號，j為y方向節點與界面的標號，ui、uj為氣相研究節點 i、j方向的速度分量，P為壓力，ρ為空氣密度，fD為單位控制體積的顆粒作用于氣體的阻力．

1.3 顆粒相模擬

顆粒流自由下落過程中，顆粒運動所受的作用力十分復雜，包括重力、氣體作用于顆粒的曳力、壓力梯度力、虛擬質量力、Magnus力、Saffman力、Basset力等，對于顆粒在湍流氣體中所受的軸向力，只考慮曳力即可[12]，其他力可以忽略不計，因此顆粒的作用力平衡方程式：

式中：m為單顆粒的質量，fD為單顆粒在空氣中所受阻力，g為重力加速度，uP為顆粒下降速度．

根據上述假設條件，阻力fD可表示為：

式中：u為空氣的速度，CD為顆粒的阻力系數，其表示為：

式中：ReP為顆粒雷諾數，表達式為：

2 物理模型及驗證

2.1 物理模型的建立

圖1為顆粒流下落計算區域示意圖，顆粒物通過寬度為D=0.006 m的條縫釋放到靜止空氣中，控制區為二維的0.8 m×1.5 m的長方形，被離散成9.18萬的網格，用來計算顆粒流自由下落的流場特性．

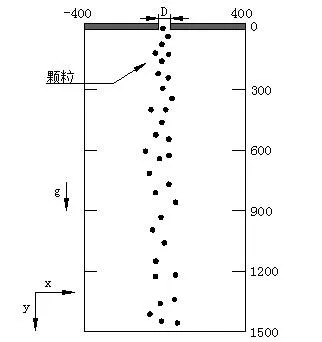
圖1 物理模型Fig.1 physical model

2.2 模擬條件

本文數值模擬顆粒入口的邊界條件設置為速度入口，空氣速度大小為0.001 m/s，左右兩側和底部界面設為自由出流邊界．在顆粒下落過程中，顆粒的體積分數小于 10%，故將氣相作為連續相考慮，采用標準 k-ε模型，顆粒相的模擬采用 DPM（Discrete Phase Model）模型．顆粒相湍流擴散采用隨機軌道模型，并考慮兩相之間的耦合．本文所用非均一粒徑分布符合Rosin分布，如表1所示，根據Rosin-Rammler方程進行分析計算得到此粒徑分布的平均值為300 μm．本文所用均一和非均一粒徑顆粒流的計算工況見表 2，顆粒流量設為 0.005 kg/s．

2.3 模型驗證

為了驗證本文所用數值模擬的可靠性，分別取dp=130 μm和dp=500 μm均一粒徑顆粒流進行模擬計算，所得結果分別與文獻[9]和[13]進行對比，并繪于圖2中.

由圖2（a）可以看出：數值模擬值和實驗值變值略小于實驗值，其原因是實驗所用顆粒物的粒徑存在一定誤差；而且實驗所用粉塵顆粒大都不是標準球形，所以會導致顆粒下落時所受曳力較之標準化規律基本一致，平均誤差值為10.07%．數值模擬球形顆粒具有一定偏差．總體而言，數值模擬結果和實驗結果一致較好．

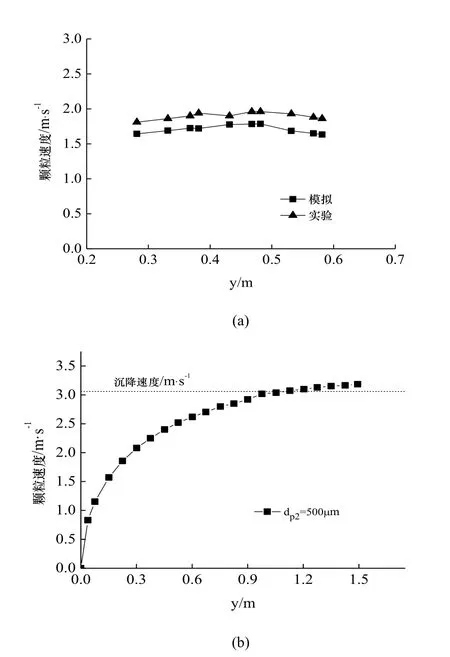
圖2 軸線顆粒速度分布Fig.2 The particle velocity distribution in axis line

圖2（b）所示，顆粒流下落高度Y＞900時，顆粒速度處于3～3.2 m/s之間，速度變化已經趨近于穩定值．本文引用文獻[13]的方法對 dp=500 μm的顆粒自由沉降速度計算如下：

表1 非均一粒徑顆粒流粒徑分布Tab.1 The size distribution of particles with non-uniform diameter

表2 數據模擬計算參數Tab. 2 calculation parameter of numerical simulation

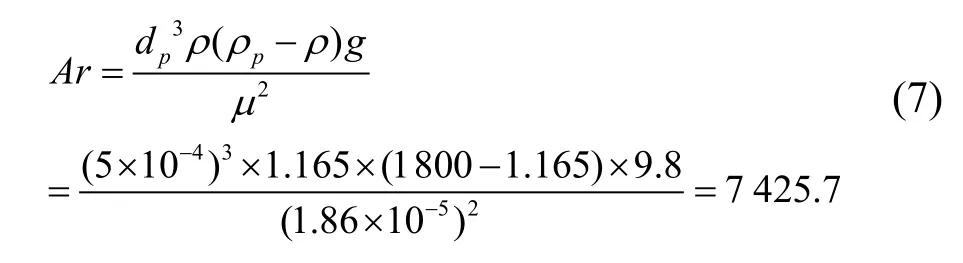
當Ar= 1 .83～3.5×105時，ReP和Ar呈下述關系式:

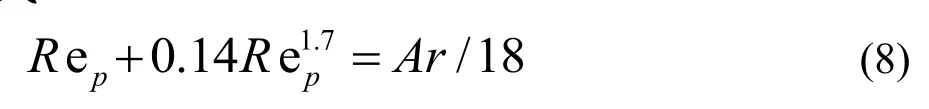
將（7）代入（8）得：ReP=94.5

計算顆粒自由沉降速度ut得：

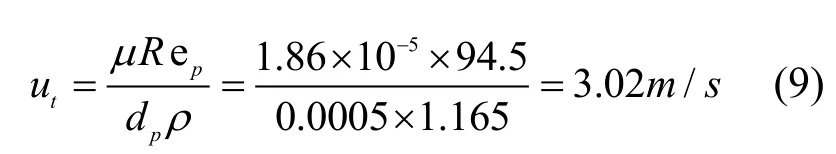
由此可見，模擬得到顆粒自由沉降速度ut與利用前人的計算方法[13]所得結果基本吻合．通過模型驗證表明了本文所用模型的準確性．

3 模擬結果與分析

3.1 非均一粒徑顆粒流氣流速度分布

同橫斷面的氣流分布，且圖中速度大小取絕對值．可以看出在不同高度下氣流速度變化規律基本相同：氣流速度沿徑向先減小后增加，隨后再次呈現下降趨勢，且在軸心處最大；軸心處的氣流速度隨著高度的增加而增加．在y1=0.2 m處，軸心附近氣流速度明顯小于下游同位置的氣流速度．隨著流動進一步發展，氣流速度增幅減小．在 y2=0.75 m處，|x|=0.08 m時氣流速度發生明顯突變，當下落高度達到y3=1.10 m時，氣流速度突變發生在|x|=0.12 m處．結合圖3可知，此下落距離內有漩渦形成，并且氣流速度方向改變．

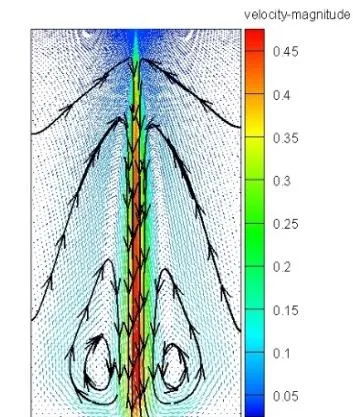
圖3 氣流速度矢量圖Fig.3 The vector graph of airflow velocity

圖4 不同斷面氣流分布Fig.4 The velocity distribution in different secti

圖5 y2=0.75m斷面氣流分布Fig.5 The velocity distribution in y2=0.75m section

圖 5所示為 y2=0.75m各工況斷面的氣流分布．由圖可知，氣流速度隨顆粒粒徑的減小而增大；隨著橫斷面半徑的增大，三種工況的氣流速度變化趨勢相同．這是由于相同流量下，隨著粒徑的增大，單位時間下落的顆粒數減少，顆粒與空氣的接觸面減小，從而使顆粒對氣流的影響減弱．非均一粒徑顆粒流的氣流速度介于dp1=150 μm和dp2=500 μm均一粒徑顆粒流之間．

3.2 非均一粒徑顆粒流擴散濃度

圖6顯示，在非均一粒徑顆粒流自由下落過程中，顆粒物濃度沿徑向逐漸減小，且擴散范圍隨著下落距離的增大而增加．y2=0.75 m和y3=1.10 m處軸心的顆粒物濃度遠遠小于y1=0.2 m處軸心的濃度，y1=0.2 m處擴散半徑僅為0.01 m，而達到y3=1.10 m時，擴散半徑顯著增大到0.07 m．該現象產生的原因是：隨著下落距離的增大，周圍空氣被不斷卷入顆粒流中，顆粒間隙率增大，因而造成擴散半徑逐漸增大．

圖6 不同斷面顆粒濃度Fig.6 The particle concentration in different section

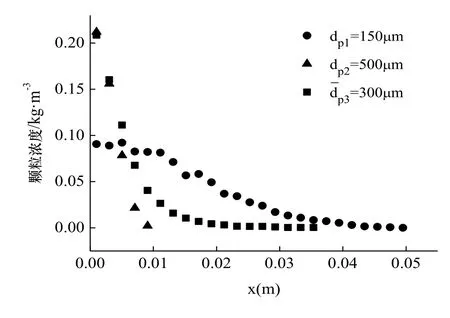
圖7 y2=0.75m斷面顆粒濃度Fig.7 The particle concentration in y2=0.75m section

圖7所示y2=0.75m各工況下顆粒流濃度沿徑向的變化規律，由圖可知，擴散半徑受顆粒流粒徑的影響非常顯著，粒徑越小，擴散半徑越大．根據數據分析，此斷面上dp1=150 μm的均一粒徑顆粒流擴散半徑為=300 μm 的非均一粒徑顆粒流的 1.5倍．當x≥0.005 m時，與dp1=150 μm的均一粒徑顆粒流相比較，非均一粒徑顆粒流的顆粒物濃度反而較小．

3.3 非均一粒徑顆粒流顆粒速度分布

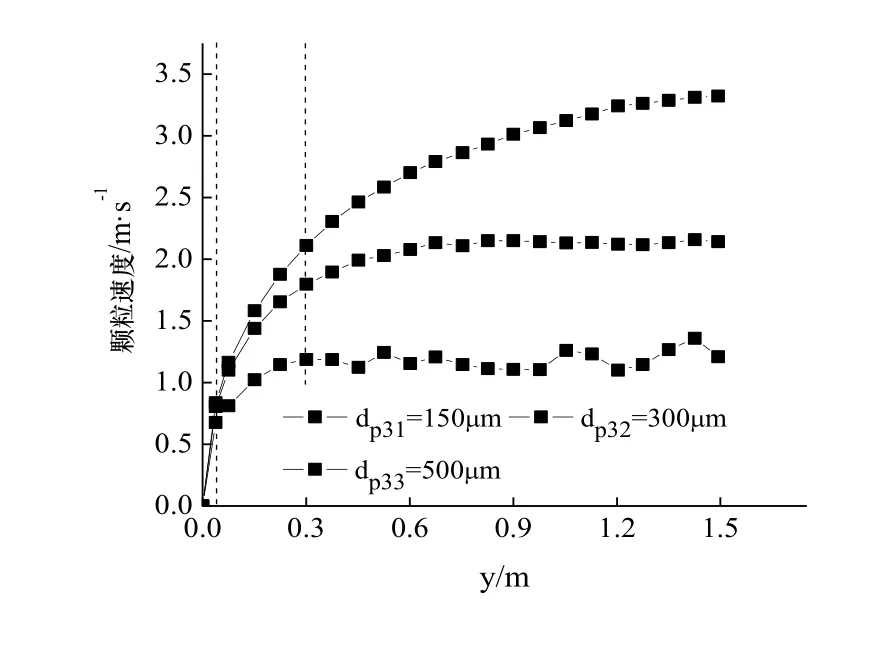
圖8μm非均一粒徑的顆粒速度分布Fig.8 Particle velocity distribution of non-uniformsize when=300μm

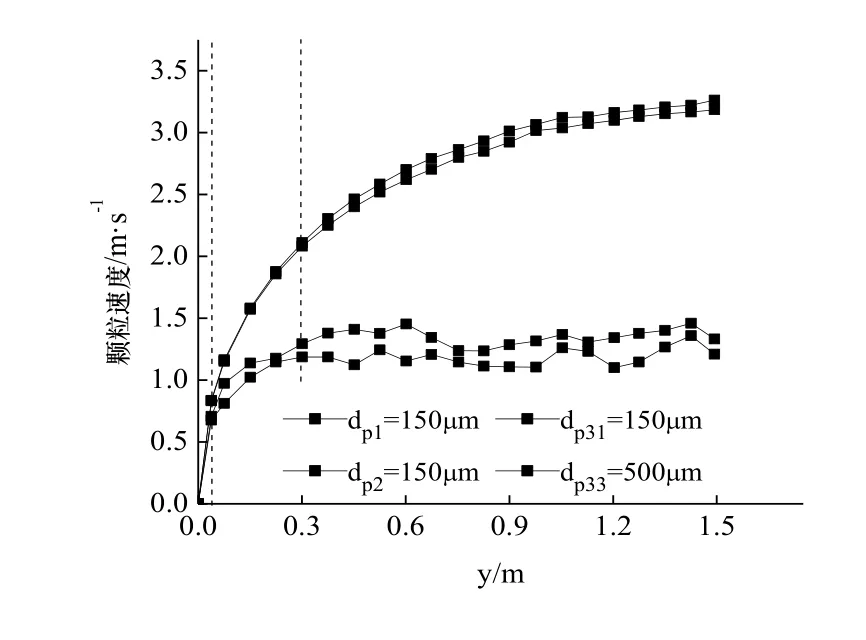
圖9 不同工況同粒徑的顆粒速度分布Fig.9 Particle velocity distribution of uniform size in different cases

圖9將非均一粒徑工況和均一粒徑工況進行比較，可以看出均一粒徑與非均一粒徑顆粒流中 500 μm 的顆粒速度分布基本一致，而非均一粒徑工況的150 μm顆粒速度比均一粒徑工況小，且后者約為前者的1.13倍．原因是處于非均一顆粒流邊緣的小粒徑顆粒濃度相比150 μm均一粒徑顆粒流濃度較小，顆粒體積分數減小，作用在每個顆粒上的空氣摩擦力增加，導致顆粒速度減小．

根據上述分析，由擴散半徑和顆粒沉降速度的變化情況可知，非均一粒徑顆粒流中大顆粒對小顆粒的擴散半徑和沉降速度均有影響，且對擴散半徑影響更大．

4 結論

為了考察自由下落非均一粒徑顆粒流的流場特性，本文采用數值模擬方法對顆粒與空氣耦合作用下的氣流速度分布、顆粒擴散規律以及顆粒速度分布進行了研究，得出以下結論：

(1)顆粒流下落會導致空氣沿垂直方向形成向下的射流；在本文研究范圍內，射流兩側出現漩渦，且漩渦覆蓋y2=0.75 m和y3=1.10 m兩處；氣流速度隨著顆粒粒徑的增大而減小．

(2)顆粒物濃度沿徑向逐漸減小，且擴散范圍隨著下落距離的增大而增加；在同一高度，粒徑越小，顆粒流擴散半徑越大，y2=0.75 m時dp1=150 μm的顆粒流擴散半徑為d—p3=300 μm擴散半徑的1.5倍．

(3)顆粒流自由下落時，顆粒速度的增幅由快到慢，逐漸趨于平緩；與均一粒徑相比，非均一粒徑下的同粒徑小顆粒具有更小的沉降速度，因此小粒徑顆粒流中混入大顆粒可使其沉降速度減小．

References

[1] HEMEON W C L. Plant and process ventilation[M]//Plant and process ventilation. Industrial Press, 1963: 120-161.

[2] TOOKER G E. Controlling fugitive dust emissions in material handling operations[J]. Bulk Solids Handling,1992, 12(2): 227-32.

[3] COOPER P, ARNOLD P. Air entrainment and dust generation from a falling stream of bulk material[J].KONA Powder and Particle Journal, 1995, 13(0):125-134.

[4] LIU Z Q. Air entrainment in free falling bulk materials[D]. University of Wollongong, 2001.

[5] PLINKE M A E, LEITH D, HOLSTEIN D B, et al.Experimental examination of factors that affect dust generation[J]. The American Industrial Hygiene Association Journal, 1991, 52(12): 521-528.

[6] PLINKE M A E, MAUS R, LEITH D. Experimental examination of factors that affect dust generation by using Heubach and MRI testers[J]. The American Industrial Hygiene Association Journal, 1992, 53(5):325-330.

[7] PLINKE M A E, LEITH D, BOUNDY M G, et al. Dust generation from handling powders in industry[J].American Industrial Hygiene Association, 1995, 56(3):251-257.

[8] OGATA K, FUNATSU K, TOMITA Y. Experimental investigation of a free falling powder jet and the air entrainment[J]. Powder technology, 2001, 115(1): 90-95.

[9] ANSART R, RYCK de A, DODDS J A, et al. Dust emission by powder handling: comparison between numerical analysis and experimental results[J]. Powder Technology, 2009, 190(1): 274-281.

[10] UCHIYAMA T. Numerical analysis of particulate jet generated by free falling particles[J]. Powder technology,2004, 145(2): 123-130.

[11] 王銳, 陳斌. 三維格子渦方法模擬自由下落顆粒群[J].工程熱物理學報, 2014, 35(3): 499-502.WANG Rui, CHEN Bin. Numerical simulation of free falling particles by three-dimensional vortex-in-cell method[J]. Journal of Engineering Thermophysics, 2014,35(3): 499-502.

[12] 施學貴,徐旭常,馮俊凱. 顆粒在湍流氣流中運動的受力分析[J]. 工程熱物理學報,1989, 10(3): 320-325.SHI Xuegui, XU Xuchang, FENG Junkai. The analysis of forces on particles moving in turbulent flow[J]. Journal of Engineering Thermophysics, 1989, 10(3): 320-325.

[13] 王寶和, 王喜忠. 計算球形顆粒自由沉降速度的一種新方法[J]. 粉體技術, 1996, 2(2): 30-39.WANG Baohe, WANG Xizhong. New method for calculation of settling velocity of a spherodial particle[J].Powder Science and Technology, 1996, 2(2): 30-39.