中央空調中一類不確定性模型的MFAC研究

馮增喜，任慶昌

（西安建筑科技大學信息與控制工程學院，陜西 西安 710055）

一階慣性加滯后是控制系統中常見的數學模型，例如中央空調中的壓差控制模型、溫差控制模型、送風溫度控制模型、風機靜壓控制模型等．若一階慣性加滯后的數學模型準確，則根據其滯后時間可有多種對應的控制方法．若滯后時間小，可采用PID及PID的變種算法來控制．若滯后時間較長，則可采用大林算法、Smith預估控制算法等．然而，實際中許多系統的數學模型存在很大的不確定性或模型難以建立，則致使部分控制算法失效．例如，Smith預估控制太過依賴精確的數學模型，當估計模型和實際對象有誤差時，控制品質會顯著惡化，甚至發散，而且對于外部擾動也非常敏感，魯棒性較差[1]．

針對中央空調由于運行過程中設備老化、非線性和外部因素等原因造成一階慣性加滯后模型的不確定性的情況，使用無模型自適應控制（Model Free Adaptive Control，MFAC）方法來研究其對模型參數不確定變化的適應性．侯忠生教授曾提到“當受控系統的數學模型完全未知時，或者是受控系統的模型的不確定性很大時，或者是受控過程結構變化很大時，很難用一個數學模型來表述時，或建模成本與控制效益不好時，應該考慮應用無模型控制方法[2]．” 盡管MFAC文獻[2]及其它相關文獻得出了以上概括性結論，然而受控系統的數學模型多樣，不同的模型具有不同參數和結構，而不同參數和結構由于不確定性的變化對 MFAC性能的具體影響尚缺少研究，即MFAC對模型結構和各參數不確定性變化的適應性強弱缺乏研究，這對控制算法的選取有很大的影響，且并非所有受控系統模型的不確定性很大時均可采用MFAC．如本研究發現對于一階慣性加滯后系統，當系統的滯后時間變化較大時，選取 MFAC方法，則控制結果變化不太大．而當系統的過程增益和時間常數變化較大時，則MFAC方法不可取．為了探索MFAC方法對模型參數變化的適應性，并更好地運用MFAC方法，針對具有不確定性的一階慣性加滯后系統，通過仿真技術研究系統的滯后時間、過程增益和系統時間常數單參數變化以及這3個參數中雙參數變化和三參數變化時，MFAC方法控制性能的具體變化．這對MFAC的應用范圍進一步細化，同時也為針對具有不確定性的一階慣性加滯后系統的控制方法的選取也提供了依據．

1 無模型自適應控制

MFAC使用了一種新的動態線性化方法及偽偏導數（或偽梯度；或偽雅可比矩陣）的新概念，在閉環系統的每個動態工作點處建立一個虛擬等價的動態線性化數據模型，然后基于此虛擬等價的數據模型設計控制器，并進行控制系統的理論分析，進而實現非線性系統的參數和結構自適應控制[2]．MFAC具有以下優點： MFAC僅依賴于被控系統實時量測的數據，不依賴受控系統任何的數學模型信息；MFAC方法不需要任何外在的測試信號、試驗或訓練過程； MFAC方法簡單、計算負擔小、易于實現、魯棒性強[3-6]．本文采用基于緊格式動態線性化的MFAC方案進行研究．

1.1 無模型自適應控制算法

針對一般離散時間系統有：

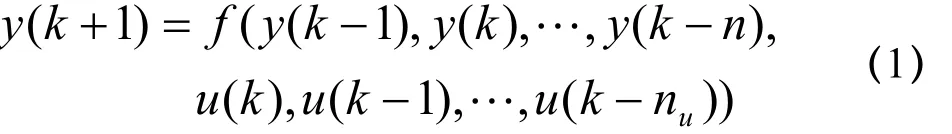
式中： y ( k)、 u ( k)分別表示系統的輸出和輸入，u( k)是p維輸入， ny、 nu表示系統輸出、輸入階數， f (···)是輸出關于輸入的函數．

無模型控制的“泛模型”如式（2）所示：

針對如公式（1）所示受控系統及其泛模型， 采用基于緊格式動態線性化數據模型的 MFAC方案．無模型控制方法的控制律基本形式如式（3）所示[3]：

1.2 無模型自適應控制算法流程

基于緊格式動態線性化數據模型的無模型自適應控制算法的流程如圖1所示．

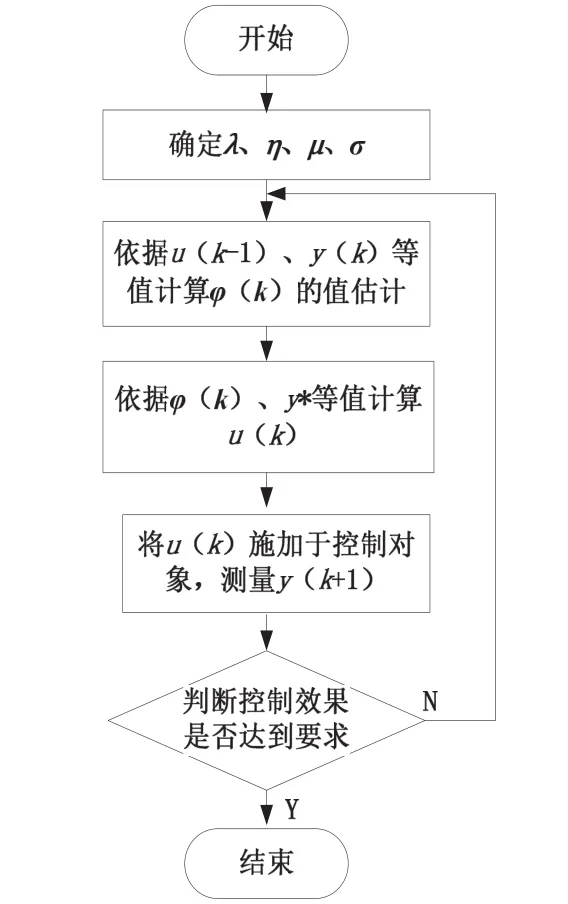
圖 1 MFAC算法流程圖Fig.1 The flow chart of MFAC algorithm

2 仿真研究

2.1 仿真對象及參數設置

中央空調風機控制數學模型如式（5）所示．

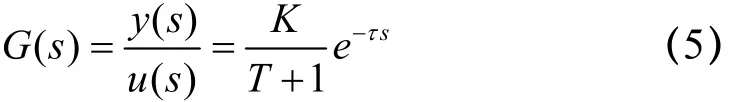
式中：u為風機輸入頻率，單位為Hz；y為風管靜壓，單位為Pa；K為過程增益；T為時間常數，單位為s; τ為滯后時間，單位為s．

由于風機的非線性，以及運行過程中設備老化、非線性和外部因素的原因，式（5）的參數會發生變化，具有不確定性．在某一時期通過辨識建立的風機靜壓模型如式（6）所示[7]．參考文獻[7]的成果，最終確定K、T和τ三個參數的變化范圍分別為[3，6]、[4，8]和[2，10]．

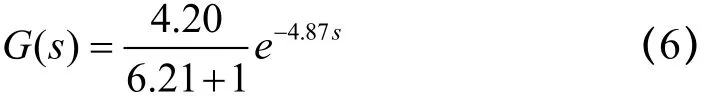
為了在不同參數不同變化的情況下，對比傳統PID和MFAC的控制效果．將K、T和τ的變化情況分為三類：單參數變化、雙參數變化和三參數變化，具體的模型參數變化如表1前3列所示．PID和MFAC的參數取值如下：kP=0.184 2，kI=0.023，kD=0.221 8； μ=1.55，λ=1.65，η=0.009，ρ=0.14．

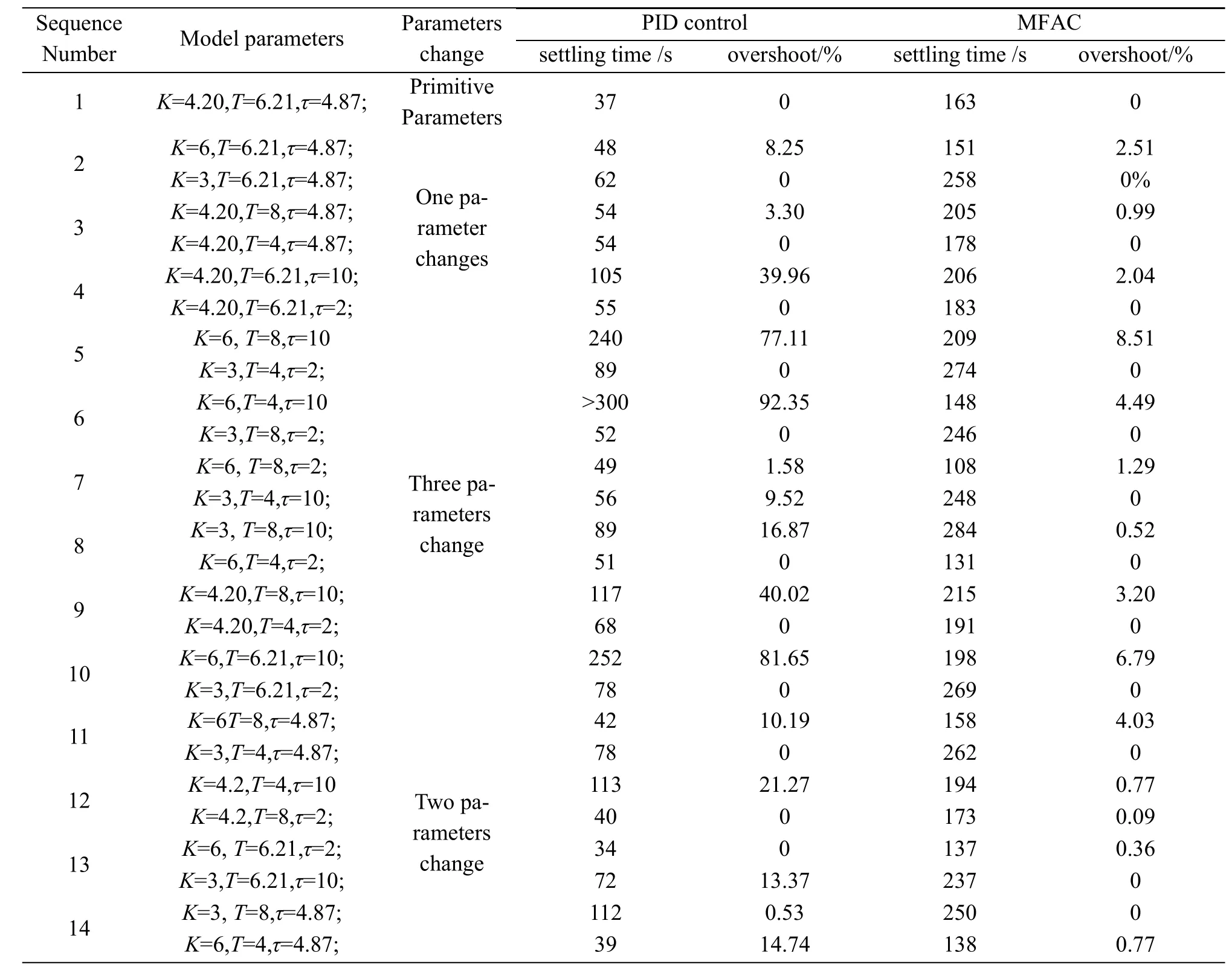
表1 模型參數變化及仿真結果對照表Tab.1 The model parameters and simulation results

針對三類參數變化的 14種情形，分別進行了PID和MFAC控制仿真．不同仿真結果統計如表1的后4列所示．由于篇幅所限，在此僅給出了6組參數的仿真結果．針對模型原始參數的仿真如圖2．

圖2 原始參數仿真Fig.2 The simulation based on primitive parameters

針對過程增益K、時間常數T和滯后時間τ 三個單參數變化仿真分別如圖3、圖4和圖5．圖6和圖7分別是三參數變化和二參數變化的仿真．

圖3 參數K變化的仿真Fig.3 The simulation based on changed parameter K

圖4 參數T變化的仿真Fig.4 The simulation based on changed parameter T

圖5 參數τ變化的仿真Fig.5 The simulation based on changed parameter τ

圖7 二參數變化仿真Fig.7 The simulation based on two changed parameters

2.2 仿真結果分析

對于原始模型的控制，本研究仿真結果表明，兩種方法的超調量均為0%．采用PID控制的調節時間為 37 s，采用 MFAC控制的調節時間為 163 s．就抗擾性能而言，在 t=200 s時加入幅值為 10的擾動，采用PID控制的輸出出現波動，其大小為-2.26，對此擾動的調節時間為17 s；采用MFAC控制的輸出出現較小波動，其大小為0.39，對此擾動的調節時間為15 s．這表明采用MFAC時，系統抗擾性能很好，穩定性好，且受到干擾時恢復時間短．

關于模型參數變化對控制性能的影響，從單參數、三參數和二參數變化3種情況對其進行分析．

（1）模型單參數變化對控制性能影響

① 過程增益K變化對控制性能的影響．由圖3可知，對于PID控制，K增大為6時，調節時間變長為48 s，超調量為8.25 %；K減小為3時，調節時間變長為62 s，超調量為0 %．對于MFAC控制，K增大為6時，調節時間變長為151 s，超調量為0 %；K減小為3時，調節時間變長為62 s，超調量為0 %．由此可得：過程增益K的變化，對于PID控制，使原來整定的最佳PID參數變為非最佳，從而導致調節時間變長，而K的增大導致系統的超調量變大，K的減小維持系統的超調量不變．而對于MFAC控制，K的變化導致控制效果類似于PID控制，但是超調量的變化小于PID．

② 時間常數T變化對控制性能的影響．由圖4可知， T的變化，對于PID控制，對其調節時間影響不大，主要影響了超調量，T增大導致了超調量增大，在本研究中T減小不影響超調量．對于MFAC控制，T的增大或減小均使調節時間變長，T的增大導致了超調量增大，但其超調量的變化小于PID控制中T增大引起的超調變化量，T減小不影響超調量．

③ 滯后時間τ變化對控制性能的影響．由圖5可知，對于PID控制，滯后時間τ的增大和減小均使調節時間變長，τ的增大導致系統超調量變大，τ的減小維持系統的超調量不變．對于MFAC控制，τ的增大和減小均使調節時間變長，τ的增大導致系統超調量略微變大，τ減小維持系統的超調量不變．

（2）模型三參數變化對控制性能的影響

① 三個參數全部變大時，兩種方法的調節時間均變長，超調量均變大．相對而言，PID控制方法中的超調量變化遠大于 MFAC控制方法中的超調量變化．三個參數全部變小時，兩種方法的調節時間均變長，超調量均減小．

② 三個參數變化方向不一致時，由于仿真結果受到各個參數變化幅值大小的影響及其共同作用，特別是對PID控制，故難以得出其變化規律，而對于MFAC，可得出變化的總體趨勢：總體變化趨勢是調節時間變長，超調量變化較小．

（3）模型二參數變化對控制性能的影響

對于模型中兩個參數發生變化的情況同三個參數變化方向不一致的情況基本一致．對于PID控制，難以得出其變化規律，對于MFAC，總體變化趨勢是調節時間變長，超調量變化較小．

綜合以上分析，可得出如下結論：①MFAC的抗擾性能優于PID．若系統受到干擾，采用MFAC方法，系統具有很好的抗擾性、穩定性、較短的恢復時間．②從對調節時間和超調量的影響來講，若單參數變化，對于MFAC而言，過程增益K的變化對調節時間影響很大，慣性時間常數T和滯后時間τ的變化對調節時間影響較小，而這三個參數的變化對超調量的影響都很小．對于PID控制而言，過程增益K和滯后時間τ的變化對超調量和調節時間的影響都比較大，而慣性時間常數T對超調量影響較大，對調節時間影響較小．若多參數同時變化，對于MFAC，總體變化趨勢是調節時間變長，超調量變化較小．對于PID控制，由于3個參數均在變化，最終的控制效果受到3個參數變化幅值的影響，致使控制效果有可能較好，也有可能較差．但是若控制性能變差，主要體現在超調量變化過大，而超調量變化引起調節過程較長．超調量變化過大的原因在于滯后時間常數的變大，這也說明對于一階慣性加滯后環節的非線性系統，滯后時間越長，非線性程度越嚴重，更適合MFAC控制．因此，對于抗擾性、穩態性要求高、延時較大時且延時具有不確定性的系統，可采用MFAC控制．

關于針對具有不確定的一階慣性加滯后的模型，進行MFAC和PID性能研究時，還需注意以下兩點：①參數變化范圍不能過大，若參數變化過大，兩種方法最終都將變得無效．②若進行實驗比對時，由于對象模型的不確定性，每種方法均要至少實驗兩次，兩次實驗間隔較長的一段時間．但兩種方法的同參數實驗應在同一時段進行，否則可能會出現與仿真結果不一致的情況．

3 結論

針對中央空調系統中一階慣性加滯后模型的不確定性，根據過程增益、時間常數和滯后時間3個參數的不同變化，進行了14種情形的仿真，分析不同參數變化對無模型自適應控制性能的影響，并與PID的控制性能進行了對比，結果表明對于抗擾性要求高、延時較大時且延時具有不確定性的系統，可采用MFAC控制．

References

[1] 金尚泰. 無模型學習自適應控制的若干問題研究及其應用[D]. 北京：北京交通大學, 2009.JIN Shangtai. On model free learning adaptive control and applications[D]. Beijing : Beijing Jiaotong University,2009.

[2] 侯忠生. 無模型自適應控制的現狀與展望[J]. 控制理論與應用, 2006,23(4):586-592.HOU Zhongsheng. On model free adaptive control: the state of the art and Perspective Control[J]. Theory & Applications, 2006,23(4):586-592.

[3] 侯忠生,許建新. 數據驅動控制理論及方法的回顧和展望[J].自動化學報, 2009,35(6):650-667.HOU Zhongsheng, XU Jianxin. On data-driven control theory: the state of the art and perspective[J]. Acta Automatica Sinica, 2009,35(6):650-667.

[4] 韓志剛. 關于建模與自適應控制的一體化途徑[J].自動化學報,2004,30(3):380-389.HAN Zhigang. An integrated approach to modeling and adaptive control[J]. Acta Automatica Sinica, 2004,30(3):380-389.

[5] 韓志剛. 一類復雜系統非建模控制方法的研究[J].控制與決策,2003,18(4):398-402.HAN Zhigang. Study on non-modeling control method for a class of complex systems[J]. Control and Decision,2003,18(4):398-402.

[6] 韓志剛. 無模型控制器的設計問題[J].控制工程,2002,9(3):19-22.HAN Zhigang. Designing problem of model free controller[J]. Control Engineering of China, 2002,9(3):19-22.

[7] 楊世忠,任慶昌. 基于風機模型不確定性的魯棒控制[J].測控技術,2013,32(10):69-74.YANG Shizhong, REN Qingchang. Robust control based on fan model uncertainty[J]. Measurement & Control Technology, 2013,32(10):69-74.