基于廣義似然比的冗余慣組故障檢測方法研究
武唯強,閆 杰,溫 琦
(西北工業大學 航天學院,陜西 西安 710072)
使用備份慣性器件構成冗余捷聯慣組(Redundant IMU,RIMU)的方式可以明顯提高導航、制導系統的可靠性。對于捷聯慣組基于廣義似然比法的故障檢測技術國內外學者均進行了深入研究。國內學者賈鵬[1]介紹了廣義似然比法(GLT)、均值檢驗法,以及局部估計方法等常用的故障診斷方法,驗證了這幾種方法在檢測小故障時實際應用的不同效果,并分析了影響各自檢測能力及故障時延的原因及在工程應用中的優缺點。李延龍[2]針對冗余配置的慣導系統漸變型故障,提出了奇偶方程殘差品質的概念及其模糊評估方法;并應用殘差品質構成最小二乘加權陣,設計了冗余配置的慣導系統智能自適應漸變型故障容錯方法。魏偉[3]針對余度傳感器捷聯慣導系統軟故障檢測的漏警率和虛警率高,以及多個軟故障難以檢測的問題,對Potter等人的廣義似然比方法(GLT)加以改進,增加了檢測兩個和兩個以上軟故障的能力。張玲霞[4]對SINS中冗余配置的傳感器量測系統的軟故障,研究了目前常用的廣義似然比檢驗(GLT)和最優奇偶向量校驗(OPT)方法;對基于系統量測方程和狀態方程的動態系統,研究了系統的魯棒故障檢測與診斷(FDD)方法。國外學者P.Motyka[5]等人詳細介紹了故障的分類、閾值的選取方法,并對邊緣向量檢測法和廣義似然比法這兩種故障檢測方法進行了介紹。Daly[6]等詳細研究了基于冗余慣組配置的故障檢測與隔離方法——廣義似然比,并介紹了其在不同慣組配置下的應用方案。HONG JIN[7]等介紹了基于奇偶空間結構的奇偶向量定義方法,并描述了其在傳感器誤差檢測與隔離中的應用。Steven Ray Hall[8]介紹了故障檢測與隔離算法中的奇偶向量的定義,并提出采用濾波的方式來補償由于刻度系數誤差、漂移和安裝誤差引起的奇偶向量誤差,從而對慣組誤差進行了建模和估計。某工程單位需要對3種冗余配置的捷聯慣組進行故障檢測效果的比對分析。論文研究的目的是研究廣義似然比法在3種配置下的應用。
1 問題描述
1.1 冗余慣組配置
配置方案一:三套慣組(兩套激光慣組+一套光纖慣組)共支架、共基準同方位捷聯安裝。每個方向均有3個陀螺儀測量輸出三路角增量信息,3個加速度計測量輸出三路速度增量信息,安裝如圖 1所示。
配置方案二:兩套捷聯慣組三正交一斜置冗余,共基準安裝。每一套慣組由4個陀螺儀和4個加速度計組成,一個陀螺儀和一個加速度計組成一組測量組件,共四組。其中三組正交安裝,一組以任意方向斜置安裝。每一套捷聯慣組安裝如圖2所示。
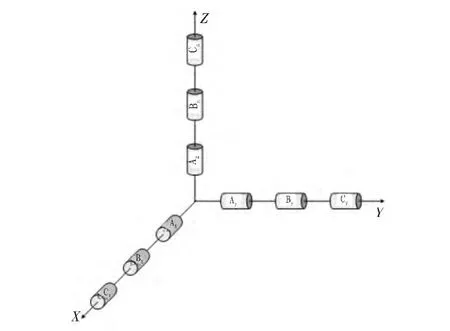
圖1 三套慣組同軸冗余配置Fig.1 Three sets of IMU coaxial redundancy configuration

圖2 三正交一斜置配置Fig.2 Three orthogonal and an oblique configuration
配置方案三:捷聯慣組三正交兩斜置冗余共支架、共基準安裝。由5個陀螺儀和5個加速度計組成,一個陀螺儀和一個加速度計組成一組測量組件,共5組。其中三組正交安裝,兩組以任意方向斜置安裝,如圖 3所示。
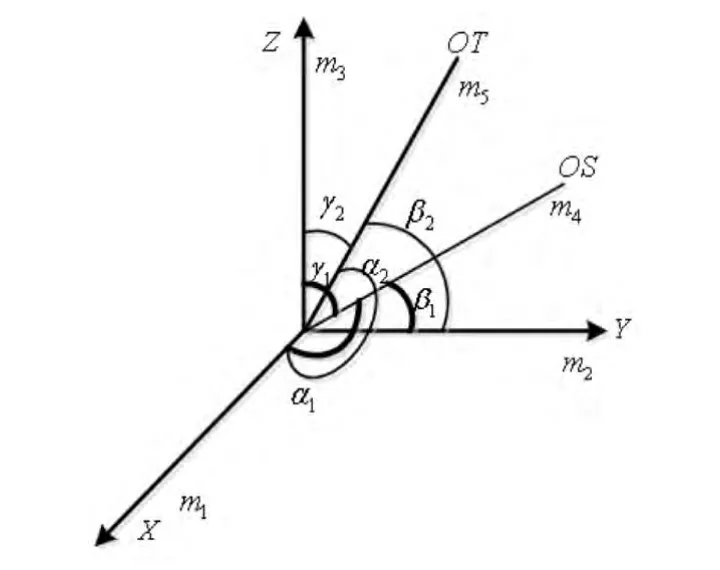
圖3 三正交兩斜置冗余配置Fig.3 Three orthogonal and two oblique redundant configuration
1.2 廣義似然比法
等價空間(或方程)法的基本思路是根據系統的硬件冗余或解析冗余方程,構造一個等價矩陣,用實際觀測量來檢查系統數學模型(解析冗余關系)的等價性(一致性),尋找與系統故障解耦的等價方程,構造奇偶向量(等價向量)和故障檢測函數,這樣便可進行故障檢測與診斷。就奇偶空間而言,直接冗余(傳感器的個數多于系統狀態的個數)較簡單,用到的系統數學模型僅有量測方程;間接冗余(傳感器的個數不多于系統狀態的個數)還需用系統狀態方程。當測量矩陣有誤差(如儀表安裝誤差,刻度因子誤差等)和儀表有測量偏差時,奇偶向量將與狀態和測量偏差有關,使故障檢測與診斷不準。
根據產生解耦矩陣的方式不同,等價空間法又可分為:廣義似然比法,最優奇偶向量法,奇異值分解法等。
無故障測量方程:Z=HX+ε
Z:m維測量向量;
H:安裝矩陣;
X:n維真實狀態;
ε:測量噪聲,假設為高斯白噪聲,均值為0,協方差陣為R=σ2I。
選取系統解耦矩陣V,滿足:
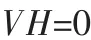
解耦矩陣V可由Potter算法得到。
那么,定義奇偶殘差向量p=VZ,可得:
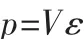
發生偏差故障時,測量方程為:
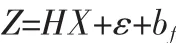
其中,bf為故障向量。
此時的奇偶殘差p為:
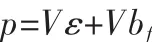
奇偶殘差p在無故障假設H0和有故障假設H1情況下的統計特性為:
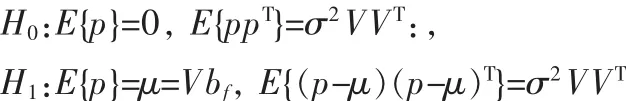
正是因為在有無故障時,殘差的統計特性不同,才為故障的診斷提供了基礎。
兩種假設的對數似然比為:
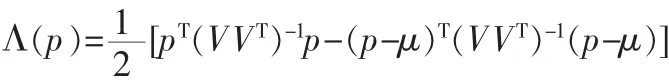
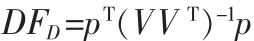
故障判決準則為:
若 DFD>TD,則判斷有故障;
若DFD≤TD,則判斷有故障。
當檢測判決函數超出預設閾值后,才進行故障隔離。
檢驗m個假設:
Hi:第 i個傳感器發生偏差故障,i=1,2,…,m。
假定第j個傳感器發生故障,即bf=ejf,那么μ=Vbf=Vejf=fvj,式中Vj是矩陣V的第j列。
此時奇偶殘差p的統計特性為:

似然估計為:
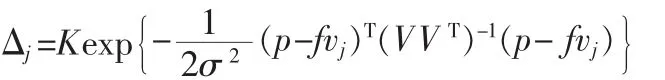
K是常量。
f的最大使然估計為:
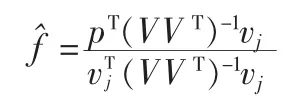
帶入似然方程并取對數得隔離判決函數:
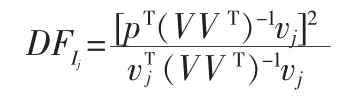
分別計算 DFIj,( j=1,2,…m),值最大的就是最可能故障的。
廣義似然比法故障檢測流程如圖4。
2 仿真分析
配置一,三套三正交捷聯慣組
安裝矩陣Hn為:

根據Potter算法,可由幾何安裝矩陣Hn算得相應的解耦 矩陣V:
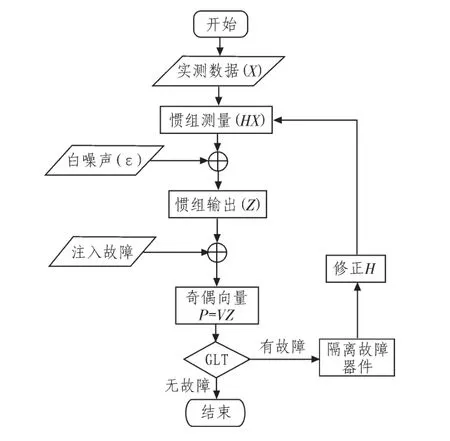
圖4 廣義似然比法故障檢測與隔離仿真試驗流程圖Fig.4 Generalized likelihood ratio for fault detection and isolation simulation flow chart

在進行故障檢測時,由于野值點的存在,必須進行處理,否則誤警率會很高。

圖5 無故障時的故障檢測函數野值點Fig.5 Outliers of fault detection function without fault
對野值點的處理采用兩點判決法或三點判決法。兩點判決法,連續兩個判決函數值超出閾值,即認為發生故障。三點判決法,連續三個判決函數值超出閾值,即認為發生故障。
采用兩點(三點)判決法是一種折中的處理方法。它會帶來故障檢測的延遲,卻不會增大閾值。利用蒙特卡洛仿真試驗法得到無故障時兩點(三點)判決法的誤警率。

表1 GLT法配置一的誤警率Tab.1 The false alarm rate of configure 1 using GLT method
可以看出,采用三點判決法的誤警率非常低,而且只是帶來了3個采樣周期的故障延遲。因此,在進行故障的漏警試驗時,采用三點判決法。
配置二,兩套三正交一斜置冗余配置
安裝矩陣Hn為:

根據Potter算法,可由幾何安裝矩陣Hn算得相應的解耦矩陣V:


表2 GLT法配置二的誤警率Tab.2 The false alarm rate of configure 2 using GLT method
配置三,三正交兩斜置(十表)冗余配置
安裝矩陣Hn為:

根據Potter算法,可由幾何安裝矩陣Hn算得相應的解耦矩陣V:
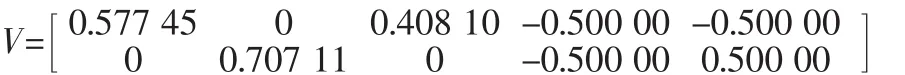

表3 GLT法配置三的誤警率Tab.3 The false alarm rate of configure 3 using GLT method
3 結 論
冗余捷聯慣組可以提高導航、制導系統的可靠性,廣義似然比法是常用的故障檢測算法,論文針對某工程中3種冗余配置的捷聯慣組,研究廣義似然比法對3種配置故障檢測中的應用,對誤警率進行比較分析得出采用十表冗余配置的捷聯慣組誤警率最小。
[1]賈鵬,張洪鉞.基于奇異值分解的冗余慣導系統故障診斷[J].宇航學報,2006,27(5):1076-1080.JIA Peng,ZHANG Hong-yue.Fault detection for redundant inertial navigation system based on SVD method[J].Journal of Astronautics,2006,27(5):1076-1080.
[2]李延龍,吳訓忠.一種冗余配置的慣性導航系統漸變型故障容錯方法[J].彈箭與制導學報,2008,28(2):57-60.LI Yan-long,WU Xun-zhong.Gradual fault-tolerance design of redundant SINS[J].Journal of Projectiles, Rockets,Missiles and Guidance,2008,28(2):57-60.
[3]魏偉,陸志東,秦永元.余度傳感器捷聯慣導軟故障檢測[J].中國慣性技術學報,2009,17(1):111-116.WEI Wei,LU Zhi-dong,QIN Yong-yuan.Soft fault detection of redundant sensor SINS[J].Journal of Chinese Inertial Technology,2009,17(1):111-116.
[4]張玲霞.導航系統故障檢測與診斷及其相關理論問題的研究[D].西安:西北工業大學,2004.
[5]Motyka P,Landey M,Rn R M.Failure detection and isolation analysis of a redundant strapdown inertial measurement unit[R].Cambridge:The Charles Stark Draper Laboratory,Inc.,1981.
[6]Daly K C,Gai E,Harrison J V.Generalized likelihood test for FBI in redundant sensor configurations[J].Guidance and Control,1979,2(1):9-17.
[7]JIN H,ZHANG H Y.Optimal parity vector sensitive to designated sensor fault[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(4):1122-1128.
[8]Hall SR.Parity Vector Compensation for FDI[D].Aeronautics and Astronautics,1981.

