推進器輔助系泊系統的動態張力控制
秦煜婷,陳紅衛,袁文亞
(1.江蘇科技大學 電子信息學院,江蘇 鎮江 212003;2.淮安遠航船用設備制造有限公司 江蘇 淮安 223001)
我國正處在高速發展時期,原油進口與日俱增,而后備石油資源嚴重不足,陸上石油資源有限,可以預見,我國海洋石油開發的下一個高潮即將在深海領域中進行。位置系泊系統的商業應用源于上世紀八十年末期,是應用于永久海上石油平臺的不錯的備用方案。上世紀七十年代開始,位置系泊系統的研究主要是基于動力定位系統研究的經驗。文獻[1]提出了基于最優控制和卡爾曼濾波的動力定位系統;文獻[2]是對文獻[1]理論的發展。近年來,提出了積分反向遞推技術[3]。在文獻[4]中,通過解懸鏈線方程提出了一種基于錨泊線特性的錨泊系統模型,且最優控制器被引用到此系統中。最近幾年,更先進的控制器,基于觀測器反向遞推和最優反向遞推方法發展起來。
在較深或環境惡劣的水域,定位中需加入推進器輔助系統。為了更好的達到資源有效利用,我們要盡可能的較少燃料損耗。由此,們使用動態張力錨泊線來消除連續或者慢變的干擾,如:平均風力、平均流力和潮汐流力,連同縱蕩、橫蕩、艏搖上的阻尼,航向的控制。
1 數學模型
數學模型的研究包含船舶剛體子模型和錨鏈的偏微分方程模型。用有限元方法進行錨鏈方程的空間離散化。綜合考慮邊界條件,建立船舶錨泊動力學模型。
1.1 坐標系
在環境因素(風浪流)復雜的海況下,無約束的船體表現為6個自由度的運動,實際的船舶定位系統中,只考慮3個自由度的運動:縱蕩、橫蕩與艏搖。為了研究船舶的運動,需要建立兩個坐標系,如圖1,XOY為相對于地球的固定坐標系,xoy為相對于船體的隨船坐標系,兩者的Z軸垂直指向地心。
用向量η=[X,Y,ψ]表示船舶在固定坐標系下的位置和艏向角度,用V=[u,v,r]表示船舶在隨船坐標系下的速度,兩者之間存在轉換關系:

其中,轉換矩陣為:


圖1 地坐標與船體坐標系Fig.1 Earth-fixed and body-fixed reference frames
J(ψ)為非奇異矩陣,且滿足 J-1(ψ)=JT(ψ)。
1.2 船舶運動學
三自由度的船舶低頻運動模型可以描述為
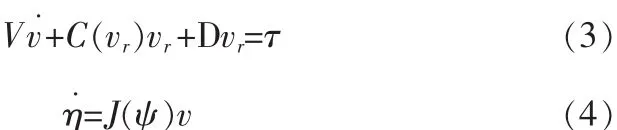
其中

vc(Z)∈R3為大地坐標系中海流的速度,M為慣性矩陣,C為向心矩陣,D為阻尼矩陣,τ由環境力(除了流力,因為在定義vr的時候已經考慮進去)和推進力組成。在船舶狀態保持的應用中,舶速很小,C(vr)vr可被忽略,且D被認為是常數。
1.3 多纜錨泊系統
忽略彎曲和扭轉剛度的纜運動方程為:
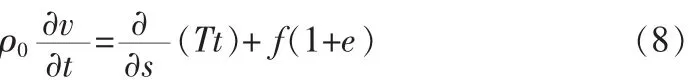
式中:s∈[0,L]為沿未拉伸錨線的距離,L為未拉伸錨線的長度。v(s,t)∈R3為錨鏈速度,t(s,t)∈R3為切向矢量。ρ0為錨線單位長度的質量,T 為張力,e 為拉伸形變率,f(s,t)為微元所受合外力。引入位置向量r(s)∈R3,應用胡克定律得:

式中:E為楊氏系數 (彈性模量),A0為纜的橫截面積,有關系e=。合外力的表達式為:

其中:fhg為單位錨線上的浮力,fdt為單位切向水動力阻力,fnd為單位法向水動力阻力,fnm為單位水動力慣性力。水動力由莫里森方程建模,表達式如下:

式中:g∈R3為重力加速度,ρc和ρw分別為纜繩密度和所處環境中水的密度,CDT為纜繩切向阻力系數,CDN為法向阻力系數,d為纜的直徑,CMN為水動力質量系數,vt和vnt分別為纜繩切向速度和法向速度,an為加速度的法向分量。
利用有限元模型研究多纜錨泊系統[5]。模型中,多纜錨泊系統中的每條纜繩都被分成n段,節點編號為-n,在大地坐標系中,第j條纜的第k個節點表示為,相對速度表示為=-vc(),vc()為處水流的速度,邊界條件為:1)每個纜的第一個節點固定在纜底。2)所有纜繩的終點在水面上匯聚成一點,==…=。
為了研究方便,定義如下工程量:
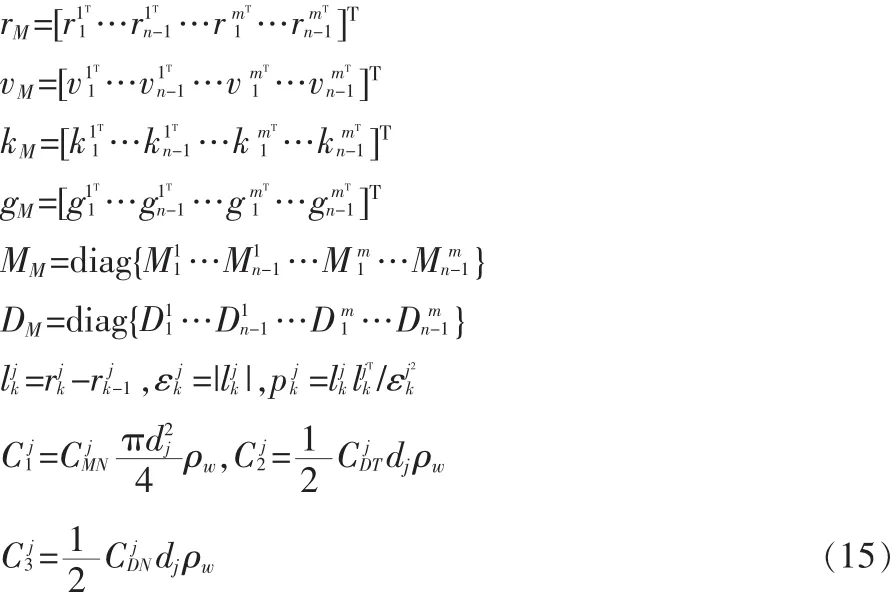

錨泊運動學方程為:
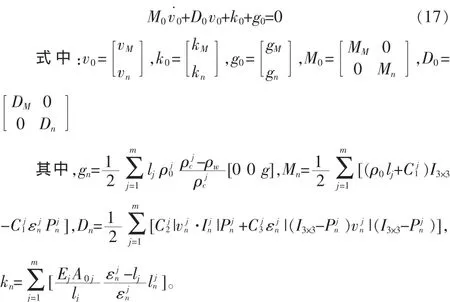
1.4 船舶錨泊動力學模型
在3個自由度下對船舶動力學進行研究,包括其位移和水平面上的旋轉。因此,當所有錨泊線的上端點連接到船舶轉臺上時,錨泊系統需考慮以下邊界條件:
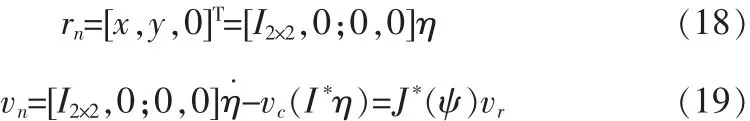
與Mn和Dn有關的部分可以被忽略,推出下面錨泊船的完整運動方程。
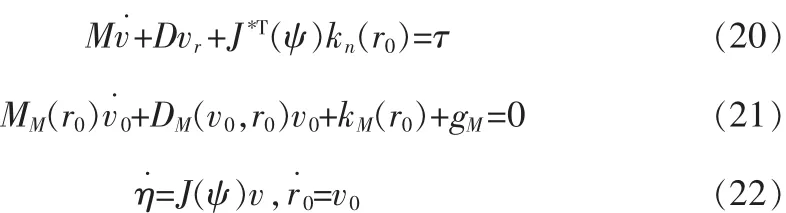
2 參考自適應控制器的設計
源于物理的無源性的概念,它將輸入輸出的乘積作為能量的供給率,體現了系統在有界條件下能量的衰減特性。事實上,基于李雅普諾夫函數的穩定性理論,也可從無源性的角度加以解釋,無源性與穩定性有著不可分的關系。因果動態系統中,無源性與穩定性是等價的。纜繩動態張力控制器的設計基于如下兩條假設:1)船舶已配置動力定位系統。2)船舶可以實時的測量錨線上的張力。
以τc表示動力定位控制器計算出的執行力,τm為錨泊力投射到水平面上的力,定義推進器的力為[6]:

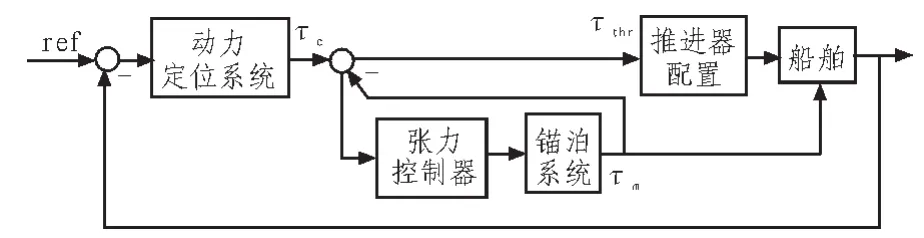
圖2 動力輔助錨泊定位船系統框圖Fig.2 Block diagram of thruster assisted mooring positioning system
因此,推進器輔助錨泊系統的性能完全取決于動力定位控制器。動態張力控制器的目的是追蹤,使得執行力盡可能少的分配給推進器,通常來說,控制問題是:
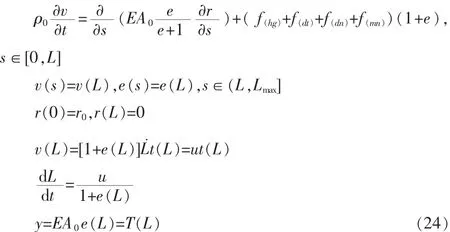
找到 u(t)確定 y(t)的參考值 Tref,以上公式中,r(L)=0,即DP系統被假設成理想的分析模型。船舶距期望位置的偏差被視為噪聲。Tref在一定的區間內由靜態錨線特性給出。存在L*∈[Lmin,Lmax],r*(s)和 e*(s)滿足:

并且 Tref=EA0e*(L*)。
將附加質量加到等式左邊:

包含水動力附加慣量的慣量矩陣是常數,即M˙c=0。可證明系統(24)是嚴格無源的,既滿足:

動力定位錨泊船的慣性矩陣相比于閉環系統的動態特性將要緩慢變化。因此M˙=0,是一個好的假設。通常,慣性矩陣取決于浪的頻率,船和錨鏈的速度。然而,在工業控制系統應用中,這些都可以忽略。
3 仿真實驗
仿真對象選擇錨線長度為2 250 m的深海錨泊船,錨泊線選擇密度為5 500 kg/m3的合金材料。目前,在流體作用力的研究中,很大一部分工作是集中在如何得到可到的水動力系數上。在這方面,無論在實驗或者實地測試上都積累了相當的數據,但是,實驗情況會存在尺度效應所引起的誤差,實地測試也存在著技術和精度方面待解決的問題。在一些規范中,則直接給出了CM,CD的取值范圍和要求。如挪威船級社(DNV)規定在 Stokes五階波時,CDN取 0.5~1.2,CM取 2.0;API規定在應用 Stokes流理論時,CDN取 0.6~1.0,CM取 0.5~1.2。 質量矩陣 M=[9.6×107,0,0;0,1.3×108,-5.3×109;0,-5.3×109,5×1011],阻尼矩陣 D=[9.2×105,0,0;0,2.4×106,-9.7×107;0,-9.7×107,1.3×1010],仿真時錨泊線的 速度為 Vc(z,t)=-cos(t/6 875);sin(t/6 875);0]z[0,1 000]。
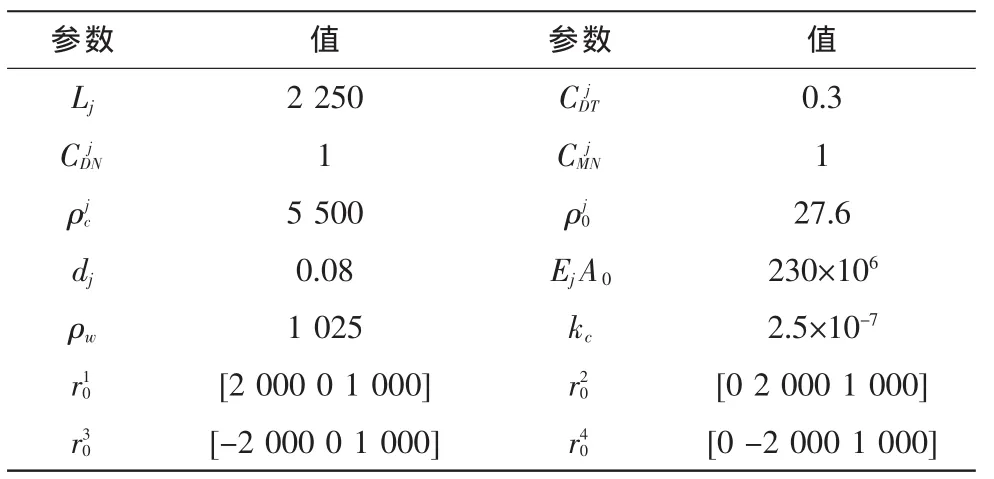
表1 仿真所用參數Tab.1 Parameters used in the simulation
仿真可簡單的表明動態錨鏈張力控制減少燃料消耗的作用。仿真只考慮潮汐流的干擾。表1為用到的仿真參數。動力定位系統的描述參見文獻[7],張力控制器追蹤執行力τc。錨泊系統為四根錨鏈,錨點均勻分布在以2 km為半徑的圓上。彼此相對的錨線相對于原點以相同的速度纏繞,執行力以這樣的方式分配到纜繩上。此控制策略用P控制器實現。

kc為控制器增益,τc表示執行力,τm為錨泊力,B 是 m×3的通過錨點給出的配置矩陣:


圖3 上下兩圖非別為x方向執行力(虛線)和推進器的力(實線),y方向執行力(虛線)和推進器的力(實線)Fig.3 Commanded (dotted) and thruster forces(solid) in the xdirection(upper graph) and y-direction(lower graph)
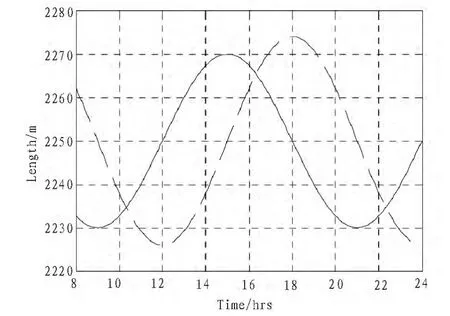
圖4 正x方向(虛線)和正y方向(實線)的錨線長度Fig.4 Length of cables at positive x-axis (dotted) and positive y-axis(solid)
圖3 顯示了動力定位系統計算出的執行力和推進器分配的力。如預期,推進器的力很小,意味著張力控制器很好的跟蹤了執行力。圖4為正x和正y方向的錨泊線的長度。通過兩幅仿真圖可以看出,在平穩環境條件下,錨泊系統提供大部分的執行力,推進器提供很小的一部分環境力。
4 結 論
文章中首先研究了船舶運動,并用有限元法對錨泊進行運動分析,構建成錨泊船的整體運動方程。隨后,設計動力輔助錨泊控制系統并證明了系統的無源性。計算機仿真表明:令錨泊系統補償持續慢變的環境力,推進器補償快變的干擾,可以減少船舶燃料的使用。
[1]Balchen J G,Jenssen N A,Saelid S.Dynamic Positioning Using Kalman Filtering and Optimal Control Theory[J].IFAC/IFIP symposium on Automation in Offshore Oil Field operation,1976:183-188.
[2]Balchen J G,Jenssen N A,Mathisen E,et al.A dynamic positioning system based on kalman filtering and optimal control[J].Modeling, Identification and Control,1980,1(3):135-163.
[3]Fossen T I,Grφvlen A.Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping[J].IEEE Transactions on Control Systems Technology,1998,6(1):121-128
[4]Strand JP,Sφrensen A J,Fossen T I.Modelling and control of thruster assisted position mooring systems for ships[J].IFAC,1997:160-165.
[5]余龍,譚家華.錨泊線與海底接觸的有限元建模及其非線性分析[J].中國海洋平臺,2005(2):25-29.YU Long,TAN Jia-hua.Finite element modeling mooring line contact with the seabed and nonlinear analysis[J].China Offshore Platform,2005(2):25-29.
[6]Fossen T I,Strand JP.Passive nonlinear observer design for ships using lyapunov methods:Full-scale experiments with a sypply vessel[J].Automatica,1999,35(1):3-16.
[7]Fossen TI,Strand JP.Nonlinear ship control[M].Fukaoka,Japan:IFAC,1998.

