室內環境溫控系統建模研究

吳 豪 ，方潛生 ，楊亞龍

（1.安徽建筑大學 電子與信息工程學院，合肥 230022；2.安徽省智能建筑重點實驗室，合肥 230022）

熱舒適是人對周圍熱環境所做的主觀滿意度評價[1]。影響人體熱舒適的因素主要有環境因素（空氣溫度、平均輻射溫度、相對濕度、氣流速度）和個人因素（人體活動量、衣著情況），其中空氣溫度是最為主要的可控因素[2]。

隨著我國經濟發展以及人民生活水平的提高，人們對室內環境舒適性要求日益增高與能源愈發緊張的矛盾越來越嚴重，這就迫使尋找最佳熱舒適方案。空調是改善室內環境熱舒適狀況不可或缺的一部分，近年來出現的地板送風、工位送風等新的空調形式，在一定程度上緩解了上述矛盾。然而空調控制系統比較復雜，運行過程中受各種不確定因素（人員流動、門窗啟閉、生產工藝、設備散熱等）影響，精確的數學模型很難確定，經典控制方法難以兼顧節能與舒適的要求。因此建立室內環境溫度的精確數學模型并研究室內環境的溫控特性具有非常重要的意義。

目前，許多學者對此做了相應的研究，文獻[3]用一階慣性環節加純滯后環節表示室內環境溫度的模型，但是每個特性參數所代表的意義及如何確定均沒有明確給出；文獻[4]用國內常用的估算公式確定特性參數，然而實際建筑結構多呈現不規則性和不對稱性，由估算公式建立的模型精度不高；文獻[5]沒有考慮干擾因素的影響。本文在已有研究的基礎上，結合機理分析和系統辨識2種建模方法，確定室內環境溫度的數學模型，并對建立的模型進行分析研究。在原有控制系統的基礎上加入模糊控制的思想，考察改進控制系統的控制效果。

1 室內環境溫度數學模型的建立

通常系統數學建模的方法有2種：機理分析法和系統辨識法。本文將這2種方法結合起來，建立室內環境溫度的數學模型。

首先，通過機理分析，了解空調房間溫度變化機理，根據空調房間的熱平衡方程，獲得所需數學模型的基本形式，利用估算公式得到房間的估算模型；接著進行階躍響應辨識，對獲得的空調出風口溫度和室內溫度進行處理，采用最小二乘法擬合曲線，獲取模型的各個參數，對建立的模型進行研究，考察本文方法所建模型的合理性。

1.1 室內環境的機理分析

本文選取安徽省智能建筑重點實驗室的人體熱舒適度研究室為研究對象，室內配有一臺下送風方式的恒溫恒濕空調。該空調房間作為被控對象，具有多容、大熱容量、大時延等特性，由此建立的動態數學模型應是高階微分方程。然而為了便于實際研究而又不失真實性，通常需要合理的簡化，例如：把整個房間視為一個單容的系統，忽略房間內部氣體流動，假定房間內部溫度分布均勻，忽略太陽輻射的影響等。

根據上述假設并結合實際，該空調房間的示意圖如圖1所示。

圖1 空調房間示意圖Fig.1 Schematic of the air conditioning room

整個空調房間遵循能量守恒定律，即：單位時間內房間的蓄熱量=（單位時間內進入室內空氣的熱量+單位時間內室外向室內傳入的熱量+單位時間內設備、照明和人體產生的散熱量）—（單位時間室內向室外排出空氣的熱量）

列出上述關系的數學表達式，并參考文獻[6]，用帶有滯后的一階慣性環節來描述該空調房間的溫度對象，其傳遞函數為

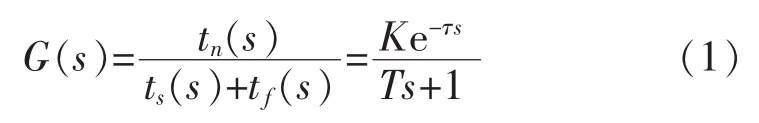
其中：tf為室內外干擾量換算成送風溫度的變化量，℃；放大系數K為房間溫度每降低1℃所需加入的冷量；時間常數T反應房間受到干擾后，室內溫度達到新的穩定值的快慢程度；房間受到干擾后，調節參數不能立即發生變化，需要過一段時間才開始變化，這段時間成為滯后時間τ。在ts和tf共同作用下，空調房間模型結構圖如圖2所示。

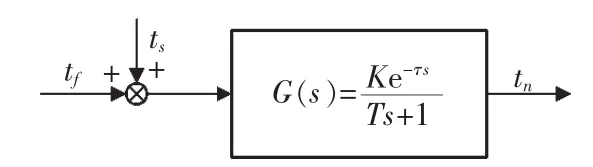
圖2 空調房間模型結構圖Fig.2 Structure chart of the air conditioning room model

測量實驗所用房間獲得如下參數：

1）房間圍護結構尺寸

房間長L=8.4 m，寬W=6.1 m，凈高H=2.5 m，窗戶1個，窗戶的長、寬、厚為1.2 m×1.2 m×0.3 m，有2面墻（6 m×2.5 m）與其它房間相鄰，其余2面墻和屋頂均與室外相鄰。

2）房間圍護結構的材料

內、外墻均采用二四墻，屋頂設有防水層、保溫層，窗戶采用雙層玻璃、鋼質框架。

3）房間圍護結構參數

計算并查閱文獻[7]，確定房間維護結構參數如表1所示。

表1 房間圍護結構的參數Tab.1 Room envelope parameters

4）恒溫恒濕空調參數

恒溫恒濕空調的送風量Gs=5200 m3/h，則空調的換氣次數N=Gs/LWH=40次/h

[8]中的估算公式，通過計算得到特性參數 K=0.411、T=270 s、τ=27 s， 所以空調房間溫度的估算傳遞函數為

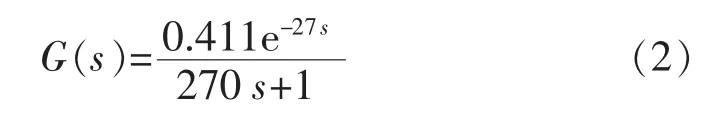
1.2 階躍響應辨識

獲取階躍響應的基本步驟：1）保持系統工作在初始穩態一段時間；2）快速改變系統的輸入量；3）記錄過程系統輸入輸出的變化曲線直至進入新的穩態。

1.2.1 內溫度數據采集平臺設計

選擇帶有SHT11溫濕度傳感器的TelosB節點采集室內環境的溫度數據。節點帶有一個基于IEEE 802.15.4/ZigBee協議、工作在2.4 GHz頻段的收發芯片CC2420。

基于ZigBee無線通信技術，搭建室內溫度數據采集平臺，建立了一個星型的無線網絡，如圖3所示。該網絡中，有1個協調器節點和6個終端節點。其中，協調器節點通過USB與上位機相連，主要作用是向終端節點發送溫濕度數據采集命令；然后協調器節點接收終端節點發送回來的溫濕度數據，并將此數據通過串口傳給上位機軟件，顯示并存入數據庫中。

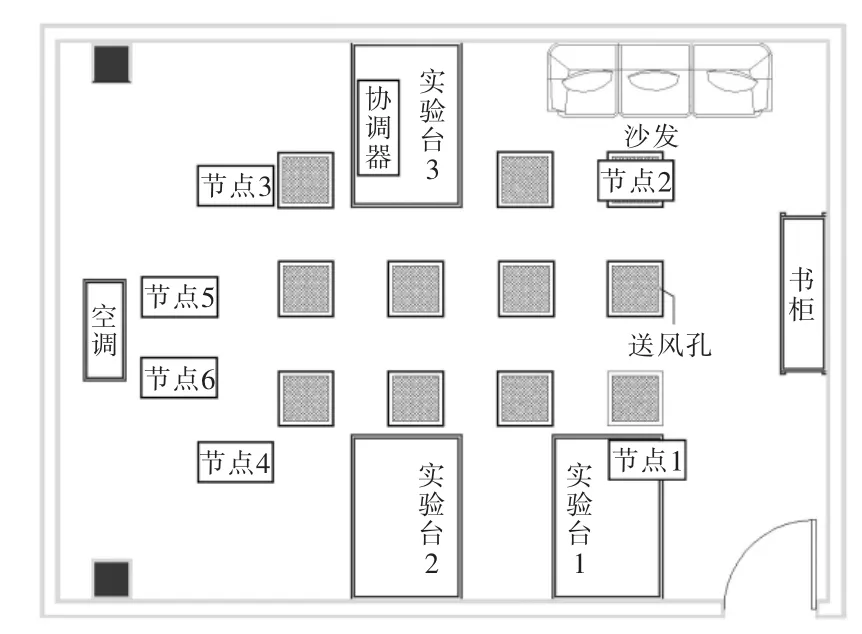
圖3 溫濕度測量節點分布示意圖Fig.3 Distribution schematic of the temperature and humidity measure-nodes

節點 1、2、3、4 的測量高度根據 ASHRAE 62-1989規定為1.8 m以下，又因為實驗研究的對象主要為坐姿，一般人坐姿高度在1.0～1.1 m，所有以離地1.1 m為監測高度，出風口處節點5、6距離出風口0.1 m，高度與出風口齊平。分別記錄，空調出風口溫度和空調房間的溫度。

1.2.2 實驗數據預處理

在曲線擬合之前必須對階躍響應獲得的實驗數據進行預處理，去除有明顯偏差的點以減少人為誤差，提高擬合的精度。

1）節點 1、2、3、4 數據的平均值為室內溫度，取節點5、6數據的平均值為空調送風口溫度。

2）i時刻室內溫度變化量ΔTi=Ti-T0

1.2.3 特性參數的獲取

保存處理好的實驗數據，并列出出風口溫度的階躍給定幅值與空調房間溫度的穩態值，如表2、表3所示。

表2 出風口溫度階躍給定幅值Tab.2 Given step value of air outlet （℃）

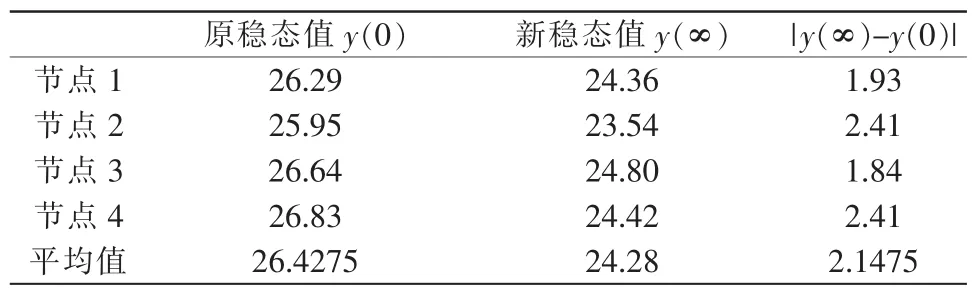
表3 空調房間溫度穩態值Tab.3 Stable value of air-conditioned room temperature（℃）

放大系數K按輸入輸出的穩態計算：K=［y（∞）-y（0）］/r=0.505。 對式（1）進行拉氏變換，得到系統的階躍響應：

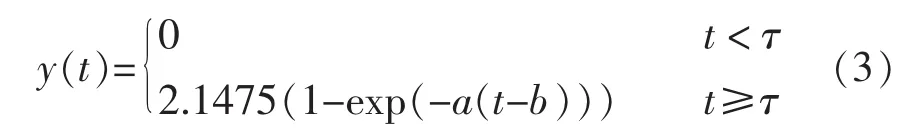
在MATLAB中利用最小二乘法進行曲線擬合，得：a=0.007777，b=28.94，sse：0.3323，rsquare：0.9799，adjrsquare：0.9796，rmse：0.0675

其中誤差平方和sse越接近0擬合效果越好，判定系數rquare（主要評價標準）越接近1越好，調整自由度后的判定系數adjrsquare越接近1越好，根的均方誤差rmse越接近0效果越好。由上述評價指標，可以看出擬合的效果很理想。

時間常數T=1/a、延時τ=b，根據擬合的結果，分別取T=129s，τ=29s，所以空調房間溫度的傳遞函數：

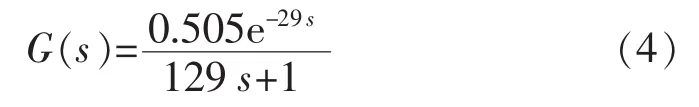
比較式（2）與式（4），可以發現本文方法與估算方法得到的模型并不相同。實際上該房間的送風方式不僅存在孔板下送風還有柵格側送風。時間常數T與經驗公式中的側面送風和散流器送風方式得到的時間常數T較為接近，但滯后時間τ與孔板送風方式得到的較為接近。

2 系統的仿真實現

由于單獨的PID控制不能在線修改參數Kp、Ki、Kd，難以滿足控制要求。簡單的模糊控制不具備積分環節，難以消除系統的穩態誤差。因此，本文綜合常規PID控制和模糊控制的優點，將2種控制結合起來構成模糊自適應PID控制。

在Simulink中建立系統的模塊化仿真模型，如圖4所示。其中，模塊“空調房間1”采用的是估算方法建立的模型，模塊“空調房間”采用的是本文方法建立的模型。

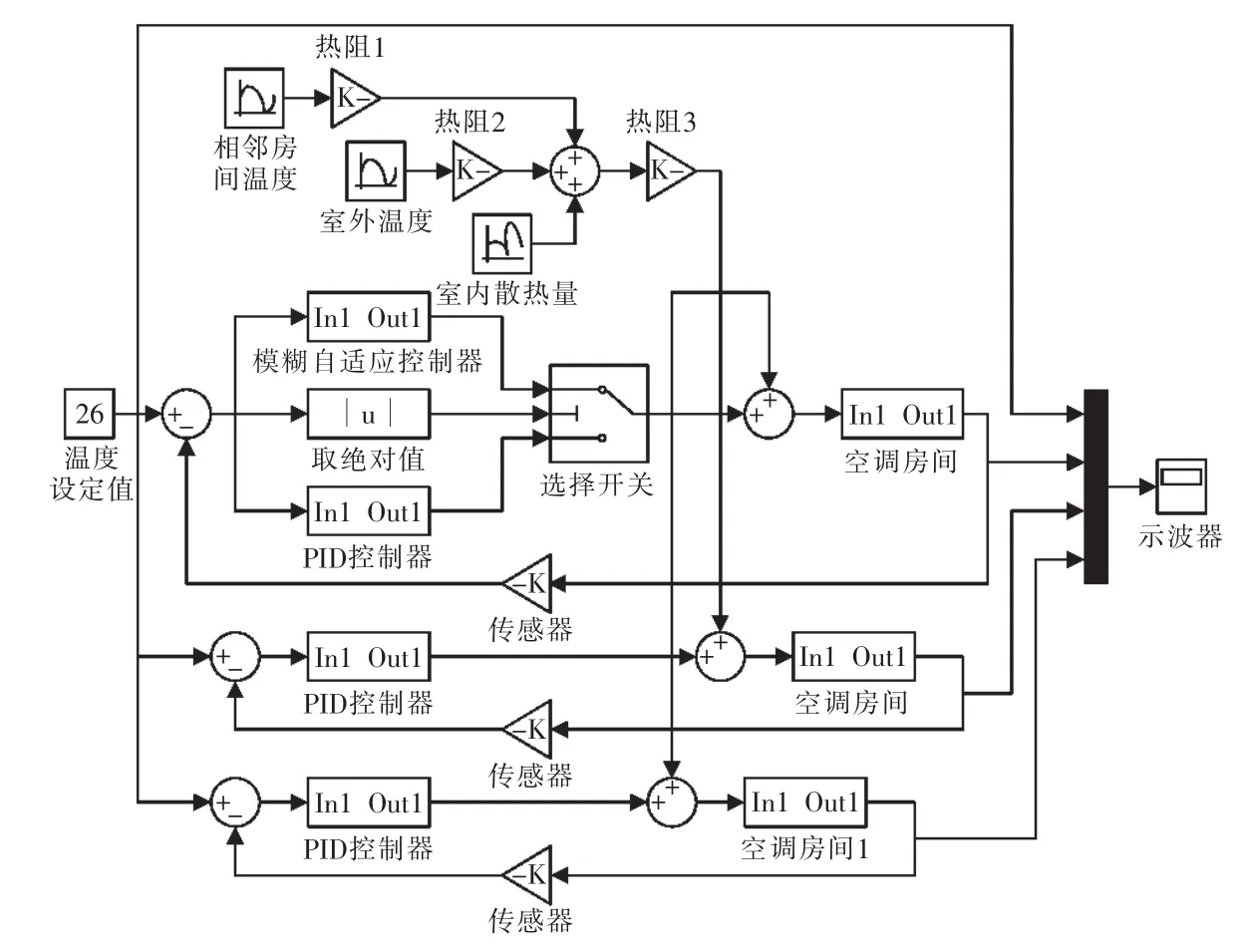
圖4 溫控系統仿真模型圖Fig.4 Schematic of temperature control system simulation model

對2種模型都進行常規PID控制仿真，仿真時間均取2500 s，溫度的設定初值為26℃，考察本文所建模型的優勢。

控制器選擇開關值取∣e∣=0.5℃，當∣e∣≥0.5℃時采用模糊控制；當∣e∣<0.5℃時采用常規PID控制。分別考察2種控制算法的響應時間、超調量與抗干擾能力等特性。

3 結果與分析

從圖4可以看出，空調房間的輸入由2部分組成：送風溫度以及室內外的干擾。熱阻1、熱阻2、熱阻3可由式（1）、（2）和表 1確定。 計算可知熱阻 1，熱阻2，熱阻 3 分別為 0.206W/℃，0.35W/℃，0.58 W/℃。 以合肥夏季氣候參數為例，相鄰房間溫度與室外溫度，分別取正弦函數[9]。隨機的室內干擾熱量參照人員、照明和設備的產熱指標分別為0.1 W/m2，20 W/m2，20 W/m2，實驗所用房間大約50m2，計算可得Q=230W。

系統的仿真曲線如圖5所示。

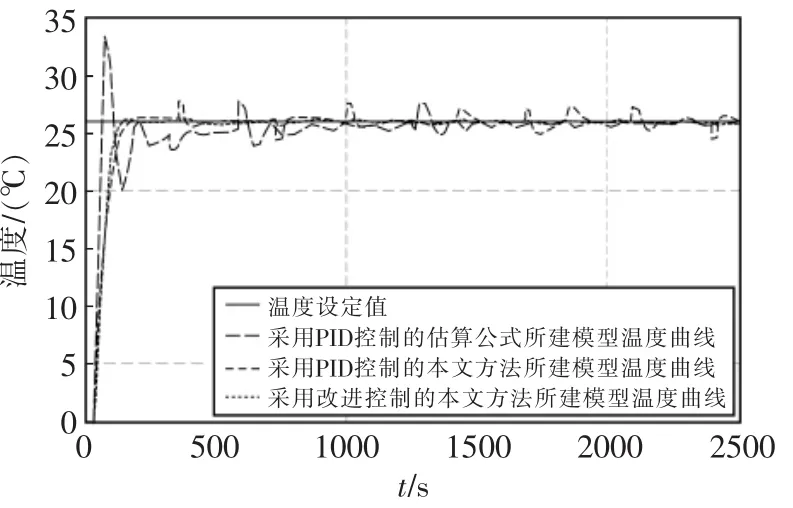
圖5 系統仿真曲線Fig.5 System simulation curve

仿真結果表明，采用估算公式所建模型的PID控制系統，從0℃上升到26℃的調節時間很長，系統很難保持在穩定狀態，過渡過程中存在較大的振蕩，抗干擾能力很差；采用本文方法所建模型的PID控制系統，從0℃上升到26℃的過渡時間約為353 s，盡管在控制過程中仍存在著超調，但幅度較小，最大超調只有1.8℃，此外，抗干擾能力也有一定的提高；采用本文方法所建模型的改進控制系統，從0℃上升到26℃的過渡時間僅用了194 s，在較短的時間內即可達到房間溫度設定值，系統的抗干擾能力很強，控制過程中，幾乎沒有出現超調，最大超調只有0.3℃。控制器能根據模糊規則庫在線調節，在快速性、穩定性、抗干擾等方面都優于常規的PID控制。

4 結語

上述分析表明，利用機理分析熟悉空調系統的工作機理和控制過程，模型具體參數通過階躍響應辨識獲取的方法是可取的。估算方法在建模研究時有很大的局限性，該方法不適用于復雜建筑結構；本文的建模方法具有普遍適用性，建模研究時不局限于規則建筑結構，也能適應于復雜建筑結構。此外，通過辨識獲取特性參數比直接用經驗公式計算更準確，更能反映實際。

采用常規控制的空調系統調節時間長、超調量大、穩定性差，控制過程中存在震蕩現象，這種現象不僅會縮短設備的使用壽命，同時也會消耗大量電能，造成浪費。此外，實際系統工作狀況復雜，被控對象的模型往往沒有仿真那樣理想，這種情況下，更需要對常規控制系統進行改進。改進后的控制系統根據模糊規則庫進行在線調節，實時修正參數Kp、Ki、Kd，縮短了系統的調節時間，減少了輸出超調量，增強了抗干擾能力。短時間內即可使室內溫度維持在設定值，避免了控制過程中大幅度震蕩，提高了設備的使用壽命，節約了電能的消耗，滿足了房間使用者的舒適性要求。

參考文獻：

[1]ISO-7730.Moderate Thermal Environment Determination of the PMV and PPD Indices and Specification of the Condition for Thermal Comfort[S].Geneva：International Standard Organization，1984.

[2]陳翠萍.一種基于PMV指標的空調節能方法研究[D].上海：東華大學，2011.

[3]段英宏.空調房間溫度預估模糊PID控制器的研究[J].系統仿真學報，2011，20（3）：620-622，626.

[4]張日楠，張九根，魏少翀.基于動態矩陣模糊PID算法的空調房間溫度控制[J].計算機測量與控制，2014，22（4）：1073-1075，1086.

[5]王亞峰.空調房間溫度模糊分數階PID控制器設計及其性能分析[D].蘭州：蘭州理工大學，2014.

[6]G Cherem-Pereira，N Mendes.Empirical modeling of room air conditioners for building energy analysis[J].Energy and Buildings，2012，47（5）：19-26.

[7]尉遲斌，盧士勛，周祖毅.實用制冷與空調工程手冊[M].北京：機械工業出版社，2011.

[8]施俊良.室溫自動調節原理和應用[M].北京：中國建筑工業出版社，1983.

[9]羅妤，吳堅，徐鑫晶.合肥市平均氣溫動態變化的非平穩時序分析[J].安徽農業大學學報，2013，40（6）：1059-1062.