基于強跟蹤UKF的室內目標跟蹤

張英坤

（1.河北省科學院應用數學研究所，石家莊 050081；2.石家莊開發區冀科雙實科技有限公司，石家莊 050081；3.河北省信息安全認證工程技術研究中心，石家莊 050081）

隨著無線通信技術、微型計算機技術和傳感器技術的快速發展，無線傳感器網絡[1-3]得到了廣泛應用，目標跟蹤[4-6]是其中一個重要的研究領域。在目標跟蹤領域，基于卡爾曼濾波理論[7-10]的目標跟蹤算法被應用于目標的狀態估計。UKF濾波算法[11-13]是非線性系統中常用的濾波算法，其狀態估計依賴于歷史數據，當測量數據存在偏差時，容易導致濾波效果變差甚至發散。本文在分析標準UKF算法的基礎上，利用強跟蹤思想[14]對其進行改進，并搭建了基于無線傳感器網絡的測試平臺，對強跟蹤UKF算法的性能進行了驗證。

1 實驗環境的搭建

利用麻省理工大學的Cricket系統搭建一個基于無線傳感器網絡的可用于室內目標跟蹤的實驗環境，如圖1所示。該網絡由4個Cricket節點構成，被跟蹤目標由機器人攜帶一個Cricket節點組成。Crieket節點利用射頻信號和超聲波脈沖之間的到達時間差來計算節點之間的距離。

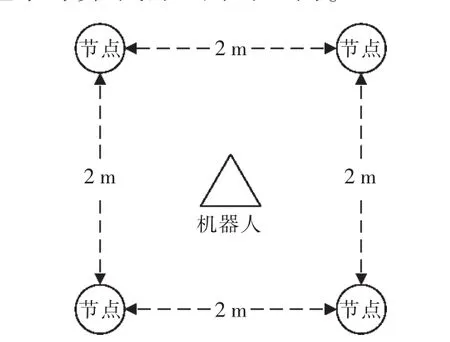
圖1 無線傳感器網絡Fig.1 Wireless sensor network

4個Cricket節點分布在已知的固定位置，同時發送射頻信號和超聲波脈沖，攜帶Cricket節點的機器人接收射頻信號，當接收到射頻信號后，啟動超聲波檢測器等待接收相應的超聲信號，檢測到超聲波脈沖時，利用射頻信號到達時間和超聲波脈沖到達時間之差來計算機器人與Cricket節點之間的距離。

2 系統模型的建立

本文研究的室內目標跟蹤屬于二維平面上的單目標跟蹤問題，其跟蹤過程可以描述如下：攜帶一個Cricket節點的機器人在4個Cricket節點構成的無線傳感器網絡中運動，根據機器人的運動方式建立機器人的系統模型，即狀態方程和觀測方程，再利用UKF算法迭代估計機器人的運動狀態，從而實現對機器人的跟蹤。下面給出機器人運動的狀態方程和觀測方程。

2.1 機器人運動的狀態方程

采用如下狀態方程來描述機器人的運動：

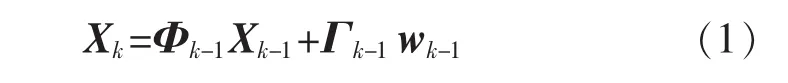
式中：Xk為機器人運動的狀態向量，（xk，yk）為 k 時刻機器人的位置坐標；為 k 時刻機器人在X、Y方向的速度；Φk-1為狀態轉移矩陣；Γk-1為過程噪聲輸入矩陣；wk-1為過程噪聲。

2.2 機器人運動的觀測方程

假設無線傳感器網絡中的節點具有相同的噪聲統計特性。當機器人在無線傳感器網絡中運動時，每個時刻均有4個節點檢測到信號。令表示 k時刻第i個節點測量到的自身與機器人之間的距離，將其作為觀測量，則有：

式中：（xi，yi）為第 i個節點的位置坐標。

3 基于強跟蹤的UKF算法

3.1 UKF濾波理論

3.1.1 無跡變換

UKF算法的關鍵步驟是無跡變換UT（unscented transform），UT變換是一種計算非線性變換中隨機變量數字特征的方法，其實現原理為在原先狀態分布中按某一規則取一些點，使這些點的均值和協方差等于原狀態分布的均值和協方差；將這些點帶入函數中，相應得到非線性函數值點集，通過這些點集求取變換后的均值和協方差，其Sigma點的選擇是基于先驗均值和先驗協方差矩陣的平方根的相關列實現的。具體計算方法如下：

（1）計算 2n+1個 Sigma點

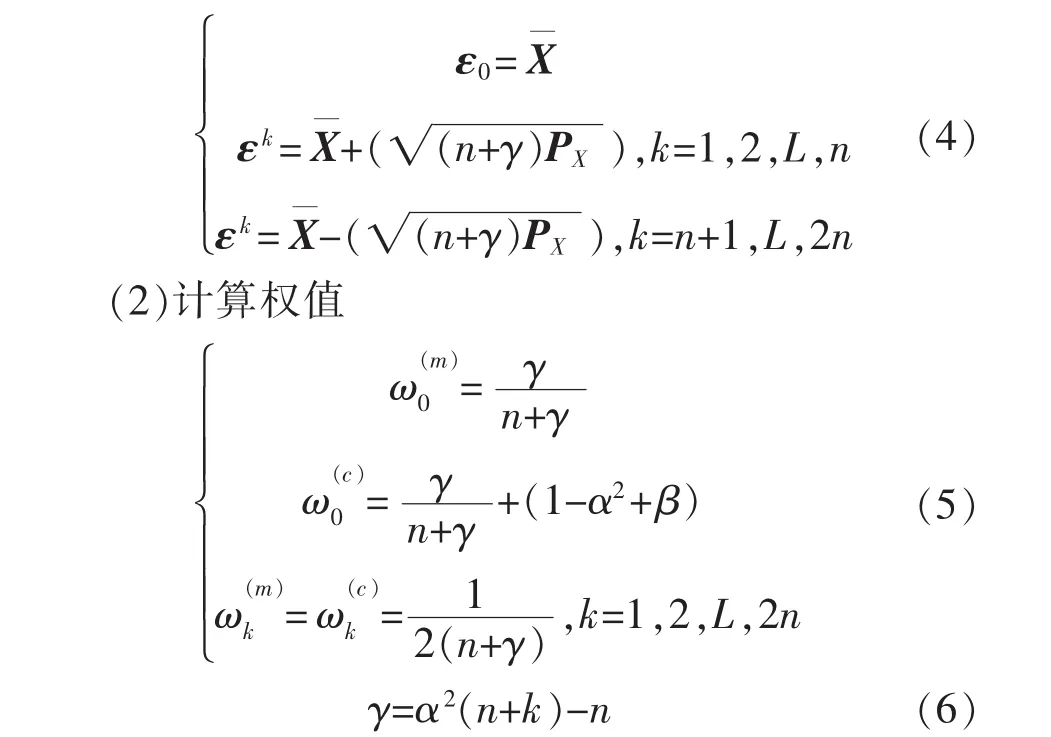
式中：n表示第n次采樣；α常取為一個小的正值，如0.001，它決定了采樣點相對于均值的分布情況；β為關于狀態變量分布的先驗知識在高斯分布時最佳取值為 2；γ為尺度調節因子；k通常取 0為均值的權值；為協方差的權值。

3.1.2 UKF濾波原理

考慮如下非線性模型：

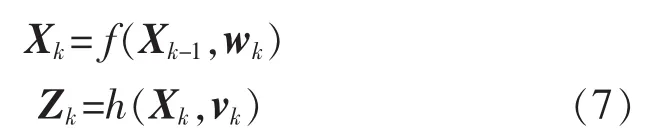
其中：Xk為狀態向量； f（·）為 n 維向量函數；hi（g）為m維向量函數；wk為過程噪聲項，為高斯白噪聲，服從 N（0，Qk）分布；Zk為觀測向量；vk為量測噪聲項，亦為高斯白噪聲，服從 N（0，Rk）分布。

則UKF濾波計算過程如下：

步驟1初始化k=1，計算狀態及協方差矩陣：

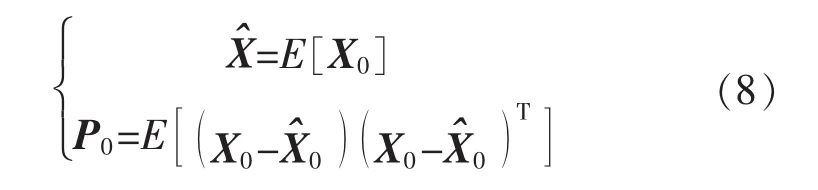
步驟2確定采樣點：

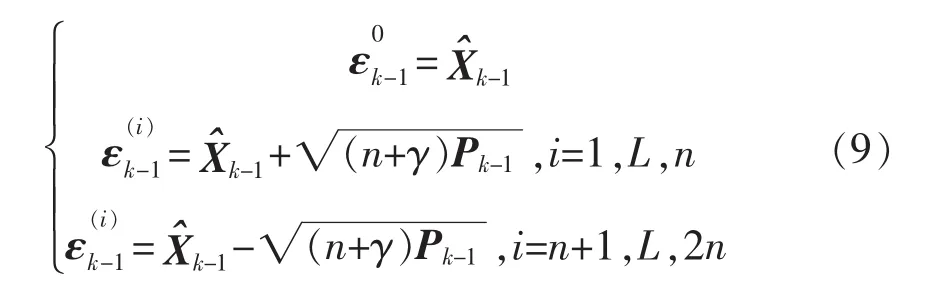
步驟3時間更新：

步驟4觀測更新：

步驟5濾波更新：

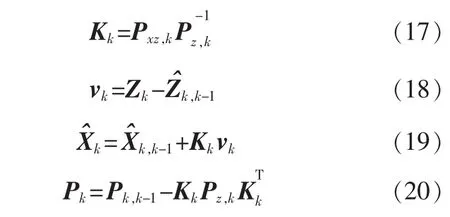
步驟6k=k+1，轉至步驟2重復計算。

3.2 強跟蹤濾波器對UKF的改進

強跟蹤的充分條件是選擇一個適合的時變增益矩陣Kk使得：

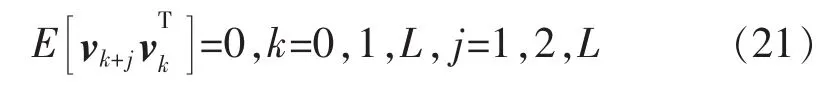
由于模型不確定性的影響，當濾波器的狀態估計值偏離系統狀態時，必然會在輸出新息序列的均值和幅值上表現出來。若在線調整增益陣Kk，強迫式（21）仍然成立，使得新息序列仍然保持正交，則可以強迫強跟蹤濾波器保持對實際系統狀態的跟蹤。強跟蹤濾波器對UKF的改進主要表現在通過實時調整狀態預報誤差的協方差矩陣和相應的增益矩陣來達到。因此修改式為

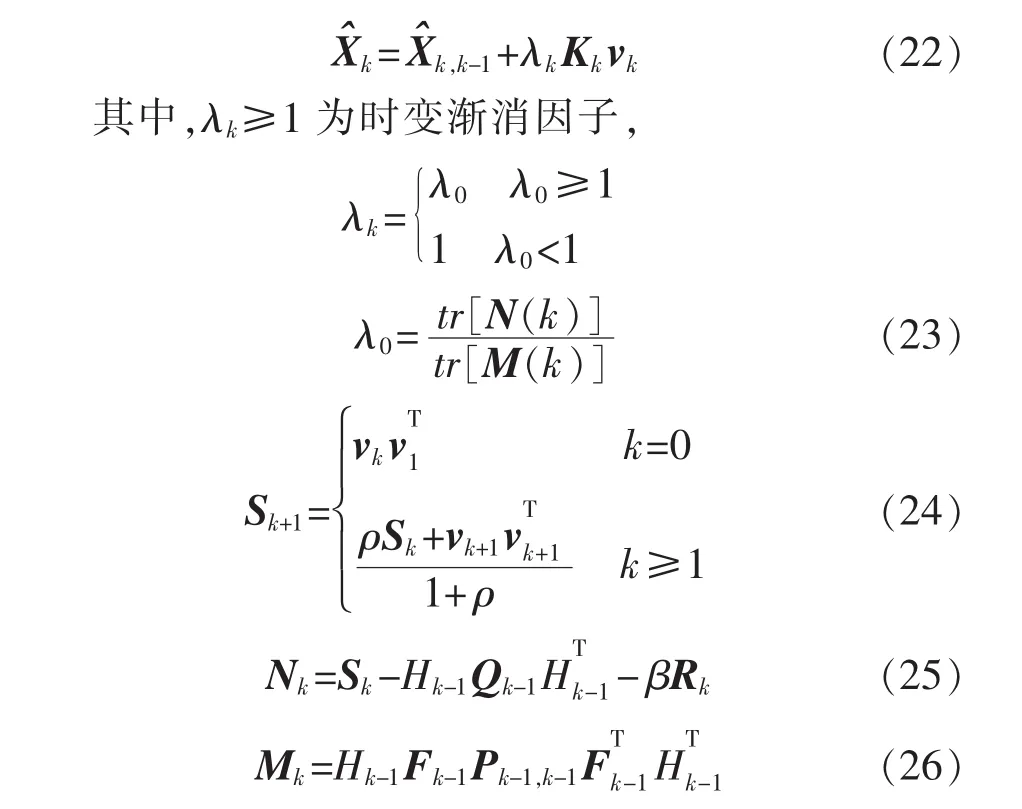
式中：0≤ρ＜1為遺忘因子，一般取 ρ=0.95；β≥1為一個選定的弱化因子，引入弱化因子的目的是為了使狀態估計值更加平滑，此數值可以根據經驗來設定，也可以通過計算機仿真來確定。

4 實驗及結果分析

為了驗證強跟蹤UKF算法的性能，將其應用于本文搭建的無線傳感器網絡中。機器人攜帶的節點每隔0.5 s發射一次射頻信號和超聲波脈沖，其他4個節點則檢測相應的射頻信號和超聲波脈沖，因此，采樣周期T=1 s。機器人沿著中心位于（100 cm，100 cm）、半徑為 50 cm的圓做勻速圓周運動，起始位置位于（150 cm，100 cm），角速度為則初始線速度近似為 （0 cm/s，8.73 cm/s）， 機器人的初始狀態為 X0=（150 cm，0 cm/s，100 cm，8.73 cm/s）。

在上述條件下，采用強跟蹤UKF算法與標準UKF算法的跟蹤結果如圖2、圖3和圖4所示。從圖2可以看出，強跟蹤UKF的跟蹤曲線相較于標準UKF更加接近于預定軌跡；圖3和圖4分別給出了X方向和Y方向的跟蹤誤差絕對值曲線。從中可以看出強跟蹤UKF的跟蹤精度要明顯優于標準UKF，且具有較好的魯棒性。

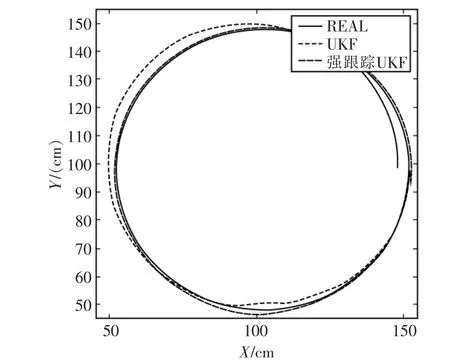
圖2 跟蹤軌跡曲線Fig.2 Tracking trajectory curve

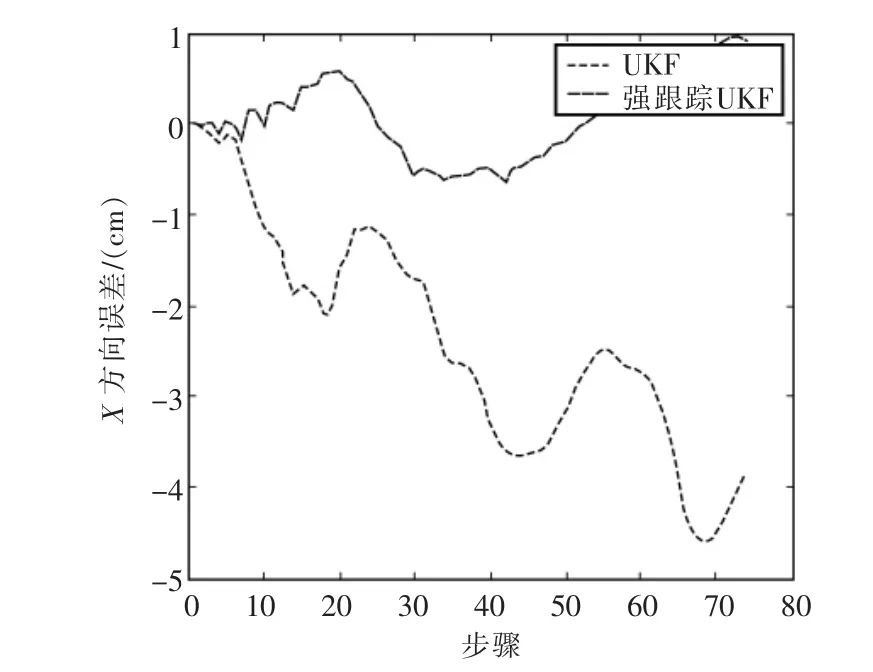
圖3 X方向誤差絕對值曲線Fig.3 Error absolute value curve of X direction

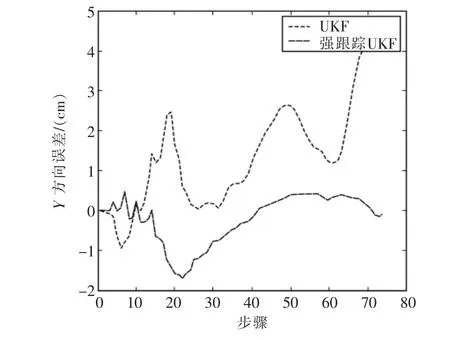
圖4 Y方向誤差絕對值曲線Fig.4 Error absolute value curve of Y direction

5 結語

為減少陳舊數據對目標跟蹤過程產生的不利影響，本文對標準UKF算法進行改進，利用強跟蹤思想修正協方差矩陣和相應的增益矩陣，搭建基于無線傳感器網絡的測試平臺對強跟蹤UKF算法的性能進行驗證，實驗結果表明，強跟蹤UKF算法具有更高的跟蹤精度，且魯棒性較好。

[1]張健，李鷗.改進的無線傳感器網絡TDOA定位算法[J].計算機工程與應用，2010，46（16）：117-120.

[2]馬靈芝.基于TDOA無線傳感定位算法的研究及應用[D].山東：山東大學，2012.

[3]孫大洋，錢志鴻，韓夢飛，等.無線傳感網絡中多邊定位的聚類分析改進算法[J].電子學報，2014，42（8）：1601-1607.

[4]權太范.目標跟蹤新理論與技術[M].北京：國防工業出版社，2009.

[5]薛皓.時間異步條件下的無線傳感器網絡目標跟蹤關鍵技術研究[D].北京：北京郵電大學，2009.

[6]侯杰虎.基于Kalman濾波器的視頻運動目標跟蹤算法研究[D].成都：成都理工大學，2012.

[7]付夢印，鄧志紅，張繼偉.Kalman濾波理論及其在導航系統中的應用[M].北京：科學出版社，2003.

[8]秦勤.雷達目標跟蹤的卡爾曼濾波方法的研究[D].大連：大連海事大學，2006.

[9]申逸.Kalman濾波技術在目標跟蹤中的應用研究[D].湖南：國防科學技術大學，2006.

[10]王思思，齊國清.自適應SCKF在機動目標跟蹤中的應用[J].電光與控制，2013，20（8）：6-10

[11]S Sarkka.On unscented Kalman filtering for state estimation of continuous-time nonlinear systems[J].IEEE Trans on Automation Control，2007，52（9）：1631-1641.

[12]劉慧霞，楊峰，梁彥.基于UKF的超視距雷達跟蹤算法研究[J].計算機測量與控制，2005，13（10）：1094-1096.

[13]任福君，張秀華，姜永成，等.改進UKF算法在移動機器人定位系統中的應用[J].哈爾濱工程大學學報，2012，33（10）：1289-1294.

[14]陳巴特爾，周東華.強跟蹤濾波器在倒立擺中的應用[J].控制工程，2012，19（1）：141-144.