基于狀態空間平均法的逆變器建模與控制策略研究

張 哲，專祥濤，于炎娟

（武漢大學 動力與機械學院，武漢430072）

隨著經濟的快速增長和科技的日新月異，電能作為工農業生產以及日常生活不可缺少的能源利用形式，各方面對其要求日益提高。電能質量作為衡量電能的重要指標[1]，其好壞直接關系到電網的安全、穩定運行。逆變器[2]作為新能源并網的接口，電網質量提高的凈化裝置[3]，不間斷電源系統的核心部件[4]，電力傳動與變頻電源的核心技術，近年來得到越來越多的關注，成為重要的研究課題。由逆變器為主要結構的功率調節裝置、無功補償裝置、動態電壓恢復器以及有源濾波器裝置等可以有效提高電能質量，提高電能利用率[5]。逆變裝置電壓輸出穩態誤差小、動態響應速度快、魯棒性強的優點依賴于逆變器主電路模型建立的準確性及控制系統設計的合理性。

本文利用狀態空間平均法建立了逆變器系統的模型并仿真驗證。結合實際要求，對逆變器主電路元器件進行設計，分析控制策略，選取雙環PI控制結構，并通過對穩態誤差、系統相位裕度和幅值裕度的分析，得到滿足條件的控制器參數的范圍[6]，結合實際情況選取合理的閉環參數。Matlab仿真結果驗證了本文建模分析的正確性和參數設計的有效性。本文提出的建模與控制策略的設計方法可以擴展到三相逆變器的建模與設計中。

1 主電路設計及參數選擇

根據實際情況，逆變器主電路各元器件參教設計要求如表1所示。

表1 逆變器設計要求Tab.1 Design requirements of inverter

綜合分析，本文選用電壓型單相全橋逆變系統作為主電路，原理如圖1所示，由AC/DC逆變電路和輸出整流濾波電路組成。

圖1 單相逆變器主電路結構圖Fig.1 Main circuit diagram of the single inverter

為輸出良好的正弦電壓波形，選取LC濾波器[7]消除開關頻率fk附高次諧波。其截止頻率fc遠小于開關頻率fk，可以有效地衰減高次諧波，其中截止頻率fc通常為開關頻率fk的1/10～1/5。在濾波電路中電感值越大，抑制諧波能力越強，但會增加電感質量、體積及低頻時的輸出阻抗，同時動態性能變差；電感值小，動態性能優越，但濾波性較差。同理，濾波電容的參數選取亦受諧波抑制能力與損耗以及動態性能的影響。綜合考慮，經計算濾波電感及電容參數選取如表2所示。

表2 主電路參數Tab.2 Main circuit parameters

2 基于狀態空間平均法的逆變器建模

單相逆變器的電路中含有非線性功率開關管，因此不能利用經典控制理論對電路進行分析設計，本文采用狀態空間平均法對電路進行線性化。

選取電感電流iL和電容兩端電壓Uo作為狀態變量，利用開關變量S線性化，即在開關周期Ts中，逆變器系統近似為線性系統。輸入電壓為直流電壓，在一個開關周期內，ui（t）可近似為開關周期平均值＜ui（t）＞Ts。同樣，忽略波紋，輸出電壓 uo（t）可近似為開關周期平均值＜uo（t）＞Ts。 經過小信號模型的線性化后其表達式為。得到單相逆變系統雙輸入單輸出的狀態空間平均方程如式（1）所示：

式中：iL為電感電流；uo為電容電壓；us為正弦調制波即電網電壓；Vcm為三角載波幅值；ui為直流輸入電壓；Ts為采樣周期。

由狀態空間平均模型推導出雙輸入Ui和io同時作用時系統復頻域輸出響應關系式為

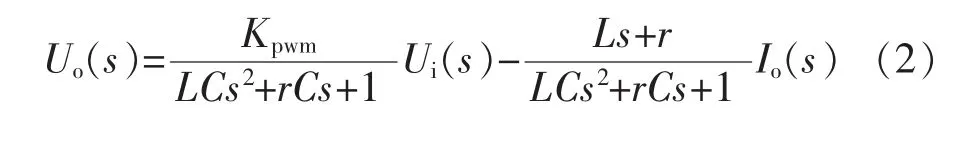
3 控制策略研究

本文根據系統未加控制器前的開環特性分析，選擇合適的控制策略與參數，綜合考慮采用帶輸出電流前饋的電感電流內環輸出電壓外環的雙閉環PI控制。

3.1 開環特性分析

由式（2）可知，逆變器的輸出電壓由逆變器空載輸出電壓和開環輸出阻抗2部分構成。空載諧振頻率為，阻尼比所以逆變器系統為阻尼很小的欠阻尼二階系統，空載時振蕩最劇烈，因此本文設計主要為空載狀態下的控制器。空載時系統的傳遞函教為

將相應器件參數代入，得到開環波特圖如圖2所示。

圖2 逆變器開環波特圖Fig.2 Inverter open loop bode figure

從圖2可以看出，系統相位裕度為0.0115 dB，處于臨界穩定狀態，因此需要加入控制器來提高系統穩態性能。

如圖3所示為逆變器開環輸出阻抗波特圖，從圖中可以看出輸出阻抗的幅值隨信號頻率的升高而增大。如果為非線性負載，諧波電流會在輸出阻抗上產生壓降，從而引起電壓畸變。

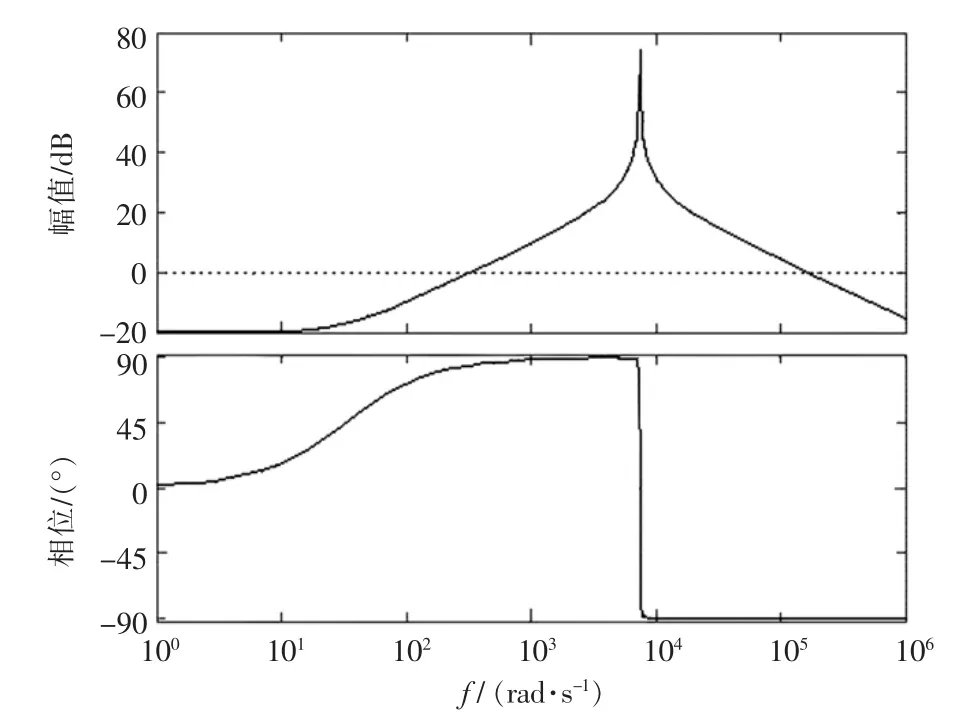
圖3 逆變器開環輸出阻抗波特圖Fig.3 Inverter open loop output impedance bode figure

3.2 控制方式選擇

逆變器系統控制方式分為單環控制和雙環控制。單環控制可以有效提高逆變器性能，但影響系統穩定性，并且對非線性負載抑制較差，易造成較大的電壓波動，因此在對控制性能要求較高的情況下不宜采用此種控制策略。

電感電流內環電壓外環控制中，電感電流內環相當于比例環節，在提高系統的穩定性的同時及時消除內環擾動，系統動靜態性能優于單環控制。電容電流反饋相當于輸出電壓的微分環節，有利于抑制輸出電壓波動，但系統穩定性變差。電感電流反饋穩定性優于電容反饋，且其對負載擾動抑制能力的不足可以通過加入電流前饋補償彌補。綜上所述，本文系統對系統穩定性要求較高，因此采用帶有輸出電流反饋的電感電流內環電壓外環控制，控制框圖如圖4所示。

圖4 帶輸出電流前饋的雙環PI反饋控制框圖Fig.4 Double loop PI control structure with output current feed forward control diagram

3.3 控制器設計

一般情況下，微分控制器會增強諧波分量輸出產生高次諧波，不利于系統穩定性，綜合考慮在此不使用微分控制，內環和外環均選用PI控制。為彌補電感電流反饋抗干擾能力不足，將輸出電流作為擾動加入輸出電流靜態前饋補償。利用極點配置的方法，設計電流控制器與電壓控制器為

本文采用極點配置控制器的設計方法，同時考慮內外環設計控制器，既簡化了設計過程，又避免內外環之間的相互影響，其中Kip=175，Kii=2562700，Kup=0.0301，Kui=99.8947。設計輸出電流的前饋控制時，不考慮輸出參考電壓的變化，可以得到輸出電流前饋補償器為Gff=1。

3.4 閉環特性分析

經計算得未加控制器時，電流內環開環傳遞函數為

根據式 （5）畫出未加控制器的電流內環波特圖，如圖5所示。從圖中可以看出，電流內環在低頻段是斜率為20 dB的直線，在高頻段為-20 dB的直線。系統存在靜態誤差，動靜態性能均較差，因此需加入電流環控制器 Gi（s）。

圖5 未加控制器時電流內環開環波特圖Fig.5 Bode figure of circuit inner open loop before adding controller

加入補償器后的電流環開環傳遞函數為

加入電流補償器后的電流環閉環傳遞函數為

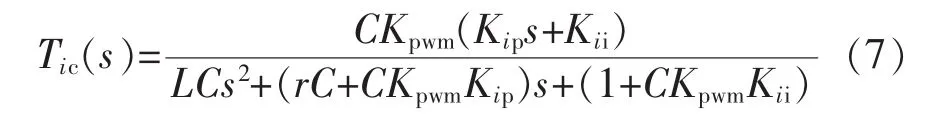
加入補償器后的電流環閉環波特圖如圖6所示。從圖6中可以看出，加入電流環后系統具有非常好的穩定性，電流環具有較寬的帶寬，系統快速性能較好。

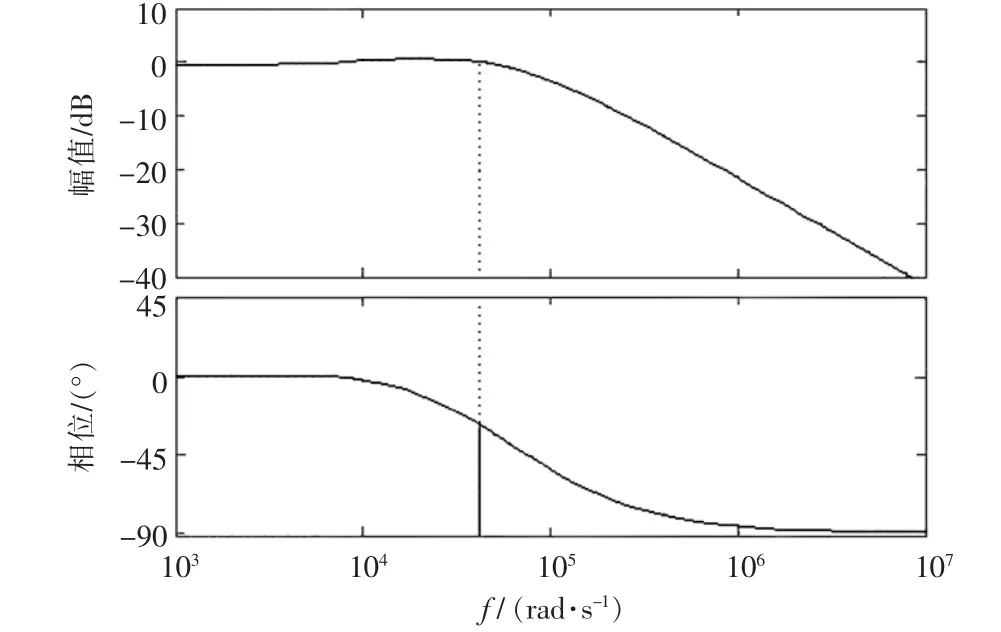
圖6 加入控制器后電流環閉環波特圖Fig.6 Bode figure of circuit inner close loop after adding controller

下面分析電壓環特性，未加控制器時，電壓環開環傳遞函數為

其波特圖如圖7所示。從圖中可以看出，其相位裕度為34.7°，穩定性能差，需加入控制器加以校正。

圖7 未加控制器時電壓環開環波特圖Fig.7 Bode figure of voltage open loop before adding controller

加入控制器后的電壓環開環傳遞函數為

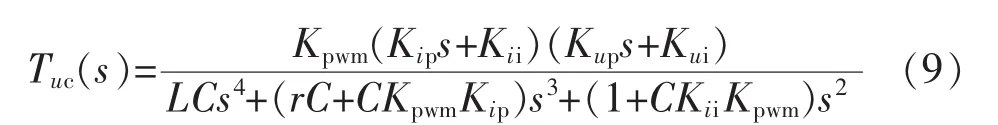
加入控制器后的電壓環閉環波特圖如圖8所示，且說明電壓環具有很好的穩定性。

圖8 加入控制器后電壓環閉環波特圖Fig.8 Bode figure of voltage close loop after adding controller

4 Matlab仿真與結果分析

4.1 穩態仿真

單相逆變器的額定功率Po為3 kW，輸出額定電壓為220 V/50 Hz的正弦波電壓，當負載為阻性時，額定功率下的阻性負載阻值為16.2 Ω。此時，輸出電壓與輸出電流的波形如圖9所示，與Simulink中FFT（快速傅里葉分析）對輸出電壓波形的諧波分析中輸出電壓的THD（總諧波電流畸變）為0.59%，諧波電壓較小，系統有較好的諧波抑制特性。

圖9 阻性負載滿載時輸出電壓電流波形圖Fig.9 Waveform figure of voltage and current in fully resistive load

當負載為阻性負載半載時，功率為額定功率的一半即Po=1.5 kW，此時阻性負載為32.4 Ω。輸出電壓電流波形如圖10所示，與輸出電壓的THD依然為0.59%，與阻性負載滿載時一致，因此功率變化對輸出電壓幾乎沒有影響。

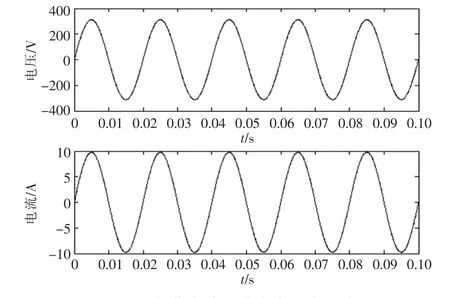
圖10 阻性負載半載時輸出電壓電流波形圖Fig 10 Waveform figure of voltage and current in half resistive load

當負載為阻感性與阻容性時，輸出電壓與輸出電流的波形如圖11、圖12所示。從圖中可以看出，阻感性時，電流相對于電壓有一定相位的超前；阻容性時電流相對于電壓有一定相位的滯后。無論負載為阻感性或阻容性，輸出電壓均能得到穩定的正弦波。

由上文分析可知，當單相逆變器穩定工作時，其輸出電壓能得到穩定的正弦波，能完全跟蹤輸出電壓給定值，因此系統具有非常好的穩態特性。

4.2 動態仿真

動態仿真主要分析當負載變化時的輸出電壓與電流波形。本文仿真突變均發生在電壓峰值時刻。輸出側有擾動的波形圖如圖13、圖14、圖15所示。

圖11 阻感性負載時輸出電壓電流波形圖Fig.11 Waveform figure of voltage and current in half resistive and inductive load

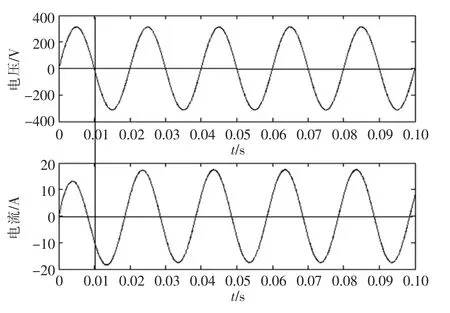
圖12 阻容性負載時輸出電壓電流波形圖Fig.12 Waveform figure of voltage and current in half resistive and capacitive load

圖13 阻性半載到滿載再到半載時的輸出電壓電流波形圖Fig.13 Waveform figure of voltage and current in half-fully-half resistive load

圖13為當負載從阻性半載到阻性滿載再到阻性半載時的輸出電壓、電流波形圖。從圖中可看出，當負載發生突變時，輸出電壓產生微小的畸變，且能快速恢復到正常工作情況，恢復時間約為0.5ms。

圖14 突加突卸滿負載輸出電壓電流波形圖Fig.14 Waveform figure of voltage and current in zero-fully-zero resistive load

圖14為對電路進行突加突卸滿負載時的仿真圖。從圖中可看出，當加載或卸載滿負載時，輸出電壓產生了畸變，也能很快憂復到正常工作情況，恢復時間約為1.5 ms。

圖15 突加突卸半額定功率負載輸出電壓電流波形圖Fig.15 Waveform figure of voltage and current in zero-half-zero resistive load

圖15為對電路進行突加突卸半額定功率負載時的仿真圖。從圖中可以看出，當加載或卸載半額定功率負載時，輸出電壓產生了畸變，但很快能恢復到正常工作情況，恢復時間約為0.8 ms。

從分析可知，當負載變化時，輸出電壓雖然產生微小畸變，但短時間內可以恢復，因此采用此控制器補償后的單相逆變器具有良好的動態性能及較強的抗負載擾動性。

當輸入電壓存在幅值為38 V、頻率為50 Hz的正弦波擾動時，輸出電壓的THD為0.54%，系統的輸入側抗擾動性能良好。

5 結語

本文通過對單相逆變器的研究，針對功率開關管導致的非線性問題，提出利用狀態空間平均法應用于單相逆變器建模的方法。利用Matlab驗證了所提出建模與控制策略的正確性和有效性。結果表明：帶輸出電流前饋的雙閉環PI控制策略可明顯改善系統的穩態性能與動態性能，其中內環電感電流反饋提高了系統的快速性，外環輸出電壓瞬時值反饋提高了系統輸出的穩定性。由此設計的控制策略，可廣泛運用于電源設計、分布式能源并網、變頻器等設備。

[1]程浩忠，艾芊，張志剛，等.電能質量[M].北京：清華大學出版社，2006.

[2]周志敏，周紀海，紀愛華.逆變電源使用技術—設計與應用[M].北京：中國電力出版社，2005.

[3]劉聰，戴珂，張樹全，等.用并網逆變器實現有源濾波與無功補償功能的研究[J].大功率變流技術，2001（6）：34-38.

[4]Gueldner H，Wolf H，Blacha N.Single phase UPS inverter with variable output voltage and digital state feedback control[J].IEEE International Symposium on Industrial Electronics，2001，2（6）：1089-1094.

[5]王兆安，劉進軍.電力電子技術[M].北京：機械工業出版社，2010.

[6]Ahmed K H，Massoud A M，Finney S J，et al.Optimum selection of state feedback variables PWM inverters control//[C].PEMD’08，York，2008：125-129.

[7]Komurcugil H.Steady-state analysis and passivity-based control of single-phase PWM current-source inverters[J].IEEE Transactions on Industrial Electronics，2010，57（3）：1026-1030.