基于神經網絡PID控制算法的自動調平系統的仿真研究
李 楠,吳玉厚
(沈陽建筑大學 機械工程學院,遼寧 沈陽 110168)
0 引言
隨著我國建筑業的發展,國家對高空作業平臺的安全性的重視程度有很大提高,因此本文對經典PID 控制算法和神經網絡PID 控制算法進行了分析比較,突出神經網絡PID 控制算法在穩定性、快速性、準確性的優點。
1 經典PID 控制器
在工業控制系統中,經典PID 控制是應用最為廣泛的控制算法,其控制算式為:

PID 控制算法要采用離散化控制算法。表達式為:

式中:KP,KI,KD的分別為比例系數、積分系數、微分系數e(k)為第k 次,采樣的輸入偏差u(k)為第k 次采樣的系統輸出。
2 神經網絡控制
BP 神經網絡是一種前向網絡,典型BP 神經網絡包含輸入層輸出層和隱含層三層網絡。如圖1 所示。輸入層節點傳遞輸入信號到隱含層,隱含層神經元的傳遞函數常取可微的單調遞增函數,整個網絡神經元的特性由輸出層神經元的的特性決定。

圖1 三層BP 網絡結構圖
設x1,x2,…,xn為BP 網絡的輸入;y1,y2,…,yn為輸出;wji1為輸入層到隱含層的連接權值;wji2為隱含層到輸出層的連接權值。
輸入層:xi=xi0
3 自動調平控制系統的組成

圖2 自動調平控制系統的組成
本文采用的自動調平控制系統主要由神經網絡PID控制器,被控對象(高空作業平臺)和雙軸傾角傳感器組成。控制器部分由常規PID 控制器和神經網絡控制器組成,PID 控制器必須調整好比例,微分,積分的關系,使被控量相互配合相互制約以取得較好的控制效果。如圖2 所示。
經典的PID控制器直接對被控對象進行閉環控制,并且三個參數KP、KI、KD是在線調整方式,神經網絡根據系統的運行狀態調節PID 控制器的參數,以其達到某種性能指標的最優化。
神經網絡PID 控制算法歸納如下:①確定輸入節點數和隱含層節點數,并賦予各層加權系數的初值,選定學習速率和慣性系數,并令k=1;②采樣的到r(k)和y(k),并計算出e(k);③計算各神經網絡的輸入和輸出,輸出層為三個可調參數KP、KI、KD;④計算PID 控制器的輸出;⑤進行神經網絡學習,在線調整加權系數,實現KP、KI、KD的自適應調整;⑥令k=k+1 返回①。
被控對象為三吊點懸吊式高空作業平臺,調平策略采用同向追逐式調平法,即上升過程中最高點不動,通過雙軸傾角傳感器測出x 軸,y 軸與水平面夾角,然后依次調平;下降過程中最低點不動,通過雙軸傾角傳感器測出x 軸,y 軸與水平面夾角,然后依次調平。采用此方法大大提高了調平精度。
4 控制系統的仿真
本系統仿真時間為6s,采樣時間為0.01s 神經網絡PID 和PID 的初始控制參數為KP'=4.7787、KI'=1.2391、KD'=0.269 學習速率η=0.28,慣性系數α=0.04。
為分析系統的時域性能,對系統輸入單位階躍信號,通過仿真結果(圖3,圖4)可以看出,采用神經網絡PID 算法在系統的上升時間峰值時間調節時間和超調量以及穩態誤差等各項指標都比經典PID 控制算法要好,跟蹤能力也優于經典PID,采用神經網絡PID 的響應時間在0.5s 內振蕩次數少于經典PID 控制算法,使用神經網絡PID 算法后系統的時域性能有很大提高。
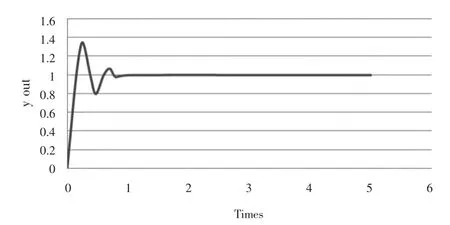
圖3 PID 控制仿真結果

圖4 神經網絡PID 控制仿真結果
5 結束語
驗證了自動調平系統采用神經網絡PID 控制的可行性和優點,在實際應用中對比例、微分、積分參數,可以進行自適應調整,加強了系統的響應特性。
[1]劉軍.電動吊籃使用過程中應著重控制的幾個環節[J].建筑安全,2002,5.
[2]李美芳,陸衛倩,王琰.ZLD2-B 型微電腦外墻高空吊籃的設計[J].機械制造,2004.
[3]黃向華.控制系統仿真[M].北京:北京航空航天大學出版社,2008.
[4]Passino KM.Bridging the gap between conventional and intelligent control.IEEE Control Systems Magazine,1993,3.
[5]BennettS. The past of PID controllers.Annual Reviews in Control,2001,25.

