兩電機(jī)變頻系統(tǒng)神經(jīng)網(wǎng)絡(luò)逆PID的控制

張錦，高磊，仲偉松

（宿遷學(xué)院，江蘇宿遷　223800）

兩電機(jī)變頻系統(tǒng)神經(jīng)網(wǎng)絡(luò)逆PID的控制

張錦，高磊，仲偉松

（宿遷學(xué)院，江蘇宿遷223800）

由于兩電機(jī)變頻系統(tǒng)非線性強(qiáng)耦合性，先搭建由神經(jīng)網(wǎng)絡(luò)辨識原系統(tǒng)的廣義逆模型，再與原系統(tǒng)串聯(lián)，從而構(gòu)成復(fù)合偽線性系統(tǒng)，使系統(tǒng)解耦線性化。然后引入PID控制以提高系統(tǒng)的魯棒穩(wěn)定性。實(shí)驗(yàn)結(jié)果表明，此方法不僅較好地實(shí)現(xiàn)了系統(tǒng)的解耦，而且魯棒穩(wěn)定性較強(qiáng)。

神經(jīng)網(wǎng)絡(luò)逆；兩電機(jī)變頻系統(tǒng)；解耦

0　引言

多電機(jī)同步控制系統(tǒng)在現(xiàn)代工業(yè)生產(chǎn)中應(yīng)用廣泛，高性能的多電機(jī)同步調(diào)速系統(tǒng)可有效提高產(chǎn)品品質(zhì)及經(jīng)濟(jì)效益。目前我國以速度與張力為控制對象的同步調(diào)速系統(tǒng)多為直流傳動方式，直流傳動控制簡單，調(diào)速性能良好，但存在制造及維護(hù)成本高，容量小等缺陷。隨著電力電子技術(shù)及計算機(jī)控制技術(shù)的高速發(fā)展，多臺交流電機(jī)同步控制性能逐漸提高，其結(jié)構(gòu)簡單且制造及維修成本低，但這類控制的高階、非線性、強(qiáng)耦合問題如何解決是當(dāng)前研究的瓶頸［1］。

逆系統(tǒng)的出現(xiàn)為解決這類控制問題提供一條有效途徑。但該方法要求模型精確可知，按照傳統(tǒng)逆系統(tǒng)方法得到這類非線性系統(tǒng)的數(shù)學(xué)模型較困難。因此有學(xué)者提出基于神經(jīng)網(wǎng)絡(luò)［2］構(gòu)建逆系統(tǒng)的方法來解決此問題。神經(jīng)網(wǎng)絡(luò)具有自學(xué)習(xí)、自適應(yīng)等功能，可以做到不依賴被控對象的數(shù)學(xué)模型，具有較強(qiáng)的適應(yīng)能力和實(shí)時性，用這種方法可以有效解決逆系統(tǒng)模型中建模困難等問題。因此使用神經(jīng)網(wǎng)絡(luò)辨識由多電機(jī)變頻系統(tǒng)構(gòu)成的原系統(tǒng)，串聯(lián)于原系統(tǒng)前，從而構(gòu)成復(fù)合偽線性系統(tǒng)，完成了系統(tǒng)的解耦與線性化。由于在構(gòu)建過程中難免會出現(xiàn)一些建模誤差，所以選擇PID控制器［3］以確保系統(tǒng)的魯棒性。

本文以兩電機(jī)變頻調(diào)速系統(tǒng)為研究對象，將廣義逆辨識兩電機(jī)控制系統(tǒng)方法與PID控制相結(jié)合，并以多電機(jī)變頻系統(tǒng)實(shí)驗(yàn)平臺進(jìn)行實(shí)驗(yàn)研究。

1　兩電機(jī)變頻系統(tǒng)數(shù)學(xué)模型

圖1為兩電機(jī)變頻同步調(diào)速系統(tǒng)轉(zhuǎn)速與張力控制結(jié)構(gòu)示意圖。

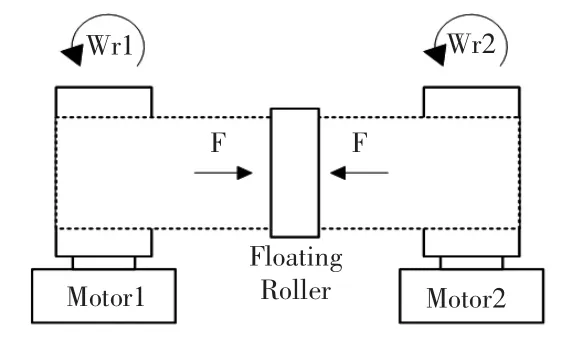
圖1　兩電機(jī)變頻系統(tǒng)結(jié)構(gòu)示意圖Fig.1 Control diagram of two-motor variable frequency system

基于矢量控制方式下且磁通穩(wěn)定時，其數(shù)學(xué)模型可簡化為［4］：

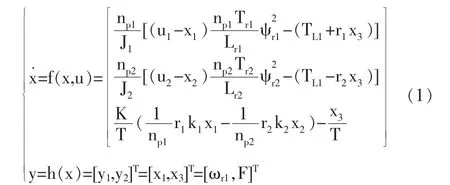
式中：下標(biāo)1、2分別表示第1、2臺電機(jī)。k，r分別為皮帶輪的速比、半徑；J—轉(zhuǎn)子轉(zhuǎn)動慣量；ω—定子頻率的同步角速度；TL—負(fù)載轉(zhuǎn)矩；Tr—電磁時間常數(shù)；ψr—為轉(zhuǎn)子磁鏈；Lr—轉(zhuǎn)子自感；ωr—電氣角速度；K—傳遞函數(shù)；T—張力變化常數(shù)；np—電機(jī)的極對數(shù)；F—皮帶的張力。其中狀態(tài)變量控制變量為

2　系統(tǒng)廣義逆的實(shí)現(xiàn)

將式（1）中輸出求導(dǎo)，得其Jacobi矩陣為：

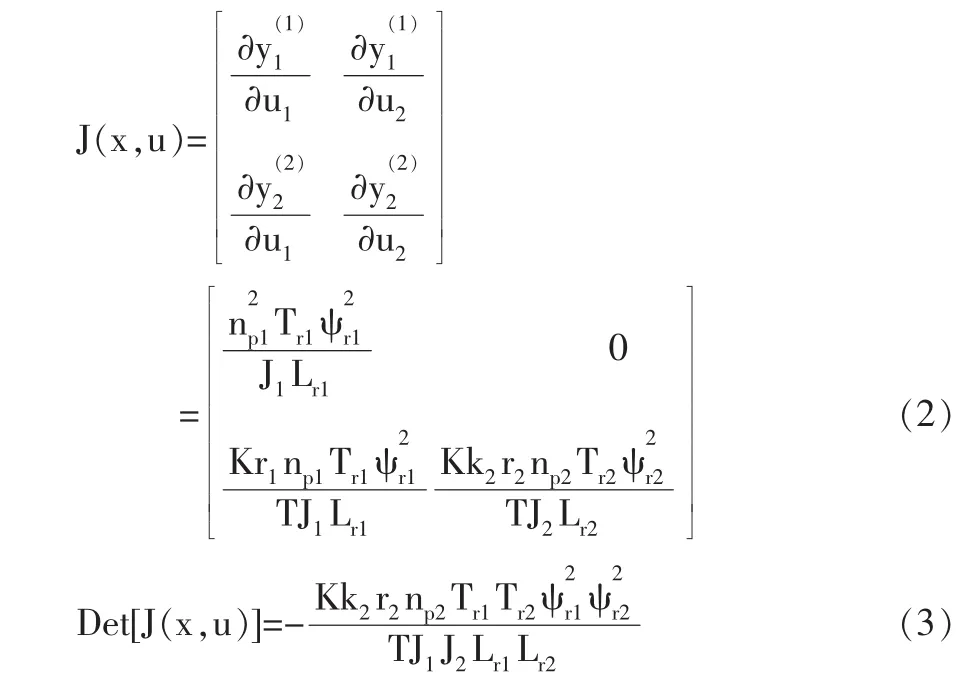
根據(jù)廣義逆理論［5］，系統(tǒng)的向量本階性為3，而系統(tǒng)的相對階為a=（1，2），即階數(shù)為a1+a2=3，因此系統(tǒng)的本階性等于向量相對階，可知此系統(tǒng)可逆。由此系統(tǒng)的廣義逆可表示為：

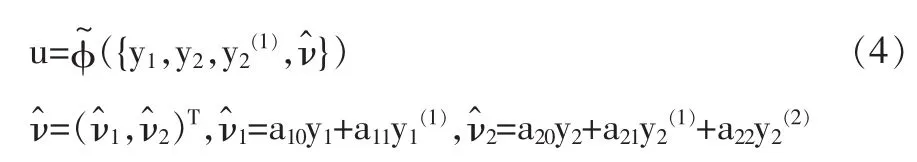
其中：a10=1，a11=1；a20=1，a21=1.414，a22=1。將廣義逆系統(tǒng)與兩電機(jī)變頻系統(tǒng)串接，即構(gòu)成廣義偽線性復(fù)合系統(tǒng)，其輸入輸出傳遞函數(shù)為：

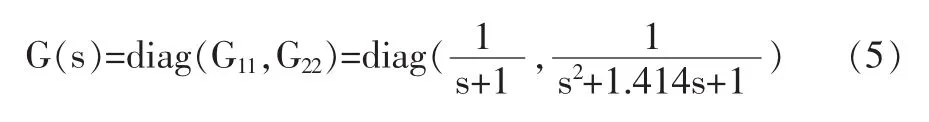
3　神經(jīng)網(wǎng)絡(luò)廣義逆PID控制策略

首先構(gòu)建由神經(jīng)網(wǎng)絡(luò)辨識的原系統(tǒng)（兩電機(jī)變頻系統(tǒng)）廣義逆模型：①向原系統(tǒng)給定足夠的激勵信號；②取原系統(tǒng)的輸出作為神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)的輸入，而原系統(tǒng)輸入作為神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)的輸出，并對采樣信號進(jìn)行歸一化處理；③神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)采用5-10-2的3層BP網(wǎng)絡(luò)。中間層傳函采用tansig，輸出層傳函采用purelin，學(xué)習(xí)函數(shù)采用梯度遞減訓(xùn)練函數(shù)traingdx，判斷誤差收斂趨勢是否符合要求。

將由神經(jīng)網(wǎng)絡(luò)逼近的廣義逆模型與以兩電機(jī)同步系統(tǒng)為構(gòu)成的原系統(tǒng)串接，從而行成復(fù)合偽線性系統(tǒng)。由式（5）可知，原系統(tǒng)轉(zhuǎn)化為1/（s+1）的速度子系統(tǒng)及1/（s2+ 1.414s+1）的張力子系統(tǒng)。

轉(zhuǎn)化后的偽線性系統(tǒng)實(shí)現(xiàn)了原系統(tǒng)的解耦與線性化，但由于存在開環(huán)建模誤差，此時引入PID控制從而取得更好的閉環(huán)控制效果。確定最佳PID參數(shù)后，從而構(gòu)成了神經(jīng)網(wǎng)絡(luò)逆PID閉環(huán)控制系統(tǒng)。如圖2所示。

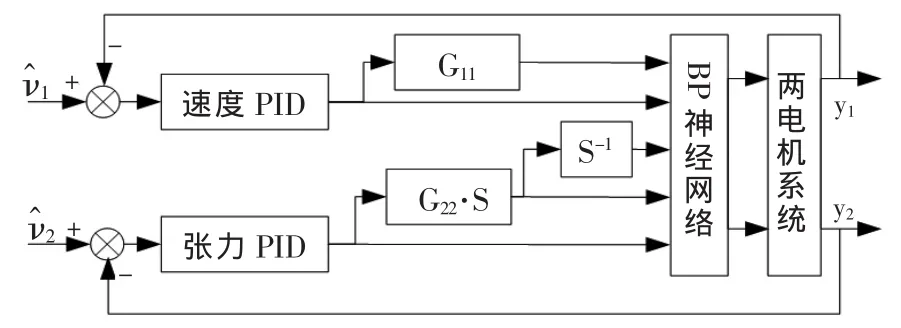
圖2　神經(jīng)網(wǎng)絡(luò)逆PID控制原理圖Fig.2 Diagram of NNGI-PID control system

4　實(shí)驗(yàn)研究

圖3所示為多電機(jī)變頻系統(tǒng)試驗(yàn)平臺。本文以其中2臺電機(jī)為研究對象。試驗(yàn)平臺包括上位機(jī)監(jiān)控軟件WinCC，S7-300PLC及SM335高速模擬量輸入模塊，F(xiàn)M350高速計數(shù)器模塊，SL100型張力傳感器，及光電編碼器，2臺MMV變頻器，2臺2.2 kW的三相異步電機(jī)。

圖3　多電機(jī)變頻系統(tǒng)試驗(yàn)平臺Fig.3 Experiment platform of multi-motor variable frequency systems

為了使原系統(tǒng)穩(wěn)定先設(shè)計PID控制器，接著速度給定為200～600 r/min的隨機(jī)方波，張力給定為200～600 N的隨機(jī)方波，然后在PLC中構(gòu)建神經(jīng)網(wǎng)絡(luò)以逼近原系統(tǒng)的廣義逆，組成神經(jīng)網(wǎng)絡(luò)廣義逆系統(tǒng)，最后引入PID算法以消除建模及穩(wěn)態(tài)誤差。

試驗(yàn)結(jié)果如圖4～5所示。傳統(tǒng)PID控制，速度在突變時，張力存在較大波動。而采用神經(jīng)網(wǎng)絡(luò)廣義逆PID控制時，張力受速度突變影響較小，較好地實(shí)現(xiàn)了張力與速度的解耦。

5　結(jié)束語

圖4傳統(tǒng)PID控制時系統(tǒng)實(shí)測響應(yīng)波形
Fig.4 Measured responses with conventional PID control

由神經(jīng)網(wǎng)絡(luò)構(gòu)建的廣義逆模型與PID相結(jié)合的控制方法。經(jīng)過多電機(jī)變頻系統(tǒng)試驗(yàn)平臺研究，可得出如下結(jié)論：

（1）由感應(yīng)電機(jī)組成的兩電機(jī)變頻系統(tǒng)速度與張力的耦合性很強(qiáng)，傳統(tǒng)PID可一定程度上緩解系統(tǒng)耦合問題，但耦合度依然很大。

（2）對比傳統(tǒng)PID方法，神經(jīng)網(wǎng)絡(luò)逆PID控制具有更好的魯棒穩(wěn)定性。

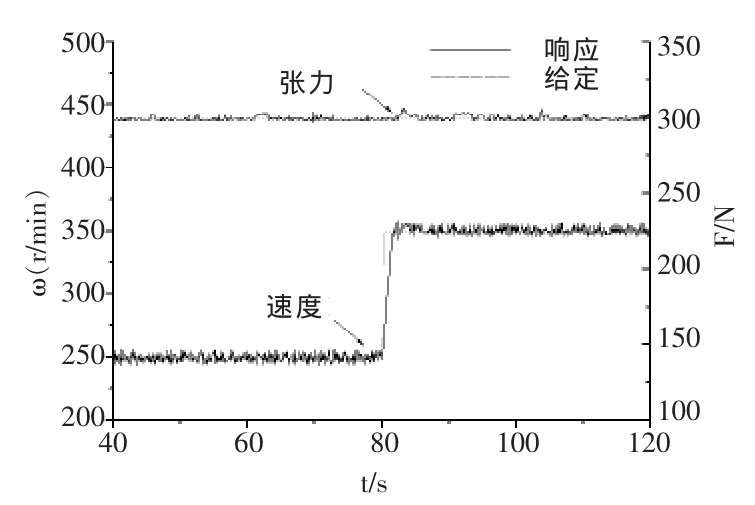
圖5　神經(jīng)網(wǎng)絡(luò)廣義逆PID控制時系統(tǒng)實(shí)測響應(yīng)波形Fig.5 Measured responses with NNGI-PID

［1］李春文，馮員錕.多變量非線性控制的逆系統(tǒng)方法［M］.北京：清華大學(xué)出版社，1991.

［2］朱大奇.人工神經(jīng)網(wǎng)絡(luò)研究現(xiàn)狀及其展望［J］.江南大學(xué)學(xué)報，2004，1.

［3］王偉，張晶濤，柴天佑.PID參數(shù)先進(jìn)整定方法綜述［J］.自動化學(xué)報，2000，3.

［4］張懿，劉國海，魏海峰，等.基于最小二乘支持向量機(jī)左逆的兩電機(jī)變頻調(diào)速系統(tǒng)張力辨識策略［J］.中國電機(jī)工程學(xué)報，2010，30.

［5］劉國海，張錦，趙文祥，等.兩電機(jī)變頻系統(tǒng)的支持向量機(jī)廣義逆

Neural Network Generalized Inverse Based on Two-motor Variable Frequency System PID Applications

ZHANG Jin，GAO Lei，ZHONG Wei-Song
（School of Suqian College，Suqian Jiangsu 223800，China）

Due to the nonlinear heavy-coupling characteristic in two-motor variable frequency systems，the generalized inverse model of original system is approximated by neural network firstly，then the pseudo-linear system is formulated by integrating the original system with this model，and the system's decoupling linearization are achieved.Then the robustness can be improved by means of the PID controllers. The experimental results show that the control strategy has good decoupling performance and can deal with external disturbances with strong robustness.

neural network generalized inverse（NNGI）；two motor variable frequency systems；decoupling

TH-39

A

10.3969/j.issn.1002-6673.2015.06.045

1002-6673（2015）06-126-03

2015-09-28

宿遷學(xué)院科研基金項(xiàng)目（2014KY09）；江蘇省自然科學(xué)基金項(xiàng)目（BK20140586）

張錦（1986-），男，碩士研究生，助教。從事電機(jī)控制技術(shù)方面研究。