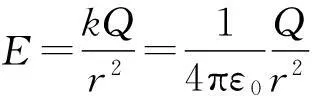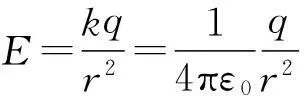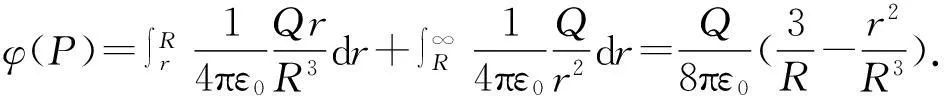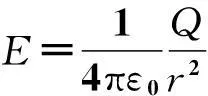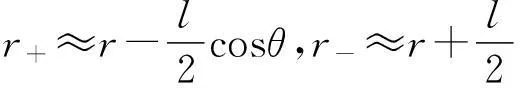帶電體的電勢及場強求解方法
黃開智
(江蘇省姜堰二中,江蘇 泰州 225500)
帶電體的電勢及場強求解方法
黃開智
(江蘇省姜堰二中,江蘇泰州225500)
摘要:本文探討了均勻帶電球體和球殼周圍的電勢及電場強度分布情況,并通過Mathematica軟件模擬了等量異種電荷電勢的三維分布,總結了幾種典型的帶電體的電勢及其場強的計算方法.
關鍵詞:電勢;電場強度;高斯定理;Mathematica軟件
在電磁學的習題中常會遇到求解帶電體模型的電勢或者場強的問題,例如均勻帶電球殼、均勻帶電球體、等量異種或同種點電荷等模型.高中階段,學生很難分清楚電勢與電場強度的概念及其計算方法,僅能勉強求解一些比較特殊點的電勢或者電場強度.經驗不足的教師也不大清楚典型帶電體周圍電勢的變化情況,導致不能站在一個更高的角度來施教.
靜電場中某點的電勢在數值上等于單位正電荷在該點處的電勢能,也等于單位正電荷從該點經過任意路徑移到無限遠處時電場力所做的功(此時認為無窮遠處電勢為零).若已知電荷在空間的分布,一般來說求電勢或場強的方法有兩種,可根據不同電荷分布,選擇不同方法:一種是先求解出電場強度E的分布函數,應用場強與電勢的關系,對場強做線積分運算,求解電勢;另一種是直接根據電勢疊加原理,求解任意點的電勢,進而運用電勢梯度的負值等于場強的特點求解該點場強.
1均勻帶電球體的場強及電勢分布
問題:均勻帶正電球體置于真空中,帶電量為Q,球體半徑為R,球心為O,求球體周圍空間的電場強度及電勢.

圖1
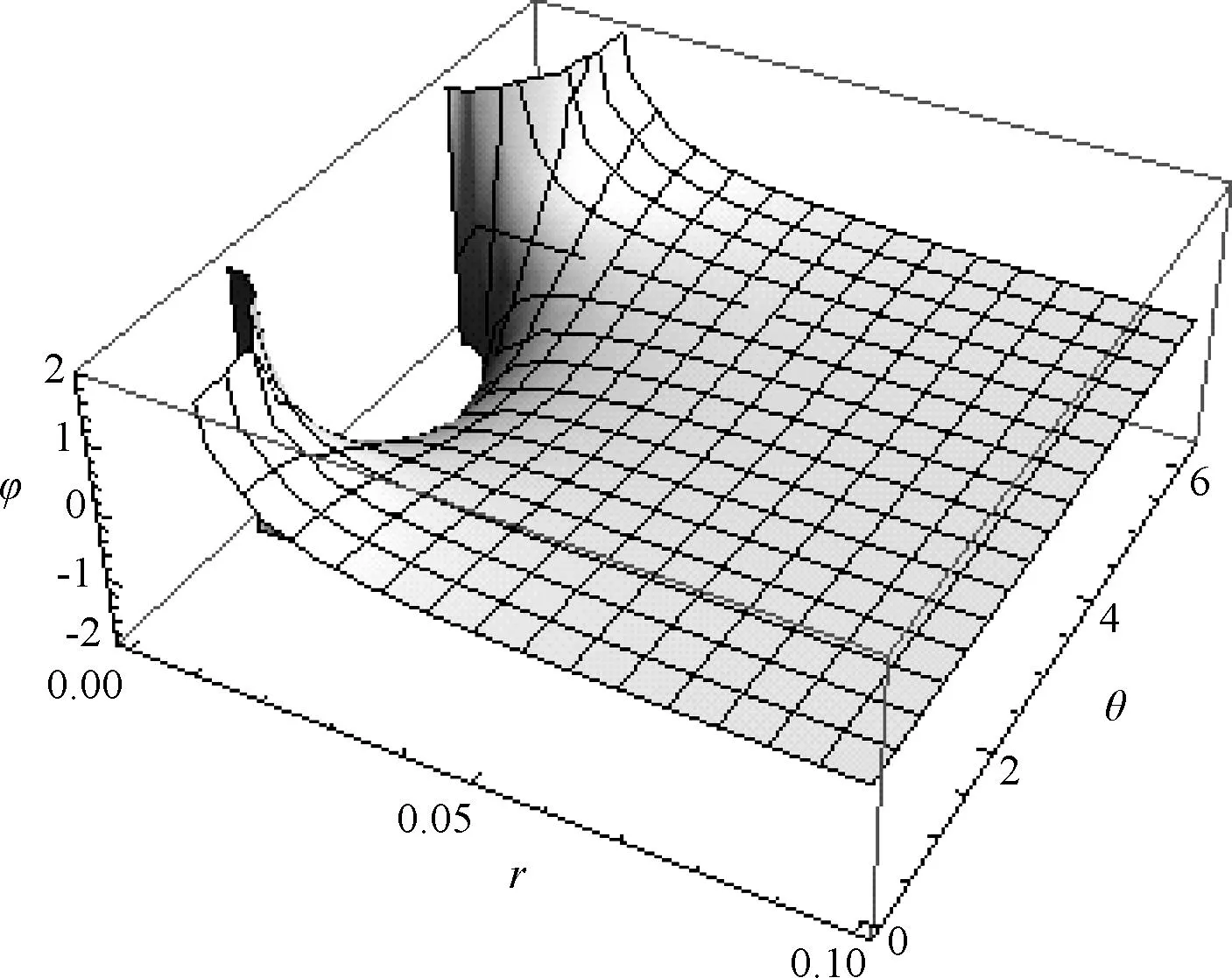
分析:如圖1所示,由于球體具有球對稱性,因此在三維空間我們可以選取球坐標(r、θ、φ)來研究電場強度.在r>R的空間,可以將球體看成點電荷模型處理.在r 解:(1) 通過以上分析可得到的結論是:任一同心球面上場強大小E都相等,方向與此球面垂直.接下來需要利用靜電場的高斯定理來計算場強的大小. 圖2 圖2給出了該種帶電球體電場強度的函數分布圖.可以看出,均勻帶電體的場強是連續的,且在球體表面處場強有極大值. 圖2也給出了該種帶電體電勢的函數分布圖,不難看出,均勻帶電球體周圍的電勢和電場一樣也是連續的,且電勢在球心處有最大值. 這里要說明兩點:其一,由于均勻帶電體不是一個穩定狀態,電荷最終會向帶電體表面移動,形成一個帶電面,尤其是導體,此時場強或電勢分布將會出現變化(本文第2部分將會說明).其二,若是針對均勻帶電體,按照高斯定理,體內的場強就不會是零,這點很容易與處于靜電平衡的帶電體內場強為零的結論相混淆. 2均勻帶電球殼的場強及電勢分布 問題:均勻帶正電球殼置于真空中,帶電量為Q,球殼半徑為R,球心為O,求球殼周圍空間的電場強度及電勢. 分析:如圖3所示,帶電體為球殼,相比帶電球體,其選用的坐標系和理論方法同出一轍,但場強的計算要簡單得多.在處理這個問題時,同樣分r>R和r 圖3 若P點在球內(圖3中高斯面S2),此時發現,任一高斯面內均沒有電荷,故在球殼內部任一點的場強E=0. (2) 選擇無窮遠點為電勢的參考位置. 對比帶電球體和球殼,不難看出,各自的場強和電勢分布有很大不一樣.首先,對于場強而言,前者是連續的,極大值出現在球體表面處,而后者則是跳躍的,且球殼內部場強處處為零,類似靜電平衡的導體;其次,對電勢而言,前者電勢一直在降低,后者在球殼內部的電勢不變,為一等勢體. 3等量異種電荷的場強及電勢分布 圖4 圖4給出了真空中等量異種電荷模型,兩電荷各自帶電量為q,相距l,O為電荷連線中點.求與電荷模型距離較遠的P點的電勢和場強分布. 圖5 圖6 4場強及電勢分布一般處理方法 通過以上計算及相關模擬,在求解帶電體的電勢或場強時,二者是等價的.如果帶電體的場強相對說來比較好求解,可以先求解場強,進而求解電勢,而這種帶電體多為單個帶電體,且幾何形狀比較規則;假若帶電體為多個,一般是先求解電勢,之后求解場強,因為電勢的求解就是普通的標量疊加,相比場強的矢量疊加來說較為簡單. 參考文獻: [1] 趙凱華,陳熙謀.電磁學 [M]. 北京:高等教育出版社,2006 :20-24. [2] 中學物理教師手冊編寫組.中學物理教師手冊(下冊)[M]. 上海:上海教育出版社,1983 :470-472.