一種多傳感器的盲區邊緣定位精度改進的算法

左曉敏，李金厚，劉輝，張學峰

（安徽工業大學計算機科學與技術學院，安徽馬鞍山243002）

一種多傳感器的盲區邊緣定位精度改進的算法

左曉敏，李金厚，劉輝，張學峰

（安徽工業大學計算機科學與技術學院，安徽馬鞍山243002）

針對多傳感器觀測盲區兩側邊緣處出現誤差較大現象，提出基于閾值的盲區兩側附近異常數據的檢測方法。對原有數據沿x軸、y軸方向進行正交分解，分別選取檢測這兩個方向分量上異常數據的閾值。在此基礎上，對原有數據進行篩選，然后通過適當的填補方法，依次對這兩個方向上剔除掉的數據進行填補，獲得完整的數據集，以替代原有數據。仿真結果表明，采用新算法可以明顯提高目標在盲區邊緣附近的定位精度。

異常數據；檢測；傳感器；定位

在跟蹤定位系統中，多傳感器的數據融合，是對多傳感器的原始信息利用信息融合技術進行處理，以達到實現高性能的跟蹤定位效果。但由于傳感器的系統偏差和隨機誤差的存在，在目標跟蹤系統中，目標的定位計算受到很大的影響。其中，現有的濾波方法可以消除隨機誤差，而系統誤差，因為具有確定性，所以濾波方法無法將其去除[1]。需要事先對系統誤差進行估計，再對后續的傳感器配準進行補償，這一過程稱為誤差配準[2]。傳感器數據融合技術的發展離不開傳感誤差配準技術的發展，后者為前者提供技術保障。現如今這種技術已成為傳感器配準研究中的熱點問題，同時也是難點問題[3-4]。

在解決傳感器固定偏差情況下的配準，Okello.N和Ristic.B在Maximum likelihood registration for multiple dissimilar sensors中提出—種離線的極大似然配準算法[5]，這種算法與傳統偏差估計方法（如最小二乘法和極大似然估計法）相比，優勢在于不強調傳感器需要配對組合之后使用。不足在于要求明確傳感器時鐘完全同步，并且知道傳感器的精確位置[6]。

祁永慶提出基于信息融合的修正極大似然配準算法[7]。采用了冗余信息補償方法處理被動傳感器在觀測盲區內目標不可觀測的問題。但由于具有不同配準偏差的傳感器存在，在數據采集過程中容易產生粗大誤差，導致在傳感器觀測盲區兩側的邊緣處，定位軌跡上會顯現少許的間隔或重疊誤差較大情況。

在定位盲區兩側邊緣處目標跟蹤航跡出現的間隔和重疊等偏差較大的問題，將粗大誤差較大的數據視為異常數據。在檢測異常數據研究上，許多學者做出了重大的貢獻，發現了許多有效的算法。學者樂立利針對雙參數對數正態分布下情況提出相應的異常數據檢測算法[8]。肖瑛[9]首次將3σ準則應用到檢測異常數據方面。盡管前人在異常數據檢測算法上取得很大的研究成果，但應用改善多傳感器觀測盲區邊緣處定位效果上效果不佳。

1 基本誤差配準數據的獲取

根據祁永慶在文獻[6]第三章中關于基于信息融合的修正極大似然配準算法及其仿真模型，獲取定位結果如圖1所示。

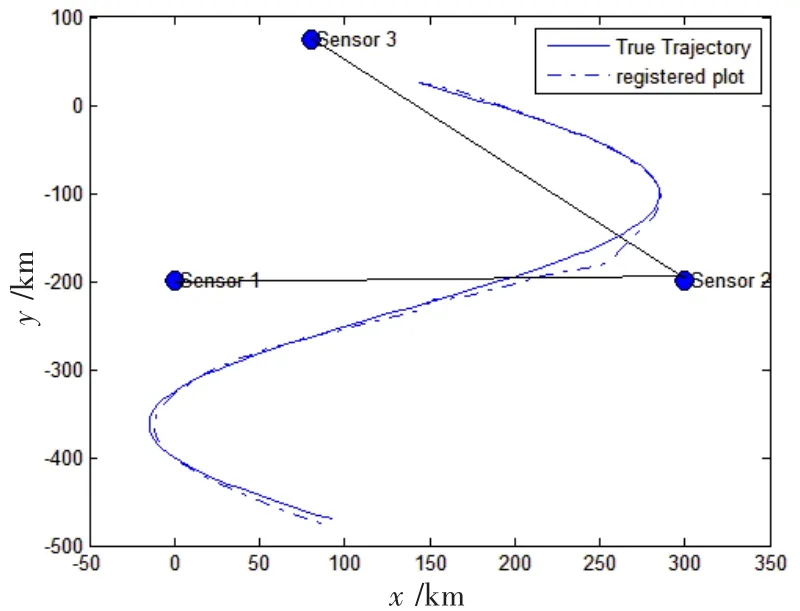
圖1 目標定位軌跡與真實軌跡對比

在圖1目標定位軌跡圖中，可以看出修正極大似然配準算法對目標狀態的定位已經很逼近，但在其中兩傳感器之間的連線（盲區）附近，目標的定位出現誤差較大現象，也就是在其論文第三章仿真分析中提到的盲區邊緣處仍然存在少許間斷和重疊情況[7]。為此，文中將對兩兩傳感器附近的數據做進一步處理，以達到定位誤差的再次降低。

2 異常數據的處理方法

2.1 異常數據的檢測

由第1節中得到的的誤差配準數據，作為待處理的初始數據，記為：。

針對正弦曲線和直線這類曲線，可知在這連續曲線上的點，同一固定的點（如觀測站）間的距離的差值，這種差值之間的波動大小會保持平緩地變化。如果出現較周圍附近的點變化幅度較大情況，則將其視為異常數據。然而針對目標的軌跡曲線是其他類型曲線時，原理是相同。

文中以此為依據，提出檢測異常數據閾值的一種方法。圖2為x方向分量檢測異常數據示意圖，觀測站S對目標在k時刻的位置Ak的測量距離為，觀測站S對目標在k+1時刻的位置Ak+1的測量距離為，其中，k=1，…，N-1；前后兩個時刻的距離差值，其中，k1=2，…，N；距離差值的波動大小，其中，k2=3，…，N；如果滿足條件，則Ak+1點可判斷為含誤差的數據，應予剔除，所以，把作為新的判別異常數據的判據。

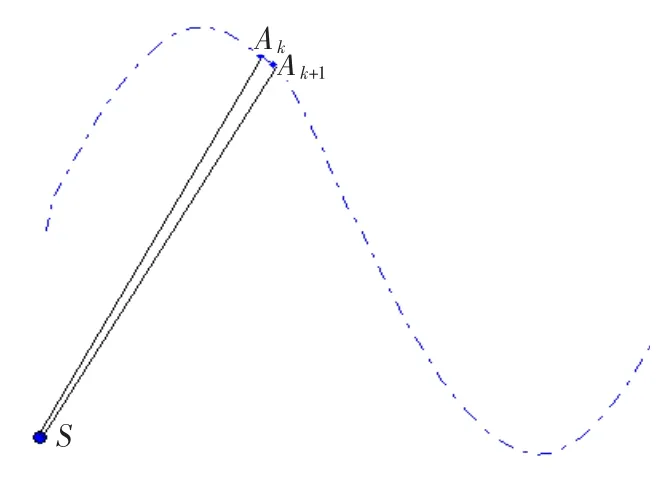
圖2 異常數據檢測示意圖

基于該方法的剔除步驟如下：

（1）選取一個觀測站S（ξ1，η1），令其x方向位置為固定點S（ξ1，0）；

（2）計算測量距離差值的波動值

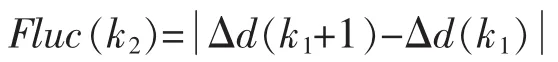
（3）選取門檻值εx，大量仿真試驗，調試選取使定位精度最高的門檻值；

（5）同理，可以得到y方向分量。

2.2 門檻值選取

x，y方向上，目標軌跡曲線上不同時刻的點與固定的觀測站間的距離的差值，這種差值之間的波動大小如圖3。

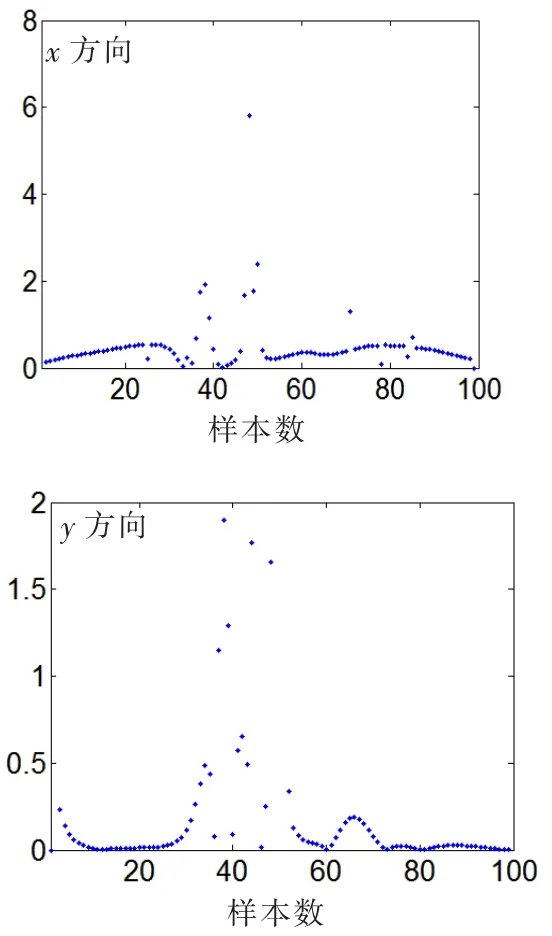
圖3 前后兩點間距離的差值圖

在圖3中，根據波動大小數值來選取用于篩選異常數據的門檻值。

門檻值εx，εy在取不同的值的情況下，將含有配準誤差的數據進行篩選，針對剔除后剩下的數據，運用現有的代數多項式擬合方法，獲取完整的數據集[10]。

圖4（a），（b）所示，在不同的數據集的情況下，x，y兩個方向上數據的均方根誤差值（RMSE）變化很大，這表明了門檻值選取對獲取具有最小均方根誤差值的數據集具有直接作用，同時對縮小目標在盲區邊緣處的定位誤差，也將具有良好的效果。

在圖4中，比較兩個方向分量上的均方根誤差值（RMSE），選取最低均方根誤差值，以及相應的篩選這些數據的門檻值參數。其中門檻值參數用于后續的仿真計算。

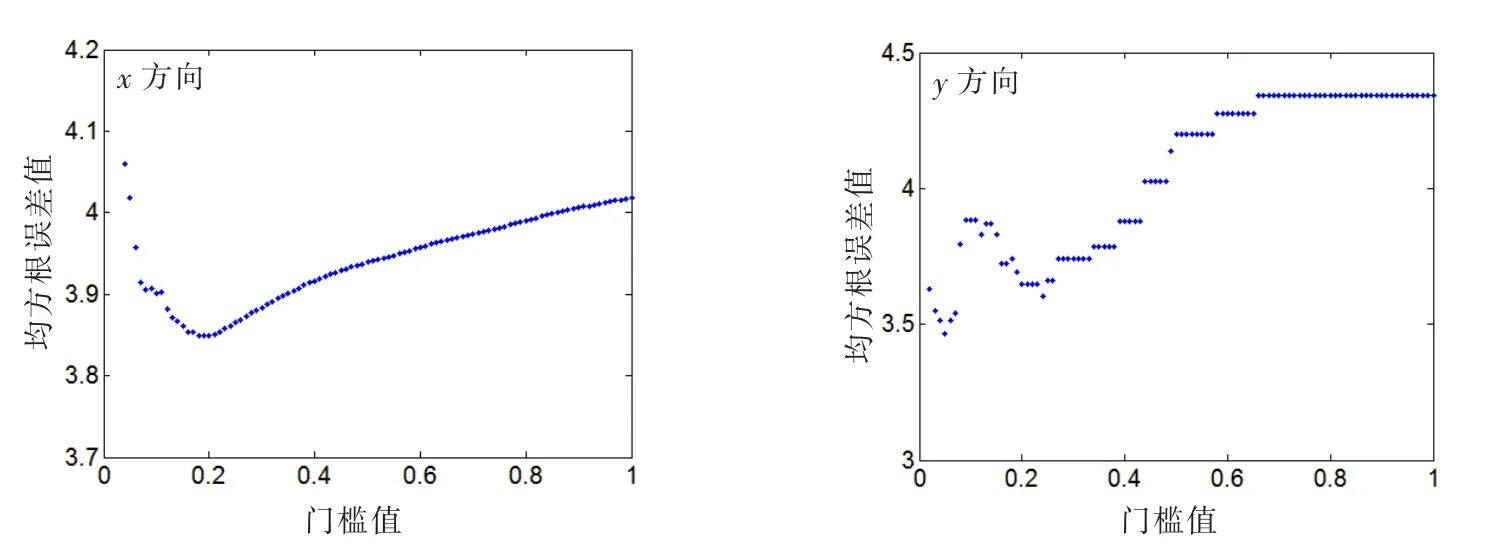
圖4 不同門檻值下的RMSE值

3 算法流程圖（如圖5）

以x方向上分量處理方法為例，針對估計出的含有誤差的配準數據，將其作為待處理的數據，在此基礎上采用文中的異常數據檢測方法，對配準后的數據進行處理，進而更新目標的定位信息。

同理，可更新y方向上分量的狀態信息。與修正的極大似然配準算法的區別在于：筆者需要從其x，y兩個方向上分量判別配準后的目標軌跡前一時刻與后一時刻同觀測站的距離差值的波動大小，決定是否剔除。如果剔除，將通過對篩選出符合條件的數據集進行多項式擬合，實現了將缺失的數據填補完整，最終重新確定完備數據，更新目標狀態信息。

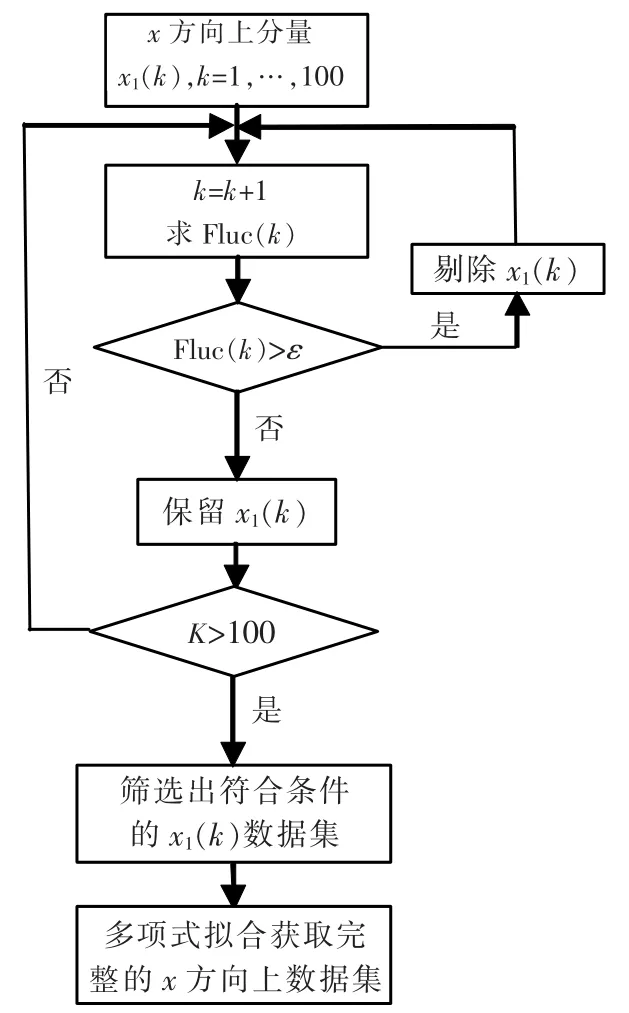
圖5 新算法流程圖（x方向分量為例）

4 仿真計算結果及分析

考慮由3個被動傳感器構成的多平臺系統，假定傳感器是同步的，傳感器的坐標是固定的且是已知的。若僅考慮二維平面，則被動傳感器都是一維的，僅測量目標的方位角。目標的真實航跡的狀態方程為[3]：x1（k）=135+150sin（0.06k），y1（k）=30-5k。其中，k=1，…，N，（N=100）。傳感器的坐標分別為S1=（0，-200），S2=（300，-200），S3=（80，-75），單位為km。偏差分別為Δθ1= -7.0°，Δθ2=7.0°，Δθ3=-4.0°。測量噪聲的標準方差分別為°

4.1 定位結果比較

新方法得到的目標軌跡與修正極大似然配準算法（modified MLR）的相應軌跡對比如圖6所示。其中，“-.-”點畫線為真實目標軌跡曲線；“--”長虛線表示修正極大似然配準算法的軌跡曲線；實線表示為新方法定位軌跡曲線。

由圖6不難看出，當目標接近傳感器觀測盲區時，其附近的邊緣處出現的間隔現象也明顯減少，這一仿真結果充分驗證了新方法的定位軌跡更逼近真實軌跡。

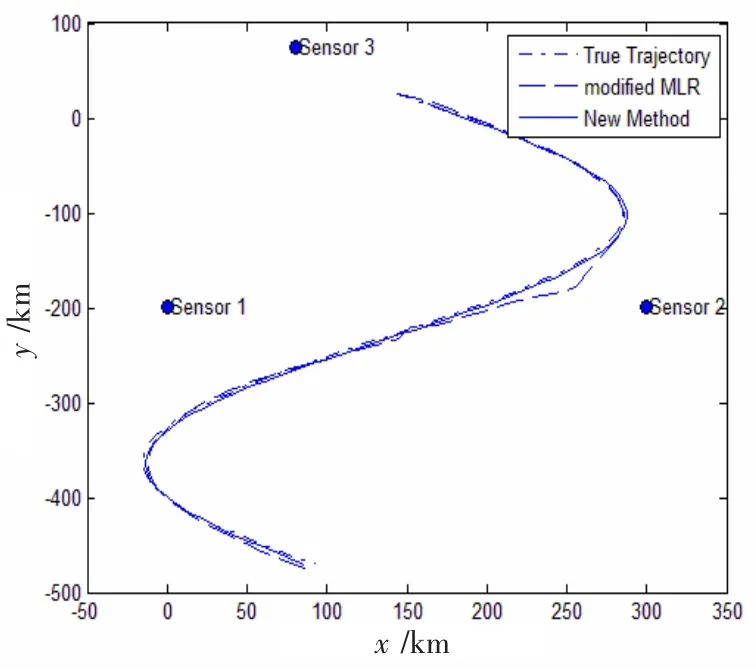
圖6 兩種方法完整定位軌跡比較

4.2 定位誤差比較

新方法處理后的目標的完整的定位數據誤差情況如圖7所示。其中“-.-”點畫線表示新方法定位誤差；實線表示修正極大似然配準算法的定位誤差。

由圖7可知，隨著采樣次數的增加，新方法比祁的修正極大似然配準算法的定位精度更高，尤其是在采樣時刻30-50之間，也就是傳感器的觀測盲區附近，誤差降低更加明顯。因而，筆者提出的采用新判據剔除了含誤差配準數據中的異常數據的方法，有效地提高了傳感器觀測盲區兩側的邊緣處的定位精度。

5 結語

文中提高配準精度的新改進算法是針對盲區兩側邊緣處目標跟蹤航跡重疊和間隔的問題提出的，其核心思想是利用目標軌跡前一時刻與后一時刻同觀測的距離差值的波動情況，將篩選出的異常數據剔除，然后通過適當的回歸填補法，對兩個方向上的數據進行更新，重新獲得傳感器的目標狀態。仿真結果表明，新算法提高了傳感器觀測盲區兩側邊緣處的定位精度。

[1]張志云，周永豐.基于最小二乘和廣義最小二乘的系統偏差估計研究[J].艦船電子工程，2008，28（8）：89-91.

[2]何友，修建娟，張晶煒，等.雷達數據處理及應用[M].2版.北京：電子工業出版社，2009.

[3]何友，王國宏.關欣信息融合理論及應用[M].北京：電子工業出版社，2010.

[4]宋強，何友，熊偉.基于極大似然的單傳感器誤差配準算法[J].宇航學報，2011，32（8）：1824-1833.

[5]Okello N，Ristic B.Maximum likelihood registration for multiple dissimilar sensors[J].IEEE Transactions on Aerospace and Electronic systems，2003，39（3）：1074-1083.

[6]祁永慶.多平臺多傳感器配準算法研究[D].上海：上海交通大學，2008.

[7]祁永慶，敬忠良，胡士強.基于信息融合的修正極大似然配準方法[J].中國光學快報，2007，5（11）：639-641.

[8]樂立利，曾海群.雙參數對數正態分布異常數據的檢測方法[J].數學理論與應用，2009，29（1）：29-32.

[9]肖瑛，董玉華.基于小波網絡的遙測視速度異常數據剔除方法[J].大連民族學院學報，2009,11（3）：215-218，281.

[10]侯賀.缺失數據處理方法的研究及其在軟測量技術中的應用[D].沈陽：東北大學，2011.

An improved multi-sensor algorithm for higher position-accuracy near the blind spots

ZUO Xiaomin，LI Jinhou，LIU Hui，ZHANG Xuefeng
（School of Computer Science&Technology，Anhui University of Technology，Ma'anshan 243002，China）

Aiming at the phenomenon that the error becomes larger when the target occurs on either side of the blind spots of the multi-sensor，we have proposed a method detecting the outlier near either side of the blind spots based on the threshold.Along the x axis and y axis，the original data was divided into two groups based on orthogonal decomposition.Then two thresholds were selected to detect the outliers separately.On the basis of this analysis，the original data was discriminated.And then the proper imputation methods were selected to deal with the missing data and get the complete data set.The original data were replaced with the new complete data.Simulation results show that the accuracy of the target positioning near the blind spots can be obviously improved by using this proposed algorithm.

outlier；detection；sensor；position

TP274；TN957

A

1672－0687（2015）02－0065－04

責任編輯：艾淑艷

2014－07－08

安徽省自然科學基金資助項目（1308085QF113）

左曉敏（1989-），女，江蘇連云港人，碩士研究生，研究方向：傳感器定位，異常數據檢測。