PCB板動(dòng)態(tài)分析等效建模方法

楊 強(qiáng)，杜平安，周 元，游 冬，王 勇

(1. 電子科技大學(xué)機(jī)械電子工程學(xué)院 成都 611731; 2. 中國(guó)電子科技集團(tuán)第24研究所 重慶 南岸區(qū) 400060;3. 西南電子技術(shù)研究所 成都 610036)

PCB板是電子設(shè)備的核心部件，由印制板(基板)和安裝在板上的各類元器件構(gòu)成。由于元器件數(shù)量多、形狀復(fù)雜、大小不一，在利用有限元法進(jìn)行PCB板的動(dòng)態(tài)特性分析時(shí)，會(huì)導(dǎo)致分網(wǎng)過(guò)程復(fù)雜，網(wǎng)格和節(jié)點(diǎn)數(shù)量巨大。特別是在進(jìn)行設(shè)備整機(jī)(系統(tǒng)級(jí))動(dòng)態(tài)特性分析時(shí)，要詳細(xì)考慮各類元器件進(jìn)行詳細(xì)建模幾乎不可能。因此需要對(duì)PCB板進(jìn)行等效建模，即忽略(或部分忽略)板上元器件，以使分網(wǎng)過(guò)程能夠進(jìn)行，且模型規(guī)模得到控制[1-4]。

國(guó)內(nèi)外學(xué)者圍繞PCB板的等效建模做了大量的研究。文獻(xiàn)[5]提出利用區(qū)域等效來(lái)建立PCB板的有限元模型，但當(dāng)板上元器件數(shù)目眾多且分布不均時(shí)，劃分區(qū)域太多，導(dǎo)致分網(wǎng)過(guò)程復(fù)雜。文獻(xiàn)[6]研究了PCB板的5種等效建模方法，其中4種方法都不同程度忽略了元器件質(zhì)量與剛度的影響；文獻(xiàn)[7]將PCB板上小元器件質(zhì)量均布在基板上，大元器件簡(jiǎn)化為集中質(zhì)量點(diǎn)；文獻(xiàn)[8]提出了PCB板在動(dòng)態(tài)分析時(shí)，其等效模型等效剛度的一種計(jì)算方法，但未給出具體的適用范圍。

鑒于目前各類等效方法的局限，本文根據(jù)工程應(yīng)用需求，提出一種基于等效楊氏模量的等效建模方法。該方法以等效前后PCB板的固有頻率相等為原則，將實(shí)際PCB板等效為均質(zhì)、等厚的光板。利用單位楊氏模量模型，推導(dǎo)出第i階等效模型的楊氏模量。基于最小二乘法，求得多階頻率下等效楊氏模量表達(dá)式。把等效楊氏模量和密度賦予等效模型，將使整機(jī)分析分網(wǎng)過(guò)程大大簡(jiǎn)化，網(wǎng)格數(shù)量大幅度減少，同時(shí)能有效地保證等效前后固有頻率不變。

1 PCB板等效建模方法

1.1 等效建模基本思路

工程上常見(jiàn)的PCB板如圖1a所示，包含基板及安裝在基板上的電阻、電容、功能芯片、插槽和接口等部件，由于插槽剛度較低，電阻、電容等元件尺寸較小，在設(shè)備系統(tǒng)級(jí)動(dòng)態(tài)分析時(shí)可忽略它們的局部動(dòng)態(tài)性能，可將原PCB板等效為如圖1b所示的均勻密度的等厚板，并將等效后的PCB板用于電子設(shè)備整機(jī)的動(dòng)態(tài)分析。

圖1 PCB板結(jié)構(gòu)模型圖

PCB板的等效原則是保證等效前后固有頻率不變。實(shí)現(xiàn)方法為：1) 保持等效模型的長(zhǎng)寬尺寸和厚度與等效前的基板相同；2) 等效模型材料的泊松比與基板相同，并將元器件質(zhì)量均勻分布在等效板上，即保持等效模型為均質(zhì)、等厚的薄板；3) 通過(guò)改變等效模型的材料楊氏模量來(lái)保證等效前后固有頻率相同。因此可建立等效關(guān)系為：

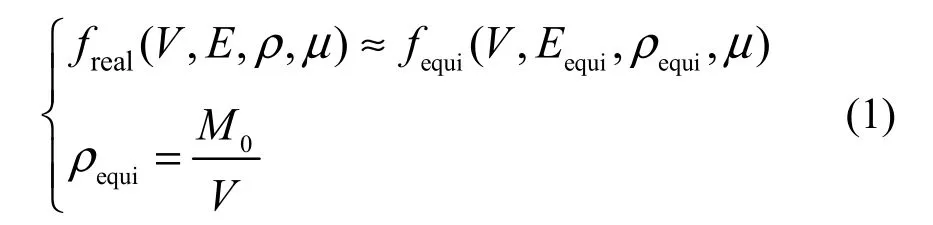
式中，f 為固有頻率；V為幾何尺寸；E為楊氏模量；ρ為密度；μ為泊松比；M0為原PCB板質(zhì)量；下標(biāo)real和equi分別表示原模型和等效模型。

從式(1)可以看出，等效后僅有Eequi為未知，即等效模型的彈性模量，稱為等效楊氏模量。

1.2 等效楊氏模量推導(dǎo)

根據(jù)振動(dòng)理論[9]，結(jié)構(gòu)自由振動(dòng)特征方程為：

式中，K為剛度矩陣；M為質(zhì)量矩陣；ω為固有頻率。由式(2)得到原PCB板第i階模態(tài)方程為：

式中，iω為原來(lái)PCB板第i階固有頻率；ui為第i階振型。

為求得等效楊氏模量，首先建立單位楊氏模量模型，即滿足等效原則式(1)和式(2)，且E=1的模型。根據(jù)式(3)可求得單位楊氏模量模型的模態(tài)方程為：

式中，Kus為單位楊氏模量模型的剛度矩陣；Mus為質(zhì)量矩陣；下標(biāo)us表示單位楊氏模量模型。

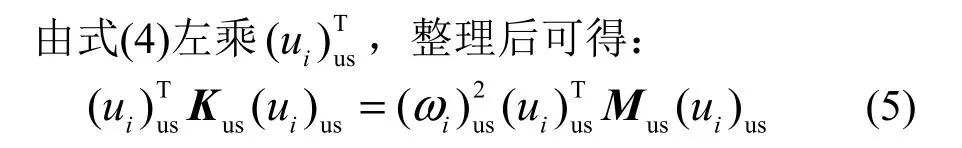
根據(jù)有限元理論[10]，對(duì)于均勻等厚板，剛度矩陣和單位楊氏模量剛度矩陣成正比，即有：

由等效原則式(2)可知，等效模型質(zhì)量矩陣與單位楊氏模量質(zhì)量矩陣相等，即有：

根據(jù)振動(dòng)理論[11]，單位楊氏模量模型的振型(ui)us和PCB板等效模型的振型(ui)equi相同。由于模態(tài)階數(shù)不同，等效楊氏模量不同，用(Ei)equi表示第i階模態(tài)的等效楊氏模量，因此等效模型的模態(tài)方程可表示為:

式(10)等號(hào)右邊的所有參數(shù)為已知，因此可利用該式求解等效模型第i階模態(tài)的楊氏模量。工程上一般關(guān)心結(jié)構(gòu)的低階頻率，特別是基頻，所以通過(guò)式(10)求得的PCB板第一階模態(tài)等效楊氏模量已能滿足工程應(yīng)用需求。

1.3 多階頻率下等效楊氏模量推導(dǎo)

當(dāng)同時(shí)考慮多階頻率下的等效楊氏模量時(shí)，式(10)不再適用。為減小等效模型與實(shí)際模型固有頻率的相對(duì)誤差，利用最小二乘法，建立前n階頻率相對(duì)誤差為：

式中，y為頻率的相對(duì)誤差，實(shí)際上是等效模型第i階頻率等效楊氏模量與考慮多階頻率時(shí)的等效楊氏模量之間的相對(duì)誤差，所以式(11)中頻率參數(shù)可由楊氏模量參數(shù)代替得到：

式中，Eequi為考慮多階頻率的楊氏模量。

為了使 y*的值最小，需滿足：

由式(14)可知，多階頻率下等效楊氏模量是由每階模態(tài)的等效楊氏模量共同決定的，該求解方法是一種均勻化方法。

當(dāng)n=1時(shí)，式(14)可化簡(jiǎn)為：

式(15)與式(11)相同，表明多階頻率下的等效楊氏模量對(duì)單階頻率等效也同樣適用。

從PCB板的等效建模方法可看出，當(dāng)PCB板上元器件越小，分布越均勻，等效前后頻率誤差越小，等效效果越好。

2 元器件對(duì)等效楊氏模量的影響分析

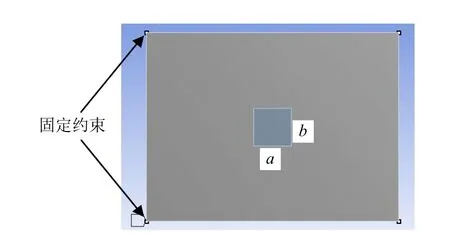
圖2 PCB板結(jié)構(gòu)模型示意圖

元器件與PCB之間的接觸面積、元器件高度對(duì)等效楊氏模量都有一定影響，本文以圖2所示算例進(jìn)行說(shuō)明。設(shè)PCB板尺寸0.2 m×0.15 m×0.002 m，材料楊氏模量22 GPa，泊松比0.28，密度1 850 kg/m3。元器件位于板中央，楊氏模量26.5 GPa，泊松比為0.42，密度4 600 kg/m3。板的4個(gè)角點(diǎn)固定。等效模型尺寸為0.2 m×0.15 m×0.002 m，泊松比0.28。

2.1 接觸面積對(duì)等效楊氏模量的影響

元器件與PCB間的接觸面積不同，結(jié)構(gòu)的剛度和質(zhì)量分布不同，從而影響等效楊氏模量。對(duì)于圖2所示模型，利用單階頻率等效法，分別取不同的接觸面積S(S=a×b，見(jiàn)圖2)，等效楊氏模量Eequi與S的關(guān)系如圖3所示。

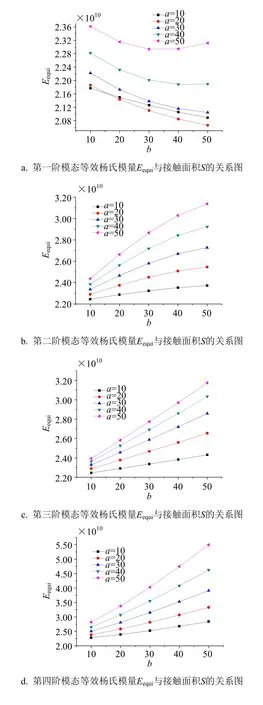
圖3 等效楊氏模量E equi與接觸面積S的關(guān)系圖

從圖3可看出：1) 對(duì)于第一階模態(tài)，當(dāng)a一定時(shí)，隨著b增加，等效楊氏模量的變化規(guī)律不同；當(dāng)b一定時(shí)，隨著a增加，等效楊氏模量總體呈上升趨勢(shì)，這主要是由于板結(jié)構(gòu)一階模態(tài)振幅的最大位置位于板中央，導(dǎo)致元器件所在位置是振動(dòng)薄弱位置，且元器件的長(zhǎng)邊方向與PCB長(zhǎng)邊方向一致時(shí)，頻率越高，導(dǎo)致等效楊氏模量越高；2) 對(duì)于第二到第五階模態(tài)，當(dāng)a一定時(shí)，隨著b增加，等效楊氏模量上升；當(dāng)b一定時(shí)，隨著a增加，等效楊氏模量也上升。這主要是由于a或b的增加，增大了元器件與板間的接觸面積S，相當(dāng)于增加了它們間的接觸剛度，導(dǎo)致整體結(jié)構(gòu)剛度增加；3) 各階模態(tài)等效楊氏模量的變化規(guī)律不同，說(shuō)明接觸面積S對(duì)每階模態(tài)等效楊氏模量影響不同。

利用一階等效楊氏模量作為等效模型的楊氏模量，等效模型頻率相對(duì)誤差δ與接觸面積S的關(guān)系如圖4所示。

圖4 等效頻率相對(duì)誤差δ與接觸面積S的關(guān)系

從圖4可以看出：1) 一階模態(tài)頻率相對(duì)誤差接近于0，說(shuō)明等效結(jié)構(gòu)和原結(jié)構(gòu)的一階頻率非常吻合。由于工程中常常關(guān)心結(jié)構(gòu)的一階模態(tài)，因此可滿足大多數(shù)工程需要。2) 一階頻率等效時(shí)，其他每階頻率的誤差變化規(guī)律不同，說(shuō)明結(jié)構(gòu)模型每階頻率對(duì)接觸面積S變化引起的剛度和質(zhì)量的分布的靈敏度不同，當(dāng)接觸面積S較大時(shí)，第二到第五階頻率誤差很大，且隨著接觸面積S的變化而變化，說(shuō)明元器件接觸面積越小，頻率相對(duì)誤差越小，等效效果越好。

2.2 元器件高度對(duì)等效楊氏模量的影響

利用單階頻率等效方法，分別取不同的元器件高度，計(jì)算得到等效楊氏模量Eequi與元器件高度h的關(guān)系如圖5所示。

從圖5可看出，隨著元器件質(zhì)心遠(yuǎn)離PCB板，等效楊氏模量變化較復(fù)雜，一階頻率等效剛度以類似直線下降變化，第二到第五階頻率等效剛度總體呈上升趨勢(shì)。采用一階頻率等效的等效剛度，等效模型的頻率相對(duì)誤差δ如圖6所示。

從圖6可以看出，1) 單階頻率等效時(shí)，一階頻率相對(duì)誤差非常小；2) 第二到第五階頻率相對(duì)誤差，隨著高度h的增加而呈現(xiàn)上升趨勢(shì)，說(shuō)明元器件高度越低，等效效果越好。

圖5 等效楊氏模量E equi與元器件高度h的關(guān)系圖

圖6 等效頻率相對(duì)誤差δ與元器件件高度h的關(guān)系圖

3 實(shí)例分析

本文利用ANSYS軟件對(duì)某電源模塊PCB板進(jìn)行動(dòng)態(tài)分析，以驗(yàn)證等效建模方法的有效性。PCB板模型及等效模型如圖7所示。PCB板楊氏模量為22 GPa，泊松比為0.28，密度為1 850 kg/m3。原PCB板采用大小為0.001 2 m的20節(jié)點(diǎn)186單元和10節(jié)點(diǎn)187單元，共217 124個(gè)節(jié)點(diǎn)和125 590個(gè)單元。等效板采用大小為0.001 2 m的10節(jié)點(diǎn)187單元，共167 536個(gè)節(jié)點(diǎn)和84 783個(gè)單元。可見(jiàn)，等效后PCB板有限元模型的規(guī)模大大減小，而且劃分網(wǎng)格非常容易。

圖7 電源模塊PCB板幾何模型及等效模型圖

根據(jù)工程需要，考慮前二階頻率等效。計(jì)算得到等效楊氏模量42.152 GPa，密度3 237.6 kg/m3。等效模型的各階頻率誤差如表1所示。

表1 等效模型頻率相對(duì)誤差表

由表1可以看出，等效模型的前兩階模態(tài)頻率和原PCB模型頻率相對(duì)誤差在5%以內(nèi)，能滿足工程應(yīng)用精度要求；兩階頻率相對(duì)誤差相差很接近，說(shuō)明多階頻率等效方法是一種均勻化方法，與理論推導(dǎo)一致。

用等效模型代替原PCB板進(jìn)行電源整機(jī)建模，整機(jī)模型及有限元模型如圖8所示。與原來(lái)模型相比，等效后模型節(jié)點(diǎn)數(shù)量減少49 588個(gè)，單元數(shù)量減少40 807個(gè)。

圖8 電源模塊整機(jī)模型及其等效后模型圖

前兩階頻率及相對(duì)誤差δ如表2所示。

表2 采用等效PCB板的電源頻率及其相對(duì)誤差表

從圖8和表2可以看出，采用等效模型后的有限元模型更簡(jiǎn)單，劃分網(wǎng)格更容易，分析時(shí)間更短，且頻率的相對(duì)誤差均小于3%，既能滿足工程應(yīng)用需要，又說(shuō)明了該等效方法的有效性。

4 結(jié) 束 語(yǔ)

基于單位楊氏模量模型，對(duì)于帶有多種小元器件的PCB板，本文提出一種PCB板動(dòng)態(tài)分析等效建模方法。該方法先將原PCB板簡(jiǎn)化為等厚度的板，由質(zhì)量相等原則得到等效密度，并且對(duì)單階頻率等效楊氏模量進(jìn)行了推導(dǎo)，然后基于最小二乘法，求得了多階頻率下等效楊氏模量的表達(dá)式。分析了元器件與PCB間接觸面積和元器件高度對(duì)等效楊氏模量的影響。應(yīng)用實(shí)例表明，采用本文的PCB板等效建模方法，能大大簡(jiǎn)化有限元模型，同時(shí)能有效地保證工程上要求的計(jì)算精度，因此對(duì)于儀器儀表的系統(tǒng)級(jí)分析具有很高的實(shí)際應(yīng)用價(jià)值。

[1] 李曉明, 呂善偉, 高澤溪, 等. PCB及元件的溫度場(chǎng)有限元分析[J]. 北京航空航天大學(xué)學(xué)報(bào), 2000, 26(1): 5-7.LI Xiao-m ing, Lü Shan-wei, GAO Zhe-xi, et al. Finiteelement analysis of temperature field of PCB and components[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(1): 5-7.

[2] 趙健. PCB組件熱-力分析的有限元模型及仿真[D]. 天津:天津大學(xué), 2006.

ZHAO Jian. The finite element modeling and simulation for thermomechanical analysis of PCBA[D]. Tianjin: Tianjin University, 2006.

[3] 杜平安, 劉建濤, 劉孝保. 電子器件振動(dòng)特性有限元模型參數(shù)的等效計(jì)算[J]. 電子學(xué)報(bào), 2010, 38(8): 1867-1873.

DU Ping-an, LIU Jian-tao, LIU Xiao-bao. Equivalent computational methods of finite element model’s parameters for vibration analysis of electronic module[J]. Acta Electronica Sinica, 2010, 38(8): 1867-1873.

[4] AMY R A, AGLIETTI G S, RICHARDSON B G.Sensitivity analysis of simplified PCB finite element models[J]. M icroelectronics Reliability, 2009, 49(7): 791-799.

[5] PITARRESI J M, CALETKA D V, CALDWELL R. The“smeared” property technique for the FE vibration analysis of printed circuit cards[J]. ASME Journal of Electronic Packaging, 1991, 113: 250-257.

[6] PITARRESI J M, PRIMAVERA A A. Comparison of modeling techniques for the vibration analysis of printed circuit cards[J]. ASME Journal of Electronic Packaging,1992, 114(4): 378-383.

[7] 李春洋, 陳循, 陶俊勇, 等. 基于模態(tài)分析的印制電路板振動(dòng)可靠性研究[J]. 中北大學(xué)學(xué)報(bào)(自然科學(xué)版), 2007,28(2): 156-160.

LI Chun-yang, CHEN Xun, TAO Jun-yong, et al. Study on printed circuit board reliability under vibration stress based on modal analysis[J]. Journal of North University of China(Natural Science Edition), 2007, 28(2): 156-160.

[8] 劉孝保, 杜平安, 夏漢良, 等. 一種面向動(dòng)態(tài)分析的PCB板等效建模方法[J]. 儀器儀表學(xué)報(bào), 2011, 32(4): 863-869.

LIU Xiao-bao, DU Ping-an, XIA Han-liang, et al. Dynamic property analysis-oriented PCB equivalent modeling method[J]. Chinese Journal of Scientific Instrument, 2011,32(4): 863-869.

[9] 倪振華. 振動(dòng)力學(xué)[M]. 西安: 西安交通大學(xué)出版社,1989.

NI Zhen-hua. Vibration mechanics[M]. Xi’an: Xi’an Jiaotong University Press, 1989.

[10] RAMTEKKAR G S, DESAI Y M, SHAH A H. Natural vibrations of laminated composite beams by using mixed finite element modeling[J]. Journal of Sound and Vibration,2002, 257(4): 635-651.

[11] VEL S S, BATRA R C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates[J]. Journal of Sound and Vibration, 2004, 272(3-5):703-730.

編 輯 黃 莘