BDS／GPS系統時差的組合實時預報模型分析

付文舉 張 勤 黃觀文

1 長安大學地質工程與測繪學院，西安市雁塔路126號，710054

兼容性是北斗衛星導航系統（BDS）的4大建設原則之一，其目標是實現與世界各衛星導航系統的兼容與互操作［1］。系統時差作為兼容與互操作的重要組成部分，對其進行監測和預報具有重要意義。BDS／GPS系統時差是指BDS系統時間（BDT）與GPS系統時間（GPST）之差。GPST 采用美國海軍天文臺（USNO）維持的原子時，規定在1980－01－06 0：00與協調世界時（UTC）完全一致，與國際原子時（TAI）之差為19s。BDT 采用中國國家授時中心（NTSC）維持的原子時，在2006－01－01 0：00設置與UTC 一致，與TAI之差為33s［1］。雖然很多學者對系統時差的解算方法進行了深入研究［2－3］，但是對系統時差預報方法的研究較少。本文重點研究了BDS／GPS系統時差的組合實時預報方法，分析了改進的多項式預報模型、AR 模型以及組合實時預報模型和預報精度。

1 改進的多項式預報模型

短期的BDS／GPS系統時差時間序列具有線性或拋物線特性，且具有周期性變化趨勢，因此基于系統時差數據的多項式預報模型常采用一次或二次多項式模型（簡稱為MP）。本文采用的時差數據來源于上海天文臺，通過將接收機外接時間頻標，并扣除已校正的硬件時延偏差等，采用PPP技術解算，將能夠模型化的誤差采用模型扣除，不能模型化的誤差和時差參數一起估計，得到能夠反映BDS／GPS系統時差變化規律的時差數據。圖1為2013年第113～114d的BDS／GPS系統時差時間序列，呈線性變化，其他時間序列段的時差也呈現相似的規律。

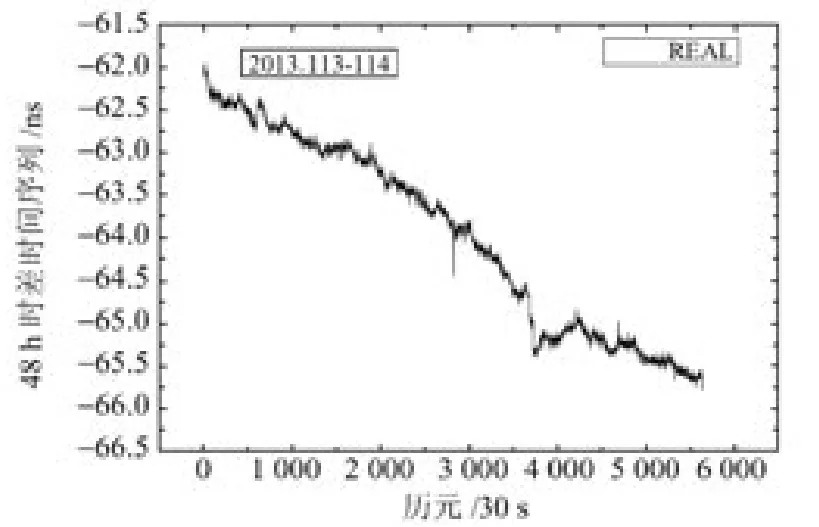
圖1 BDS／GPS系統時差時間序列Fig.1 BDS／GPS system time offset sequence

本文對多項式模型進行3方面改進：1）比較擬合數據段殘差的標準差來選擇一次多項式或二次多項式模型；2）采用快速傅里葉變換確定顯著周期項，進行周期項預報；3）根據離預報歷元遠近來確定觀測權矩陣以改進隨機模型，進而得到改進的多項式預報模型（簡稱MPP）［4］：

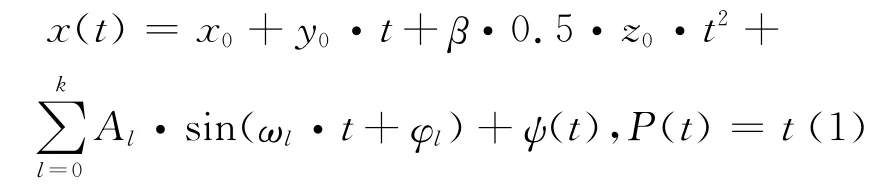
其中，t為歷元時間；x（t）為系統時差觀測值；x0為常數項參數，y0為一次項參數，z0為二次項參數；β取值為0或1（當一次多項式擬合殘差標準差小于二次多項式擬合標準差時，β為0；反之，β為1）；Al、ωl、φl分別為周期項的振幅、角速度、相位；ψ（t）為觀測殘差；P（t）為觀測值的權。

為分析改進多項式模型的預報精度，統計2013年第113、114d的多項式模型和改進多項式 模型的單天預報殘差，如圖2所示。

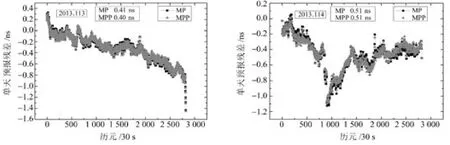
圖2 多項式模型和改進多項式模型預報殘差Fig.2 The predicting residual of MP and MPP

可以看出，多項式模型和改進多項式模型的預報殘差序列非常接近，第113d的改進多項式模型的預報精度比多項式模型提高了0.01ns，第114d的預報精度兩者相同，說明改進多項式模型的預報精度提高并不顯著。為了進一步分析兩種模型的預報精度，本文采用2013年第112～120d共9d的時差數據，統計多項式模型和改進多項式模型的單天時差預報精度以及最顯著周期項的影響（表1、2）。

表1 多項式模型和改進多項式模型的單天預報精度／nsTab.1 The 24－hour predicting precision of MP and MPP model／ns

從表1看出，改進多項式模型比多項式模型的單天時差預報精度改善較小，分別為0.420ns和0.417ns。為了揭示改進多項式預報模型單天時差預報精度改善較小的原因，統計了2013年111～119d最顯著周期項的周期和振幅（表2）。

表2 BDS／GPS系統時差最顯著的周期和振幅Tab.2 The most significant period and amplitude of BDS／GPS system time offset

從表2可知，這些天的周期項并不顯著，其振幅的均值為0.051ns，周期項改正對多項式模型預報精度的貢獻較小。當周期項較顯著時，周期項改正對多項式模型預報精度會有所提高。如第114d最顯著周期項的振幅為0.129ns，以第114 d為擬合數據，預報第115d的時差，單天時差預報精度提高了0.01ns，最明顯周期項為11.75h。這是由于衛星軌道周期約為0.5d［5－6］，隨著衛星的周期性運動，影響衛星鐘時間的外界環境呈現周期性變化，考慮到導航定位系統時間是由衛星鐘和地面鐘綜合得到紙面鐘［3］，因此系統時差的顯著周期多為11.75h。但是，由于衛星鐘還會受其他非周期性環境因素的影響，因此，系統時差的顯著周期會發生變化。

2 BDS／GPS系統時差的組合實時預報模型

Box和Jenkins將自回歸（AR）模型、移動平均（MA）模型和自回歸滑動平均（ARMA）模型有機地組合在一起，使之成為一種綜合的預測方法。ARMA 建模要求數據序列滿足平穩性，但在實際中數據序列往往呈現出趨勢性或周期性。這時，可以通過提取趨勢項和周期項或者是差分的方法對時間序列進行處理，使其滿足平穩性要求。基于差分后的數據序列建立的模型稱為ARIMA 模型［7－8］。本文采用改進的多項式模型以及一次差分后AR 模型建立組合實時預報模型。

2.1 組合實時預報模型的建立

提取趨勢項和周期項并進行一次差分后的系統時差數據序列可以認為是一組與時間相關的隨機變量，沒有確定的變化形式，不能用確定的函數描述，但可以用概率統計的方法尋求合適的隨機模型來近似反映其變化規律。實際上，模型僅通過系統時差的自身歷史觀測值來反映有關因素對預測時差的影響和作用。因此，AR 模型定義［9］為：

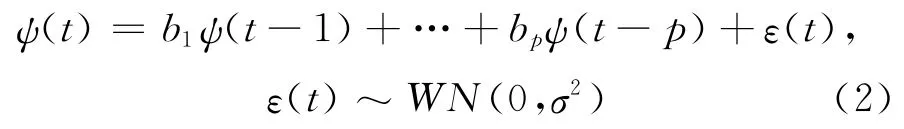
其中，t為歷元時間，ψ（t）為t時刻改進的多項式模型殘差，p為AR 模型的階數，ε（t）為AR 模型的觀測噪聲。

因此，BDS／GPS系統時差的組合實時預報模型（簡稱為MPP＋AR）可以描述為：

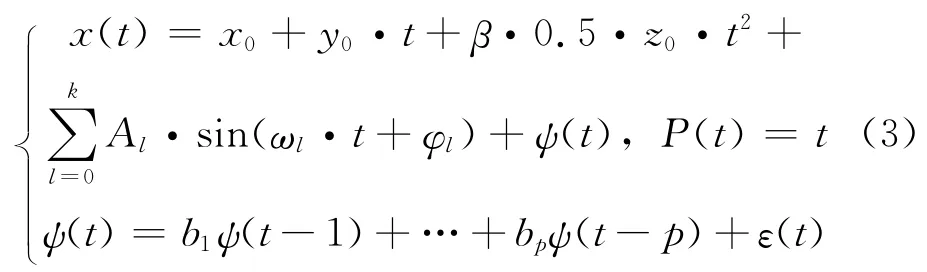
2.2 組合實時預報流程

BDS／GPS系統時差組合實時預報方法的實現流程如下：

1）采用多項式模型預報，直接得到多項式模型的預報結果以及預報殘差。

2）基于多項式模型，考慮二次項參數的自適應選取以及時間相關觀測權函數，進行多項式模型預報，得到扣除趨勢項的擬合殘差。基于此擬合殘差，利用快速傅里葉變換得到最顯著周期項，進而計算周期性預報殘差，得到改進的多項式模型預報結果以及預報殘差。

3）對扣除周期項的擬合殘差作一次差分，得到滿足平穩性的擬合殘差。在此基礎上進行AR模型預報，得到差分后的預報殘差。然后將其恢復得到AR 模型預報殘差，結合改進的多項式模型預報結果，得到組合預報模型的預報結果以及預報殘差。

2.3 組合實時預報流程的實現

基于BDS／GPS 系統時差實時監測數據，采用改進的多項式模型預報，獲得其擬合殘差，如圖3所示。改進多項式模型的擬合殘差已經去除了趨勢性和周期性，進行一次差分，獲得滿足平穩特性的差分數據。然后，基于差分后的數據擬合出AR 模型，從而獲得基于差分數據的AR 模型擬合預報時差（圖4）。圖5展示了擬合預報中間部分的若干歷元。可以看出，基于差分數據的AR模型的預報值隨著預報時間的增加而趨于恒定。

以改進多項式模型擬合殘差的最后一個歷元為起點，將基于一次差分數據的AR 模型預報值累加到該起點，得到AR 模型的預報值（圖6）。利用此修正值對改進多項式模型的預報結果進行修正，從而得到組合實時預報模型的預報時差（圖7）。可以看出，組合實時預報模型的單天預報精度優于改進多項式模型，分別為0.51ns 和0.29ns。

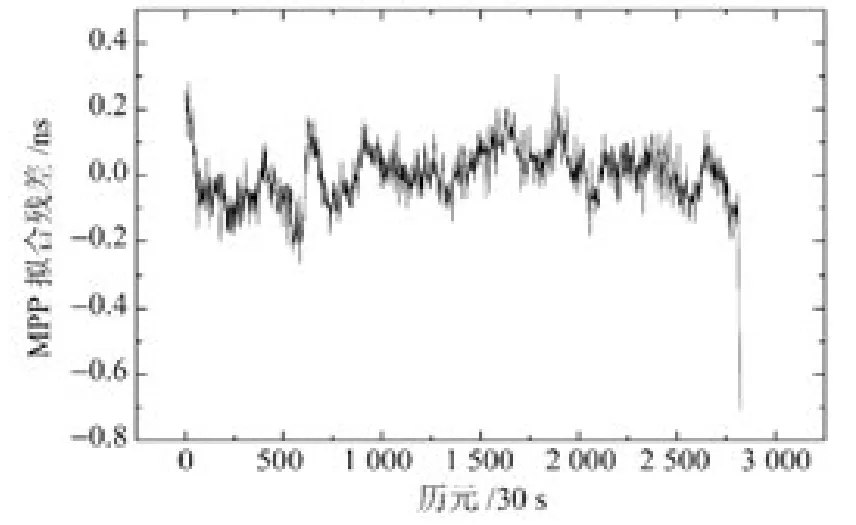
圖3 改進多項式模型的擬合殘差Fig.3 The fitting residual of MPP

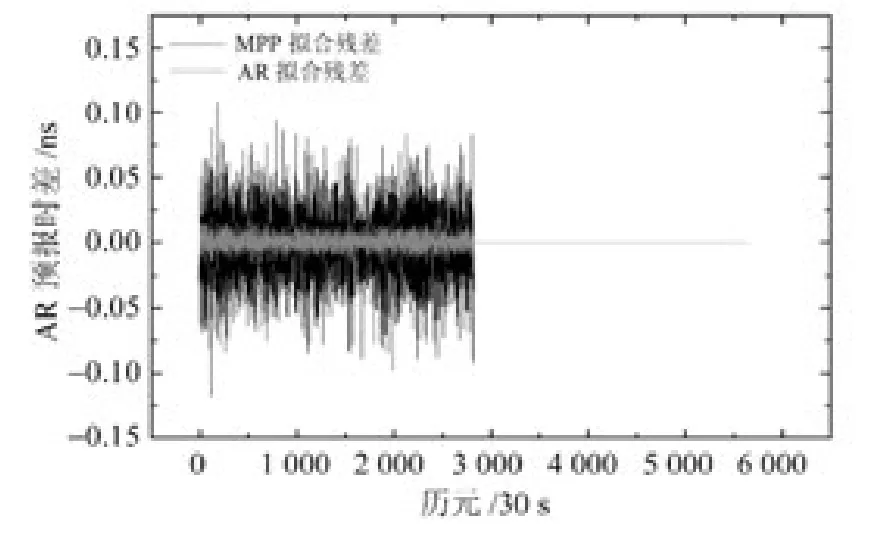
圖4 基于差分數據的AR 模型擬合預報時差Fig.4 The fitting and predicting system time offset of AR model with different data

圖6 AR 模型的預報時差Fig.6 The predicting system time offset of AR model

圖7 改進多項式模型和組合實時預報模型預報殘差Fig.7 The predicting residual of MPP and MPP＋AR model

考慮到改進多項式模型擬合殘差的最后一個歷元可能會出現粗差，對AR 預報模型進一步優化。其主要思想是：改進多項式模型擬合殘差的最后一個歷元偏離擬合殘差絕對值的均值較大時，組合實時預報模型直接采用改進多項式模型；否則，采用距離擬合殘差絕對值的均值最小的擬合殘差且最靠后的歷元作為AR模型預報起點進行預報。如圖8所示，方形曲線為BDS／GPS系統時差原始數據，圓形曲線為模型優化前的預報結果，三角形曲線為模型優化后的預報結果。可以看出，模型優化后的預報結果更接近于真實時差數據。

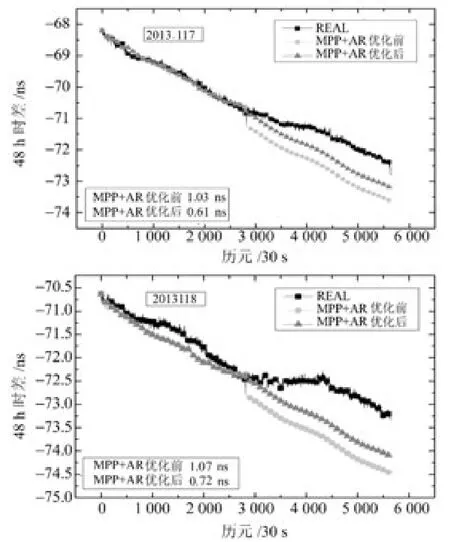
圖8 優化后的組合實時預報模型預報結果Fig.8 The predicting results of combined real－time model after optimization

3 組合實時預報模型精度分析

因篇幅限制，本文僅統計了2013年第112～120d的組合實時預報模型與多項式預報模型的單天時差預報精度，以分析組合實時預報模型精度和可靠性，如圖9、表3所示。

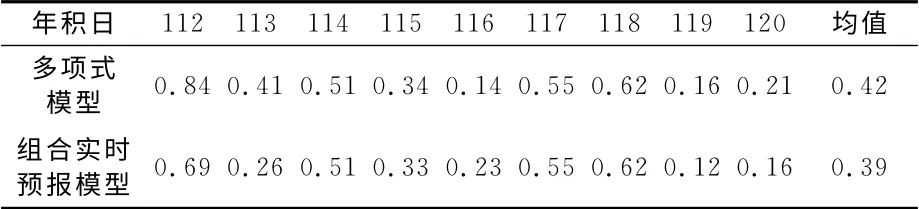
表3 組合實時時差預報模型和多項式模型的單天預報精度／nsTab.3 The 24－hour predicting precision of combined realtime model and MP model／ns

可以看出，采用組合實時預報模型的預報精度為0.39ns，比多項式模型提高了0.03ns，但組合實時預報模型的預報精度更加穩定，僅有1d的預報精度差于多項式模型，其他天均優于或等于多項式模型。

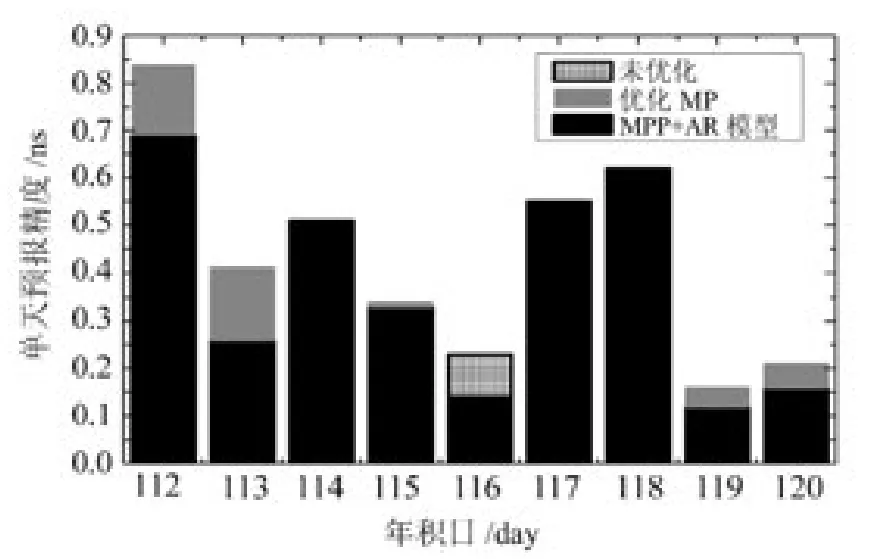
圖9 組合實時時差預報模型和多項式模型的單天預報精度統計Fig.9 The 24－hour predicting precision of combined real－time model and MP model

4 結 語

本文構建的BDS／GPS 系統時差預報模型，考慮了時差序列的時鐘參數特性、周期性以及隨機補償特性等，單天的時差預報精度優于0.4ns，優于傳統的多項式模型；同時在算法穩定性方面，也顯著優于傳統的多項式模型。該模型同樣適用于其他導航系統之間的實時時差預報。然而，實時時差預報數據預處理時要考慮粗差和鐘跳等異常探測，在建立模型時也需要考慮兩個系統實際上的物理時鐘變化特性，這也是作者下一步的研究重點。

［1］孔祥元，郭際明，劉宗泉.大地測量學基礎［M］.武漢：武漢大學 出 版 社，2010（Kong Xiangyuan，Guo Jiming，Liu Zongquan.Foundation of Geodesy［M］.Wuhan：Wuhan University Press，2010）

［2］朱琳，張慧君，李孝輝，等.全球衛星導航系統時差監測與修正方法研究［C］.第4屆中國衛星導航學術年會，武漢，2013（Zhu Lin，Zhang Huijun，Li Xiaohui，et al.Monitoring and Correction Method of the System Time Offset of Global Navigation Satellite System［J］.The 4th China Satellite Navigation Conference，Wuhan，2013）

［3］陳俊平，張益澤，藺玉亭，等.一種單站多衛星系統時差監測的新方法［C］.第4 屆中國衛星導航學術年會，武漢，2013（Chen Junping，Zhang Yize，Lin Yuting，et al.Precise GNSS Timing Bias Estimation Based on Single Multi－GNSS Station［J］.The 4th China Satellite Navigation Conference，Wuhan，2013）

［4］Huang G W，Zhang Q，Xu G C.Real－time Clock Offset Prediction with an Improved Model［J］.GPS Solutions，2014，18（1）：95－104

［5］Heo Y J，Cho J，Heo M B.Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behavior［J］.Measurement Science and Technology，2010，21（7）：190－190

［6］Senior K，Ray J，Beard R L.Characterization of Periodic Variations in the GPS Satellite Clocks［J］.GPS Solution，2008，12（3）：211－225

［7］楊元喜，崔先強.動態定位有色噪聲影響函數——以一階AR 模型為例［J］.測繪學報，2003，32（1）：6－10（Yang Yuanxi，Cui Xianqiang.Influence Functions of Colored Noises on Kinematic Positioning－Taking the AR Model of First Class as an Example［J］.Acta Geodaetica et Cartographica Sinica，2003，32（1）：6－10）

［8］徐君毅，曾安敏.ARIMA（0，2，q）模型在衛星鐘差預報中的應用［J］.大地測量與地球動力學，2009，29（5）：116－120（Xu Junyi，Zeng Anmin.Application of ARIMA（0，2，q）Model to Predication of Satellite Clock Error［J］.Journal of Geodesy and Geodynamics，2009，29（5）：116－120）

［9］張清華，隋立芬，牟忠凱.基于小波與ARMA 模型的衛星鐘差預報方法［J］.大地測量與地球動力學，2010，30（6）：100－104（Zhang Qinghua，Sui Lifen，Mu Zhongkai.A GPS Precise Clock Errors Prediction Model Based on Wavelet and ARMA［J］.Journal of Geodesy and Geodynamics，2010，30（6）：100－104）