數學中對稱式結論的合理擴展

樸麗莎，葛仁東

(1.云南大學 滇池學院，云南 昆明650228;2.大連民族大學 理學院，遼寧 大連116605)

理解和應用低維低階的數學結論是較為容易的，但由于處理實際問題的復雜性，往往需要使用高維空間或高階的數學結論。本文以Bézier 曲線為例，提出合理對稱模式直接擴展的新方法，即借助Bézier 曲線低階對稱矩陣形式的方程，通過二項式定理的展開式系數找尋規律，直接擴展到高階方程情形，進而建立了n 階Bézier 曲線方程，并對擴展結果予以證明。另外，通過舉例說明了數學學科中也存在很多類似的結論。

1 Bézier 曲線的合理擴展

Bézier 曲線是計算機輔助幾何設計中最常用的曲線之一，是由法國雷諾汽車公司的工程師Bézier 在上世紀60 年代提出的。該方法采用折線組成的多邊形來定義一條曲線，設計者先用折線多邊形描繪這條曲線的大致輪廓，再用Bézier 曲線表達式產生一條光滑的曲線［1］。

Bézier 曲線有不同的數學定義形式，如de Casteljau 遞歸算法、Bernstein 多項式基函數，其中用控制頂點定義的Bernstein 基［2］表示形式容易理解，且應用廣泛，本文將針對該參數多項式形式進行方程的建立和結論的證明。

1.1 Bézier 曲線的建立

由兩點p0，p1可以確定一條一次Bézier 曲線，方程為p(t)=p0+(p1－p0)t，t∈［0，1］。為了找到比較容易擴展的對稱式曲線方程，根據文獻［3］可以將方程改寫成如下矩陣形式:

式中，B0，1(t)=1 － t，B1，1(t)=t，記M=是對稱矩陣。

用此方法繼續寫出三點二次Bézier 曲線方程，進而擴展n 次方程。由p0，p1，p2確定的二次Bézier 曲線為

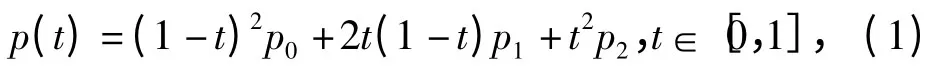
令

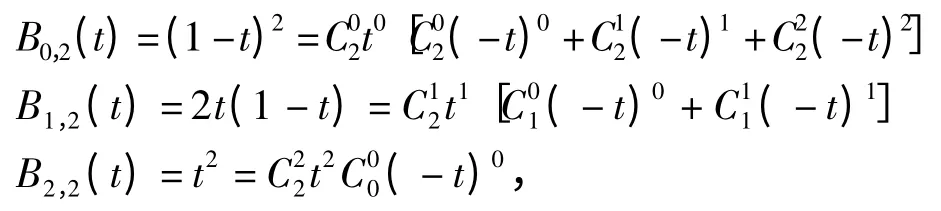
則式(1)可改寫成

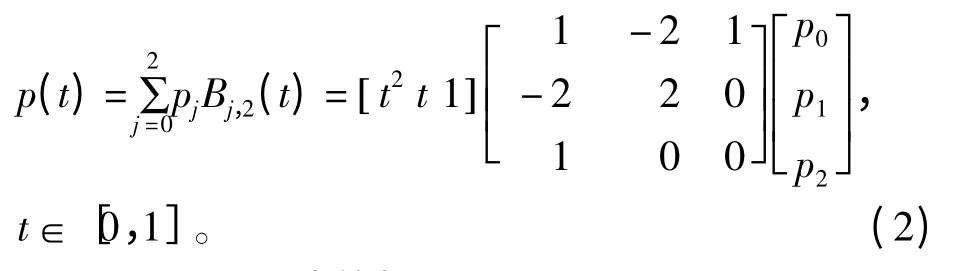
1.2 Bézier 曲線的擴展及證明

由前小節的分析可得如下結論。

定理 式(1)和式(2)對稱矩陣中的元素依次為二項式［(1 － t)+ t］n展開式中關于t 的系數，故可直接將對稱矩陣擴展進而得到n 次Bézier曲線方程

證明 要證明Bézier 曲線可表示成式(3)，即證明

Mn+1=(bi+1，j+1)n+1是n+1 階對稱方陣

因為

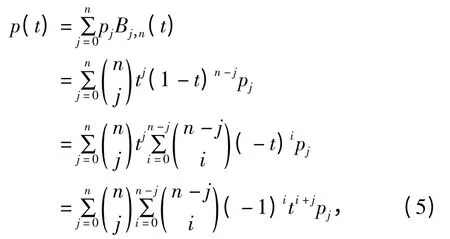
令i+j=s，則式(5)

故有

當0 ≤i + j ≤n 時，bi+1，j+1=(－ 1)n－i－j=(－1)n－i－j。

證畢。

上述分析說明，對于復雜的數學結論，如果可以找到合理的對稱形式，就存在向高階高維擴展的可能性，并且由直接擴展得到的結論從形式上呈現對稱性，內容上規律性、緊湊性強，這些優點更有利于數學結論的理解和應用。接下來給出直線方程問題和函數插值問題，說明合理擴展對稱式方程這一方法的一般性。

2 舉 例

2.1 由平面直線到空間直線

在平面上任取兩點(x1，y1)和(x2，y2)，兩點所確定的直線斜率k=(x2≠x1)，故點斜式方程y－y1=k(x－x1)。將方程改寫為對稱式

設想由平面到空間，也就是二維擴展到三維，具體到每一個點，原有的坐標分量由2 個變成3個。那么，根據前文的合理擴展想法，平面對稱式方程(4)就可以直接擴展為由空間兩點(x1，y1，z1)和(x2，y2，z2)確定的直線方程

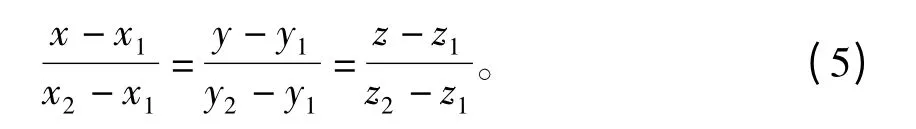
對式(5)的驗證詳見文獻［4］。

2.2 由一階插值到高階插值

插值法是在生產實踐中提煉而成的方法，主要是通過離散樣本點作一條通過這些點的光滑曲線，以便滿足設計要求或進行加工。

以Lagrange 插值多項式為例，設兩個節點(x0，y0)，(x1，y1)則可以確定一次插值多項L1(x)=a0+a1x，由插值條件

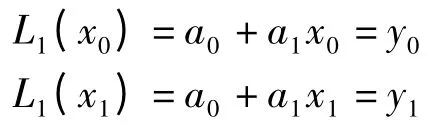
可以聯立解出待定參數a0=。

所以，兩個節點的一次插值多項式為L1(x)=。

將其改寫成如下對稱形式:

不難發現兩個線性函數滿足

也就是li(x)(i=0，1)在對應的插值點xi處取值為1，在其他節點處取值為0。由此，可以設想通過擴展li(x)進而將式(6)擴展成高階插值。那么n+1 個節點的n 次插值多項式的形式為

由此說明li(x)(i=0，1，...，n)的存在性進而證明式(7)擴展的合理性。n 次多項式li(x)(i=0，1，...，n)滿足li(xj)=，有n 個根xj(j=0，1，...，n，j≠i)，且li(xi)=1，故它必定如下形式:

代入式(7)后可以證明Ln(x)滿足插值條件［5］。

3 結 語

本文主要通過建立并擴展Bézier 曲線的對稱矩陣式方程，提出了復雜數學結論可以借助合理對稱形式向高階高維擴展的方法。另外，通過直線方程和函數插值的舉例驗證了數學中確實存在一些對稱式結論可以直接進行合理擴展，并且擴展得到的結論更有助于理解和應用。相信在數學學科中，還有很多這樣的例子。但是，并不是所有的對稱式結論都可以擴展，在接下來的研究中對稱形式的數學結論可以擴展的條件和適用范圍將是亟待解決的問題。

［1］顧蘭智，方憶湘. Bézier 曲線繪制程序的開發［J］. 電腦開發應用，2008(9):34 －35.

［2］何援軍.幾何計算［M］.2 版.北京:高等教育出版社，2013:301 －330.

［3］葛仁東，張艷茹，趙玲玲，等. 體育館頂部外形設計的數值模擬［J］.大連民族學院學報，2009(1):27 －29.

［4］呂林根，許子道.解析幾何［M］.4 版.北京:高等教育出版社，2006:112 －119.

［5］丁麗娟，程杞元.數值計算方法［M］.2 版.北京:北京理工大學出版社，2011:101 －106.