次態(tài)卡諾圖在時序邏輯電路自啟動設(shè)計中的應(yīng)用*

高美蓉

(寶雞文理學(xué)院 物理系，陜西 寶雞 721001)

次態(tài)卡諾圖在時序邏輯電路自啟動設(shè)計中的應(yīng)用*

高美蓉

(寶雞文理學(xué)院 物理系，陜西 寶雞 721001)

摘要：時序邏輯電路的設(shè)計過程中，電路是否能夠自啟動是必須考慮的問題，也是數(shù)字電子技術(shù)課程教學(xué)的重點和難點內(nèi)容。通過詳細(xì)分析電路不能自啟動的原因，提出了利用卡諾圖消除不能自啟動的問題，修改次態(tài)卡諾圖，為次態(tài)卡諾圖中的無效狀態(tài)指定次態(tài)，指定的次態(tài)屬于有效循環(huán)狀態(tài)。利用該方法實現(xiàn)了邏輯電路的自啟動。

關(guān)鍵詞：卡諾圖；自啟動；無效循環(huán)；時序邏輯電路

在時序邏輯分析設(shè)計和電子技術(shù)教學(xué)活動中，時序邏輯電路的自啟動是經(jīng)常遇到的一個實際問題，而且是數(shù)字電子技術(shù)基礎(chǔ)教學(xué)中的重點和難點內(nèi)容。在時鐘信號clk的控制下，時序邏輯電路即使處在無效狀態(tài)，也可以自動過渡到有效狀態(tài)，不會在多個無效狀態(tài)間形成無效循環(huán)，這樣的電路稱為自啟動電路；如果在無效狀態(tài)間形成循環(huán)，這樣的電路則稱為不能自啟動的時序電路。然而，檢查電路能否自啟動一般發(fā)生在整個設(shè)計結(jié)束時，如果發(fā)現(xiàn)電路不能自啟動，而設(shè)計又要求電路能自啟動，這就要修改電路設(shè)計，重新畫電路，如此循環(huán)，效率極低。如何對電路進行更改，沒有具體的規(guī)定，方法靈活。本文介紹利用卡諾圖設(shè)計，可以事先指定無效狀態(tài)直接或間接地進入有效循環(huán)，即為無效狀態(tài)指定次態(tài)，從而實現(xiàn)自啟動。

1電路不能自啟動的原因

在設(shè)計時序邏輯電路時，要求根據(jù)給出的具體邏輯問題，求出實現(xiàn)這一邏輯功能的邏輯電路。因為設(shè)計結(jié)果應(yīng)力求簡單，所以在設(shè)計同步時序邏輯電路時，一般按下述步驟進行設(shè)計：1)邏輯抽象，得出電路的狀態(tài)轉(zhuǎn)換圖或狀態(tài)轉(zhuǎn)換表；2)狀態(tài)化簡，得出最簡狀態(tài)圖；3)確定狀態(tài)數(shù)，進行狀態(tài)分配；4)選擇觸發(fā)器的類型，求出電路的驅(qū)動方程、輸出方程和狀態(tài)方程；5)根據(jù)驅(qū)動方程，畫出邏輯電路圖；6)檢查設(shè)計的電路能否自啟動。

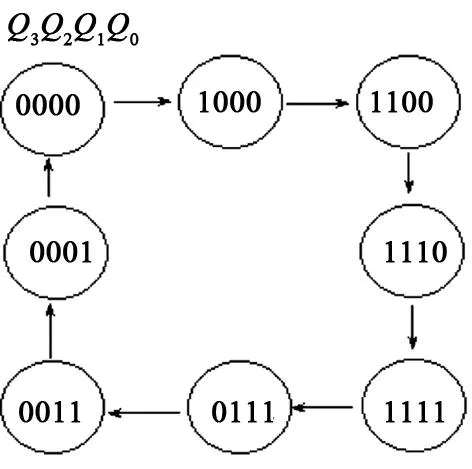
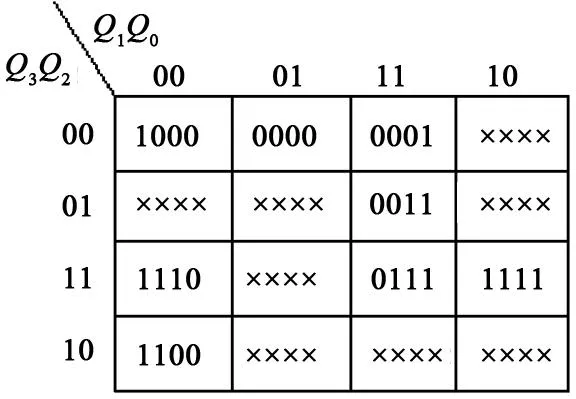
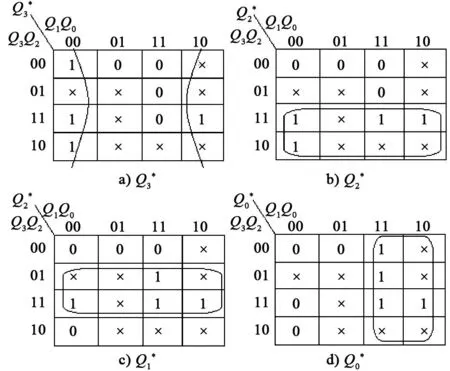
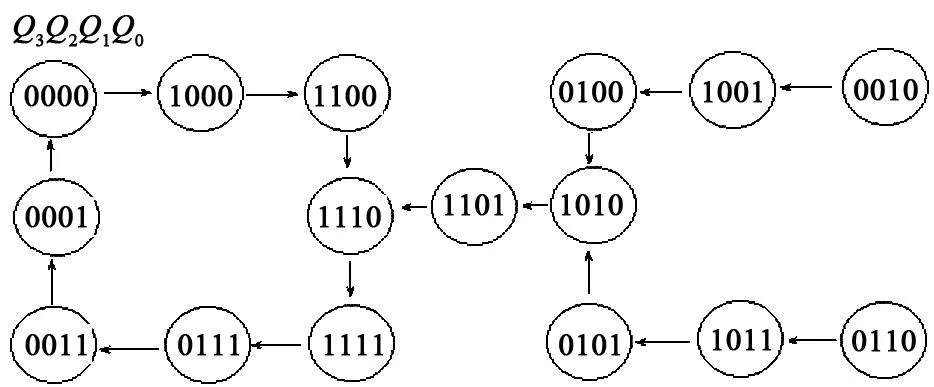
電路的自啟動問題源于狀態(tài)分配和狀態(tài)方程確定的過程中[1-2]。在狀態(tài)分配過程中，時序邏輯電路的狀態(tài)是用觸發(fā)器狀態(tài)的不同組合來表示的。首先需要確定觸發(fā)器的數(shù)目n，如果實際狀態(tài)數(shù)為M，選用的觸發(fā)器個數(shù)n必須滿足2n-1

2利用卡諾圖消除不能自啟動的問題

時序邏輯電路的設(shè)計步驟，以能得出最簡表達式為原則處理每項取值，而忽視無效狀態(tài)取值是否能滿足自啟動的條件[3]，沒有兼顧無效狀態(tài)是否能滿足自啟動的因素。解決的方法是應(yīng)同時考慮邏輯最簡化和自啟動的要求，來確定約束項的具體取值。也就是在某種程度上舍棄一些項簡化，來滿足必要的自啟動。下述結(jié)合實例介紹修正設(shè)計的方法。

例如：設(shè)計一個能自啟動的4位扭環(huán)形計數(shù)器。要求它的有效循環(huán)狀態(tài)為0000→1000→1100→1110→1111→0111→0011→0001→0000。根據(jù)要求的狀態(tài)循環(huán)，可以得到電路的狀態(tài)轉(zhuǎn)換圖(見圖1)，根據(jù)圖1(8個狀態(tài)以外的狀態(tài)為無效狀態(tài))畫出電路的次態(tài)卡諾圖(見圖2)。

圖1　電路的狀態(tài)轉(zhuǎn)換圖

圖2　電路的次態(tài)卡諾圖

圖3　次態(tài)卡諾圖的分解圖

如果單純地追求化簡結(jié)果最簡單，化簡后的狀態(tài)方程表示為：

將Q3、Q2、Q1、Q0的8個無效狀態(tài)1010、1101、0110、1011、0101、0010、1001和0100分別帶入化簡后的狀態(tài)方程中求出次態(tài)，即得到電路的狀態(tài)轉(zhuǎn)換圖(見圖4)。可以看出這樣設(shè)計的電路是不能自啟動的[5-6]，原因是在利用卡諾圖化簡的過程中，如果把表示任意項的×包含在圈內(nèi)，就等于把×取值為1，如果把表示任意項的×包含在圈外，就等于把×取值為0，這就相當(dāng)于已經(jīng)為無效狀態(tài)指定了次態(tài)。如果這個指定的次態(tài)屬于有效循環(huán)中的狀態(tài)，那么電路就能夠自啟動；反之，如果次態(tài)還是無效狀態(tài)，則電路就不能夠自啟動。該電路就屬于后者，指定的次態(tài)仍然屬于無效狀態(tài)。這就需要修改狀態(tài)方程的化簡方式，將無效狀態(tài)的次態(tài)改為某個有效狀態(tài)。

圖4　電路的狀態(tài)轉(zhuǎn)換圖

圖5　修改后的卡諾圖

圖6　修改后的電路狀態(tài)轉(zhuǎn)換圖

經(jīng)分析可知，如果僅從能啟動的角度考慮，將1101的次態(tài)指定為1110，可以保證電路能自啟動。0101狀態(tài)的次態(tài)本不必修改，它可以經(jīng)過6個時鐘脈沖信號進入到有效循環(huán)，而0110經(jīng)過8個時鐘脈沖信號進入到有效循環(huán)。將0101的次態(tài)指定為1010，0110進入無效狀態(tài)時經(jīng)過5個時鐘脈沖信號就可以進入有效循環(huán)，0101經(jīng)過3個時鐘脈沖信號就可以進入有效循環(huán)。而且邏輯式可以更加簡單，修改后的狀態(tài)方程為：

若選用D觸發(fā)器組成這個計數(shù)器，則驅(qū)動方程為：

按照上式畫出邏輯電路圖(見圖7)，這個電路一定能夠自啟動。狀態(tài)轉(zhuǎn)換圖如圖6所示。

圖7　D觸發(fā)器構(gòu)成的能自啟動的4位　扭環(huán)形計數(shù)器的邏輯電路圖

3結(jié)語

綜上所述，本文分析了時序邏輯電路不能自啟動的原因，以及如何解決該問題，即通過修改卡諾圖解決時序邏輯電路設(shè)計過程中的自啟動問題。在修改卡諾圖過程中，在無效狀態(tài)不止1個的情況下，為保證電路能夠自啟動，應(yīng)使每個無效狀態(tài)都能直接地或間接地轉(zhuǎn)為某1個有效狀態(tài)[7]。在將無效狀態(tài)的次態(tài)轉(zhuǎn)為有效狀態(tài)時，究竟取哪個有效狀態(tài)，應(yīng)該根據(jù)得到的狀態(tài)方程是否最簡單而定。這就需要利用課余時間多思考、多總結(jié)和多歸納，只有這樣才能滿足電路最簡單并且能夠自啟動。

參考文獻

[1] 閻石.數(shù)字電子技術(shù)基礎(chǔ)[M]. 4版. 北京：高等教育出版社，1998.

[2] 康華光.電子技術(shù)基礎(chǔ)：數(shù)字部分[M]. 3版. 北京:高等教育出版社,1988.

[3] 張海泉.時序邏輯電路的自啟動研究[J]. 河南教育學(xué)院學(xué)報，2005(14)：33-34.

[4] 李正發(fā). 對時序邏輯電路自啟動設(shè)計的探討[J]. 湖北第二師范學(xué)院學(xué)報，2008(25): 67-68.

[5] 騰香.基于次態(tài)卡諾圖的移位寄存器型計數(shù)器的自啟動設(shè)計[J].浙江大學(xué)學(xué)報，2011(38):419-423.

[6] 汪學(xué)典. 卡諾圖在時序邏輯電路自啟動設(shè)計中的應(yīng)用[J]. 武漢化工學(xué)院學(xué)報,1995(17):58-61.

[7] 夏強勝,李娟. 卡諾圖在時序邏輯電路自啟動教學(xué)中的應(yīng)用[J]. 安慶師范學(xué)院學(xué)報：自然科學(xué)版,2013(5):128-30.

* 寶雞文理學(xué)院院級重點項目(ZK14066)

責(zé)任編輯鄭練

Since the Next State Map of Kano to Start the Application in the Design of Sequential Logic Circuit

GAO Meirong

(Physics Department of Baoji College of Arts and Sciences, Baoji 721016, China)

Abstract：In the design process of sequential logic circuit, the circuit is the key part of the digital electronic technology course. Through the detailed analysis of the circuit, we prove that using Karnaugh map can’t eliminate the slef-starting problems. Modify the next state Karnaugh map for next state Karnaugh map in the invalid state designated of secondary state, and the designated secondary state belongs to the effective cyclic state. Using this method to achieve logic circuit from the start is proposed at last.

Key words:Karnaugh map, self starter, invalid cycle, sequential logic circuit

收稿日期：2015-02-09

作者簡介：高美蓉(1980-)，女，碩士，講師，主要從事應(yīng)用電子技術(shù)等方面的教學(xué)與研究。

中圖分類號：TN 79

文獻標(biāo)志碼:B