基于簡單占空比調節的異步電機直接轉矩控制

李政學 張永昌 李正熙 班曉娟 楊海濤

（1.北京科技大學計算機與通信工程學院 北京 100083

2.北京市電力電子與電氣傳動工程研究中心（北方工業大學） 北京 100144）

1 引言

迄今為止，磁場定向控制（Field Oriented Control,FOC）和直接轉矩控制（Direct Torque Control，DTC）已經成為在高性能交流調速領域中兩種最為常用的方法[1]。相比于磁場定向控制，直接轉矩控制在靜止的定子坐標系中進行計算，無需旋轉坐標變換，電流調節器和脈寬調制模塊[1-4]；它使用兩個滯環比較器和一個開關表，根據磁鏈和轉矩的瞬時誤差選擇使定子磁鏈和轉矩向各自的給定值變化的電壓矢量，具有非常簡單的結構和快速的動態轉矩響應能力[5]。另外，DTC 在運算中使用的電機參數非常少，大大減小了電機參數波動對控制性能的影響。

傳統DTC 的一個顯著缺點是輸出轉矩脈動大、開關頻率不恒定。空間矢量調制（SVM）技術可以有效地解決這個問題[6,7]。SVM 技術的基本思想是，在每一個控制周期中，通過計算得到一個能夠恰好補償當前定子磁鏈和轉矩誤差的電壓矢量。該電壓矢量可以用兩個相鄰的有效電壓矢量和零電壓矢量合成得到。這種基于SVM 技術的DTC 算法可以極大地減小輸出轉矩的脈動，同時獲得了恒定的開關頻率。但是，它的計算量非常大，而且使用了更多的電機參數。雖然控制性能有所提高，卻喪失了DTC 控制結構簡單的優點。

另一種減小轉矩脈動的方法是采用占空比控制（duty ratio control）技術，該方法與SVM 技術相比復雜性有所降低。它的基本思想是，在每個采樣周期中，有效電壓矢量只作用一部分時間，剩余時間選擇零電壓矢量。針對如何確定每個采樣周期中有效電壓矢量作用時間的問題，提出了多種方法。其中最有代表性的三種方法是[8-12]：①無差拍控制；②平均轉矩控制；③轉矩脈動最小控制。另外，還可以采用模糊邏輯自適應方法[13-15]來獲得占空比。這些方法獲得了很好的控制性能，但是通常計算量較大，并且嚴重依賴電機參數。

最近，模型預測控制（MPC）在電機高性能控制中得到了廣泛研究和關注[16-19]。這種方法與DTC的相似之處是都直接選擇最終電壓矢量，但 MPC選擇矢量時是依賴于系統模型和評價函數，而非DTC 中的矢量表。比如文獻[16]通過對每個可能開關狀態代價函數的評估，選擇最能滿足性能要求的電壓矢量輸出。文獻[17]提出一個三電平逆變器饋電的DTC 方案，它使用多步預測取得開關頻率的減小，同時控制轉矩、磁鏈和中點電位在各自的滯環帶內。MPC 相比DTC 有更好的穩態性能，但是計算量大，對模型和參數的精度要求較高。

DTC 需要對定子磁鏈進行估計，本文采用基于全階觀測器的方法估計磁鏈[20-22]，只需兩路直流母線電壓和兩路電機電流信號，可以在全速域范圍內準確地觀測磁鏈，并成功地將觀測得到的磁鏈用于閉環DTC 中。

目前針對異步電機而言，還沒有文獻對各種占空比控制方法進行過比較研究。本文首先在詳細比較三種典型占空比確定方法性能的基礎上，提出一種簡單而非常有效的占空比確定方法。該方法保持了傳統DTC 的結構簡單性，在占空比確定中考慮對轉矩和磁鏈誤差的同時優化，獲得了同時減小轉矩和磁鏈脈動的良好性能。為了進一步改善系統性能，使用基于全階觀測器的方法觀測定子磁鏈，可以在全速域范圍內準確的觀測磁鏈。仿真和實驗結果證明了本文所提方法的可行性和在減小轉矩和磁鏈脈動方面的有效性。

2 異步電機的數學模型

2.1 電機方程

在d-q 靜止坐標系中，利用空間矢量表示的電機方程為

式中 ψs，ψr——定子和轉子的磁鏈矢量；

us——定子電壓矢量；

is，ir——定子和轉子電流矢量；

ωr——轉子的電角速度；

Ls，Lr——定子和轉子的自感；

Lm——互感；

Rs，Rr——定子和轉子的電阻。

由式（1）～式（4）得到使用定子和轉子磁鏈矢量作為狀態變量的異步電機狀態方程為

電磁轉矩可以使用定子和轉子磁鏈矢量的叉積表示為

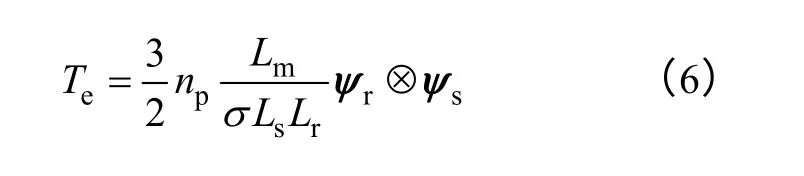
式中 np——電機的極對數；

2.2 電壓矢量對轉矩和磁鏈的影響

標準的兩電平電壓源逆變器（VSI）的輸出只有8 種電壓矢量，包括6 個有效電壓矢量（V1～V6）和2 個零電壓矢量（V0,V7）。根據有效電壓矢量的位置，坐標平面分為6 個扇區，如圖1 所示。

對于電壓源逆變器饋電的DTC 系統，電壓矢量是唯一的可控制的輸入變量，因此希望解析推導出轉矩和磁鏈變化量與電壓矢量之間的關系。

圖1 8 個電壓矢量和6 個扇區 Fig.1 8 voltage vectors and 6 sectors

由式（6）求解轉矩對于時間t 的微分可得

將式（5）代入式（7），經過推導最終得到轉矩微分為

式中，⊙表示矢量點積。

從式（8）可以看出轉矩微分由3 部分構成：第一部分ΔTe1與轉矩成反比；第二部分ΔTe2與轉速相關；最后一部分ΔTe3反映了定子電壓矢量對轉矩的影響。

當選擇零電壓矢量時，轉矩微分變為

從式（9）中可以看出，零電壓矢量一般導致負的轉矩變化。

如果時間間隔非常短，并且在忽略定子電阻壓降的情況下，式（1）可以改寫為

由式（10）可以看出，在一個極短的時間段內，作用某一電壓矢量后所產生的定子磁鏈矢量的改變量，與該電壓矢量具有相同的方向；如果能夠合理控制作用于電機的合成電壓矢量us的大小，就能控制磁鏈的變化量，使磁鏈的誤差控制在磁鏈滯環帶寬內，這也正是傳統DTC 的基本原理。

在傳統DTC 中，滯環比較器不區分轉矩和磁鏈誤差的大小，從開關表中選出的電壓矢量將作用于整個采樣周期。在轉矩誤差較小的周期中，轉矩很快達到參考值，之后繼續增大或減小，導致了較大的轉矩脈動。占空比控制技術的應用可以解決這個問題，在占空比控制中，所選的有效電壓矢量只在該采樣周期中作用一部分時間，而剩余的時間選擇零電壓矢量。有效電壓矢量作用時間占采樣周期時間的比率稱作占空比d，其取值范圍是0～1。

3 經典的占空比確定方法

3.1 基本原理

由（8）式看出，通過調整電壓矢量us的幅值和作用時間可以改變轉矩的大小。電壓矢量的幅值是由直流母線電壓決定，通常是固定的，而us的作用時間可以由零變化到整個采樣周期，這等效于改變了電壓矢量的長度。從式（9）看出，零電壓矢量只能減小轉矩，而合適的有效電壓矢量能增大轉矩，因此，在一個采樣周期中同時使用零電壓矢量和有效電壓矢量可以減小轉矩脈動。關鍵問題是如何決定這兩個電壓矢量的作用時間，或者說確定有效電壓矢量的占空比。

3.2 經典占空比確定方法

三種經典占空比確定方法如圖2 所示。

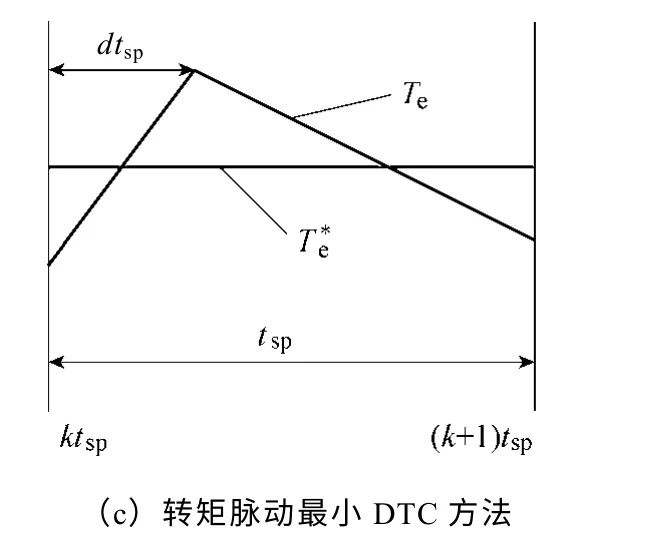
圖2 三種經典占空比確定方法原理 Fig.2 Basic principle of the three classical duty ratio determination methods

方法1 期望瞬時電磁轉矩在該采樣周期末等于參考值，如式（11）所示，稱之無差拍控制[8-10]。

現有文獻[8,9]致力于磁鏈和轉矩同時無差拍控制，為此需要求解一個二次方程式，其求解過程和結果表達式都相對復雜，而且對電機參數依賴性較強。為了減低算法復雜性，本文僅考慮轉矩無差拍控制。

方法2 致力于使整個采樣周期的平均電磁轉矩等于參考值，如式（12）所示，也叫直接平均轉矩控制[11]。

方法3 是使轉矩脈動的方均根值（RMS）在一個采樣周期中最小[12]，表達式為

在一個很小的采樣周期tsp內，因為磁鏈和轉速的變化相對很慢，可以假設由式（8）和式（9）計算出的有效電壓矢量的上升斜率f1和零電壓矢量的下降斜率f2為常數。在這種假設條件下，通過求解式（11）～式（13）可得三種經典占空比確定方法中有效電壓矢量的作用時間為

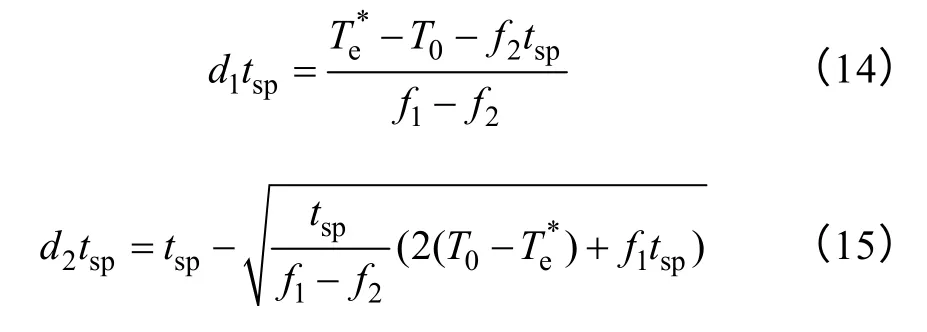
式中 T0——第k 個采樣時刻的初始轉矩；

d1,d2,d3——方法1、2、3 中有效電壓矢量的占空比。

4 基于新占空比控制的DTC 方法

4.1 現有占空比方法的比較

從式（14）～式（16）所示的三種占空比確定方法表達式可以看出，雖然它們具有不同的形式，然而，有文獻報道稱與傳統DTC 相比都獲得了更好的性能。除了解析方法，還有模糊邏輯自適應方法[13-15]，文獻[13-15]中也報道說相比于傳統 DTC轉矩脈動明顯減小。這些方法都啟示如何獲得確定占空比的方法并不重要，最重要的是必須使用零電壓矢量，因此有可能采用更為簡單的占空比控制方法來提高DTC 的性能。

4.2 新占空比方法原理

經典占空比確定方法如式（14）～式（16）所示，計算復雜并且對電機參數依賴大。其中，表達式（15）非常復雜，甚至需要計算開平方項。而式（14）和式（16）則比較相似，區別僅在分子和分母中第一項的系數。由這些不同占空比方法在表達式上的差異性啟發可以做出更大膽的假設，即令式（14）～式（16）中的分母為常數，從而消除對電機參數的依賴性。換句話說，可以近似認為這是幾種不同占空比方法的“混合”。由于使用零電壓矢量可以減小轉矩脈動，而對于占空比的確定方法似乎還沒有統一的要求。本文在大量仿真和實驗研究的基礎上，采用定量與定性相結合的方法，對現有基于模型的占空比方法進行深度解析，提出一個簡單易實現并且對參數變化魯棒性強的新占空比確定方法，考慮了對轉矩和磁鏈誤差的同時優化。該新型占空比確定方法的原理如下。

在給出新的占空比確定方法之前，先來分析一下式（14）的占空比確定方法，重寫為

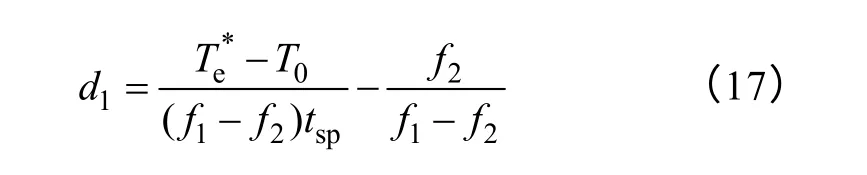
由式（17）可知，第一項正比于轉矩誤差，第二項正比于轉矩的下降斜率f2。為了消除參數依賴性，不妨假定分母(f1-f2)tsp是常數，然而，式（17）中與f2相關的第二項仍然很復雜，正如式（9）所示，并且仍依賴電機參數。注意到轉矩的下降斜率f2是由零電壓矢量引起的，而零矢量一般會導致定子磁鏈幅值的降低，為此可以認為第二項與磁鏈誤差成正比。考慮占空比的非負性，最終得到一種新型占空比確定方法，具體表達式為

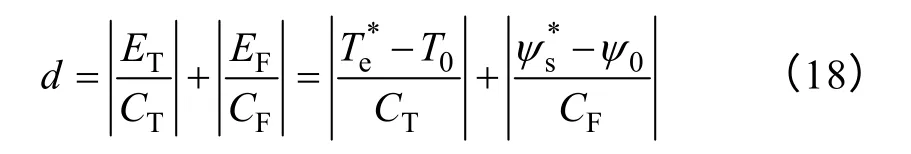
式中 Te*，ψs*——轉矩和定子磁鏈的參考值；

ψ0——第k 個采樣時刻的定子磁鏈值；

CT，CF——正的常數。

通過使用固定的常數CT和CF，希望新占空比確定方法受到轉矩斜率計算的影響更小。對于 CT和CF的調制應綜合考慮轉矩動態響應和穩態性能的影響，在進行大量仿真和實驗研究的基礎上發現，半額定的轉矩值和恒定的定子磁鏈值效果比較理想。一旦調整好，CT和CF便是兩個固定的常數。進一步研究發現，常數CT和CF的選擇對系統性能的影響也不是很大。

需要指出的是，由于新占空比方法僅改變所選有效電壓矢量的作用時間，而該有效電壓矢量來自傳統的DTC 矢量表。極端情況下占空比為1，此時則蛻化為普通的矢量表DTC。而在其他情況下，即使是在穩態運行時，磁鏈和轉矩的瞬時誤差也不大可能同時為0，式（18）采取的兩個絕對值運算符保證了占空比大于0。因此，系統的穩定性不受影響。這也解釋了為什么存在不同的占空比確定方法。它們的區別僅在于穩態脈動有所不同，但都可以保證系統的穩定性。

4.3 新占空比方法分析

與之前的占空比控制方法相比，簡單性是本方法的第一個優點，可以看出式（18）比式（14）～式（16）更簡單。第二個優點是對電機參數的變化魯棒性更強。對于先前方法式（14）～式（16），由式（8）和式（9）計算的轉矩斜率被用來確定占空比，它需要知道定子電阻、定子電感、轉子電感和定轉子互感等信息。而本文所提的新型占空比控制方法不需要額外的電機參數，因此受到電機參數變化的影響更小。

5 定子磁鏈估計

在DTC 中通常使用電壓模型估計定子磁鏈，在低速時定子電壓值較小，若定子電阻值不準確，定子電阻壓降的偏差對積分結果的影響會增大。本文使用基于全階觀測器的方法估計定子磁鏈，可以在全速域范圍內準確的觀測磁鏈。

由式（1）～式（4）式得到使用定子電流矢量和定子磁鏈矢量為狀態變量的異步電機模型為

根據式（19）可以構造出異步電機的全階觀測器模型

由于電機是穩定的物理系統，因此通常選擇G使得觀測器的極點正比于電機的極點[20,21]，以保證觀測器的穩定收斂，且一般k＞1 以保證觀測器的誤差收斂速度。需要注意的是，觀測器極點與電機極點的比值k 越大則觀測器收斂速度越快，但相應的抗干擾能力下降，因此k 值的選擇一般是快速性和抗干擾性的折衷。增益矩陣G 的一般形式為

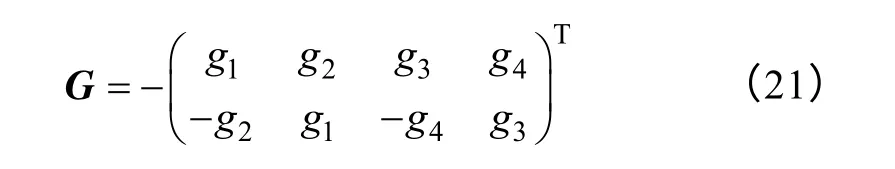
本文采用文獻[20]的方法，解析推導得到矩陣G 各個元素的表達式為

6 各種占空比確定方法的仿真比較

到目前為止針對異步電機還沒有文獻對各種占空比確定方法進行過比較研究，為此本文首先在Matlab/Simulink 中對已有經典方法和本文所提新方法進行仿真比較研究，以考察所提新占空比確定方法的性能。控制系統在1 050r/min 運行，采樣頻率為10kHz，系統的外環使用PI 速度控制器產生轉矩參考值。轉矩和磁鏈滯環比較器的寬度均設為零，其輸出僅表明轉矩和磁鏈誤差的正負。基于新占空比控制的DTC 控制系統框圖如圖3 所示，異步電機和控制系統參數見下表。

圖3 新的基于占空比控制的DTC 控制系統框圖 Fig.3 Basic block diagram of the proposed DTC system with duty-ratio control

表 異步電機和控制系統參數 Tab. Induction motor and system parameters

在“占空比控制”模塊中，所選有效電壓矢量的占空比由式（14）～式（16）和式（18）計算出。一旦得到占空比d，在此采樣周期的前d 部分時間應用所選有效電壓矢量，剩余的時間則應用零電壓矢量。為了減小開關損耗，當選出的有效電壓矢量是V1（100）、V3（010）和V5（001）時，緊隨其后的零電壓矢量為V0（000），其他情況下為V7（111）。另外需要注意的是，當轉矩不處于穩態時，由式（14）～式（16）計算出的d 值可能超出0～1 的范圍。當d＞1 時，令d=1；當d＜0 時，令d=0。

圖4 給出了異步電機從靜止起動到1 050r/min和0.3s 時突加7N·m 負載時的仿真波形，包括傳統DTC 和各種基于占空比控制的DTC。圖中從上到下的曲線依次是有效電壓矢量的占空比、定子磁鏈和電磁轉矩。各種方法中轉矩無論是在起動時刻還是在負載轉矩突變時刻，都表現出相同迅速的轉矩動態響應。其中，在穩態運行時傳統DTC 方法的轉矩脈動最大，幾乎達到了6N·m，其次是直接平均轉矩控制方法，大約為4N·m，最小轉矩脈動DTC 方法比無差拍DTC 方法的轉矩脈動要小，但效果不是很明顯，轉矩脈動都在近似3N·m 左右，而其占空比的計算式要比無差拍方法復雜得多，三種經典占空比確定DTC 方法的磁鏈脈動與傳統DTC 方法沒有明顯的差別，因為它們在占空比的確定中都沒有考慮對磁鏈的控制。本文所提的新方法同時減小了轉矩和磁鏈脈動，轉矩脈動大約為2N·m，并且通過對零電壓矢量的合理選擇減小了開關損耗。

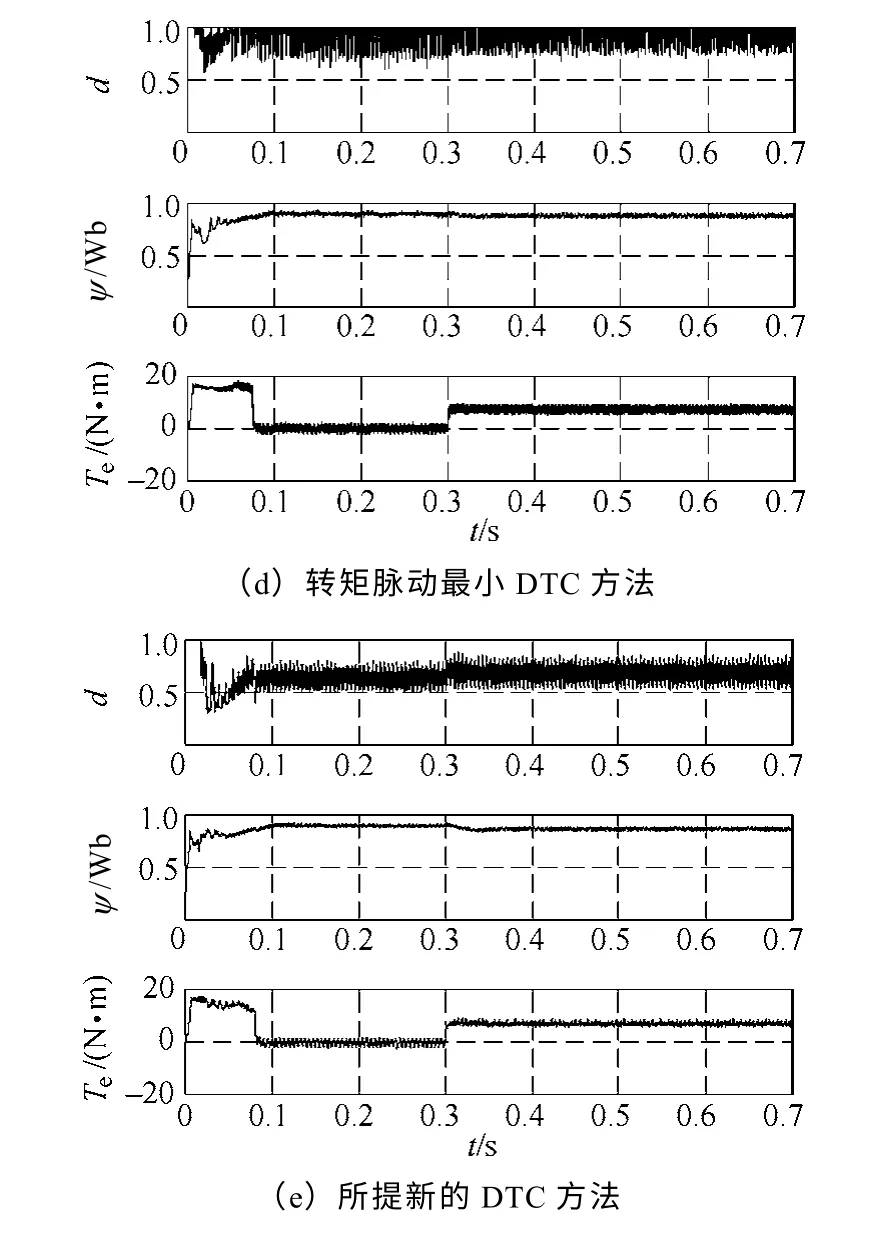
圖4 各種占空比控制方法與傳統DTC 方法的比較 Fig.4 Comparative study of various duty ratio control methods with conventional DTC

7 實驗結果

為了進一步驗證本文所提新占空比控制 DTC方法的可行性，在兩電平逆變器饋電的異步電機驅動系統中進行了實驗。為了獲得較好的比較效果，實驗中傳統DTC 方法采樣頻率使用20kHz，而新方法使用的采樣頻率為10kHz。控制器采用32 位浮點DSP（TMS320F28335），可以方便地實現本文的控制算法。另外控制板上還擴展了4 通道的D-A，用于內部變量觀測。實驗中除電流采用電流探頭直接測得外，其他變量都是通過12 位D-A 輸出到泰克示波器上顯示。異步電機和控制系統參數與表1 中所列相同。

首先研究系統在不同轉速時的穩態性能。圖5給出了傳統DTC 和本文所提新方法在10%額定轉速和100%額定轉速滿載時的穩態響應波形。圖中曲線從上到下依次為電機轉速、電磁轉矩、定子磁鏈和定子電流。可以看出，不論是在高速還是在低速時，基于新型占空比控制的DTC 相比傳統DTC的轉矩脈動都有明顯減小，而磁鏈脈動雖有減小，但效果不如仿真明顯，基本證實了本文所提方法的有效性。

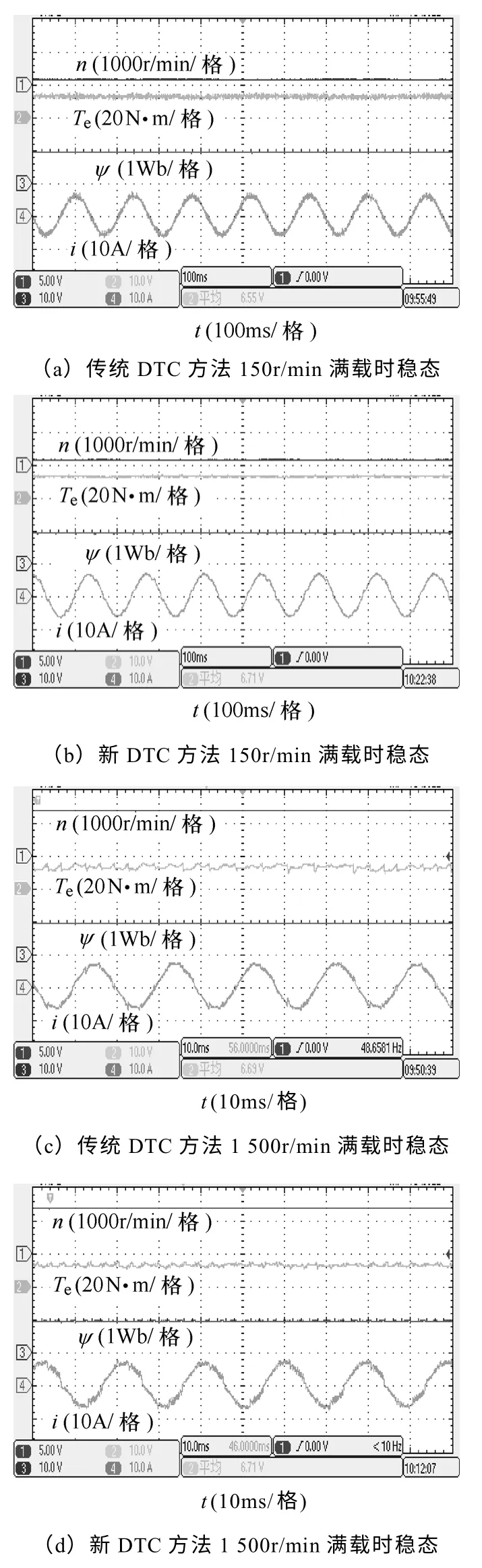
圖5 新占空比控制方法與傳統DTC 方法穩態波形 Fig.5 Steady-state waveforms of the new duty ratio control and conventional DTC method

圖6 給出了傳統DTC 和新方法在空載時從靜止到1 500r/min 的起動波形，通過對PI 速度控制器進行限幅，電機很快達到額定轉速。比較發現兩者的動態響應過程沒有明顯差別，從而證明新方法保持了傳統DTC 方法動態響應迅速的優點。

圖6 新占空比控制方法與傳統DTC 方法起動波形 Fig.6 Starting waveforms of the new duty ratio control and conventional DTC method

圖7 給出了傳統DTC 和所提新方法在額定轉速運行時突加減負載的波形，對比發現，新方法同樣表現出很強的抗干擾能力，動靜態性能十分良好。

圖7 新占空比方法與傳統DTC 方法突加減負載波形 Fig.7 Step and subtract load waveforms of the new duty ratio control and conventional DTC method

8 結論

本文針對異步電機，在比較研究三種經典占空比控制方法性能的基礎上，提出了一種對轉矩和磁鏈誤差進行同時優化的占空比控制方法。為了進一步改善系統性能，使用基于全階觀測器的方法估計定子磁鏈，可以在全速域范圍內準確的觀測磁鏈。仿真和實驗結果表明，這種在占空比控制中對轉矩和磁鏈誤差同時進行優化的新型DTC 策略不但能夠有效地減小傳統DTC 的轉矩和磁鏈脈動，而且保持了傳統DTC 響應迅速、控制簡單的優點，改善了傳統DTC 的控制性能。

[1] Casadei D,Profumo F,Serra G,et al.FOC and DTC:two viable schemes for induction motors torque control[J].IEEE Transactions on Power Electronics,2002,17(5):779-787.

[2] Takahashi I,Noguchi T.A new quick-response and high-efficiency control strategy of an induction motor[J].IEEE Transactions on Industry Applications,1986,22(5):820-827.

[3] Depenbrock M.Direct self-control(DSC) of inverter- fed induction machine[J].IEEE Transactions on Power Electronics,1988,3(4):420-429.

[4] Buja G S,Kazmierkowski M P.Direct torque control of PWM inverter-fed AC motors—a survey[J].IEEE Transactions on Industrial Electronics,2004,51(4):744-757.

[5] Tiitinen P,Surandra M.The next generation motor control method,DTC direct torque control[C].Proc of Int Conf Power Electron,Drives and Energy Syst for Ind Growth,New Delhi,India,1996:37-43.

[6] Lai Yenshin,Chen Jianho.A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction [J].IEEE Transactions on Energy Convers,2001,16(3):220-227.

[7] Lascu C,Trzynadlowski A.Combining the principles of sliding mode,direct torque control,and space- vector modulation in a high performance sensorless ac drive[J].IEEE Transactions on Industry Applications,2004,40(1):170-177.

[8] Habetler T G,Profumo F,Pastorelli M et al.Direct torque control of induction machines using space vector modulation[J].IEEE Transactions on Industry Applications,1992,28(5):1045-1053.

[9] Kenny B,Lorenz R.Stator- and rotor-flux- based deadbeat direct torque control of induction machines [J].IEEE Transactions on Industry Applications,2003,39(4):1093-1101.

[10] Zhang Yongchang,Zhu Jianguo.Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J].IEEE Transactions on Power Electronics,2011,26(1):235-248.

[11] Flach E,Hoffmann R,Mutschler P.Direct mean torque control of an induction motor[C].Proc European Power Electronics and Applications(EPE),Trondheim,Norway,1997:672-677.

[12] Kang J K,Sul S K.New direct torque control of induction motor for minimum torque ripple and constant switching frequency[J].IEEE Transactions on Industry Applications,1999,35(5):1076-1082.

[13] 楊家強,黃進.異步電動機直接轉矩控制轉矩脈動最小化方法研究[J].電工技術學報,2004,19(9):23-29.

Yang Jiaqiang,Huang Jin.Research on torque ripple minimization strategy for direct torque control of induction motors[J].Transactions of China Electrotech- nical Society,2004,19(9):23-29.

[14] Romeral L,Arias A,Aldabas E,et al.Novel direct torque control(DTC) scheme with fuzzy adaptive torque- ripple reduction[J].IEEE Transactions on Industrial Electronics,2003,50(3):487-492.

[15] 劉軍,劉丁,吳浦升,等.基于模糊控制調節電壓矢量作用時間策略的永磁同步電機直接轉矩控制仿真研究[J].中國電機工程學報,2004,24(10):148-152.

Liu Jun,Liu Ding,Wu Pusheng,et al.The simulation analysis of permanent magnet synchronous motor based on the strategy of modulating the time of voltage vector[J].Proceedings of the CSEE,2004,24(10):148-152.

[16] Kouro S,Cortes P,Vargas R,et al.Model predictive control—a simple and powerful method to control power converters[J].IEEE Transactions on Industrial Electronics,2009,56(6):1826-1838.

[17] Geyer T,Papafotiou G,Morari M.Model predictive direct torque control part I:concept,algorithm,and analysis[J].IEEE Transactions on Industrial Electronics,2009,56(6):1894-1905.

[18] Drobnic K,Nemec M,Nedeljkovic D,et al.Predictive direct control applied to AC drives and active power filter[J].IEEE Transactions on Industrial Electronics,2009,56(6):1884-1893.

[19] Miranda H,Cortes P,Yuz J,et al.Predictive torque control of induction machines based on state-space models[J].IEEE Transactions on Industrial Electronics,2009,56(6):1916-1924.

[20] Kubota H,Matsuse K,Nakmo T.DSP-based speed adaptive flux observer of induction motor[J].IEEE Transactions on Industry Applications,1993,29(2):344-348.

[21] Yang G,Chin T H.Adaptive-speed identification scheme for a vector-controlled speed sensorless inverter- induction motor drive[J].IEEE Transactions on Industry Applications,1993,29(4):820-825.

[22] Jehudi M,Jan A M.Speed-sensorless direct torque control of induction motors using an adaptive flux observer[J].IEEE Transactions on Industry Applica- tions,2000,36(3):778-785.