一種新的混合矢量磁滯模型磁滯算子定義方法

李丹丹 劉福貴 李永建 趙志剛 楊慶新,

（1.河北工業大學河北省電磁場與電器可靠性省部共建重點實驗室 天津 300130 2.天津工業大學天津市電工電能新技術重點實驗室 天津 300387）

1 引言

對鐵心材料磁特性進行精確建模是提高電機工作性能和運行效率并降低能耗的重要途徑，也是國際電工領域的前沿和熱點問題，但由于問題本身的復雜性，這一領域一直處于發展階段。到目前為止，各國學者已經提出了多種模型用來模擬材料的磁滯現象，主要提出了兩類磁滯模型，一類是純數學模型（例如Preisach 模型[1]和Hodgdon 模型[2]），另一類是物理模型（例如Stoner-Wohlfarth（S-W）模型[3]和Jiles-Atherton（J-A）模型[4]）。由于電磁裝置運行中磁心特性多呈矢量磁特性，而經典基礎模型大都是標量模型，不能精確模擬磁材料在工程應用中的磁特性，為此學者們使用各種方法把經典標量模型擴展到矢量范疇，如Mayergoyz 模型[5]和Coupled Hysterons 模型[6]等。經典S-W 模型適用于橢球形、單疇、單軸磁性粒子矢量磁特性模擬，在這些限定條件下可描述多種磁特性。Mayergoyz 模型用各個方向上磁化強度的連續分量的矢量和計算總磁化強度，該模型比S-W 模型更具普遍性，但不能精確模擬旋轉外加場下的磁特性。Coupled Hysterons 模型對于具有橢球形粒子的磁材料能準確描述其飽和特性和損耗特性，但在建模時需要根據磁化過程進行旋轉和定位修正。

近十幾年結合兩種或多種經典模型的混合磁滯模型逐漸成為磁滯模型的發展趨勢。從20 世紀90 年代開始，學者們就試圖用標量Preisach 模型與矢量S-W 模型相結合的方法對材料磁特性進行模擬[7,8]。2006 年Della Torre 等人提出了一般矢量磁滯模型（后被稱為DPC 模型）[9,10]，后續又提出了Preisach-Stoner- Wohlfarth（PSW）模型[11]，混合磁滯模型的發展步入系統化階段。PSW 模型使用外加磁場與粒子間的相互影響場的矢量和定義了一個網絡場，利用網絡場確定磁化方向和磁化強度幅值[12-15]；而DPC 模型的磁化方向和磁化強度幅值是分別由S-W 模型和Preisach 模型確定的[16-20]。這兩種模型都是通過結合Preisach 模型和S-W 模型進行建模的，統稱為混合矢量磁滯模型（Hybrid Vector Hysteresis Model，HVHM），拓寬了經典模型的適用范圍，結合了二者的優點，更精確的模擬磁材料矢量磁滯特性。

HVHM 的建模基礎是定義矢量磁滯算子，模型將磁滯算子定義為H 面內的一個由封閉的臨界面包圍的區域，每個磁滯算子有一個特定的臨界面。不同的材料具有臨界面的形狀不同，二維情況下，各向異性材料的臨界面為橢圓形（PSW 模型），長軸為難磁化軸，短軸為易軸；各向同性材料的臨界面為圓形（RVM 模型[13]）。每個磁滯算子正則化處理后的磁化強度具有單位幅值，當對其施加外場時，磁化強度大小不變，方向隨外場變化發生轉動。

根據HVHM 的建模思想，從能量角度出發，利用S-W 建模原理分析了磁性粒子處于磁化穩定狀態的條件，借助于磁性粒子產生的矢量場的等勢線方程，分別給出了各向異性和各向同性材料磁滯算子的臨界線方程，將混合矢量磁滯模型中的磁滯算子定義為由等勢線包圍的封閉區域，具有單位磁化強度，磁化方向可以隨外場方向變化發生轉動。假定外場在磁滯算子臨界線內部時對磁化方向沒有影響，當外場在臨界面內部時，磁化方向與磁滯算子原磁化方向相同，直到外場穿出臨界面，磁化方向發生巴克豪森躍變，轉到由外場決定的磁化方向上，總磁化強度等于所有磁滯算子磁化強度的矢量和。

2 磁性粒子及等勢線

考慮由單疇單軸各向異性的磁性材料組成的橢球形磁性粒子，假定粒子沿各向異性軸磁化到飽和狀態，可以用磁化強度M 來描述其磁化狀態，也可以用單位矢量m=M/MS描述。粒子所具有的特性由單軸各向異性能和外場能-μ0M·Ha控制，定義各向異性軸為易軸（x 軸為易軸），零外場時，磁化強度與易軸同向，施加外場后，磁化強度由易軸方向向外場方向轉動。磁化強度、外場和易軸的關系如圖1 所示。

圖1 外場Ha、磁化強度M 與易軸間的關系 Fig.1 The relations between applied field Ha ,magnetization vector M and easy axis

磁性粒子的總自由能等于單軸各向異性能加外場能[3]，表達式如式（1）所示。

式中，V 為磁性粒子的體積；K 為粒子各向異性常數；θ 和θH分別為磁化強度M、外場Ha與易軸間的夾角。該方程具有一個狀態變量θ，兩個控制變量θH和Ha。

為了方便計算，給出簡化方程

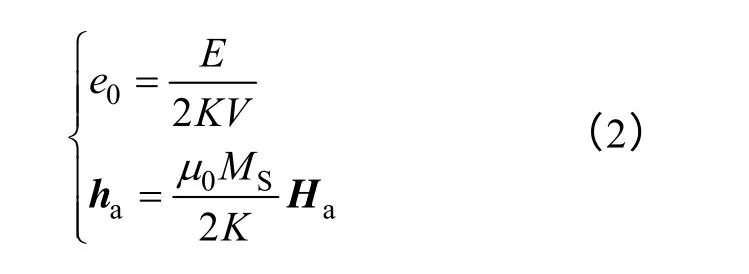
式中，e0為簡化后的總能量。

使用式（2）對式（1）進行簡化處理，并用ha沿坐標軸的兩個分量hx和hy表示外加磁場，式（1）可以改寫為式（3）。

磁化穩定狀態發生在自由能取最小值的時候，即能量方程滿足能量取最小值條件，計算式（3）的一階導數并強加條件?e0/?θ =0 得能量方程取最小值的條件如式（4）所示。

結合式（3）和式（4），分別用hx和hy表示外場代入能量方程，由de0=0 得單個磁性粒子產生的矢量場的等勢線方程為

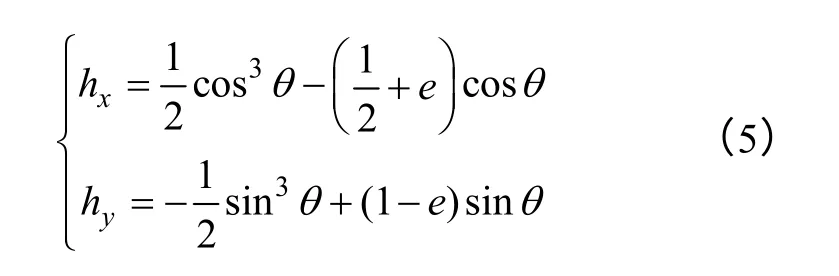
式中，e 為等勢線上的能量的固定值。

由于沿等勢線的能量變化量恒等于零，當外場沿等勢線變化 dha時相對應粒子自由能的變化量deeq= -μ0m·dha= 0，所以當外場沿等勢線變化時，粒子的磁化方向垂直于等勢線。磁力線是外場平面內所有參考點上磁化強度的切線，因此磁力線垂直于等勢面。

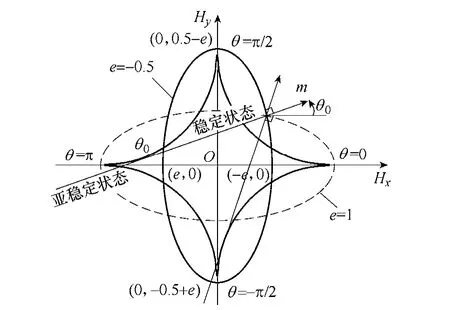
圖2 S-W 模型星形判定法則示意圖（橢圓型曲線為 等勢線，其中實曲線e = -0.5，虛曲線e = 1） Fig.2 The diagram for asteroid rule of the S-W model (The elliptical curve is the equipotential curves,the solid curve:e = -0.5,the dotted curve:e = 1)

圖2 中的星形線是粒子能量方程取最大值或最小值的臨界曲線，S-W 模型星形判定法則表明[3]，H 面內某點的磁化方向為星形線的切線方向，然后根據該點與星形線的位置關系確定磁化穩定狀態下的磁化方向。由星形判定法則和磁力線垂直于等勢面（如圖2 所示）可得，e＞1 時等勢線上的點都處于亞穩定狀態；-0.5＜e＜1 時與橫軸相交的等勢線上的點都處于穩定狀態，與縱軸相交的等勢線上的點都處于亞穩定狀態；e＜-0.5 時等勢線上的點都處于穩定狀態。

3 磁滯算子定義

在HVHM 中磁滯算子的定義是非常重要的，對各向異性材料，每條主軸的磁特性均不同，只有一條主軸為易軸。本文選用處于平衡狀態的等勢線方程，即式（5）中的參數e 取值范圍為e＜-0.5，作為磁滯算子臨界面方程，每個磁滯算子都是由一個特定的等勢線包圍的區域，具有單位磁化強度，臨界面上每一點上的磁化方向沿該點的外法線方向。根據混合矢量磁滯模型建模原理，假定當外場進入臨界面時，磁化方向被固定在穿入點時的磁化方向上，直到外場穿出臨界面時，磁化方向發生巴克豪森躍變，突變到臨界面的法線方向上。

圖3 給出了不同θH下的磁滯算子在兩個坐標軸上的磁滯回線Mx-Hx和My-Hy。外場取不同方向時，算子磁化強度在坐標軸上的兩個分量的開關閾值不同；外場與短軸夾角越小，磁滯損耗越小，越容易磁化；外場與長軸夾角越小，磁滯損耗越大，越難被磁化，即短軸為磁滯算子的易磁化軸，長軸為難磁化軸。選用等勢線方程作為各向異性材料的磁滯算子臨界面方程。

圖3 不同θH 下磁滯算子在x-和y-軸方向上的磁滯回線 Fig.3 Hysteresis loops of x- and y-component of magnetization for alternate magnetizations with different θH

對于各向同性材料，不存在各向異性能，粒子性能由外場能控制，表示為

粒子產生的等勢線方程為

等勢線是半徑為-e 的圓形，用等勢線方程定義各向同性材料磁滯算子臨界面方程，磁滯算子是由一個個半徑不等的圓形包圍的圓形區域，當外場沿等勢線變化時，粒子的磁化方向垂直于臨界面，臨界面是圓形的，磁化方向沿從圓心指向參考點的徑向方向，和RVM 模型相同[13]。

4 磁化過程分析

4.1 交變磁化

對磁滯算子施加交變磁化場，計算其磁化過程，這里只給出了各向異性材料磁滯算子的磁化過程。如圖4 所示，當外加磁場沿圖中所給磁化路徑A-B-A變化時，磁滯算子被交變磁化，磁化強度沿坐標軸的兩個分量與外場兩個分量之間的關系曲線如圖5所示。可以看到，當外場穿入臨界面后，磁化強度方向保持不變，直到外場穿出臨界面，磁化強度方向發生突變，轉到穿出點的法線方向上。單個磁性粒子的飽和磁化矢量m 的絕對值為1。

圖4 單個磁滯算子及交變磁化路徑A-B-A Fig.4 A hysteron with a magnetic path A-B-A

圖5 外場沿A-B-A 變化時磁滯算子的磁化回線 Fig.5 The corresponding Hysteresis loop

為了使模型更具一般性，考慮多個相互影響磁滯算子，如圖6 所示，給出了三個考慮了相互影響場影響的磁滯算子和兩個不同方向的交變磁化路徑。考慮粒子間相互影響場時，粒子所面臨的總磁場等于外場與影響場的矢量和，可以表示為

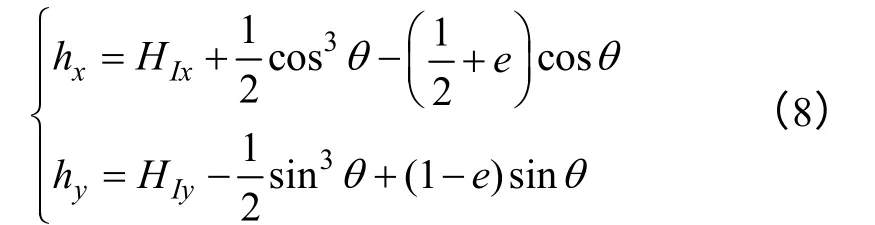
圖6 三個磁滯算子及兩個不同的交變磁化路徑 Fig.6 Three hysterons with two different magnetic paths

為了方便計算，將磁滯算子中心從原點做一個矢量位移，移到（HIx,HIy）處，這樣臨界面方程和不考慮影響場的相同，只是中心位置發生了變動，如圖6 所示。總磁化強度沿坐標軸的分量分別等于所有磁滯算子的磁化強度沿坐標軸分量的矢量和。當外加磁場沿圖 6 所示的磁化路徑 A1-B1-A1與A2-B2-A2變化時，磁化強度分量與外場分量之間的關系曲線如圖7 與圖8 所示。由圖7、圖8 可以看到，外場與磁滯算子相交時發生巴克豪森躍變，產生磁滯損耗。

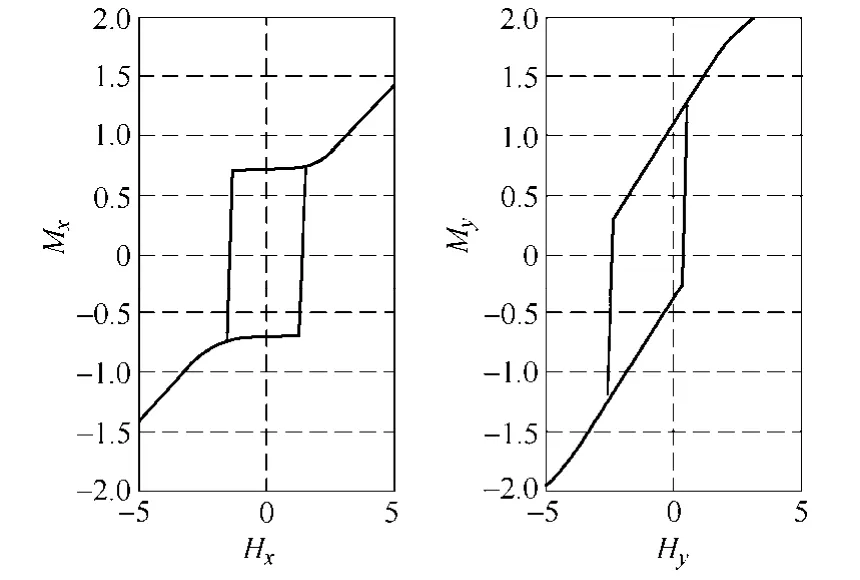
圖7 沿A1-B1-A1 的磁化回線 Fig.7 The magnetic loops correspond to path A1-B1-A1

圖8 沿A2-B2-A2 的磁化回線 Fig.8 The magnetic loops correspond to path A2-B2-A2

4.2 旋轉磁化

在旋轉激磁條件下，可分析各向異性材料磁滯算子的旋轉磁化特性。如圖9 所示，當外場分別沿逆時針方向變化的圓形磁化路徑C、D、E 對磁滯算子進行旋轉磁化時，磁化強度分量與外場分量之間的關系曲線如圖10 所示。由圖10 所示的磁化曲線可以看到，當磁化路徑與磁滯算子相交時，會產生磁滯。圖9 中磁化路徑C、D 都與磁滯算子有相交部分，與之相對應的磁化曲線具有明顯的磁滯現象，即只要磁化路徑穿出磁滯算子臨界面，就會發生巴克豪森躍變，產生磁滯損耗；而對于圖9 所給出的三個磁滯算子來說，沿磁化路徑E 變化的外場足夠大，磁化方向與外場方向相同，計算所得的磁化回線與所施加外場的回線形狀相同，沒有磁滯損耗。

圖9 三個分別從C、D、E 開始的 逆時針變化圓形磁化路徑 Fig.9 Three different counterclockwise circulars applied magnetic field paths:starting from C、D、E

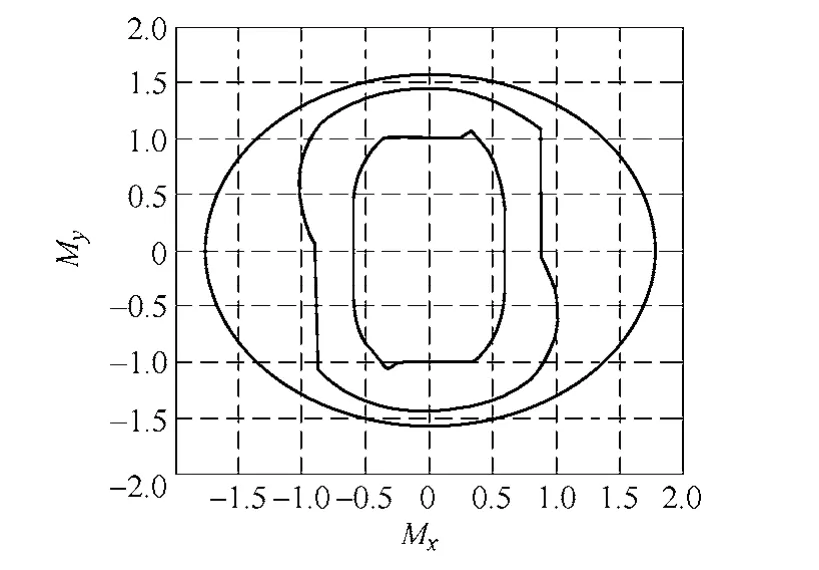
圖10 對應的磁化回線 Fig.10 The corresponding hysteresis loops

5 磁滯算子特性分析

5.1 損耗特性

由磁滯算子臨界面方程可得，當θ = 0°或180°時，磁滯算子的臨界面與x 軸上的交點為hx= -e 和hx= e；當θ = 90°或-90°時，磁滯算子的臨界面與y 軸的交點為hy=0.5-e 和hy=-(0.5-e)，如圖2 所示。磁滯算子的臨界面的x 軸截距與y 軸截距之間的關系可以表示為

則磁滯算子的臨界面的軸長比為

隨外場增大，A 逐漸趨向于1，磁滯算子的臨界面近似為圓形，說明當外場足夠大時，各向異性材料的磁化特性和各向同性材料相近，磁化方向近似與外場方向相同。

在旋轉外場下，當外加磁場足夠大時，磁滯算子完全包含在激磁場中，臨界面與外場沒有相交部分，磁化方向與外場方向相同，不產生磁滯損耗，模型具有損耗特性。

5.2 熱力學第二定律

混合矢量磁滯模型中磁滯算子的能量變化要滿足熱力學第二定律：任意一個與磁滯算子臨界面相交的封閉路徑必定存在能量損耗[19]。也就是說，磁滯算子沿任意一個穿過臨界面的封閉磁化路徑的能量變化必須小于等于零。如圖11 給出了一個磁滯算子和一條任意封閉的磁化路徑γ，P1、P2分別為γ與臨界面的兩個交點，P1為穿入點，P2為穿出點。磁滯算子的臨界面是一條等勢線，且當外場穿入臨界面時不發生能量損耗，因此磁滯算子外部的任意一條連接穿入點P1和穿出點P2的磁化路徑γ-out 的能量變化為Eγ-out=0。而當外場在磁滯算子內部時，外場對強化強度沒有影響，磁化方向被固定在穿入點P1處的磁化方向上，不產生能量變化，直到外場 穿出臨界面時，磁化方向在穿出點P2處發生巴克豪森躍變，產生能量損耗，因此，沿臨界面內部任意一條從P1點到P2點的磁化路徑γ-in 的能量變化為Eγ-in＜0。封閉磁化路徑γ 的能量變化為Eγ= Eγ-out+ Eγ-in＜0，磁滯算子的能量變化滿足熱力學第二定律。

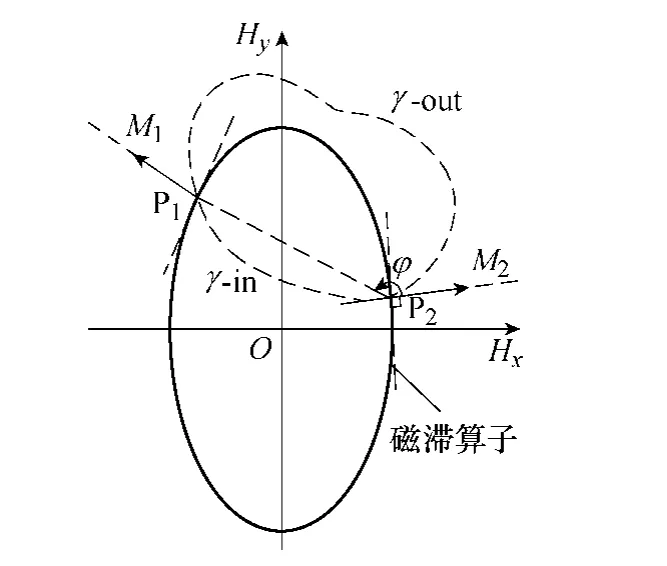
圖11 二維矢量磁滯算子滿足熱力學第二定律 Fig.11 The congruence of the 2D hysteron with the second principle of the thermodynamics

5.3 擦除特性

模型的磁化過程與磁化路徑及其在臨界面上的穿入穿出點有關，具有磁化歷史擦除特性。如圖12所示，沿從原點到P1點的磁化路徑α 對磁滯算子磁化，P1點的磁化強度取決于路徑α 穿入臨界面的穿入點；沿從P1點到P2點的磁化路徑β1繼續對磁滯算子進行磁化，由于P1點、P2點及路徑β1都是在磁滯算子內部，所以P2點的磁化強度依舊依賴于路徑α；沿從P2點到P3點的磁化路徑β1繼續對磁滯算子進行磁化，路徑β2與臨界面有穿出點，P3的磁化強度不再取決于路徑α，而是取決于路徑β2的穿出點，路徑α 產生的磁化效果已被路徑β2擦除。

圖12 二維矢量磁滯算子擦除特性 Fig.12 The deletion property of the 2D hysteron

若沿路徑α 對磁滯算子磁化之后，再沿穿過P1點的封閉路徑β3繼續對磁滯算子磁化，P1點的磁化強度只取決于路徑β3的穿入點，與路徑α 無關，路徑α 產生的磁化效果已經被新的路徑β3擦除。

單個磁滯算子具有擦除特性，但不具備 Man- delung 定則[21]中的返回點記憶特性，只有同時考慮多個磁滯算子的磁化過程時，模型才符合描述磁滯特性的Mandelung 定則。

6 總結

從能量角度出發，提出了HVHM 模型中二維矢量磁滯算子一種定義方法，分別給出了各向異性和各向同性材料磁滯算子的臨界面方程，結合S-W 模型星形判定法則，確定了外場在磁滯算子臨界面外部時磁化方向沿臨界面法線方向，外場在臨界面內部時磁化方向被固定在穿入點處的磁化方向上。

計算分析了在交變磁化場和旋轉磁化場中磁滯算子的磁化過程，當外場與磁滯算子相交時，產生磁滯損耗，當外場值足夠大時，磁化方向與外場同向，沒有磁滯損耗。對磁滯算子的特性分析表明，磁滯算子滿足熱力學第二定律，具有損耗和擦除特性，滿足描述磁滯特性的Mandelung 定則。該定義方法有助于精確模擬磁化過程、提高矢量磁滯模型的有效性和可靠性，為提高變壓器、電機等電工裝置運行效率并降低能耗奠定了理論基礎。

[1] Preisach F.über die magnetische nachwirkung[J].Zeitschrift Für Physik,1935,94(5-6):277-302.

[2] Coleman B D,Hodgdon M L.A constitutive relation for rate-independent hysteresis in ferro-magnetically soft materials[J].International Journal of Engineering Science,1986,24(6):897-919.

[3] Stoner E C,Wohlfarth E P.A mechanism of magnetic hysteresis in heterogeneous alloys[J].IEEE Transactions on Magnetics,1991,27(4):3475-3518.

[4] Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Magnetism and Magnetic Materials,1986,61(1):48-60.

[5] Mayergoyz I D.Mathematical models of hysteresis [M].New York:Springer Verlag,1991.

[6] Della Torre E.Magnetic hysteresis[M].New York:IEEE Press,1999.

[7] Michelakis C,Litsardakis G,Samaras D.A contribu- tion to 2D vector preisach modelling[J].Journal of Magnetism and Magnetic Materials,1996,157:347- 348.

[8] Koh C S,Hahn S,Park G S.Vector hysteresis modeling by combining stoner-wohlfarth and preisach models [J].IEEE Transactions on Magnetics,2000,36(4):1254-1257.

[9] Della Torre E,Pinzaglia E,Cardelli E.Vector modeling- part I:Generalized hysteresis model[J].Physica B:Condensed Matter,2006,372(1):111-114.

[10] Della Torre E,Pinzaglia E,Cardelli E.Vector modeling- part II:ellipsoidal vector hysteresis model,numerical application to a 2D case[J].Physica B:Condensed Matter,2006,372(1):115-119.

[11] Della Torre E,Cardelli E.A preisach-stoner-wohlfarth vector model[J].IEEE Transactions on Magnetics,2006,42(10):3126-3128.

[12] Kahler G R,Della Torre E,Cardelli E.Implementation of the preisach-stoner-wohlfarth classical vector model [J].IEEE Transactions on Magnetics,2010,46(1):21-28.

[13] Cardelli E,Della Torre E,Pinzaglia E.Magnetic energy and radial vector model of hysteresis[J].Journal of Applied Physics,2006,99(8):08D703-08D703-3.

[14] Della Torre E,Cardelli E,Bennett L H.Identifying hysteresis losses in magnetic media[J].IEEE Transac- tions on Magnetics,2010,46(11):3844-3847.

[15] Della Torre E,Bennett L H,Jin Y.An effect of particle size on the behavior of ferromagnetic materials [J].Journal of Magnetism and Magnetic Materials,2012,324(14):2189-2192.

[16] Cardelli E,Della Torre E,Faba A.Properties of a class of vector hysteron models[J].Journal of Applied Physics,2008,103(7):07D927-07D927-3.

[17] Cardelli E,Della Torre E,Faba A.Analysis of a unit magnetic particle via the DPC model[J].IEEE Transac- tions on Magnetics,2009,45(11):5192-5195.

[18] Cardelli E,Della Torre E,Faba A.Numerical imple- mentation of the DPC model[J].IEEE Transactions on Magnetics,2009,45(3):1186-1189.

[19] Cardelli E.A general hysteresis operator for the mode- ling of vector fields[J].IEEE Transactions on Magnetics,2011,47(8):2056-2067.

[20] Cardelli E,Della Torre E,Faba A.A general vector hysteresis operator:Extension to the 3-D case[J].IEEE Transactions on Magnetics,2010,46(12):3990-4000.

[21] Mandelung E.On the magnetization by fast current and an operation principle of the magneto-detectors of rut herford-marconi[J].Ann Phys,1905,17:861-890.