魚雷發動機參數自整定PID控制

路　駿，韓勇軍，楊赪石，彭　博，萬榮華，韓新波，馬為峰

(中國船舶重工集團公司第七〇五研究所，陜西西安710075)

魚雷發動機參數自整定PID控制

路駿，韓勇軍，楊赪石，彭博，萬榮華，韓新波，馬為峰

(中國船舶重工集團公司第七〇五研究所，陜西西安710075)

摘要:提出一種用于魚雷發動機的參數自整定PID控制方法。該方法利用支持向量機的非線性函數擬合能力辨識發動機的動態特性，采用粒子群算法實現PID控制器的參數優化。仿真實驗表明，支持向量機能很好地擬合發動機的動態特性，基于粒子群算法的參數自整定PID控制器響應快速、無超調，控制效果良好，具有工程應用價值。

關鍵詞:魚雷發動機; PID控制;支持向量機;粒子群算法;參數優化

Self-tuning PID control scheme for torpedo engine

LU Jun，HAN Yong-jun，YANG Cheng-shi，PENG Bo，WAN Rong-hua，HAN Xin-bo，MA Wei-feng
(The 705 Research Institute of CSIC，Xi'an 710075，China)

Abstract:This paper presents a self－tuning PID control scheme for torpedo engine．Due to its excellent performance in nonlinear function approximation，support vector machine is used to identify the dynamics of torpedo engine．The PID parameters are tuned using particle swarm optimization．The simulation results demonstrate that the support vector machine is able to approximate engine dynamics with high accuracy，and the proposed controller achieves good performance in terms of convergence speed and overshoot．

Key words:torpedo engine; PID control; support vector machine (SVM) ; particle swarm optimization (PSO) ;parameter optimization

0　引言

PID控制具有算法簡單、魯棒性好、可靠性高等優點，因而被廣泛應用于系統控制領域。PID參數整定是影響PID控制效果的關鍵問題［1］。目前工程上PID參數的整定方法主要有臨界比例度法、衰減曲線法、Z－N法、快速整定法和繼電器法等。這些方法在實際應用中雖然可以不同程度地滿足要求，但由于PID控制器本身存在著靜態和動態之間、跟蹤設定值與抑制擾動之間、魯棒性與控制性之間等矛盾，使得PID參數整定依然是一個重要的研究課題。

近年來，越來越多的人工智能方法被應用于PID控制器設計和參數整定中［2］。如出現了基于神經網絡和遺傳算法的PID控制器參數整定與優化方法［3－4］。但神經網絡是基于經驗風險最小原則，存在著神經網絡結構和參數難以選擇、易陷于局部極值、過擬合等問題。

支持向量機［5］(support vector machines，SVM)是基于統計學習理論發展起來的一種新的分類和回歸工具，它通過結構風險最小化原理提高泛化能力，克服了神經網絡的上述缺陷，已被成功應用于模式識別和系統控制領域［6］。粒子群算法［7］(particle swarm optimization，PSO)是基于群體智能理論的優化算法，通過種群中粒子間的合作與競爭產生的群體智能指導優化搜索，具有算法簡單、收斂速度快、不容易陷入局部極值的優點，目前已廣泛應用于函數優化和模糊系統控制等領域［8］。結合二者的優點，本文提出一種基于支持向量機和粒子群算法的參數自整定PID控制器，并將其應用于魚雷發動機控制。仿真研究表明該方法具有滿意的控制效果。

1　控制器設計

基于支持向量機的參數自整定PID控制策略如

圖1所示。該控制策略利用作為發動機辨識模型的支持向量機產生預測信號，然后利用粒子群優化算法求解出最優PID參數，從而實現對發動機的預測控制。具體算法流程如下:

1)由控制要求獲取未來的期望輸出序列，即參考軌跡yr(k + 1) ;

2)預先測量得到發動機的開環輸入輸出數據，把它們作為訓練支持向量機的樣本，對支持向量機進行離線訓練，得到具有足夠精度的支持向量機模型;

3)利用支持向量機模型產生系統的預測輸出yp(k + 1) ;

4)將預測輸出與參考軌跡比較，計算未來時刻的期望誤差e(k + 1)。

5)通過粒子群算法極小化性能指標函數J(k)，獲得最優PID參數kp，ki，kd;

6)將控制量u(k + 1)作用于系統，返回1)。

圖1　基于SVM的參數自整定PID控制器框圖Fig.1 Scheme of self-tuning PID controller based on SVM

1.1支持向量機原理

用于系統辨識的支持向量機基本原理是:給定n組樣本數據{ (yk，xk) | k = 1，…，n}，其中xkRn是輸入樣本，ykR是輸出樣本，利用一個非線性映射Ф將數據從原空間映射到高維特征空間F，并在此空間構造最優線性回歸函數使其能夠很好的逼近給定數組［4］。由統計學習理論可知，該函數具有以下形式

在Vapnik ε不敏感損失函數的定義下

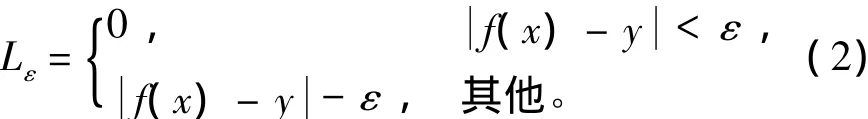
式(1)的求解轉化為下式的最優問題求解

式中:ε為回歸允許的最大誤差;ξi和ξi*為松弛變量，C為懲罰參數。

式(3)的求解可以轉化為Lagranage對偶問題求解

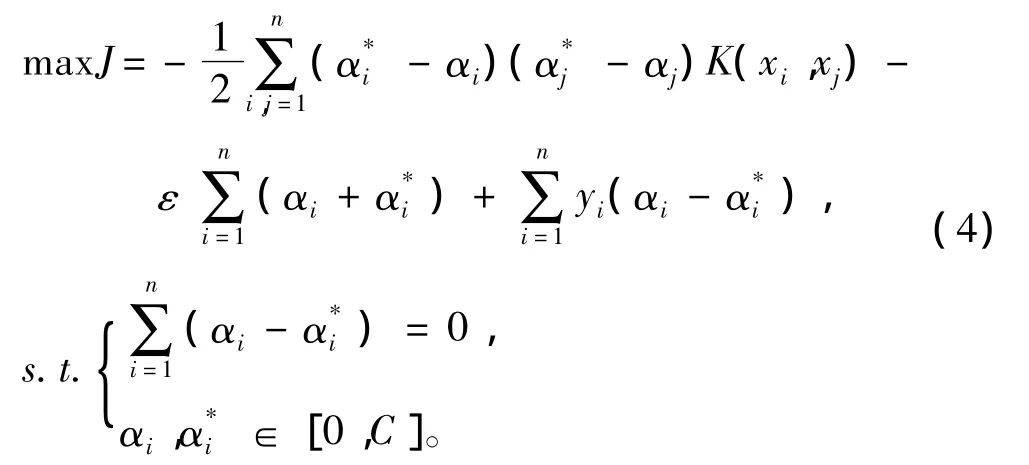
式中:аi和аi*定義為非負的Lagranage乘子，核函數定義為

發動機的工作過程往往具有高度的非線性，考慮用支持向量機來辨識其動態行為，離散系統k +1時刻的輸出可表示為:其中

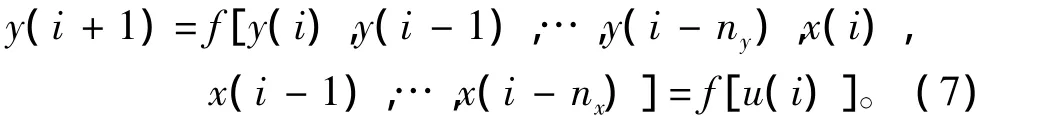
為建立支持向量機模型，首先構造訓練樣本［u(i)，y(i + 1)］。采用上述方法可將非線性的樣本數據映射為高維空間的線性輸出:

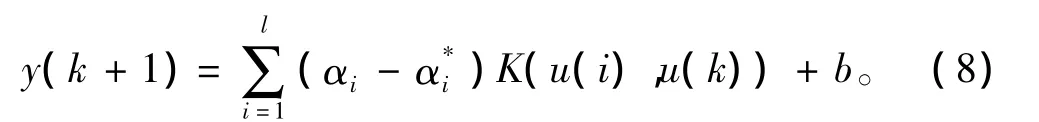
1.2PID參數整定

PID控制器的目標是產生控制信號u(k)能夠在k + 1時刻使系統輸出與參考模型輸出的差值最小。因此構造目標函數

其中μ為懲罰系數，誤差e定義為支持向量機模型預測的發動機輸出yp與參考模型輸出yr的差值

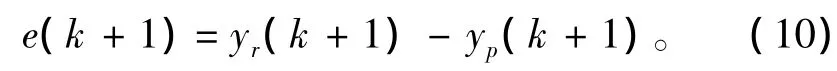
為改善控制過程的動態特性，引入參考軌跡。

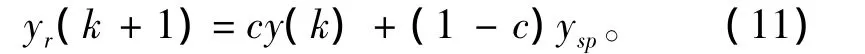
式中: y(k)為發動機實際輸出; ysp為發動機輸出的

目標值; c為可調參數(0＜c＜1)。

PID控制器參數整定問題則轉化為尋找最優解kp，ki，kd，使得上述目標函數取最小值。本文采用粒子群算法來求解這一優化問題。粒子群算法的基本原理如下:在D維的目標搜索空間中初始化一群隨機粒子，其中第i個粒子表示為一個D維向量Xi= (xi1，xi1，…，xiD)，i = 1，2，…，N，每個粒子的位置就是一個潛在的解。將Xi代入一個目標函數就可以算出其適應值，根據適應值的大小來衡量解的優劣。第i個粒子的速度也是D維向量，記為Vi= (vi1，vi1，…，viD)。第i個粒子迄今為止搜索到的最優位置稱為個體極值pbest，記作Pi= (pi1，pi1，…，piD)，整個粒子群迄今為止搜索到的最優位置稱為全局極值gbest，記作Pg= (pg1，pg1，…，pgD)。

PSO基于上述2個極值對粒子的速度和位置進行更新:

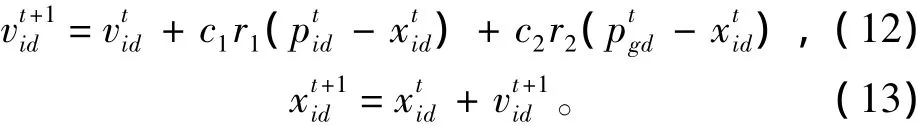
式中: i = 1，2，…，N，d = 1，2，…，D;學習因子c1和c2為非負常數; r1和r2為2個相互獨立的在區間［0，1］上均勻分布的偽隨機數。

粒子群算法流程如圖2所示。

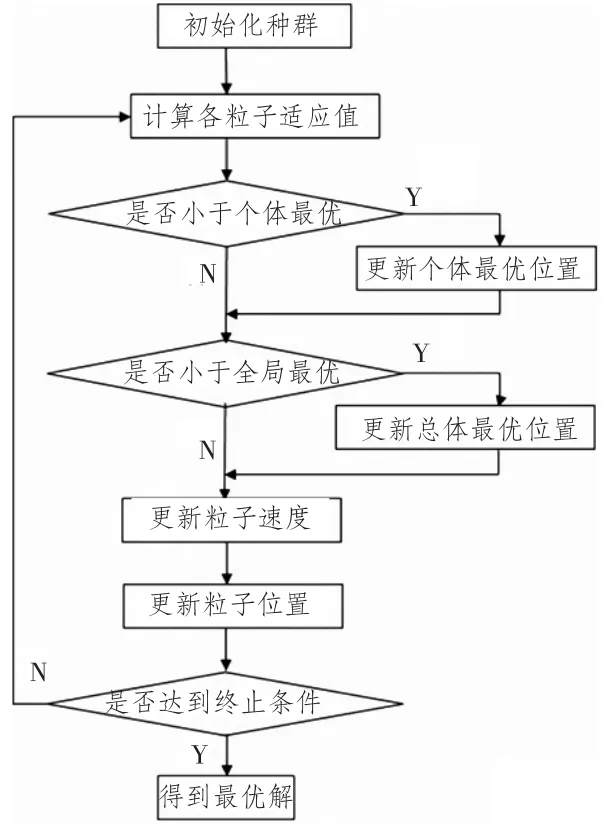
圖2　粒子群算法流程圖Fig.2　Flow chart of PSO algorithm

2　仿真研究

2.1發動機的辨識仿真

為了獲得發動機的辨識模型，必須收集發動機的輸入輸出數據，用以對支持向量機進行離線訓練。訓練中采用1 000組信號，前500組作為學習樣本用于訓練支持向量機，后500組用于測試所得支持向量機的性能。支持向量機的設計參數為: C = 10，000，ε= 0.01，σ= 40。

支持向量機辨識仿真結果如圖3和圖4所示，其中圖3為訓練樣本的擬合情況，圖4為測試樣本的擬合情況，圖中的數據作了無量綱化處理。由圖可知，支持向量機模型很好的擬合了訓練和測試樣本，表明支持向量機具有良好的辨識精度，經過訓練過支持向量機能夠準確描述發動機的動態行為。

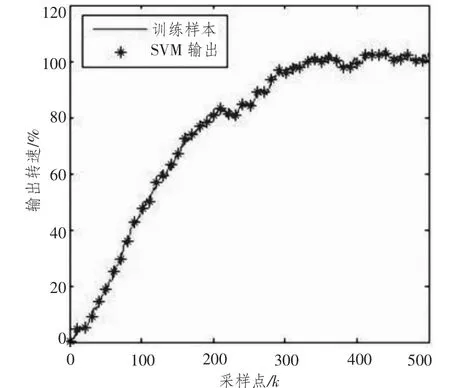
圖3　訓練樣本和支持向量機輸出對比Fig.3 Comparison between training data and SVM outputs

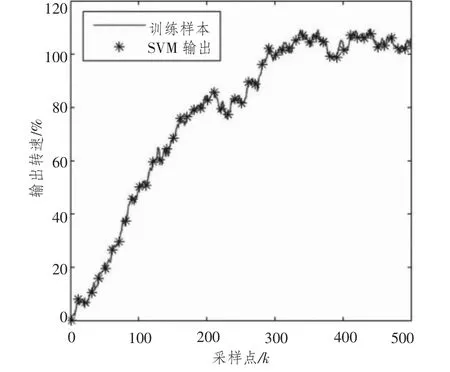
圖4　測試樣本和支持向量機輸出對比Fig.4 Comparison between testing data and SVM outputs

2.2控制系統的仿真

控制系統仿真結果如圖5和圖6所示，其中圖5為燃料供應量變化曲線，圖6為發動機轉速變化曲線，圖中的數據作了無量綱化處理。從仿真結果可看出，基于SVM的參數自整定PID控制系統響應快速，系統調節時間約為2 s，且無超調，表明該控制策略可以很好地完成魚雷發動機控制。

圖7展示了采用粒子群算法的收斂曲線。由圖可知，采用粒子群算法收斂至最小值只需要不超過

30步的迭代計算，表明該算法是一種高效快速的優化算法，可以滿足實時控制系統的要求。

圖5　燃油供應量的變化曲線Fig.5　Response of fuel flow rate

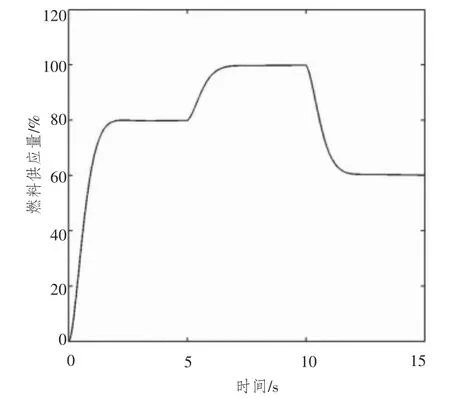
圖6　發動機轉速的變化曲線Fig.6　Response of engine rotation speed

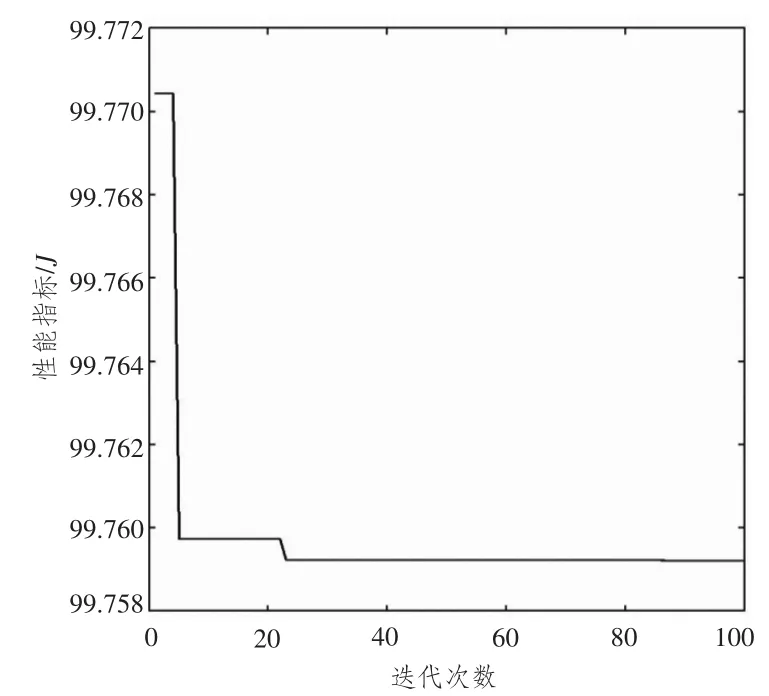
圖7　粒子群算法的收斂曲線Fig.7 Convergence curve of PSO algorithm

3　結語

本文針對魚雷發動機提出了基于支持向量機的參數自整定PID控制方法。與傳統PID控制相比，參數自整定PID的控制效果對于初始的kp，ki，kd參數不敏感，只需使初始的kp，ki，kd參數在一定的合理范圍即可，從而避免了精確整定PID參數的繁瑣工作。仿真實驗表明，支持向量機能很好地擬合發動機的動態特性，基于支持向量機的參數自整定PID控制器響應快速，無超調，控制效果良好。

參考文獻:

［1］王偉，張晶濤，柴天佑．PID參數先進整定方法綜述［J］．自動化學報，2000，26(3) :347－355．WANG Wei，ZHANG Jing-tao，CAI Tian-you．A survey of advanced PID parameter tuning method［J］．Acta Automatica Sinica，2000，26(3) :347－355．

［2］劉金琨．先進PID控制及其MATLAB仿真［M］．北京:電子工業出版社，2004．LIU Jin-kun．Advanced PID control and Matlab simulation ［M］．Beijing: PublishingHouseof Electronic Industry，2004．

［3］姚華，袁鴦，鮑亮亮，等．航空發動機神經網絡自學習PID控制［J］．推進技術，2007，28(3) :313－316．YAO Hua，YUAN Yang，BAO Liang-liang，et al．Selflearning PIDcontrol based on neural networks for aeroengines［J］．Journal of Propulsion Technology，2007，28 (3) :313－316．

［4］李秋紅，孫健國，周繼超．航空發動機PID控制參數優化的改進遺傳算法［J］．南京航空航天大學學報，2006，38 (2) :162－165．LI Qiu-hong，SUN Jian-guo，ZHOU Ji-chao．Improved algorithm for calculating GA Fitness function of aeroengine PID controller parameter optimization［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2006，38 (2) :162－165．

［5］VAPNIK V．The nature of statistical learning theory［M］．New York: Springer-Verlag，1999．

［6］SMOLA A J，SCHOLKOPF B．A tutorial on support vector regression［J］．Statistical Computation，2004 (14) : 199 －222．

［7］KENNEDY J，EBERHART R．Particle swarm optimization ［C］．Proceedings of IEEE International Conference on Neural Networks，1995:1942－1948．

［8］謝曉鋒，張文俊，楊之廉．微粒群算法綜述［J］．控制與決策，2003，18(2) :129－134．XIE Xiao-feng，ZHANG Wen-jun，YANG Zhi-lian．Overview of particle swarm optimization［J］．Control and Decision，2003，18(2) :129－134．

作者簡介:路駿(1986－)，男，博士后，研究方向為水下能源動力技術。

基金項目:中國博士后科學基金資助項目(2014M552503)

收稿日期:2014－06－30;修回日期: 2014－08－20

文章編號:1672－7649(2015) 07－0108－04doi:10.3404/j.issn.1672－7649.2015.07.024

中圖分類號:TJ630．1

文獻標識碼:A