基于頻率法和非線性靜力求解法對短吊索抗彎剛度的識別

王進軍　李萬霞　何有為

(1.中交二航局六公司　武漢　430014;　2.湖北興達路橋股份有限公司　咸寧　437100)

基于頻率法和非線性靜力求解法對短吊索抗彎剛度的識別

王進軍1李萬霞1何有為2

(1.中交二航局六公司武漢430014;2.湖北興達路橋股份有限公司咸寧437100)

摘要吊索彎曲剛度與多種因素有關，是一個未知的參數，在工程實踐中往往難以準確識別。文中選取了某懸索橋3 m長由直徑為5 mm高強鍍鋅鋼絲組成的吊索作為研究對象，采用頻率法和非線性靜力求解法分別推求短吊索的抗彎剛度，按修正后的抗彎剛度對吊索進行受力分析。結果表明，該懸索橋短吊索的球形轉動裝置可以取消，不僅可以降低工程成本，還便于日常養護。

關鍵詞頻率非線性短吊索剛度試件傳感器測點

吊索彎曲剛度與其內部結構形式、鋼絲間的粘結程度、結構的使用狀態、振動形式等因素有關，是一個未知的參數。在工程實踐中拉索的彎曲剛度往往難以準確識別[1]。目前，國內外常用的索力測定方法主要有壓力傳感器法、液壓千斤頂法、振動頻率法、磁通量法等幾種[2]。振動頻率法測試索力可考慮剛度影響，在索力已知的情況下，就可反推吊索剛度。

某懸索橋吊索采用73根直徑5.0 mm高強鍍鋅鋼絲組成，最短的吊索為2.813 m，由于橋面較窄，橫風作用下橫向變形較大，短吊索的剛度影響敏感。設計時為滿足短吊索橫向變形需要，橋跨中部17對較短的吊索上端設有球向轉動裝置。但該裝置構造復雜，增加養護難度和影響耐久性。施工時增加了專題研究，通過短吊索的彎曲剛度的研究，精確計算短吊索的應力，對短吊索的安全性進行評價，研究是否可取消吊索球向轉動裝置。

研究取3 m長的吊索作為試件，重點研究短吊索的彎曲剛度的識別方法，采用頻率法和非線性靜力求解法分別推求抗彎剛度，并對2種方法進行對比分析。

1試驗方案

1.1　試驗試件及儀器

取3 m長吊索作為試件，試驗裝置示意見圖1、圖2，試驗設備主要由吊桿及配套錨具試件、張拉臺座、張拉千斤頂、壓力傳感器、應變傳感器及數據采集系統，計算機、機電百分表、鋼絲繩等組成。

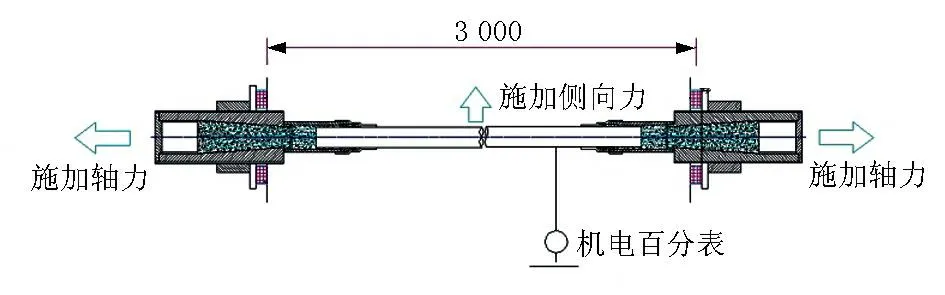
圖1　試驗裝置示意

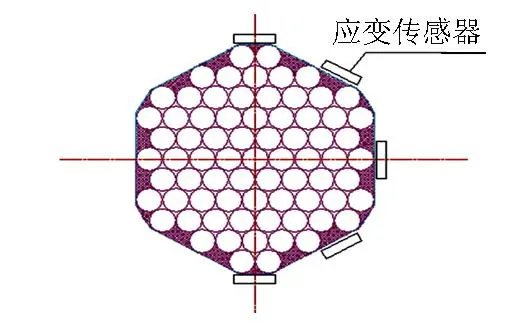
圖2　吊桿截面

1.2　測點布置

(1) 應力測點。在吊桿張拉端壓力傳感器沿圓周方向布置4個壓力盒，布置位置見圖3，從4個壓力盒和分別讀取壓力值，根據壓力值計算端部彎矩和軸力。

圖3　壓力盒布置位置示意

(2) 應變測點。在吊桿兩端和L/2截面附近(測試時需準確量測測點布置位置)處布置測量斷面，測量斷面沿圓周方向布置5個測點，分別讀取5個測點的應變值，通過應變推導截面的應力分布，驗證截面是否滿足平截面假定。

(3) 位移測點。在吊桿L/2、L/4和3L/4截面處布置撓度測點，測量以上斷面處的吊桿體的位移，位移由機電百分表直接測量。

1.3　試驗方案

試驗通過2種途徑分別測量吊桿的抗彎剛度：①頻率法，給吊桿施加軸力，通過頻率法識別抗彎剛度；②橫向加載靜力求解法，在吊桿跨中施加側向力，通過吊桿力和變形測試結果推算抗彎剛度。

1.3.1頻率法測抗彎剛度

(1) 在臺座上安裝吊桿，吊桿兩端擰緊螺母，墊圈下安放壓力傳感器。

(2) 按4組工況進行加載，加載值分別取破斷荷載的20%，30%，40%和60%，即160，320，480，640 kN。

(3) 對于每級荷載，在環境激勵下利用加速度傳感器拾取吊桿的隨機振動信號，然后通過頻域分析獲取吊索的頻譜圖，據此識別出斜拉索的各階振動固有頻率。

(4) 通過理論分析(解析法與有限元法)與現場標定，獲取吊桿索力與振動固有頻率之間的對應關系。

(5) 根據實測的各階頻率及上述關系，識別吊索抗彎剛度。

1.3.2橫向加載法測抗彎剛度

(1) 在臺座上安裝吊桿，吊桿兩端擰緊螺母，墊圈下安放壓力傳感器。

(2) 按4組工況進行吊桿張拉加載，加載值分別取破斷荷載的10%，20%，30%和40%，通過橫向加載，使吊桿力控制到設計荷載的20%，30%，50%和80%，即160，320，480，640 kN。

(3) 首先精確測試初始垂度，對于每級荷載，分別根據百分表讀取吊桿的撓度、吊桿測量截面的應變、壓力盒讀數，以及千斤頂油壓表讀數。

(4) 結合應變、撓度以及壓力分布值推算吊桿的抗彎剛度。

2試驗結果分析

2.1　分析理論

2.1.1頻率法

(1) 基本原理。利用頻率法測試索力是測試結構自振頻率、分析其自振特性從而求出索力的方法。將索力動測儀的拾振器附著于吊桿, 拾取吊桿的振動信號, 經過濾波、放大、譜分析, 得到吊桿的自振頻率, 然后根據索力與吊桿頻率間的固有關系來確定索力。

應用結構動力學原理，建立吊桿的微分振動方程。

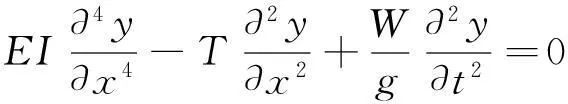
式中:EI為吊桿的彎曲剛度；x為沿吊桿軸向的坐標,m；y為吊桿的振幅,m;T為吊桿的索力,N;W為吊桿單位長重量,N/ m。其中第一項體現了抗彎剛度對吊桿振動的影響。

(2) 給對索力求頻率。采用有限元法對吊桿進行自由振動分析, 可得如下特征方程。

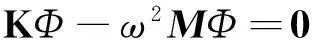
式中：M為質量矩陣；K為剛度矩陣；ω為固有圓頻率，Φ為振型。

對于某一給定的吊桿力T, 根據初應力剛度矩陣可進行靜力求解獲取索應力后得到。求解上述特征方程即可得到在T作用下斜拉索的各階固有頻率fi(i=1,2,…,n)，i為頻率階數；n為所考慮的最高階頻率的階數。

(3) 索力、頻率關系的數值擬合。利用解析法的實用公式初步估算吊桿力范圍，在此范圍內取多個吊桿力，求解出各個吊桿力作用下的頻率，通過數值擬合確定吊桿力與頻率的關系。

Ti=Ti(fi)

(4) 抗彎剛度識別。在合理范圍內將抗彎剛度按0.05(EI)max的步長進行遞增，對應每個抗彎剛度，可得出一族吊桿力與頻率的關系曲線。根據實測各階頻率和假定的抗彎剛度推求吊桿力，將所得吊桿力與實測吊桿力進行對比來識別抗彎剛度。另外，由于索力是惟一的，因此不同頻率數的實測索力應該一致，據此也可識別抗彎剛度。

2.1.2非線性靜力求解法

(1) 基本原理。首先對吊桿進行側向加載，使吊桿產生彎曲變形，吊桿兩端邊界條件通過端部測點應力測試識別，計入幾何非線性，根據靜力求解方法識別抗彎剛度。

(2) 彎矩剛度的有限元識別。在每級加載工況下，抗彎剛度按0.05(EI)max的步長進行遞增，對應每個抗彎剛度，采用非線性有限元方法求解所需的內力及位移(端部彎矩、吊桿體的撓度和測量截面的應變)，根據實測的內力及位移參數識別抗彎剛度。

(3) 彎矩的理論識別方法。根據實測的端部壓力分布，考慮非線性效應，根據撓度和應變推求抗彎剛度。

2.2　試驗結果

非線性靜力求解法由于橫向位移較小，橫向力較小時受測試精度影響，分析結果很不理想，但在最后兩級試驗荷載時，將實測數據利用有限元進行試算模擬，相關參數可保持一致，識別的抗彎剛度與頻率法測試識別的也基本一致，起到了驗證效果，頻率法試驗結果見表1，利用下式計算出吊索剛度。

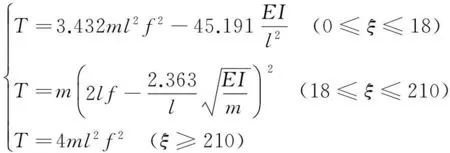
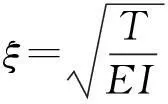
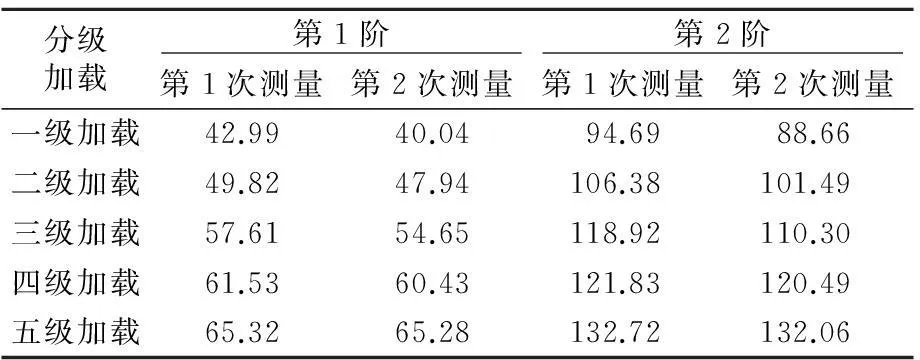
表1　短吊索試驗結果　Hz

通過對比分析，確定出吊索在其使用荷載下的抗彎剛度EI=1.24e9mm2, 是鋼絲疊加抗彎剛度的2.84倍，但僅為換算整體截面抗彎剛度的3.9%。利用實測抗彎剛度對吊索橫向受力進行計算分析，考慮剛度折減后短吊索受力可滿足要求，可取消球形轉動鉸。

3結語

通過采用頻率法和非線性靜力求解法對吊索抗彎剛度的識別，按修正后的抗彎剛度對對吊索受力進行分析后取消了短吊索的球形轉動裝置，有利于日常養護，研究結論可供存在短吊索的工程參考。但必須認識到在不同荷載作用下，吊索抗彎剛度變化很大，其值與吊索內部結構形式、鋼絲間粘結強度、結構試驗狀態等有關，是一個不易識別的參數，工程應用時應以實際測試為準。采用非線性靜力求解法時，應事先對試驗方案進行詳細規劃，避免因測試精度不足造成結果分析困難。

參考文獻

[1]陳舒婷,吳惠君,范中林,等.考慮彎曲剛度及邊界約束的短索內力識別[J].交通科技,2013(1):26-28.

[2]凌知民,沈紅,沈炯偉.吊桿索力的計算方法與應用研究[J].石家莊鐵道大學學報,2011(3):35-36.

Identification for Flexural Rigidity of Short Suspension Cable

Based on Frequency Method and Nonlinear Static Method

WangJinjun1,LiWanxia1,HeYouwei

(1.No.6 Eng. Co. Ltd. of CCCC Second Harbor Engineering Co., Ltd., Wuhan 430014, China;

2.Hubei Xingda Road & Bridge Co., Ltd., Xianning 437100, China)

Abstract：Suspension cable bending stiffness is related to a variety of factors. As an unknown parameter, the suspension cable bending stiffness is difficult to be identified accurately in actual engineering. In this paper a 3m long sling being made up of 5mm diameter high-strength galvanized steel wires is selected as the research subject. The frequency method and nonlinear static solution are used to estimate short sling bending stiffness. Amended bending stiffness is taken to stress analysis of the sling. The results show that the spherical rotation means of the short sling can be canceled, which will reduce the project cost, and is beneficial to routine maintenance.

Key words:frequency; nonlinear; short suspension cable; stiffness; specimen; sensor; measure point

收稿日期：2015-08-15

DOI 10.3963/j.issn.1671-7570.2015.06.003