沖擊功與斷裂韌度經驗關系式對Q345R鋼的適用性

崔慶豐，惠 虎，王昊旸， 李培寧

(1.華東理工大學機械與動力工程學院，承壓系統及安全教育部重點實驗室， 上海 200237；

2.中國特種設備檢測研究院， 北京 100013；3.北京航空航天大學材料科學與工程學院， 北京 100191)

?

沖擊功與斷裂韌度經驗關系式對Q345R鋼的適用性

崔慶豐1，惠 虎1，王昊旸2,3， 李培寧1

(1.華東理工大學機械與動力工程學院，承壓系統及安全教育部重點實驗室， 上海 200237；

2.中國特種設備檢測研究院， 北京 100013；3.北京航空航天大學材料科學與工程學院， 北京 100191)

摘要：以我國最常用的壓力容器用Q345R鋼為研究對象，進行了沖擊和斷裂韌性試驗；收集整理了國際標準中應用廣泛的斷裂韌度經驗關系式，結合實測的材料性能數據，對這些關系式用于估算Q345R鋼在轉變溫度區內斷裂韌度的準確性進行了對比分析。結果表明：Sailors-Corten及Wallin關系式對斷裂韌度的預測結果與實測的結果符合性最好，在轉變溫度區內，可用于估計Q345R鋼的斷裂韌度；在實測材料性能數據的基礎上,修訂建立了適用于Q345R鋼的沖擊功與斷裂韌度的經驗關系式。

關鍵詞：經驗關系式；沖擊功；斷裂韌度

0引言

二次世界大戰期間，數以百計的焊接輪船在大洋中發生脆性斷裂事故，美國海軍實驗室在對輪船脆斷事故分析的基礎上提出了著名的15ft-lb(20 J)準則，同時將沖擊試驗作為材料韌性的衡量方法，在世界范圍內被廣泛采用[1]。19世紀50年代末到60年代初，世界范圍內發生了多起厚截面壓力容器在水壓試驗時的脆斷事故，有些容器發生脆斷時的應力甚至遠低于設計應力。當時的容器設計僅考慮強度要求，而對材料韌性沒有具體規定，正是在這樣的背景下20 J能量準則也被用于壓力容器制造行業。盡管輪船與壓力容器在服役環境、結構特點以及應力分布等方面存在諸多差異，但是20 J能量準則是與當時的鋼鐵冶金、壓力容器制造加工水平相適應的，因此20 J能量準則的采用使得壓力容器脆斷事故的發生率大為降低[2]。雖然沖擊試驗沒有嚴密的理論基礎，沖擊功也不能直接用于計算，但是其經濟、方便的優點使其成為控制鋼鐵材料質量、衡量鋼鐵韌性的必要手段[3]。20世紀60年代發展起來的斷裂力學，針對含缺陷構件(裂紋體)的斷裂韌性參數(K、CTOD、J)值給出了更為精確的描述，這些韌性參數能夠直接用于結構完整性評定計算，使得重要的高參數構件(如導彈、核容器)的設計更加安全合理。長期以來人們都試圖尋找沖擊功與斷裂韌度之間的聯系，期望以沖擊功替代斷裂韌度用于計算。但是沖擊試驗與斷裂韌性試驗在加載速率、試樣尺寸以及缺口類型上的差別，使得二者在理論上的關聯變得十分困難。20世紀70年代Barsom以及Sailors等進行了大量的沖擊試驗與斷裂韌性試驗[4-5]，在此基礎上提出了一系列沖擊功(AKV)與靜態斷裂韌度(KIC)及動態斷裂韌度(KId)的經驗關系式，這些關系式甚至成為某些壓力容器規范防脆斷規定的內在要求。隨著現代斷裂力學的發展，J積分的出現使得人們嘗試從能量的角度建立J與AKV的關系[6]，同時也有研究人員用局部法理論試圖消除缺口與裂紋之間的差別，建立二者之間的聯系[7]。由于目前斷裂韌度隨溫度變化關系曲線(如ASME參考韌性曲線、主曲線Master Curve等)大多用指數方程表示，因此文獻[8]嘗試用指數方程代替雙曲正切方程擬合沖擊功數據。示波沖擊機的出現，使得沖擊功中起裂能、擴展能以及撕裂能能夠被區分開來，從而可選取其中一部分與斷裂韌度進行關聯[9]。盡管相關的研究報道很多，但是目前仍未能從理論上建立沖擊功與斷裂韌度之間的聯系。

鐵素體鋼轉變溫度區內斷裂韌度往往呈高度分散，因此如何科學合理地處理轉變溫度區內斷裂韌度數據成為長期以來困擾工程界的一大難題，直到主曲線法(Master Curve)的出現這一問題才得到很好的解決[10]。主曲線為對應于失效概率50%的斷裂韌度曲線，其斷裂韌度KJC為100 MPa·m1/2，對應的溫度即為參考溫度T0MC。根據T0MC即可獲得任意失效概率下材料在韌脆轉變區的斷裂韌度。主曲線法可以描述鐵素體鋼在韌脆轉變區斷裂韌度的分布情況，該方法的最大優勢在于用少量的小尺寸試樣即可測試得到材料的參考溫度，目前該方法已經被美國材料試驗協會標準化采用并推出標準ASTM E1921。

沖擊功與斷裂韌度轉變溫度曲線之間也并非簡單的平移就能相互轉換[11]，鋼鐵材料的斷裂韌度與沖擊功的轉變溫度相差較大且曲線形狀存在差異，因此目前能夠應用于工程并被寫入規范的關系式仍是建立在二者試驗數值關聯的基礎上，一為KIC與AKV數值關系式，二為二者特征溫度的關系式。Q345R鋼是我國使用最廣泛的壓力容器用鋼，在工程實踐中要測得其KIC往往是不現實的，而參數JIC的測試也需要一定尺寸的材料，費時費力，尤其是在對在役設備進行評定時，實際測試材料的斷裂韌度幾乎是不可能的，因此就需要用簡單的沖擊試驗結果去估計材料的斷裂韌度。然而現行規范中的經驗關系式不僅數量繁雜，而且往往是20世紀70年代推導出來的。而今無論是鋼鐵冶煉水平，還是機械加工制造水平都較過去有了突飛猛進的進步，用過去的經驗關系式去評價當代材料勢必會產生較大的保守性。為此，作者以我國常用的壓力容器用Q345R鋼為研究對象，基于實測的斷裂韌度與沖擊功數據，考察了這些經驗關系式對Q345R鋼的適用性，進一步給出了偏于安全又不過分保守的可用于估計Q345R鋼斷裂韌度的經驗關系式。

1試樣制備與試驗方法

試驗材料為Q345R鋼板，正火態，厚度分別為30，50，60，80 mm。

在Q345R鋼板上沿橫向切取尺寸為10 mm×10 mm×55 mm的沖擊試樣，開V型缺口，按照GB/T 229-2007進行沖擊試驗，最大沖擊能量為300 J，沖擊速度為5 m·s-1，測試溫度為-90～50 ℃，測試結果見圖1。

圖1　不同溫度下Q345R鋼的沖擊功Fig.1　Impact energy of Q345R steel at different temperatures

分別在厚度為36，80 mm的Q345R鋼板上切取25 mm厚的標準三點彎曲(SEB)試樣，試樣縱向垂直于軋制方向，裂紋擴展方向沿軋制方向，按照ASTM E1921-15，在Instron8032型多功能試驗機上進行斷裂韌性試驗。SEB試樣在酒精加液氮的混合溶液中低溫冷卻，試驗溫度為-70 ℃，保溫1 h后開始試驗，其間通過不斷補充液氮并持續攪拌來保證溫度的均勻性，試驗結果見圖2。計算得到36 mm厚鋼板上切取的試樣其參考溫度T0MC為-96.6 ℃，80 mm厚鋼板的T0MC為-89.3 ℃，為了得到一個保守的結果，在以后的計算中統一采用80 mm厚鋼板的參考溫度，即-89.3 ℃。

圖2　Q345R鋼主曲線以及5%、95%邊界線Fig.2　Master Curve of Q345R steel with upper andlower tolerance bounds of 5% and 95%

2沖擊功與斷裂韌度經驗關系式及其預測結果

2.1　沖擊功與斷裂韌度經驗關系式

表1中給出了國際上應用較多或被寫入規范的若干經驗關系式，表中σy為材料的屈服強度。關系式(B)和(E)被稱為WRC265關系式，是Sailors[12]分析了大量的沖擊功以及斷裂韌度數據后給出的，其材料種類多、數據范圍較廣，但文獻中并沒有給出具體的AKV范圍和材料種類。關系式(A)～(C)為KIC關系式，而關系式(D)～(G)為KId關系式，KId需要由式(1)和(2)(移位公式)換算到KIC。

(1)

(2)移位公式是Barsom等[13]分析了屈服強度在250～965 MPa的多種材料的KId與KIC數據得到的，該移位公式最初是配套關系式(F)使用的。為了方便對比，關系式(C)和(F)中的彈性模量統一規定為200 GPa。由于表1中經驗關系式數量多且種類不一，因此這里分別將關系式(A)～(C)、關系式(D)～(G)進行對比分析。

表1　常用的轉變溫度區AKV與KIC經驗關系式Tab.1　Frequently-used empirical correlations between AKV and KIC in transition temperature range

圖3(a)為關系式(A)～(C)計算曲線，可見，在相同的AKV下，采用關系式(B)計算得到的KIC值最小，關系式(A)的結果次之，關系式(C)的最大；圖3(b)為關系式(D)～(G)計算曲線，其中采用關系式(E)得到的KId值最小，關系式(D)的次之，關系式(G)的最大，關系式(F)的介于關系式(D)與(G)的之間。

圖3　不同關系式的沖擊功和斷裂韌度關系曲線Fig.3　Impact energy vs fracture toughness curves calculated by different correlations

為了便于對比，采用圖1中沖擊數據的下邊界值參與分析，見式(3)，而斷裂韌度值則采用歐美主要的結構完整性規范如API579、BS7910、R6以及SINTAP所推薦的5%失效概率斷裂韌度曲線作為材料斷裂韌度的保守估計值[14]，見式(4)。

(3)

KJC(0.05)=25.2+36.6exp[0.019(T-89.3)]

(4)

2.2　經驗關系式預測的準確性

選取式(3)計算結果作為Q345R鋼沖擊功的輸入值，而式(4)的結果作為斷裂韌度的實測值，與經驗關系式的預測值比較。由于經驗關系式適用區間為轉變溫度區，因此式(3)的使用范圍為溫度不高于-28 ℃。基于圖3的分析選擇關系式(B)，(E)(最保守)和關系式(A)，(D)(次要保守)參與對比分析，結果見圖4。

同步電動機因無磁極檢測單元，無論接至電網或由他控變頻電源饋電，完成起動后進入穩定運行時必須具備電源頻率恒定、電壓和勵磁保持不變的條件。因此，式(1)中的轉子轉速Ω、電壓U、空載電動勢E0及同步電抗Xs等物理量及參數皆為定值，所以，同步電動機的電磁轉矩T是唯一的變量即功角δ之正弦函數。

圖4　由沖擊功估計Q345R鋼斷裂韌度的經驗關系式預測結果Fig.4　Predicted results of fracture toughness of Q345R steelestimated by empirical correlations with impact energy

由圖4可知，由于受到轉變溫度區間的限制，動態斷裂韌度關系式的適用范圍局限于轉變溫度區內很小的區域，在這個區域內關系式(D)高估了材料的斷裂韌度，關系式(E)(Sailors-Corten)的預測結果較好；靜態斷裂韌度關系式在轉變溫度區內先是低估后又高估了材料的斷裂韌度，對比來看關系式(A)(Sailors-Corten)給出的估計值較為接近實測值。由于KId的測試一直缺乏一個標準規范[15]，早期的KId測試方法以及合格標準往往會因測試者不同而存在很大差別，因此文獻中KId數據的有效性是值得懷疑的，表1中動態斷裂韌度關系式對于Q345R鋼是不適用的。

此外，靜態斷裂韌度關系式的預測結果也不是太理想，主要是因為：首先這些經驗關系式是基于當時鋼材試驗數據得到的，而Q345R鋼是當代鋼鐵冶金產品，其韌性和質量都有了大幅提升；其次這些經驗關系式是建立在斷裂韌度與沖擊功之間的數值關系上的，因此數據樣本的大小直接關系到關系式預測的準確性；最后,這些經驗關系式是基于多種不同材料的試驗數據得到，其預測對象也是不區分材料種類的，但是事實是不同種類材料即使沖擊功相同，其斷裂韌度也可能相差很大，劉長軍[16]收集了53組針對多種材料的JIC/AKV數據，發現該數值介于0.86～12.31之間。因此有必要建立一個專門針對Q345R鋼的斷裂韌度-沖擊功經驗關系式。

作者采用式(3)和式(4)來進行公式推導，數值采用試驗數據的下包絡線值(見圖1)以保證所建立經驗關系式的保守性；式(4)可以描述材料在韌脆轉變區斷裂韌度的分布情況，因此能擺脫經驗關系式對數據樣本量的依賴性。通過式(3)與(4)在韌脆轉變區的分析與求解，作者得到了適用于Q345R鋼的沖擊功與斷裂韌度的經驗關系式：

(5)

3特征溫度T28J與TK100的經驗關系式

早期人們常常選擇沖擊功28 J、斷裂韌度100 MPa·m1/2作為材料韌性標準指標。隨著鋼鐵冶金技術的進步，28 J幾乎成為了壓力容器用鋼的最低要求。從已有的沖擊功數據來看，對于壓力容器用鋼而言，28 J的水平基本處于轉變溫度曲線的下轉變區，這意味著28 J處于沖擊能量由下平臺向轉變區過渡的階段，該參數的意義與Barsom[17]關于轉變溫度的定義是一致的；選擇100 MPa·m1/2作為材料的斷裂韌性指標，首先受到當時彈塑性斷裂力學發展的限制，斷裂模式必須以脆性斷裂為主導，其次是因為大量的實踐案例證明當材料斷裂韌度達到100 MPa·m1/2時，脆斷發生的幾率大為降低。20世紀80年代人們針對沖擊功28 J對應的特征溫度T28J與斷裂韌度100 MPa·m1/2對應的特征溫度TK100之間的關系開展了廣泛的研究，其中最為成熟且應用廣泛的主要有Sanz[18]與Wallin[14]提出的經驗關系式。

3.1　Sanz經驗關系式

在大量試驗數據的基礎上，Sanz提出了T28J與TK100的經驗關系式和斷裂韌度隨溫度變化的關系式：

(6)

(7)

式中：K0為25 MPa·m1/2；KIC0為沖擊試驗溫度下的斷裂韌度，100 MPa·m1/2；β=1/60 ℃;ΔTe為考慮厚度尺寸效應的溫度修正值。

聯立式(6)和(7)，便可由沖擊試驗結果換算得到斷裂韌度，同時式(6)與(7)也是構成法國壓力容器標準CODAP中材料部分低溫設計圖線的內在韌性要求[19]，式(7)還被瑞典壓力容器規范中低溫防脆斷條款所采用[20]。

3.2　Wallin經驗關系式

通過對多種材料在轉變溫度區大量數據的分布規律研究，Wallin提出用三參數Weibull分布來描述鐵素體鋼在韌脆轉變區內任意溫度下斷裂韌度的概率分布，假定所有鐵素體鋼隨溫度變化的曲線形狀相同，材料韌性的好壞僅體現在斷裂韌度隨溫度變化曲線沿溫度軸左右的平移，即材料韌性越好其參考溫度T0MC越低，只要求得T0MC即可得到任意失效概率下的斷裂韌度，計算公式如下：

KJC=20+{11+77exp[0.019(T-T0MC)]}×

(8)

在分析了大量韌轉變溫度區斷裂韌度與沖擊功數據的基礎上，Wallin得到了特征溫度T28J與TK100的經驗關系式：

(9)

式中：σ為標準差，用以表示斷裂韌度、沖擊功以及經驗關聯式三方面的不確定性[21]。

作者收集整理了屈服強度在300～1 500 MPa之間、厚度在10～250 mm之間的母材與焊縫試樣，其包含線彈性斷裂韌度KIC與彈塑性斷裂韌度KJC在內的363個T28J與TK100的數據，與式(6)，(9)擬合曲線進行了對比，見圖5。由圖5可知，式(9)擬合曲線與試驗數據的相關性較好，大部分數據點落入±2σ范圍內；而式(6)的曲線與數據的相關性較差，其對TK100先是給出了偏低的估計值，隨著T28J的升高，又給出偏高的估計值。作者試驗所得到的數據也隨機地分布于式(9)的±2σ分散帶內，驗證了式(9)對Q345R鋼特征溫度良好的預測效果。

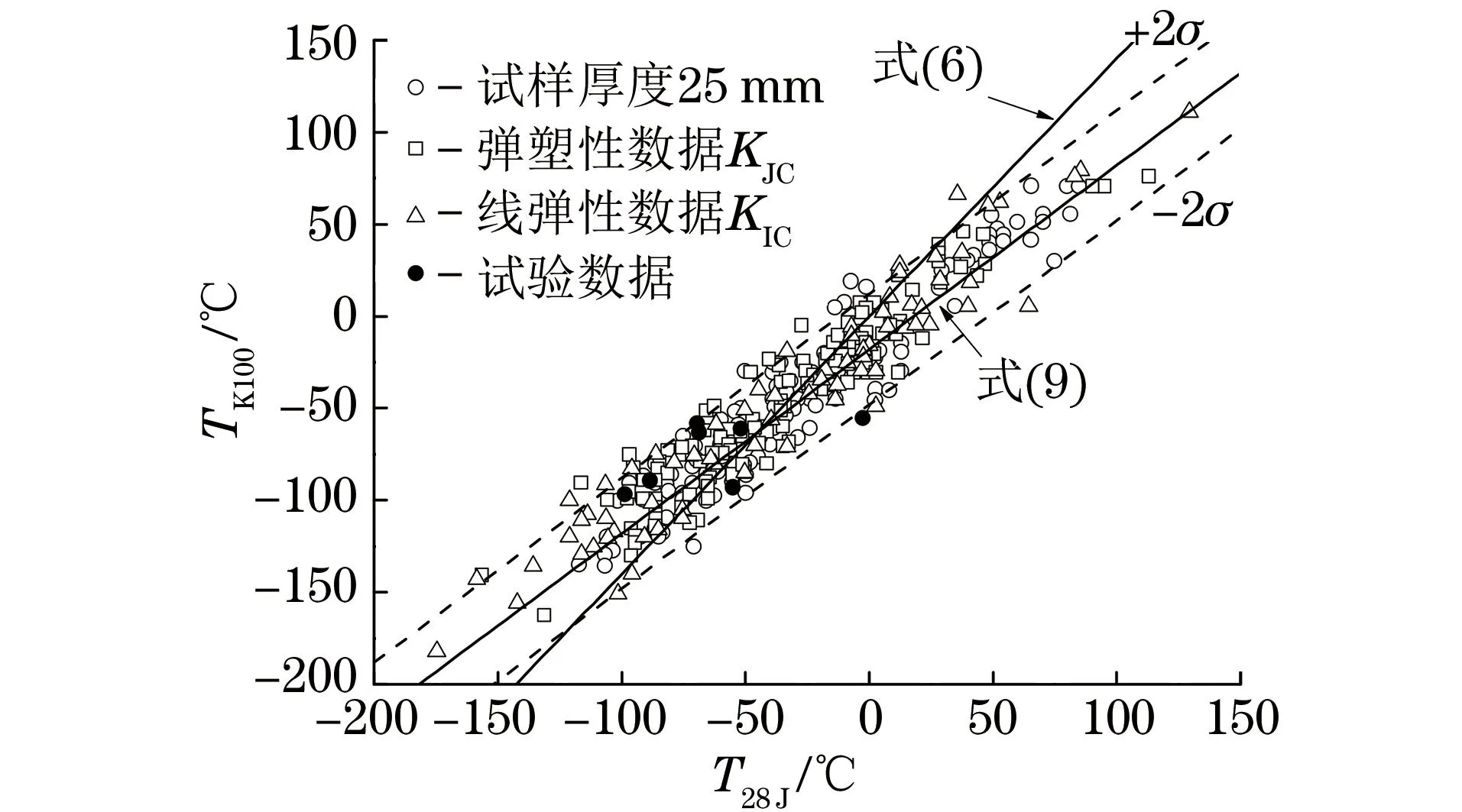
圖5　不同經驗關系式計算得到T28J與TK100關系曲線及試驗數據Fig.5　T28J vs TK100 curves calculated by different empiricalcorrelations and experimental data

這里以80 mm厚Q345R鋼板實測的材料性能數據，考察式(6)，(9)，(10)對TK100的預測效果。由表2可知，式(6)與(9)的計算值均低于試驗值，這就意味著在同一溫度下預測得到的斷裂韌度要高于實測值。

相比之下，Wallin模型的預測結果較Sanz模型預測結果偏于安全,結果見圖6，圖6是在試樣厚度為25 mm基礎上得到的。在實際應用中式(9)常常被用作估計主曲線法測試的試驗溫度，而特征溫度TK100則是采用式(10)來估算：

(10)

式(10)中的25 ℃為額外增加的安全裕度，對應置信度90%標準差15 ℃的情況，安全裕度25 ℃被廣泛地應用于英國、法國、瑞典等國壓力容器規范防脆斷設計中[19-20]，也被應用于歐盟EN13445規范低溫設計圖線的制定[22-23]。

表2　TK100試驗值與不同關系式的預測值Tab.2　Experimental and predicted values bydefferent correlations of TK100　℃

從圖6可以看出，利用式(10)得到的斷裂韌度隨溫度變化的曲線最為保守且靠近實測主曲線，因此式(10)用于斷裂韌度特征溫度TK100的估計是合適的。

圖6　不同經驗關系式預測斷裂韌度隨溫度的變化曲線Fig.6　Fracture toughness vs temperature curves predictedby different empirical correlations

綜上所述，Sanz模型中特征溫度經驗關系式與試驗數據的相關性較差，同時式(7)預測的斷裂韌度曲線過高地估計了材料實際的斷裂韌度[20]。相比之下，Wallin的主曲線模型經驗關系式的預測結果與試驗數據的相關性很好，式(10)給出的特征溫度TK100稍高于實測值，繼而得到偏于保守又接近實測的斷裂韌度，目前該方法已經標準化，因此作者也推薦使用式(10)和(8)用于斷裂韌度的估計。

3.3　由轉變溫度區內其他特征溫度估計T28J

在多數情況下T28J是不能直接得到的，如鋼材的質量規范或標準往往僅規定材料在特定溫度下的沖擊能量滿足一定的要求，并沒要求這個沖擊功必須恰好等于28 J，因此在這種情況下必須能夠由已知沖擊功的試驗溫度TAKV推導得到T28J。歐盟EN1993以及EN13445標準中分別規定了T28J=T30J和T28J=T40J-10 ℃，作者利用實測的Q345R鋼沖擊試驗數據對這兩個公式進行了檢驗。

目前由特征溫度估計T28J的轉換公式主要有兩個，見式(11)和(12)。

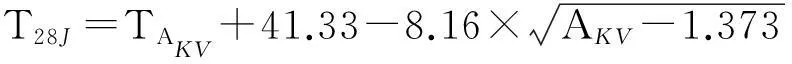
(11)

T28J=TAKV-

(12)

式中:AKVus為沖擊能量上平臺值。

其中使用式(11)需要滿足16 J≤AKV≤67 J,17 ℃≤TAKV-T28J≤25 ℃[24]，而式(12)僅要求用于推導T28J的沖擊能量AKV接近28 J[21]，但是使用式(12)時必須已知材料屈服強度值與沖擊能量上平臺值AKVus。

表3中列出了不同厚度的Q345R鋼板沖擊試驗數據以及由式(11)和(12)計算所得的T28J數據。由表3可以看出，實測的特征溫度T30J與T28J相差2～3 ℃，而T40J與T28J相差8～15 ℃，由此可見EN1993和EN13445標準中T28J與T30J以及T40J之間的轉換關系是保守的偏于安全的。式(11)與(12)的預測結果顯示，兩個公式基于T30J參數得到的T28J值與實測值相差在1.2 ℃以內，結果較為理想；而基于T40J參數的預測結果與實測值之間偏差較大，但均在6 ℃以內且預測值高于實測值，這主要是由于式(11)與(12)都是基于大量的試驗基礎，假定中低強度鋼在轉變溫度區內的沖擊功隨溫度變化曲線形狀相同[25]而推導得到的，因此能量水平離28 J越近其特征溫度估計值越準確。與Q345R鋼板實測的結果對比可以看出，利用式(11)與(12)估計T28J是可行的，但為保證預測精度,用于預測的沖擊能量值必須盡量接近28 J；同時兩式的預測效果相當，但在很多情況下尤其是上平臺沖擊能量值是無法得知的，因此在同等條件下應該優先選用式(11)。

表3　特征溫度轉換公式預測得到的Q345R鋼T28J和實測值Tab.3　Predicted results of T28J of Q345R by different characteristic temperature conversion formulas and measured values

4結論

(1) 在眾多沖擊功與斷裂韌度經驗關系式中，Sailors-Corten關系式對Q345R鋼斷裂韌度的預測結果與試驗值符合性最好；基于實測的沖擊功與斷裂韌度數據，得到了適用于Q345R鋼的沖擊功與斷裂韌度的經驗關系式，但公式本身的準確性仍需大量的數據驗證。

(2) Wallin提出沖擊功特征溫度T28J與斷裂韌度特征溫度TK100的經驗關系式對斷裂韌度的預測準確性優于Sanz關系式的，在已知T28J的情況下，可以利用Wallin關系式對材料的斷裂韌度進行估計，其與實測值相比較結果偏于保守；當參數T28J未知時，可以按照T28J=T30J與T28J=T40J-10 ℃進行換算，也可按照式(11)與(12)進行換算，但是換算時沖擊功應盡量接近28 J。

參考文獻：

[1]TOTH L, ROSSMANITH H P, SIEWERT T A. Historical background and development of the Charpy test[J]. European Structural Integrity Society, 2002,30:3-19.

[2]SMITH N, HAMILTON I G. Failure in heavy pressure vessels during manufacture and hydraulic testing [J]. West Scotland Iron Steel Inst, 1968/1969,76:117-87.

[3]王墉哲,劉俊亮,丁晨.熱軋高強鋼低溫沖擊功偏低的原因分析[J].機械工程材料, 2015,39(2):81-84.

[4]BARSOM J M, ROLFE S T. Correlations betweenKICand Charpy V-notch test results in the transition-temperature range[C]//Impact Testing of Metals. Atlantic: ASTM, 1970:281-302.

[5]SAILORS R H, CORTEN H T. Relationship between material fracture toughness using fracture mechanics and transition temperature tests[C]//Fracture toughness:Part Ⅱ.[S.l.]:ASTM,1972:150-163.

[6]HüBNER P, PUSCH G. Correlations between Charpy energy and crack initiation parameters of theJintegral concept[J]. European Structural Integrity Society, 2002:30:289-295.

[7]SMITH R J, SHERRY A H, HORN A J, et al. An engineering procedure for calculating cleavage fracture toughness from chapy specimen data using a mechanistic approach for ferritic steels[C]∥ASME 2014 Pressure Vessels and Piping Conference. Anaheim, California, USA:ASME,2014:1-12.

[8]ERICKSONKIRK M A, ERICKSONKIRK M T, ROSINSKI S, et al. A comparison of the tanh and exponential fitting methods for Charpy V-notch energy data[J]. Journal of Pressure Vessel Technology, 2009,131(3):031404.

[9]CVETKOVSKI S. Instrumented testing of simulated Charpy specimens made of microalloyed Mn-Ni-V steel[J]. European Structural Integrity Society, 2002,30:95-102.

[10]惠虎,王佳歡,王仙河,等.基于主曲線方法確定2.25Cr-1Mo鋼韌脆轉變區的斷裂韌度[J].機械工程材料, 2015,39(1):98-101.

[11]秦江陽，王印培，柳曾典.JIC和沖擊功AKV之間的關系研究[J].壓力容器, 2001,18(2):15-18.

[12]ROBERTS R, NEWTON C. Interpretive report on small scale test correlations withKICdata[J]. WRC Bulletin, 1981，265:1-18.

[13]BARSOM J M, ROLFE S T. Fracture and Fatigue Control in Structures: Application of the Fracture Mechanics[M]. Third Edition.[s.l.]: ASTM, 1999:119-120.

[14]WAILLIN K, NEVASMAA P, PLANMAN T, et al. Evolution of the Charpy-V test from a quality control test to a materials evaluation tool for structural integrity assessment[J]. European Structural Integrity Society, 2002,30:57-68.

[15]BARSOM J M, ROLFE S T. Fracture and Fatigue Control in Structures: Applications of the Fracture Mechanics[M]. First Edition. [s.l.]: ASTM, 1977:125-140.

[16]劉長軍，李培寧，孫亮,等. 管道評定用AKV值估算JIC下限值的工程方法[J].壓力容器, 1999,16(6):7-13.

[17]BARSOM J M. Development of the ASSHTO of fracture toughness requirements for bridge steels[J]. Engineer Fracture Mechanics, 1975,7:605-618.

[18]MARANDET B, SANZ G. Evaluation of the toughness of thick medium strength steels by using linear elastic fracture mechanics and correlations betweenKICand Charpy V-notch toughness[M]//Pro Conf Flaw Growth and Fracture, STP 631. Philadelphia: ASTM, 1977:72-95.

[19]SANZ G. Attempts to introduce a quantitative method of choosing steel quality with reference to the risk of brittle fracture[J]. Rev Metall CIT, 1980,77:621-642.

[20]SANDSTR?M R. Minimum usage temperature for ferritic steels[J]. Scand J Metall, 1987,16:242-52.

[21]WALLIN K. Guidelines for deriving fracture toughness estimates from normal and miniature size Charpy-V specimen data[J]. Rakenteiden Mekaniikka, 1992,25(3):24-40.

[22]WIESNER C S, SANDSTR?M R, GARWOOD S J, et al. Background to requirements for the prevention of brittle fracture in the European standards for pressure vessels (prEN 13445) and metallic industrial piping (prEN 13480)[J]. Int J Pres Ves Pip, 2001,78:391-399.

[23]DAWES M G, DENYS R. BS5500 appendix d: an assessment based on wide plate brittle fracture test data[J]. Int J Press Vessel Piping, 1984,15:161-92.

[24]KUHN B. Beitrag zur vereinheitlichung der europaisehen regelungen zur vermeidung yon sprodbrueh[D]．Aacheni: Rheinisehe-Westfael Technische Hochschule, 2005.

[25]PISARSKI H G, HAYES B, OLBRICHT J, et al. Validation of idealised Charpy impact energy transition curve shape[J]. European Structural Integrity Society, 2002,30:333-340.

Applicability of Empirical Correlations between Impact Energy

and Fracture Toughness for Q345R Steel

CUI Qing-feng1, HUI Hu1, WANG Hao-yang2,3, LI Pei-ning1

(1.Key Laboratory of Safety Science of Pressurized System, Ministry of Education,

School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China;

2.China Special Equipment Inspection and Research Institute, Beijing 100013, China;

3.School of Materials Science and Engineering, Beihang University, Beijing 100191, China)

Abstract:The most commonly used pressure vessel steel Q345R in China was investigated by means of the impact test and fracture toughness test. The widely used empirical correlations of fracture toughness in the international standards were collected. Combining with the experimental data of material properties, the accuracy of these correlations used to estimate the fracture toughness in the transition temperature range of Q345R steel was analyzed. The results show that the Sailors-Corten and Wallin empirical correlations have good agreement with the measured fracture toughness and can be used to estimate the fracture toughness of Q345R steel during the transition temperature range. Furthermore, the specific correlation between impact energy and fracture toughness for Q345R steel was established based on the measured data of material properties.

Key words:empirical correlation; impact energy; fracture toughness

中圖分類號：TQ050.4

文獻標志碼：A

文章編號：1000-3738(2015)12-0084-07