氣體介質(zhì)的非灰輻射計(jì)算研究
王扶輝,婁 春
(華中科技大學(xué)煤燃燒國(guó)家重點(diǎn)實(shí)驗(yàn)室,武漢 430074)
氣體介質(zhì)的非灰輻射計(jì)算研究
王扶輝,婁 春
(華中科技大學(xué)煤燃燒國(guó)家重點(diǎn)實(shí)驗(yàn)室,武漢 430074)
為得到更加精確的碳?xì)淙紵鹧娴妮椛溆?jì)算結(jié)果,采用將基于HITEMP光譜數(shù)據(jù)庫(kù)而建立的光譜模型——FSK模型與可準(zhǔn)確計(jì)算高方向分辨率輻射強(qiáng)度的DRESOR法相耦合的方式,對(duì)一維平板系統(tǒng)內(nèi)的CO2和H2O的混合氣體介質(zhì)的輻射情況在不同工況下展開計(jì)算,得到輻射強(qiáng)度及輻射熱流分布,并與其他方法進(jìn)行分析比較,從而檢驗(yàn)該方法的精確性及適用性。
介質(zhì)輻射;FSK模型;DRESOR法;k分布
0 引 言
介質(zhì)的輻射傳遞問題在諸如爐膛燃燒系統(tǒng)或大氣建模過程等場(chǎng)合中十分常見,近些年隨著能源問題的加劇,以全氧燃燒技術(shù)[1]為代表的節(jié)能技術(shù)的發(fā)展使得CO2和H2O的氣體輻射影響變得尤為重要。氣體輻射特性的計(jì)算有多種方法,其中逐線法(LBL)雖然保證了計(jì)算結(jié)果的高準(zhǔn)確度,但由于其巨大耗時(shí)的計(jì)算量,一般只將逐線計(jì)算法的結(jié)果作為檢驗(yàn)其他模型精確度和有效性的基準(zhǔn)解[2]。因此,我們需要得到一個(gè)計(jì)算量較少的高效計(jì)算模型,當(dāng)然,這種模型計(jì)算結(jié)果的精度可能會(huì)不及逐線法,但需要有著可觀的計(jì)算速度并在大部分工程應(yīng)用中可滿足我們所需要的精確度。文中所采用的FSK全光譜模型便是目前應(yīng)用較為普遍的光譜模型,該模型是由Modest[3-4]提出,其主要優(yōu)點(diǎn)為可與任意求解輻射傳遞方程的方法結(jié)合,而且只需對(duì)少量的光譜吸收系數(shù)進(jìn)行數(shù)值積分便可得到總的吸收系數(shù),大大提高了計(jì)算效率。
在伴隨著譜帶光譜模型向前發(fā)展的同時(shí),尋求準(zhǔn)確有效的求解輻射傳遞方程的方法也在一直進(jìn)行。經(jīng)過近些年的發(fā)展,已經(jīng)出現(xiàn)了多種求解方法,主要有:離散坐標(biāo)法(Discrete Ordinate Method)、區(qū)域法(Zonal)、球形諧波法(Spheric Harmonics)和蒙特卡洛法(Monte Carlo)等[5]。文中要采用的DRESOR法(Distributions of Ratios of Energy Scattered Or Reflected)最早是由周懷春課題組基于Monte Carlo 法提出的一種求解輻射傳遞方程的方法[6],其優(yōu)點(diǎn)在于能夠處理具有復(fù)雜幾何形狀的復(fù)雜輻射傳熱問題,同時(shí),該方法還能夠計(jì)算任意點(diǎn)高方向分辨率、高精度的輻射強(qiáng)度。
從以上對(duì)FSK模型以及DRESOR法的引入,我們可知FSK模型從計(jì)算效率、計(jì)算范圍以及應(yīng)用程度上都較其他模型有一定的優(yōu)勢(shì),而DRESOR法求解輻射方程的高方向分辨率、高精確性使得該方法較傳統(tǒng)的幾種方法來講優(yōu)點(diǎn)更明顯。所以將此兩者結(jié)合來計(jì)算輻射問題會(huì)得到相對(duì)較為精確的結(jié)果。文中將基于最新的Hitemp2010光譜數(shù)據(jù)庫(kù)[7][8]利用FSK模型結(jié)合DRESOR法和DO法來計(jì)算一維平板系統(tǒng)內(nèi)的氣體輻射情況并作比較。
1 FSK模型以及DRESOR法簡(jiǎn)述
1.1 FSK模型及DRESOR法
K分布的前提是普朗克函數(shù)在進(jìn)行K分布的光譜范圍內(nèi)基本保持不變,但是由式(1)可知在整個(gè)紅外光譜范圍即全譜帶內(nèi),普朗克函數(shù)并不是保持不變,它是溫度和波數(shù)的數(shù)。由于氣體輻射特性在整個(gè)光譜區(qū)間上間斷分布且變化劇烈,大小不同的吸收系數(shù)在相同的幾何長(zhǎng)度上的光學(xué)厚度不同,致使無法對(duì)其統(tǒng)一計(jì)算,所以吸收系數(shù)在光譜區(qū)間的劇烈化是處理氣體吸收的最大障礙。K分布模型的核心則是將劇烈變化的吸收系數(shù)重新排列,使其由原來的無規(guī)律形式變成平滑單調(diào)上升的函數(shù),對(duì)相同的吸收系數(shù)只需進(jìn)行一次輻射強(qiáng)度計(jì)算。這樣便會(huì)大大簡(jiǎn)化算法,所以全譜帶K分布模型就是要把K分布的思想應(yīng)用到全譜帶范圍內(nèi)。
(1)
因?yàn)樵谌V帶內(nèi),普朗克函數(shù)不再恒定不變,為了在全譜帶內(nèi)應(yīng)用K分布的思想,應(yīng)做如下處理,首先定義一個(gè)普朗克比例函數(shù):
(2)
顯然,i(T,0)=0,i(T,∞)=1,也就是說普朗克比例函數(shù)是單調(diào)遞增的,且0≤i≤1。接下來假定吸收系數(shù)對(duì)光譜和空間的依賴性可進(jìn)行分離,即所謂的“比例近似”:
κη(η,T,p,x)=κη(η)u,(T,p,x)
(3)
這種近似經(jīng)常應(yīng)用在介質(zhì)溫度和分壓不均勻的介質(zhì)當(dāng)中,且在大氣環(huán)境下的輻射傳熱計(jì)算中得到了比較精確的結(jié)果。
下面以透射率τ為例,對(duì)κη基于i進(jìn)行K分布,如下所示:
(4)
這里κ(Tref,gref)是在一個(gè)參考溫度Tref的情況下得到的K分布,它不再所溫度的變化而變化,也就是說這樣的處理方法把κ對(duì)溫度的依賴性全部集中到函數(shù)a當(dāng)中去了,也就是說,對(duì)于同一個(gè)介質(zhì)對(duì)象,選擇不同溫度的普朗克比例函數(shù),就有不同的k-g分布圖,并不改變介質(zhì)本身的輻射特性。
以上就是在全譜帶上進(jìn)行的K分布的過程,也就是全譜帶K分布模型,考慮的介質(zhì)僅限定在溫度和摩爾分?jǐn)?shù)不變的情況下。可以看到最終求解輻射傳遞方程我們只關(guān)注a函數(shù)和累積分布函數(shù)g。
對(duì)于DRESOR法求解一維RTE時(shí)[9],考慮發(fā)射、吸收、各向同性散射的平行平板介質(zhì),介質(zhì)的吸收系數(shù)為κa(τ),各項(xiàng)同性散射系數(shù)為κs(τ),溫度為T(τ),邊界為真空或者沒有入射輻射的冷黑體壁面。
向上和向下方向的輻射強(qiáng)度(即RTE的一般積分形式解)可寫成:
(5)
(6)
下面給出采用DRESOR法的計(jì)算式如下:
(7)
(8)
式中:
(9)
[Qe(τ″)/β]dτ′dτ″
(10)
(11)
(12)
上式的物理意義解釋如下:IR,1(τ,μ)表示總輻射強(qiáng)度IR(τ,μ)的直接部分,它來自于整個(gè)輻射傳遞系統(tǒng)在傳播路徑經(jīng)過吸收、散射后剩余的輻射。表示總輻射強(qiáng)度IR,2(τ,μ)表示總輻射強(qiáng)IR(τ,μ)的間接部分,它表示經(jīng)過介質(zhì)散射的間接部分(被壁面反射的部分在此不考慮),負(fù)方向上的輻射強(qiáng)度可類似得出。
1.2 FSK模型與DRESOR法耦合
以上分別介紹了FSK模型與DRESOR法的計(jì)算原理,而將兩者結(jié)合起來則是本文的關(guān)鍵所在。由FSK給出的k-g分布顯示g=0時(shí)得到k的最小值,在g=1時(shí)得到k的最大值,其實(shí)質(zhì)為將全光譜各個(gè)波段下的吸收系數(shù)進(jìn)行重排并劃分為一定的組數(shù)(文中采取將FSK中k-box的數(shù)目設(shè)置為500),然后依次將每組的吸收系數(shù)k與其所對(duì)應(yīng)的所占比例份額Δg由k-g分布給出。而對(duì)于DRESOR法來說,對(duì)于不同的吸收系數(shù)將得出不同的輻射強(qiáng)度值,所以在這種情況下將得到500組輻射強(qiáng)度值,為了求得總的輻射強(qiáng)度,我們基于k-g分布重新定義一個(gè)新的“譜線”概念,將此500組k、g值認(rèn)為是500組譜線所對(duì)應(yīng)的參數(shù),那么每條譜線的輻射強(qiáng)度定義為Ig,則總的輻射強(qiáng)度I就是對(duì)Ig在“全譜帶”即g從0到1上進(jìn)行積分。
(13)
這里Igi由DRESOR法依次計(jì)算得出,而Δgi=gi-gi-1,如此便可得到全光譜下的輻射強(qiáng)度值,通過輻射強(qiáng)度值進(jìn)而得到輻射熱流以及熱流梯度等。
2 算例分析
2.1 一維對(duì)象
文中計(jì)算對(duì)象為一維平行平板系統(tǒng),板間距為1 m,兩板之間劃分為N=100個(gè)網(wǎng)格,離散方向數(shù)為M=180;邊界為冷黑邊界,介質(zhì)為CO2、H2O與N2的混合氣體,溫度為T=2 000 K,壓力為P=1 bar,N2不參與輻射。
2.2 主要波段處的吸收系數(shù)
這里所說的主要光帶即CO2與H2O共同的主要光帶,有兩處:2.7 μm和15 μm附近[10],本算例選擇了上述波長(zhǎng)所對(duì)應(yīng)的以下兩個(gè)波數(shù)范圍:500 cm-1≤η≤800 cm-1和3 500 cm-2≤η≤3 800 cm-1。 溫度壓力條件:T=2 000 K,P=1 bar。
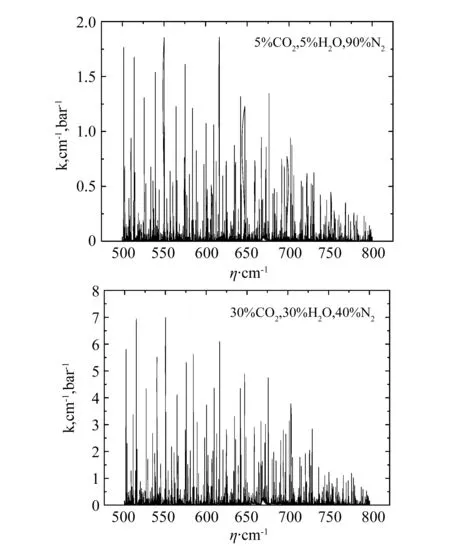
圖1 不同濃度下混合氣體在波長(zhǎng)為15 μm附近處的吸收系數(shù)分布

圖2 不同濃度下混合氣體在波長(zhǎng)為2.7 μm附近處的吸收系數(shù)分布
從以上的計(jì)算結(jié)果中可以看出隨著CO2與H2O所占?xì)怏w份額增大,即濃度變大,所得吸收系數(shù)也隨之增大,可以看到對(duì)于同一波段來說,吸收系數(shù)的相對(duì)大小趨勢(shì)(圖形的形狀)是基本不變化的,隨濃度增大吸收系數(shù)的值整體增大了而已。
2.3 k分布以及a分布
Modest等人曾計(jì)算了介質(zhì)為H2O時(shí)不同普朗克溫度下的k-g分布[11],下圖給出了CO2與H2O的混合介質(zhì)在參考溫度為2 000 K時(shí)不同普朗克溫度下所對(duì)應(yīng)的k-g分布。可以看到對(duì)不同溫度的普朗克比例函數(shù)g,即有著不同的k-g分布,且為平滑單調(diào)遞增曲線滿足k思想的特點(diǎn),這一點(diǎn)由g和k的物理關(guān)系很容易理解。
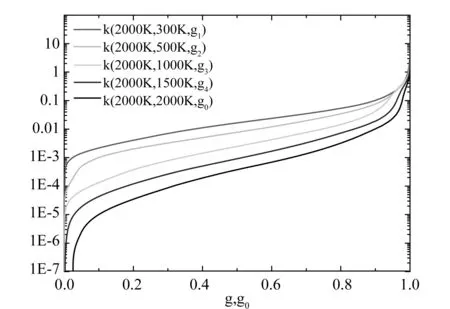
圖3 30%CO2,30%H2O時(shí)不同溫度下的k-g分布
以下兩圖為介質(zhì)溫度分別為300 K和1 500 K時(shí)的a函數(shù)的值,即k對(duì)溫度的依賴函數(shù)。由于參考溫度為2 000 K,可見當(dāng)介質(zhì)溫度跟參考溫度相差得越大,a函數(shù)的值則越大,符合a函數(shù)的這一特點(diǎn)。
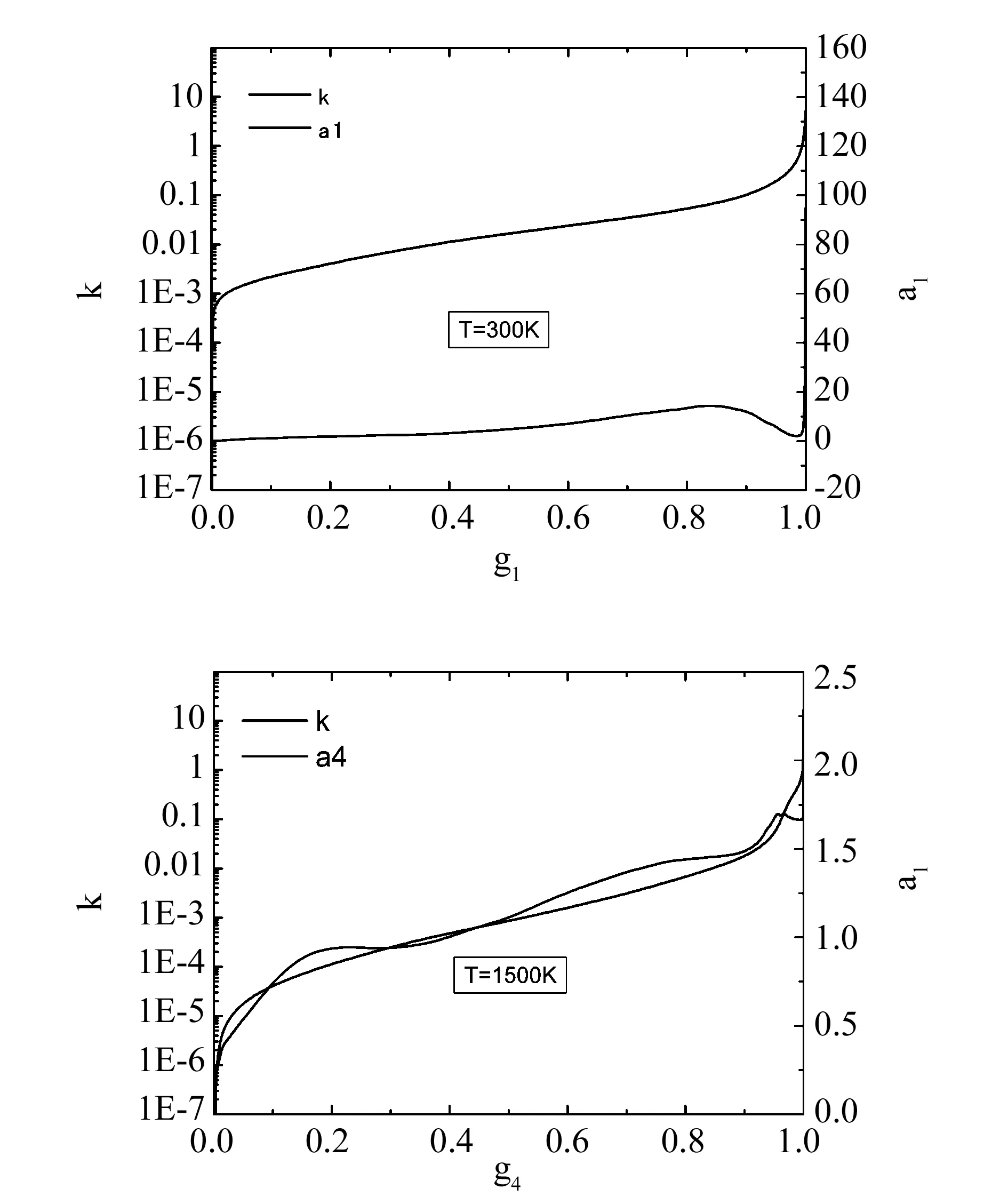
圖4 不同介質(zhì)溫度時(shí)的a-g及k-g分布
2.4 輻射強(qiáng)度及熱流
仍然考慮一維平行平板系統(tǒng)并將介質(zhì)成分設(shè)定為10%CO2、20%H2O與70%N2的混合氣體,溫度壓力不變,這里將DRESOR法的計(jì)算結(jié)果與DO法所得結(jié)果進(jìn)行了比較。
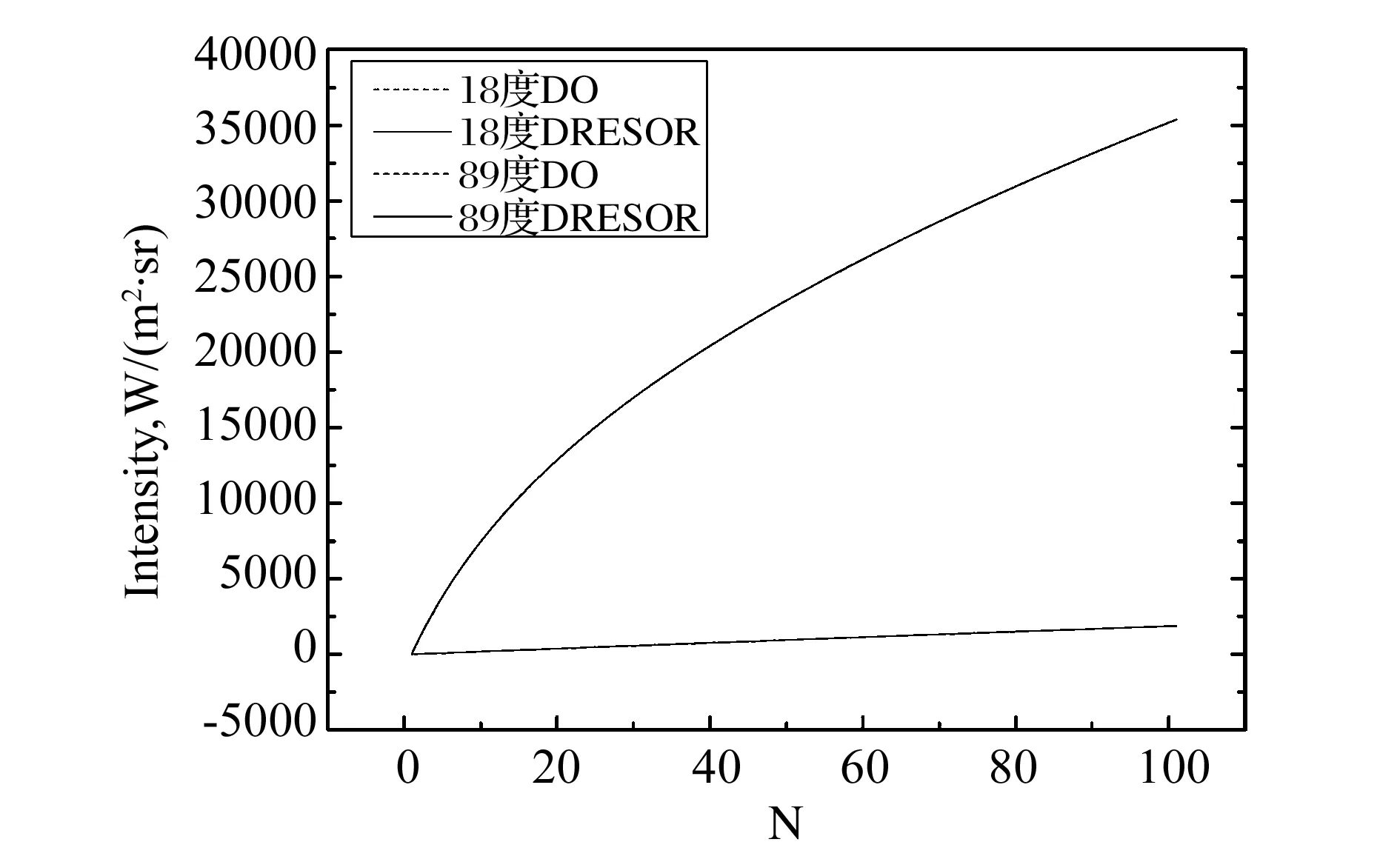
圖5 兩個(gè)角度方向上的輻射強(qiáng)度比較
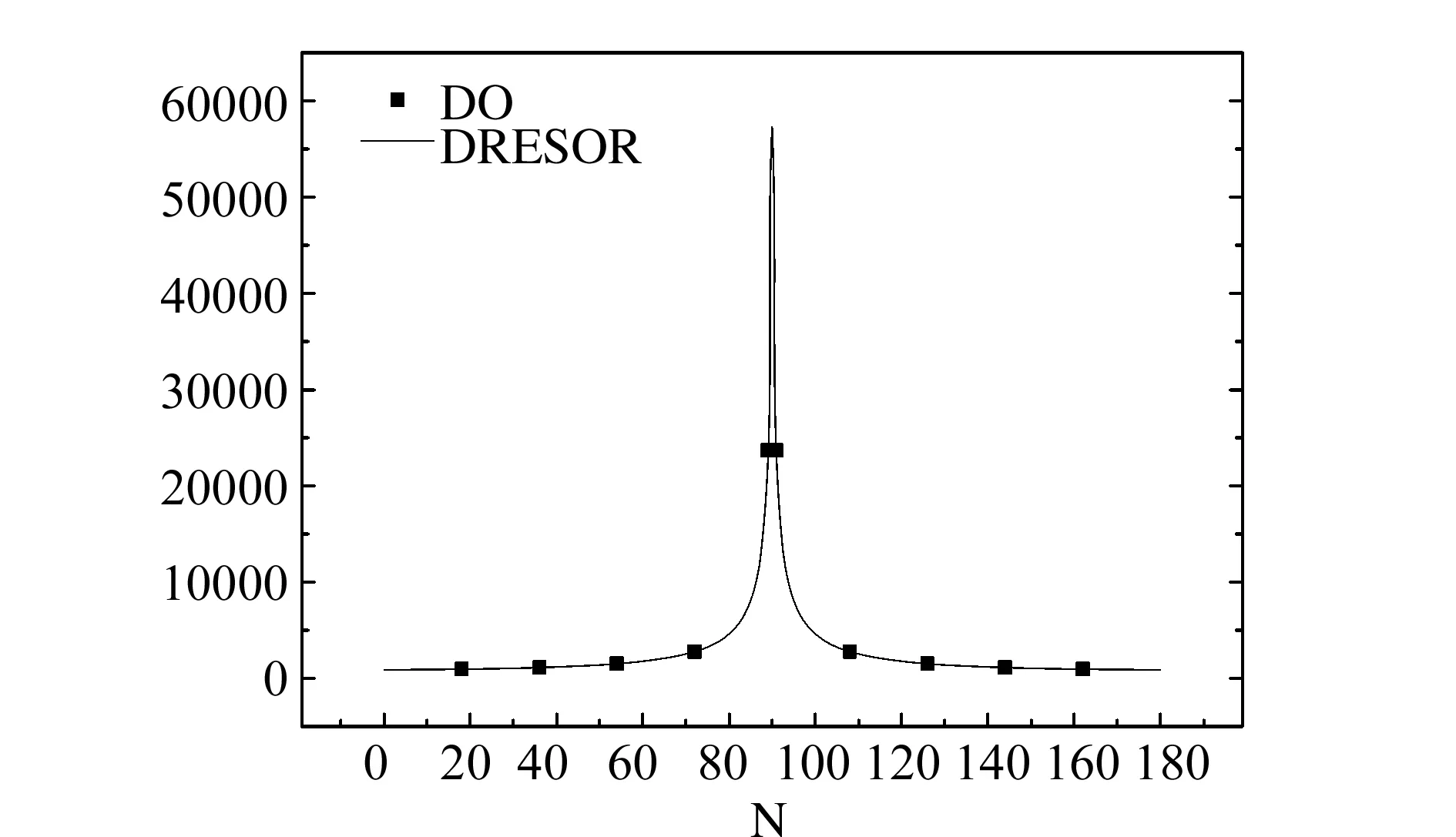
圖6 中間節(jié)點(diǎn)處的輻射強(qiáng)度對(duì)比
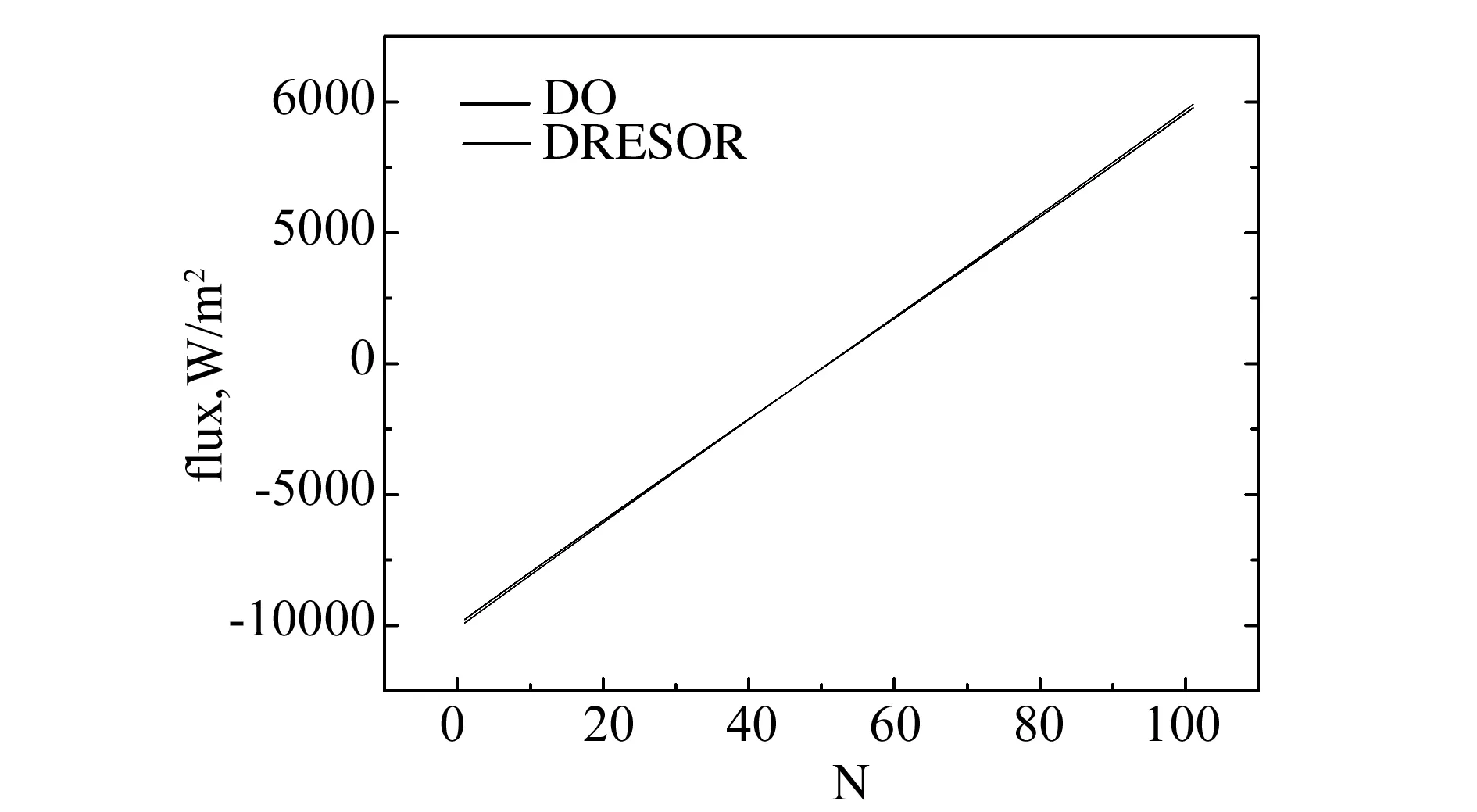
圖7 輻射熱流對(duì)比
以上給出了計(jì)算結(jié)果比較,現(xiàn)給出FSK模型與逐線法的計(jì)算誤差比較以及DRESOR法的計(jì)算誤差與計(jì)算效率。

表1 FSK與LBL的誤差比較
將DRESOR法計(jì)算所得輻射強(qiáng)度代入輻射傳遞方程的兩邊,可得出其計(jì)算誤差,現(xiàn)取下邊界的輻射強(qiáng)度為例。

表2 DRESOR法的驗(yàn)證誤差比較

表3 DRESOR法與DO法計(jì)算效率比較
計(jì)算時(shí)間上可得知DRESOR法遠(yuǎn)遠(yuǎn)大于DO法,這是由于其給出了高方向分辨率的輻射強(qiáng)度,所以其計(jì)算效率相對(duì)較低。
2.5 熱流梯度
分別用DO法和DRESOR法從空氣燃燒和富氧燃燒兩種燃燒情況下計(jì)算介質(zhì)的輻射熱流梯度,其中兩種燃燒情況下的氣體份額如表4所示,熱流梯度值由圖8給出。
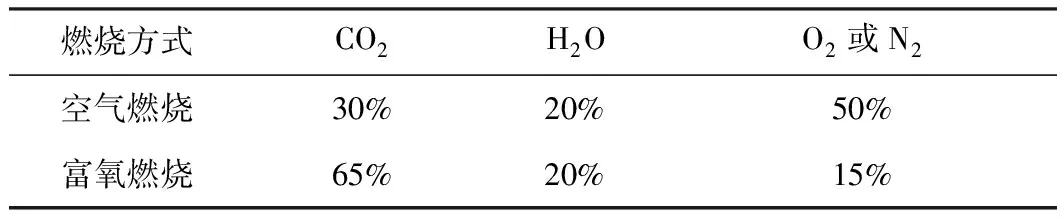
表4 兩種燃燒方式下的氣體份額
以上我們可以看到在兩種燃燒方式下,DO法與DRESOR法具有較為一致的結(jié)果,這也再一次說明了該方法的精確性以及實(shí)用性。但是在空氣燃燒方式下兩種方法的計(jì)算結(jié)果有一定的差異,特別是在靠?jī)蛇吂?jié)點(diǎn)處,DRESOR法的熱流梯度值要稍高于DO法的,這是由于在靠?jī)蛇吂?jié)點(diǎn)處,兩種方法所計(jì)算得到的熱流值誤差所引起的,這里用熱流梯度來進(jìn)行比較分析是為了將該誤差放大以此說明兩種方法的本身計(jì)算誤差。而這種誤差是由兩種方法的計(jì)算原理不同所產(chǎn)生的。
3 結(jié)束語(yǔ)
文中首先基于HITEMP光譜數(shù)據(jù)庫(kù)利用K分布重排思想對(duì)CO2和H2O的混合氣體的吸收系數(shù)進(jìn)行了計(jì)算,接著分別用DRESOR法和DO法與FSK模型結(jié)合計(jì)算了簡(jiǎn)單一維平板系統(tǒng)中不同工況下的氣體輻射強(qiáng)度、輻射熱流以及輻射梯度并進(jìn)行了對(duì)比,結(jié)果顯示兩種方法在計(jì)算空間各點(diǎn)的輻射熱流和各點(diǎn)在DO法所選方向上的輻射強(qiáng)度以及輻射梯度均具有很好的吻合性,這就說明兩種方法在求解該問題時(shí)具有一致的結(jié)果。同時(shí)表明用FSK模型結(jié)合DRESOR法求解輻射問題具有很高的精確性以及廣泛的實(shí)用性。
文中對(duì)FSK模型與DRESOR法的結(jié)合只是在較為簡(jiǎn)單的一維系統(tǒng)中進(jìn)行了計(jì)算,主要是驗(yàn)證了該方法的可行性并體現(xiàn)該方法的一些特點(diǎn),可以看到在各向同性散射下DRESOR法高空間方向分辨的優(yōu)勢(shì)未能明顯地體現(xiàn)出來,而且計(jì)算效率相對(duì)較低,這對(duì)于輻射問題的計(jì)算來說還遠(yuǎn)遠(yuǎn)不夠。所以在后續(xù)工作中計(jì)劃考慮各向異性散射并嘗試運(yùn)用由王貴華提出的ES-DRESOR法[12]來提高計(jì)算效率,以便更加方便準(zhǔn)確地來計(jì)算相關(guān)輻射問題。
[1] 朱興營(yíng),閆金山,陳志偉,等.全氧燃燒技術(shù)在氧化鋁回轉(zhuǎn)窯上的應(yīng)用分析[J].應(yīng)用能源技術(shù),2013,9(10):38-42.
[2] 尹雪梅,劉林華.高溫氣體輻射特性計(jì)算模型[J].熱能動(dòng)力工程,2007,22(5):473-479.
[3] Modest MF,Zhang H.The full-spectrum correlated-k distribution for thermal radiation from molecular gas-particle mixtures [J].Journal of Heat Transfer, 2002,124 (1):30-38.
[4] Modest MF.Narrow-band and full-spectrum k-distributions for radiative heat transfer-correlated-k vs. scaling approximation [J].Journal of Heat Transfer, 2003, 76 (1):69-83.
[5] Modest MF.Radiative Heat Transfer [M], Second edition. New York: Academic Press, 2003.
[6] Zhou HC, Chen DL, Cheng Q.A new way to calculate radiative intensity and solve radiative transfer equation through using the Monte Carlo Method[J].Journal of Quantitative Spectroscopy & Radiative Transfer.2004, 83 (4): 459-481.
[7] Rothman LS,Gordon IE,Barber RJ,et al.HITEMP,the high-temperature molecular spectroscopic database[J].Journal of Quantitative Spectroscopy & Radiative Transfer,2010, 111 (15): 2139-2150.
[8] Bailey J. A comparison of water vapor line parameters for modeling the Venus deep atmosphere, Icarus, 2009, 201(4):44-53.
[9] 周懷春,何 誠(chéng),程 強(qiáng).DRESOR法求一維各向異性散射內(nèi)的輻射傳遞[J].華中科技大學(xué)學(xué)報(bào):自然科學(xué)版.2006, 34 (1):17-20.
[10] 楊世銘,陶文銓.傳熱學(xué),第四版[M].北京:高等教育出版社,2006.419-421.
[11] Modest MF, Singh V. Engineering correlations for full spectrum k-distributions of H2O from the HITEMP spectroscopic databank [J].Journal of Heat Transfer,2005, 93 (1) :263-271.
[12] 王貴華.一維各向同性散射系統(tǒng)內(nèi)輻射傳遞分析的ES-DRESOR法[D].華中科技大學(xué),2012.
Research on Non-gray Radiation Calculation for Gas Medium
WANG Fu-hui, LOU Chun
(State Key Laboratory of Coal Combustion. Huazhong University of Science and Technology, Wuhan 430074, China)
In order to obtain more precision results of radiation calculation. A way of correct coupling between the following model and method is adopted. The FSK model, a spectral model is established based on HITEMP spectral database. The DRESOR method, which can calculate the radiation intensity with high direction resolution accurately. Carry out the results of the radiation for mixed media of CO2and H2O in the one dimensional flat system under different cases. After obtain the radiation intensity and radiation heat flux distribution, analyzing and comparing with other method thus will test the accuracy and applicability of the method.
Media radiation; FSK model; DRESOR method; K-distribution
2014-12-20
2015-01-09
國(guó)家自然科學(xué)基金項(xiàng)目(Nos.51176059, 51025622, 51021065)資助
王扶輝(1991-),男,甘肅景泰人,華中科技大學(xué)熱能工程專業(yè)在讀碩士研究生,研究方向?yàn)榻橘|(zhì)輻射計(jì)算。
10.3969/j.issn.1009-3230.2015.02.002
TK223.2
B
1009-3230(2015)02-0006-06

