帶有退火和雜交變異思想的改進粒子群算法

黃煒霖 ，劉建軍 ，張 明 ，呂照明 ，伍 建

1.中國石油大學（北京）理學院，北京 102249

2.中國石油大學（北京）油氣資源與探測國家重點實驗室，北京 102249

3.中國石油大學（北京）CNPC物探重點實驗室，北京 102249

1 引言

粒子群優化算法（PSO）是由Kennedy和Eberhart在1995年提出的一種新型進化計算方法[1-2]。PSO算法原理簡單且易實現，迭代運算的參數少，具有較快的收斂速度。近年來的研究表明，該算法在許多優化問題中表現優秀，已被成功應用到參數辨識、模式識別、網絡優化等許多領域[3-6]。

但是，基本PSO算法在求解復雜函數優化問題時，求解過程中易出現“早熟現象”，進而無法找到全局最優解，同時搜索的精度不高。針對算法的這些不足，很多學者將其他優化算法思想融入PSO算法中，Lovbjerg等人提出了帶交叉算子的PSO算法[7]；Liu等人將混沌算法的思想引入PSO算法中[8]；Holden等人混合PSO算法和蟻群算法[9]等等[10-16]。為了解決PSO應用中出現的早熟現象，本文首先應用信息熵算法產生分布更為均勻的初始群體，然后基于模擬退火算法中依概率接受劣解，和遺傳算法中雜交變異產生新解的思想，提出了粒子群算法的一種新改進算法。

2 基本粒子群算法

PSO優化算法將待優化的參數組合成群體，再利用個體（粒子）的適應度使其向好的區域移動，每個粒子代表問題的一個可能解，每個粒子具有位置和速度兩個特征[1-2]。在D維搜索空間中，第i個粒子的位置可以表示成Xi，其速度表示成Vi，粒子位置坐標對應的目標函數值即可作為該粒子的適應度，算法依據適應度來衡量粒子的優劣。算法首先初始化一群隨機粒子，然后通過迭代找到最優解。在每次迭代中，粒子的更新是通過跟蹤兩個“極值”：一個是粒子本身經歷過的最優解，即個體極值pbesti；另一個是整個粒子群經歷過的最優解，即全局極值gbest，最后輸出的gbest就是算法得到的最優解。第i個粒子從第k代進化到第k+1代時，根據下面兩個公式更新速度與位置：

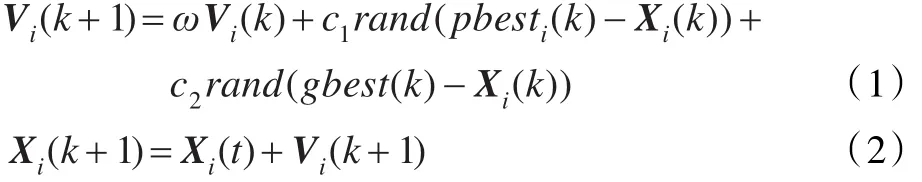
其中，ω為慣性權重，其作用是維護全局和局部搜索能力的平衡；c1和c2為加速因子，作用是控制粒子向pbesti和gbest移動的速度大小；rand為[0，1]范圍內的隨機數。

粒子群優化算法具有結構簡單，運行速度快的優點。在算法搜索過程中，某粒子發現一個當前最優位置，其他粒子便會迅速向其靠攏。但是，如果該最優位置為一局部最優點時，算法很容易陷入局部最優，粒子群就無法在解空間內重新搜索，出現了所謂的早熟收斂現象。

3 基于信息熵控制初始群體的生成

若初始群體沒有較均勻的分布在解空間，那么群體的多樣性將降低，導致算法全局搜索能力減弱。對此應用信息熵來提高初始群體的多樣性[17-18]。

在信息論中，熵通常也稱做信息熵或Shannon熵，它主要采用數值形式表達隨機變量取值的不確定性程度，或一個系統的混亂性、遍歷性、隨機性[19-21]。設初始群體由N個D維個體組成，并用X=(X1,X2,…,XD)來表示（每個分量為N維列向量），則第j維分量的信息熵Hj表示為：

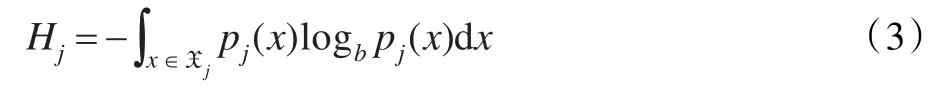
其中，pj(x)為隨機變量Xj的概率密度函數，Xj為第j維分量的取值范圍。

整個系統的信息熵H表示為：

其中，Qj為信息熵確定的權重。

對于概率密度函數，采取高斯核函數方法[22-23]來近似估計：

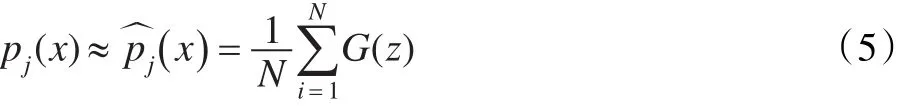
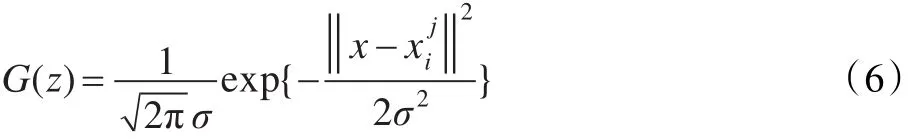
其中，為第j維分量的第i個值，σ為核函數的寬度。

由式（4）可知，熵值H越大，群體多樣性越好，即個體間差異越大，相反熵值H越小，群體多樣性越低，即個體間差異越小，當熵值H為零時，個體間無差異。因此，可以用熵值H來控制群體的生成，生成多樣性較好、遍歷性較高的初始群體，如圖1所示。

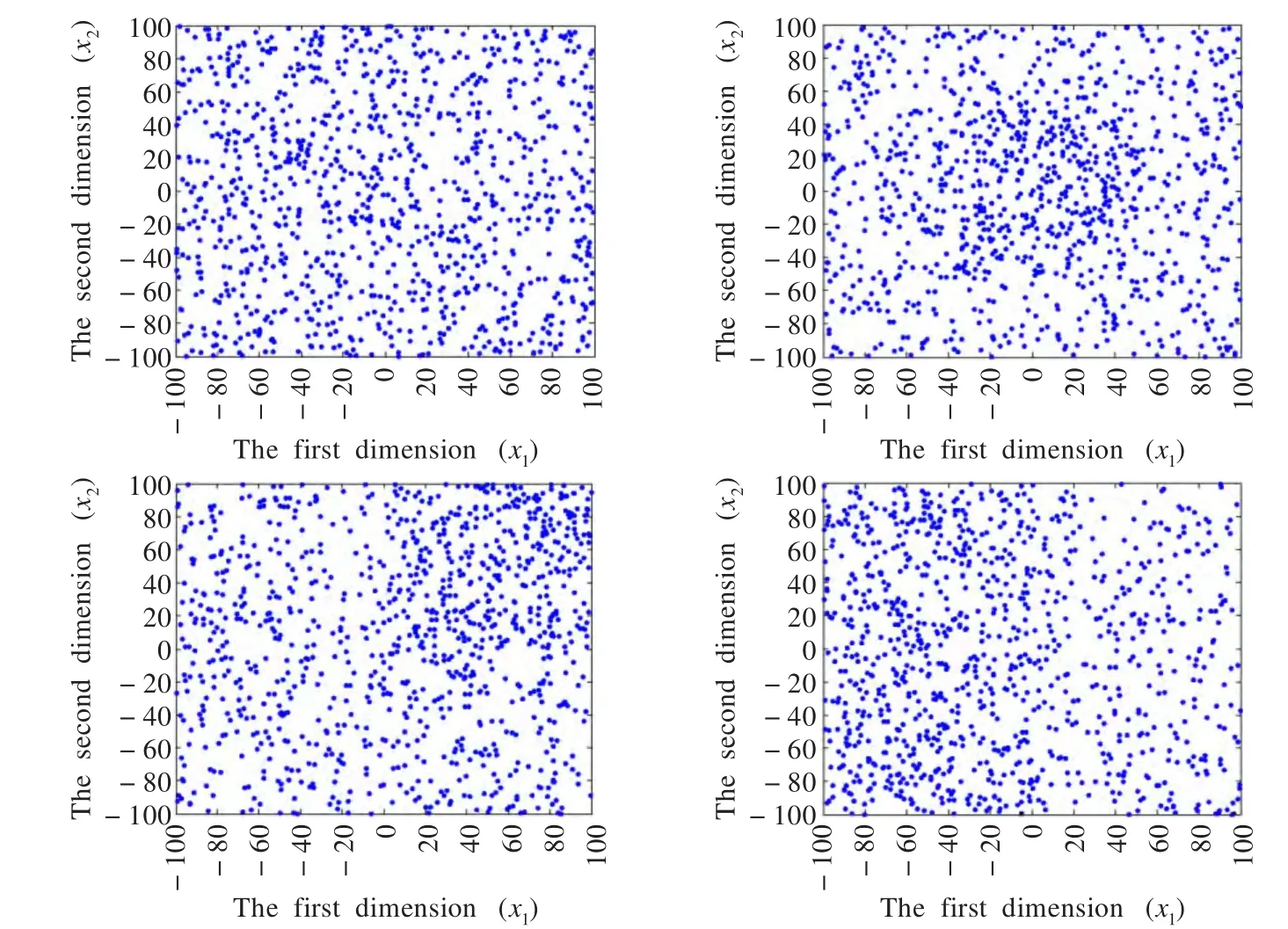
圖1 不同熵值H對應的初始種群分布

由于混沌序列具有混沌運動的遍歷性、隨機性和規律性等特點，能在一定范圍內按自身的規律不重復地遍歷所有狀態，所以很多學者用混沌映射來生成初始群體[24-25]。混沌模型有很多，最常用的是logistic映射，即：

其中，n=0,1,…，0≤y(n)≤1，u是控制參量，當u=4時，上述系統處于完全混沌狀態。

由于logistic映射生成的粒子分布在區間兩頭的概率遠大于中間，而中間分布較均勻，所以這里只取落在區間[0.1，0.9]里面粒子，舍棄其他粒子。

4 帶有模擬退火和雜交變異思想的粒子群算法4.1 雜交變異思想

遺傳算法中雜交算子能使個體間交換信息，而變異算子能使某些個體發生基因突變，使個體具有更大的遍歷性[26-27]。本文借鑒這個思想，通過雜交和變異來產生多樣性更好的后代。

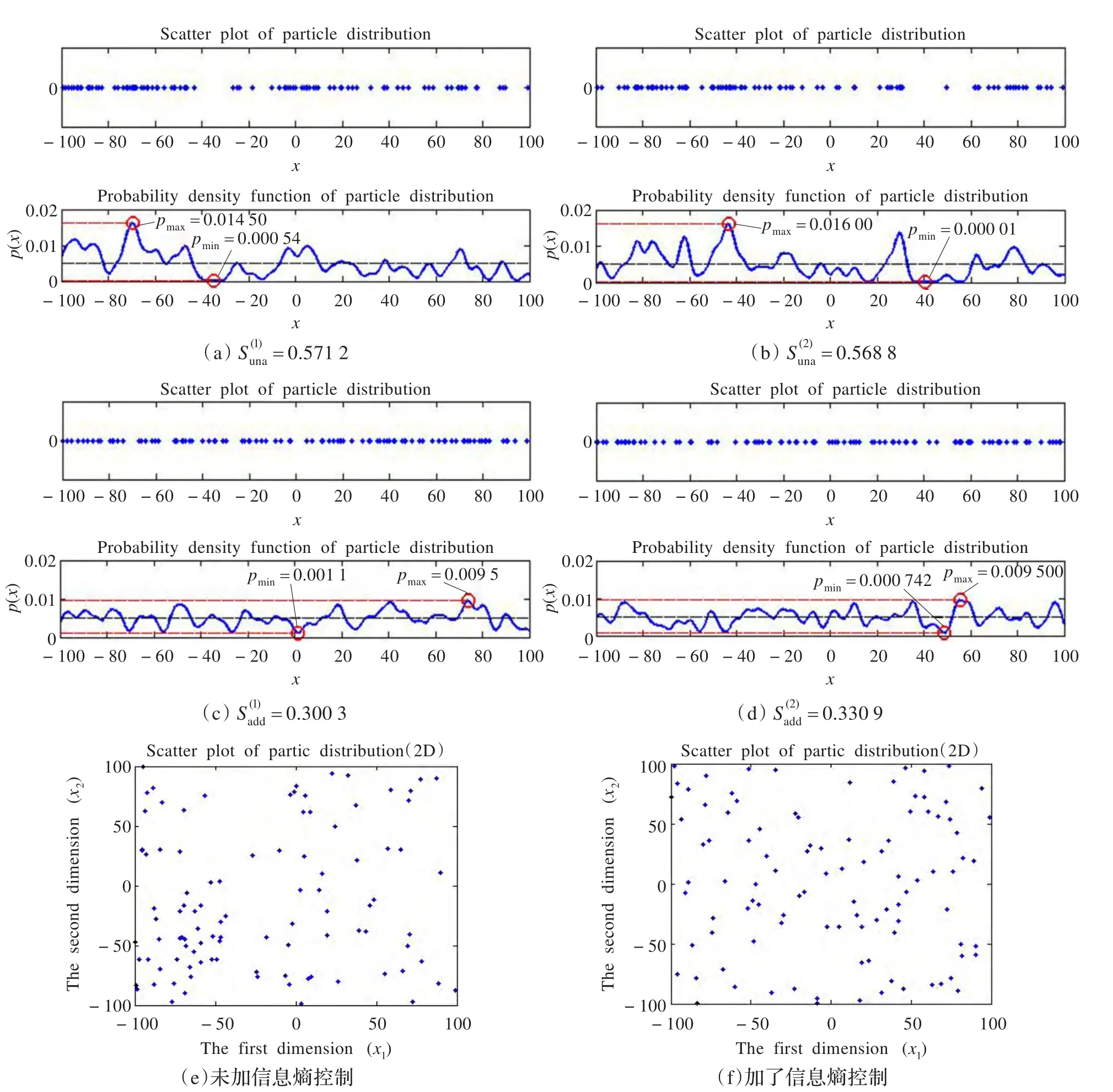
圖2 二維粒子分布和每維上的分布情況比較（100個）

4.1.1 雜交

在PSO算法迭代中，選取一定數目的粒子放入雜交池中，池中的粒子隨機進行雜交，然后產生同樣數目的子代粒子（child），再用子代粒子替換父代粒子（parent）。子代粒子由父代粒子算術交叉得到：

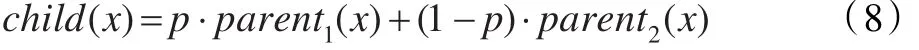
其中，p是0到1之間的隨機數。

4.1.2 變異

在PSO算法迭代中，以一小概率μ選取粒子，并隨機選取其某一維或者幾維，將它的值改變，改變的值為搜索范圍內的隨機數。這個概率μ可以是固定的，也可以是以某種方式下降的。

雜交和變異的操作，目的是增加群體的多樣性，幫助算法跳出局部最優，防止算法“早熟”。

4.2 退火思想

借鑒模擬退火算法搜索過程中具有概率突跳的能力，且不但接受好解，還以一定的概率接受劣解，同時這種概率受到溫度參數的控制[27-28]。本文對其進行修改，將這種思想融合到粒子群算法中。在4.1.1小節所述的雜交操作中，是以這樣的步驟選取粒子放入雜交池中：

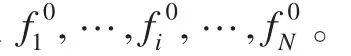
步驟2計算初始溫度：

其中fmax、fmin分別表示最大的適應值和最小的適應值。

步驟3計算雜交比例：

其中λ為取值在0到1之間的比例系數，作用是控制比例大小，k為當前迭代步數，M為最大迭代步數。

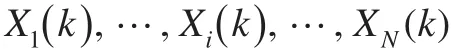
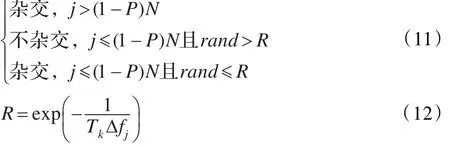
其中rand表示0到1之間的一個隨機數，Δfj表示第j個粒子的適應值與全局最優點適應值之差。

步驟5降溫：

其中μ為降溫系數，作用是控制溫度下降的快慢。

上述過程可以這樣理解：當j＞(1-P)N，就進行雜交，相當于模擬退火算法中接受收好解的過程，這里是接受劣解進入雜交池；當j≤(1-P)N，就依概率R來判斷是否雜交，相當于模擬退火算法中依概率接受劣解，這里是依概率接受好解進入雜交池，且粒子越好，進入雜交池的可能性就越小。

上述操作的目的有二：一是加速算法的收斂速度，越到迭代后期，雜交比例P和接受好解進入雜交池的概率R越小；二是使算法具有突跳能力，能有效的跳出局部極小點。

4.3 算法步驟

步驟1給定一個臨界熵值H0，隨機產生初始群體并按式（3）、（4）、（5）、（6）計算他的熵值H，若H＞H0則隨機初始化該初始群體的速度，轉步驟2；否則重新隨機產生初始群體直到滿足H＞H0為止。

步驟2評價每個粒子的適應度，將當前各粒子的位置和適應值存儲在各粒子的pbesti中，將所有pbesti中適應值最優個體的位置和適應值存儲在gbest中。

步驟3按式（9）計算初始溫度T0。

步驟4按式（1），（2）更新每個粒子的速度和位置。

步驟5對粒子群體進行變異操作。

步驟6計算每個粒子的目標函數值，按式（10）、（11）、（12）計算出放入雜交池的粒子，以及保留的粒子。

步驟7將步驟6中雜交池中的粒子按式（8）隨機進行雜交，然后產生同樣數目的子代粒子，再用子代粒子替換父代粒子。

步驟8更新每個粒子的pbesti以及群體的gbest。

步驟9若滿足停止條件（精度或者迭代次數等），搜索停止，輸出結果；否則轉步驟10。

步驟10按式（12）進行降溫操作，轉步驟4。

5 仿真實驗

下面通過4個典型函數優化問題（求解最小值）來測試本文提出的算法的性能。

測試函數1，Sphere函數：

其中-100＜xi＜100，最優狀態和最優值為：

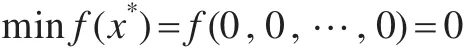
測試函數2，Rastrigin函數：

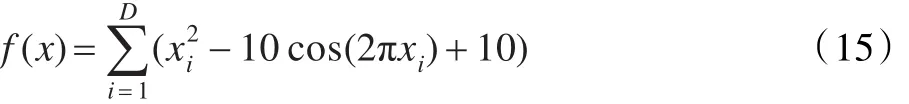
其中-5.12＜xi＜5.12，最優狀態和最優值為：

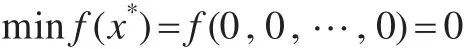
測試函數3，Ackley函數：

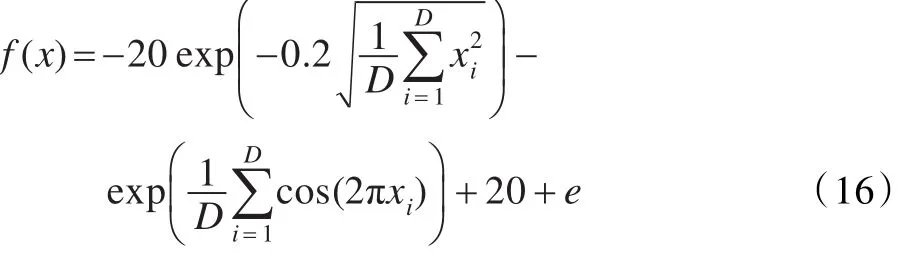
其中-32＜xi＜32，最優狀態和最優值為：

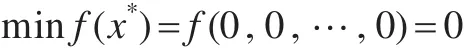
測試函數4，Griewank函數：

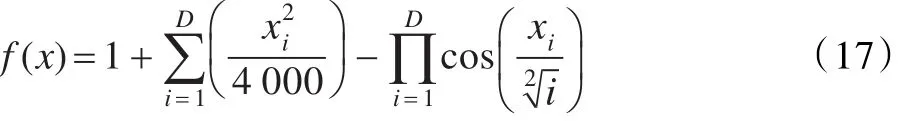
其中-600＜xi＜600，最優狀態和最優值為：

對每個測試函數，分別采用標準粒子群算法（PSO）、遺傳粒子群算法（GAPSO）[29-30]和本文所提出的帶有模擬退火和雜交變異思想的粒子群算法（SAHMPSO）進行測試。

為了保證實驗的客觀性，對于基本參數的設定，3種算法均為：種群大小N為40；函數維數D分別為10、20、30；加速因子c1=c2=1.4；慣性權重ω=0.65；最大迭代次數為5 000。對于每個測試函數，每種算法運行100遍，其中Avg表示運行100次的結果的平均值，Var表示運行100次的結果的方差，Best表示運行100次的結果的最小值。運算結果如表1所示。

為了分析算法的收斂性能，將3種算法在4個測試函數上的最優值best記錄下來，以橫坐標為迭代次數，縱坐標為函數的對數值，作出圖形如圖3所示（僅展示10維情況）。

Sphere函數為連續的單峰函數，自變量之間互相獨立，Rastrigin、Ackley、Griewank這3個函數為復雜的非線性多峰函數，存在大量局部極小值。從表1可以看到，本文提出的算法，無論是在搜索精度還是在穩定性都明顯的高于其他兩種算法。

Sphere函數常用于測試算法的收斂速度，Rastrigin函數常用于測試算法的全局搜索性能。由圖3（a）和（b）看到，在迭代早期，3種算法的收斂速度基本相當，而在迭代的中后期，由于PSO算法的“早熟”使得算法停滯不前，陷入了局部極小，而GASPSO算法雖然找到了比PSO算法更好的解，但很快也陷入了局部極小。而SAHMPSO算法由于雜交，變異操作，在保持收斂速度的同時，大大地加強了抗“早熟”的能力。

Ackley函數常用于測試算法跳出局部極值的能力。由圖3（c）可以看到，PSO算法和GASPSO算法很快就陷入局部極值難以跳出，而SAHMPSO算法能一直保持著一個較快的速度下降，即使陷入局部極值，在若干次迭代后仍可跳出。

Griewank函數常用于測試算法對全局與局部搜索能力的平衡性能。由于本文算法融入了退火的思想，使得算法在兼顧局部搜索能力的同時，在迭代后期加快全局收斂速度，由圖3（d）可以看到，PSO算法同樣是在迭代次數不到100的時候就已經停滯不前了，而SAHMPSO算法在迭代前期保持了種群較大的多樣性，強化了算法的全局搜索能力，在迭代后期降低種群的多樣性，加快收斂，強化了算法的快速下降搜索能力。而信息熵控制的方法產生了均勻性良好的初始群體，加強了群體的多樣性，是算法的較高收斂性能的基礎。

6 結論

本文提出的改進算法中，利用信息熵控制生成初始群體，保證了初始群體的多樣性，為后續進化提供了基礎。改進算法中融入了模擬退火算法中的退火方法和遺傳算法中的雜交、變異算子，使得算法不僅保持了PSO算法前期函數值的快速下降性，還克服了原算法的“早熟”缺點，從而使算法的搜索性能得到很大的提高。通過數值實驗可以發現，本文的改進算法在抗“早熟”、搜索精度和穩定性方面均優于PSO及GAPSO，本文算法可進一步應用到實際問題中。

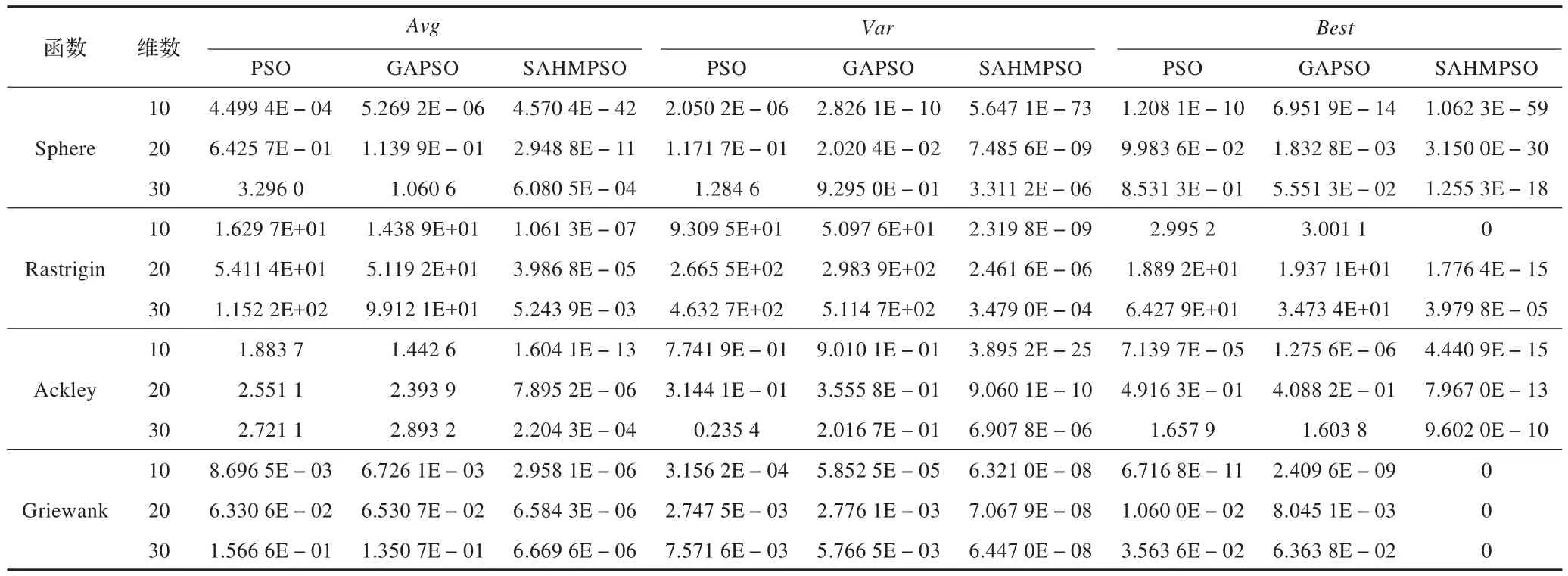
表1 3種算法針對4個函數在10、20和30維下的實驗結果（運行100次）

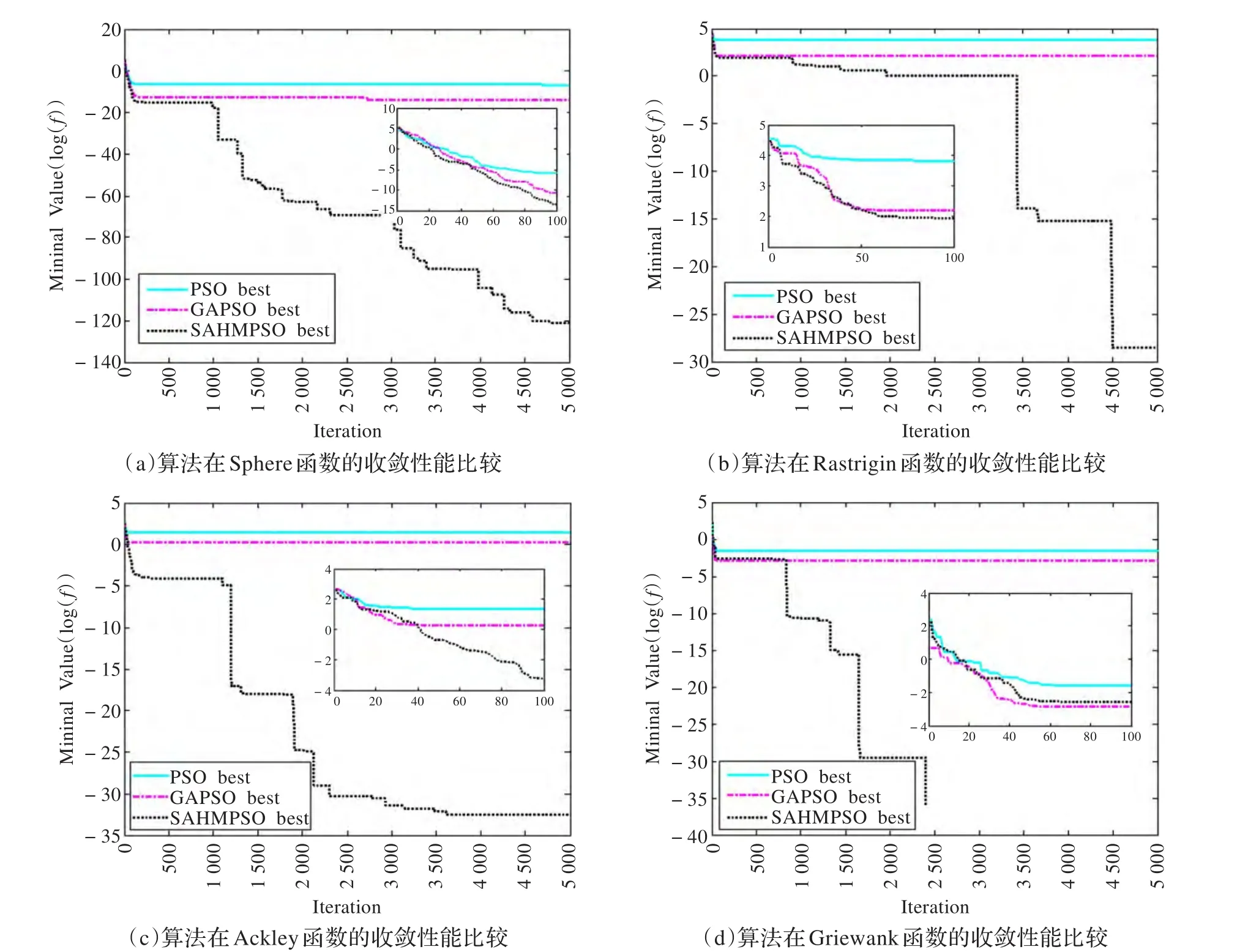
圖3 3種算法優化4個函數的收斂性能比較（小圖為前100步的迭代情況放大）

[1]Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proc of the 1st IEEE International Conference on Neural Networks，Perth，Australia，1995：1942-1948.

[2]Eberhart R C，Kennedy J.A new optimizer using particle swarm theory[C]//Proc of 6th Int Symp Micro Machine and Human Science，Nagoya，Japan，1995：39-43.

[3]戴運桃.粒子群優化算法研究及其在船舶運動參數辨識中的應用[D].哈爾濱：哈爾濱工程大學，2010.

[4]Yoshida H，Kawata K，Fukuyama Y，et al.A particle swarm optimization for reactive power and voltage control considering voltage security assessment[J].IEEE Transactions on Power Systems，2001，15（4）：1232-1239.

[5]Sousa T，Silva A，Neves A.Particle swarm based data mining algorithms for classification tasks[J].Parallel Computing，2004，30（5/6）：767-783.

[6]He Z，Wei C，Yang L，et al.Extracting rules from fuzzy neural network by particle swarm optimization[C]//Proceedings of IEEE Congress on Evolutionary Computation，Anchorage，Alaska，USA，1998.

[7]Lovbjerg M，Rasmussen T K，Krink T.Hybrid particle swarm optimizer with breeding and subpopulation[C]//Proceedings of Genetic and Evolutionary Computation Conf.San Francisco：Morgan Kaufmann Publishers Inc，2001：469-476.

[8]Liu Bo，Wang Ling，Jin Yihui，et a1.Improved particle swann optimization combined with chaos[J].Chaos，Solitons and Fractals，2005，25（5）：1261-1271.

[9]Holden N，Freitas A A.Hybrid particle swarm，ant colony algorithm for the classification of hierarchical biological data[C]//Proc of the IEEE Swarm Intelligence Symposium，Delhi，India，2005：100-107.

[10]胥小波，鄭康鋒，李丹，等.新的混沌粒子群優化算法[J].通信學報，2012（1）：24-30.

[11]李季，孫秀霞，李士波，等.基于遺傳交叉因子的改進粒子群優化算法[J].計算機工程，2008（2）：181-183.

[12]楊俊杰，周建中，喻菁，等.基于混沌搜索的粒子群優化算法[J].計算機工程與應用，2005，41（16）：69-71.

[13]Kiel R T，Thiemo K.Improved hidden Markov model training for multiples equence alignment hybrid[J].Bio-systems，2003，72（1/2）：5-17.

[14]Ji M J，Tang H W.Application of chaos in simulated annealing[J].Chaos，Solitons and Fractals，2004，21：933-941.

[15]張頂學.遺傳算法與粒子群算法的改進及應用[D].武漢：華中科技大學，2007.

[16]潘昊，侯清蘭.基于粒子群優化算法的BP網絡學習研究[J].計算機工程與應用，2006，42（16）：41-43.

[17]Chun J，Kim M.Shape optimization of electromagnetic devices using immune algorithm[J].IEEE Trans on Magnetics，1997，33（3）：1876-1879.

[18]袁曉輝，袁艷斌，王乘，等.一種新型的自適應混沌遺傳算法[J].電子學報，2006（4）：708-712.

[19]Cover T M，Thomas J A.Elements of information theory[M].New York：Wiley，1991.

[20]Cover T M，Thomas J A.信息論基礎[M].阮吉壽，張華，譯.北京：機械工業出版社，2005：9-28.

[21]張妍，楊志峰，何孟常，等.基于信息熵的城市生態系統演化分析[J].環境科學學報，2005（8）：1127-1134.

[22]Parzen E.On estimation of a probability density funcion and mode[J].Annals of Math Statistics，1962，33：1065-1076.

[23]Beirlant J，Dudewicz E J，Gyorfi L，et al.Nonparametric entropy estimation：An overview[J].International Journal of the Mathematical Statistics Sciences，1997，6：17-39.

[24]Tavazoei M S，Haeri M.An optimization algorithm based on chaotic behaviorand fractalnature[J].Journalof Computational and Applied Mathematics，2007，206（2）：1070-1081.

[25]周燕，劉培玉，趙靜，等.基于自適應慣性權重的混沌粒子群算法[J].山東大學學報：理學版，2012（3）：27-32.

[26]Holland J H.Adaptation in natural and artificial systems[M].Cambridge，Massachusetts：MIT Press，1992：87-95.

[27]邢文訓，謝金星.現代優化計算方法[M].北京：清華大學出版社，1999：90-183.

[28]Metropolis N，Rosenbluth A.Rosenbluth metal，equation of state calculations by fast computing machines[J].Journal of Chemical Physics，1953，56（21）：1087-1092.

[29]龔純，王正林.精通MATLAB最優化計算[M].2版.北京：電子工業出版社，2012：273-311.

[30]彭曉波，桂衛華，黃志武，等.GAPSO：一種高效的遺傳粒子混合算法及其應用[J].系統仿真學報，2008，20（18）：5025-5027.