基于蒙特卡洛方法的液壓泵變量伺服機構穩健性優化

汪滸江，毛明，唐守生，冀海

(中國北方車輛研究所 車輛傳動重點實驗室，北京100072)

0 引言

液壓泵變量伺服機構是一個典型的機械液壓位置伺服系統，此類機構廣泛應用于飛機、導彈、仿形機床等領域［1］。當其應用于履帶車輛靜液轉向操縱時，控制系統的跟蹤精度及穩健性非常重要。履帶車輛使用條件惡劣，實際系統工作時存在許多顯著的不確定性因素，如不穩定的伺服控制油壓、不確定的液壓油泄漏量、駕駛員操縱機構中機械零件的變形、磨損、裝配間隙以及轉向負載的動態變化等，因此需要特別關注液壓泵變量伺服機構在面對顯著不確定性因素時，系統的工作性能能否保證穩定，即保證系統性能的穩健性。

針對液壓泵變量伺服機構在動態特性建模分析與仿真、系統參數優化等方面，研究人員均已做過大量的工作［2-6］，而關于如何考慮伺服機構中的不確定性因素，研究系統性能的穩健性及其優化問題，尚未見到相關文獻資料。

穩健性優化設計思想源自日本田口在20 世紀二戰之后提出的產品質量管理思想，其基本思想是，在不消除和不減小不確定性源的前提下，通過對可控因素的合理匹配并控制其容差，降低產品在設計點上的敏感性，控制并減小目標函數的波動，以實現產品質量特性“均值趨于最優”、“均方差趨于最小”的目的［7-8］。

本文利用蒙特卡洛方法建立了適用于液壓泵變量伺服機構的穩健性優化設計新方法。根據履帶車輛對靜液轉向控制機構的特殊需求，以系統性能的穩健性為優化目標，以系統關鍵結構參數名義值為設計變量，利用模擬退火算法實現優化問題的求解，并給出具體的應用實例。

1 工作原理

圖1為液壓泵變量伺服機構的結構示意圖，其由三位四通轉閥、雙作用液壓缸、活塞、反饋撥叉、對中裝置、操縱連桿機構等組成，其中，轉閥用于控制油液的流量和方向，活塞用于驅動斜盤克服負載擺動一定角度，實現柱塞泵排量變化，反饋撥叉用于實現外部反饋。圖2為液壓泵變量伺服機構的工作原理圖。轉閥中，P 為進油口，T 為回油口，A、B 為工作油口，M、G 為柱塞泵進、出油口。初始狀態時，液壓缸中活塞處于中位，轉閥處于中位。當駕駛員操縱車輛轉向時，操縱連桿機構動作，帶動閥芯動作，轉閥隨之開啟。此時若轉向信號使轉閥左位接通，則P 口與A 口接通，B 口與T 口接通，壓力油液進入液壓缸左腔推動活塞向右移動。反饋撥叉實時感知活塞位移并反饋給轉閥閥套，并促使轉閥關閉，活塞隨之停止運動。由此可見，當駕駛員轉向操縱信號(方向盤轉角)為一定值時，轉閥閥芯輸入角度就為一確定量，進入穩定狀態后活塞的位移也將是一確定量。活塞推動斜盤轉動，進而調節柱塞泵的排量，由此實現對履帶車輛轉向半徑的穩定控制。液壓泵變量伺服機構作為履帶車輛轉向的控制機構，其必須具有足夠的穩定性以保證轉向的可控性和平穩性，必須具有足夠的跟蹤精度以保證轉向過程的準確性。在該系統中，閥芯的轉角控制信號θi為系統的輸入，活塞的位移y 為系統的輸出。

圖1 變量伺服機構結構示意圖Fig.1 Structure diagram of stroking mechanism

圖2 變量伺服機構工作原理圖Fig.2 Schematic diagram of stroking mechanism

2 動力學模型

根據工程流體力學相關理論［9］，具有匹配、對稱節流閥口的理想零開口閥的壓力-流量特性方程為

式中:qL為負載流量(m3/s);w 為閥口梯度(轉閥節流口的過流面積對其開口角度的變化率(m2/rad));θ 為轉閥開口角度(rad);ρ 為油液密度(kg/m3);ps為伺服控制油壓(Pa);pL為負載壓降(液壓缸兩腔油液壓力之差，Pa);Cd為流量系數，其是一個常值，轉閥節流口可視為薄壁孔口，根據文獻［10］，其值可取0.62.

液壓缸的流量連續性方程［9］為

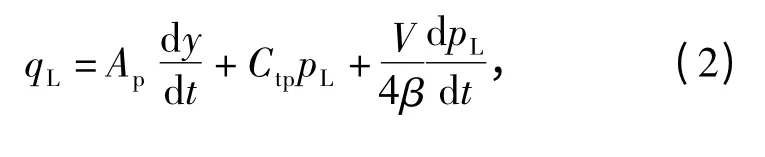
式中:Ap為活塞面積(m2);y 為活塞位移(m);Ctp為液壓缸總泄漏系數(m3/(s·Pa));V 為總壓縮體積(轉閥與液壓缸間油道及液壓缸兩腔的油液總體積，m3);β 為油液有效體積彈性模量，通常，如果沒有β 的實測值，計算時其值可取在700 ～1 200 MPa之間［9］。

(2)式中:等號右邊第1 項為推動活塞運動所需流量;第2 項為總泄漏流量;第3 項為總壓縮流量(由于轉閥與液壓缸間油道及液壓缸兩腔的油液壓縮變形而引起的流量)。

液壓缸和負載的力平衡方程為

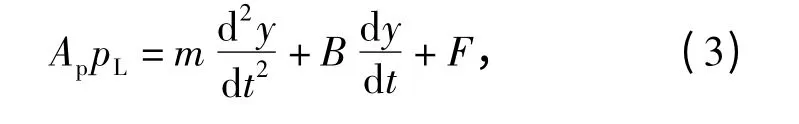
式中:m 為等效負載質量(kg);B 為等效負載阻尼系數(N·s/m);F 為活塞上受到的任意外負載力(N).

反饋撥叉將活塞的位移y 變換成轉閥閥套的轉角θf，如果不考慮結構的變形和間隙誤差，有

式中:θf的單位是rad;a 為反饋撥叉長度(m).

駕駛員操縱方向盤的動作通過操縱連桿機構作用于閥芯，而反饋撥叉作用于閥套，閥芯與閥套的相互關系確定了轉閥閥口的實際開口角度θ.

式中:θi為方向盤轉角信號通過操縱連桿機構作用于閥芯的輸入角度(rad)。

(1)式～(5)式描述了液壓泵變量伺服機構的動態工作特性，其中(1)式考慮了流量與壓力間的非線性關系，(2)式考慮了油液的壓縮和泄漏，(4)式考慮了反饋結構的非線性特性。(1)式～(5)式比較精確地描述了系統輸入θi、輸出y、負載F 間的動態關系。根據(1)式～(5)式利用MATLAB 建立變量伺服機構仿真模型。

3 評價指標

3.1 系統的跟蹤精度

系統的跟蹤精度IAE 定義為誤差絕對值的積分［11］。

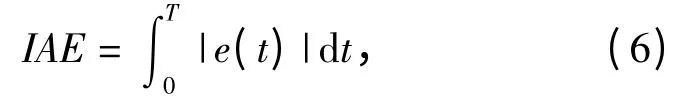
式中:e(t)為系統的誤差，它定義為系統輸出量的期望值與實際值之差，它是一個時間的函數;T 為累計誤差時長。

對于一個控制系統，系統的誤差e(t)主要由系統參數、輸入信號和負載決定［12］。從設計的角度講，最關心通過合理匹配系統參數以減小系統誤差，因此在分析之前，需要定義清楚系統的輸入信號及負載形式。在文獻［3，5］中，相關學者曾將液壓泵變量伺服機構所受外負載力簡化考慮為一個恒值力。此處，用伺服機構克服恒值外負載力，對目標信號θ*=ymaxsin(2πt)的累積跟蹤誤差IAE 來評價系統的跟蹤精度。此時，控制指令信號應為

式中:R=arctan(ymax/a)，ymax為活塞行程的一半。

圖3給出了仿真獲取的某一液壓泵變量伺服機構實際響應與目標信號之間的關系。由圖3可以看出，活塞的位置響應完全跟隨目標信號而變化，其跟蹤誤差可能為正，也可能為負。此跟蹤誤差直接體現在履帶車輛轉向軌跡的可控性上，過大的跟蹤誤差導致的轉向超前與滯后均不利于駕駛員對車輛的操縱。

圖3 變量伺服機構的跟蹤誤差e(t)Fig.3 Target signal and actual response of stroking mechanism

3.2 幅值裕量

穩定性是一個系統可控的先決條件。零位幅值裕量可用于評價液壓泵變量伺服機構相對穩定性的大小，其值為正，則系統穩定，其值越大，則系統相對穩定性越好。幅值裕量Kg計算公式［9］為

式中:ωh為系統的液壓固有頻率;ξh為系統零位下的阻尼比，通常取值0.1 ～0.2;Kv為系統的開環增益。

式中:Kq為轉閥的流量增益;Kf為反饋增益。理想零開口閥零位下的流量增益為

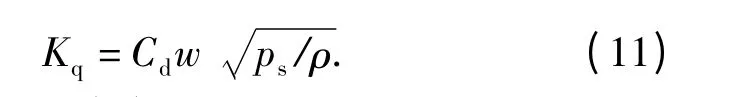
反饋增益Kf由(4)式在y =0 處利用泰勒級數展開，忽略高階無窮小項得到:

根據(8)式～(12)式，推導得液壓泵變量伺服機構零位下的幅值裕量為

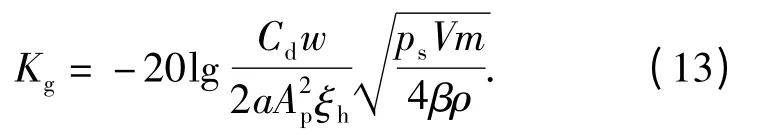
4 蒙特卡洛模型

蒙特卡洛方法是一種以概率統計理論為基礎的計算機隨機模擬方法，二戰末為解決核武器研制過程中遇到的中子擴散問題而首次提出。作為當前比較成熟的一種不確定性分析方法，非常適用于非線性系統的分析［13-14］。

從設計的角度，影響產品質量特性的因素可分為兩類:一類是設計過程中易于控制的參數，如產品的幾何尺寸，稱可控因素;另一類是設計過程中不易控制的參數，如泄漏量、工作環境參數等，稱噪聲因子。變量伺服機構中反饋撥叉長度a、閥口梯度w、活塞直徑D、伺服控制油壓ps、總泄漏系數Ctp直接決定系統的穩定性及跟蹤精度，是系統質量特性的關鍵影響因素。其中，a、w、D 為結構參數，在設計過程中易于通過調整其設計名義尺寸加以控制，為可控因素。伺服控制油壓ps、總泄漏系數Ctp在設計過程中不易保證，為噪聲因子。結構參數由于加工誤差，使用過程中的磨損、變形，具有不確定性。伺服控制油壓、總泄漏系數存在波動，也具有不確定性。這些不確定性可以利用概率密度分布函數來描述。參數的不確定性進一步導致系統性能的波動，現代穩健性設計思想即追求在設計階段通過對可控因素的合理匹配，抑制噪聲因子在使用過程中對產品質量特性的影響，并減小產品質量特性在設計點處的敏感度。

綜合考慮存在不穩定的伺服控制油壓、不確定的泄漏量以及由于加工誤差、磨損、變形等導致結構參數實際值相對名義值的波動，利用圖4所示蒙特卡洛模擬流程圖可獲取某一設計參數組合［a*w*D*］下系統性能指標的均值和標準差。

根據圖4所示流程圖在MATLAB 中建立蒙特卡洛模型。其中，a*、w*、D*分別為反饋撥叉長度、閥口梯度、活塞直徑的設計名義值，是蒙特卡洛模型的輸入;a(i)、w(i)、D(i)、ps(i)、Ctp(i)(i =1，2，…，N)分別為反饋撥叉長度、閥口梯度、活塞直徑、伺服控制油壓、總流量泄漏系數實際值的模擬值，其服從所定義的概率分布，是蒙特卡洛模型的中間狀態量;IAE、Kg的均值、標準差通過對某一設計參數組合下IAE、Kg的響應面統計分析獲取，為蒙特卡洛模型的輸出。

圖4 蒙特卡洛模擬流程圖Fig.4 Flow chat of Monte Carlo simulation

5 穩健性優化

傳統設計中，為了控制產品質量特性的波動，通常采取減小影響因素容差來實現，此以增加制造和使用成本為代價。實際上，對于一個復雜的系統，產品的質量特性與影響因素之間通常存在復雜的非線性特性。穩健性設計正是要合理利用這種非線性關系，力圖將設計點確定在產品質量特性的低敏感區。此種設計方法，在提升產品性能并減小其性能波動的同時，并不增加成本。

此處建立液壓泵變量伺服機構的穩健性優化設計模型，試圖在不苛刻工藝及使用條件的情況下，即結構參數及噪聲因子變動范圍均不變的情況下，通過優化匹配關鍵結構參數的設計名義值，達到以下兩點設計效果:1)提升產品性能，使跟蹤精度、穩定性指標“均值趨于最優”;2)提升變量伺服機構抵抗結構參數、伺服控制油壓以及總油液泄漏量變動的能力，即使跟蹤精度、穩定性指標“均方差趨于最小”。

通過前面的研究可以看出，系統的優化目標是系統的跟蹤精度最優、穩定性最優，并保持系統性能的穩健性最優。因此有IAE 均值最小、Kg均值最大，且IAE、Kg標準差最小。則其目標函數表達式為

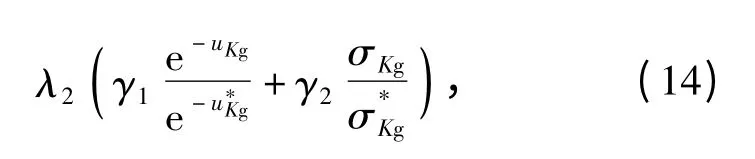
式中:uIAE、σIAE、uKg、σKg分別為某一設計參數組合(a*w*D*)下性能指標IAE、Kg的均值和標準差;λ1、λ2、β1、β2、γ1、γ2為加權系數，分別為優化前系統性能指標IAE、Kg的均值和標準差，其對待優化項進行歸一化處理，以消除優化過程中uIAE、σIAE、uKg、σKg數量級差異對目標函數的影響。

以液壓泵變量伺服機構的關鍵結構參數反饋撥叉長度、閥口梯度、活塞直徑的設計名義值為優化變量，即:

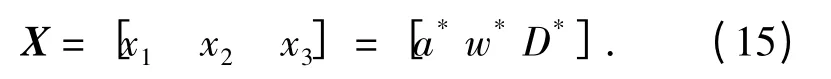
以上關鍵結構參數受總體結構尺寸的限制，即設計變量名義值必須在一定范圍內選擇，即

式中:xli、xhi分別為反饋撥叉長度、閥口梯度、活塞直徑名義值的上、下限。

上述優化模型可選擇模擬退火算法進行求解。

6 實例

6.1 實例參數

某液壓泵變量伺服機構，系統參數如表1所示。

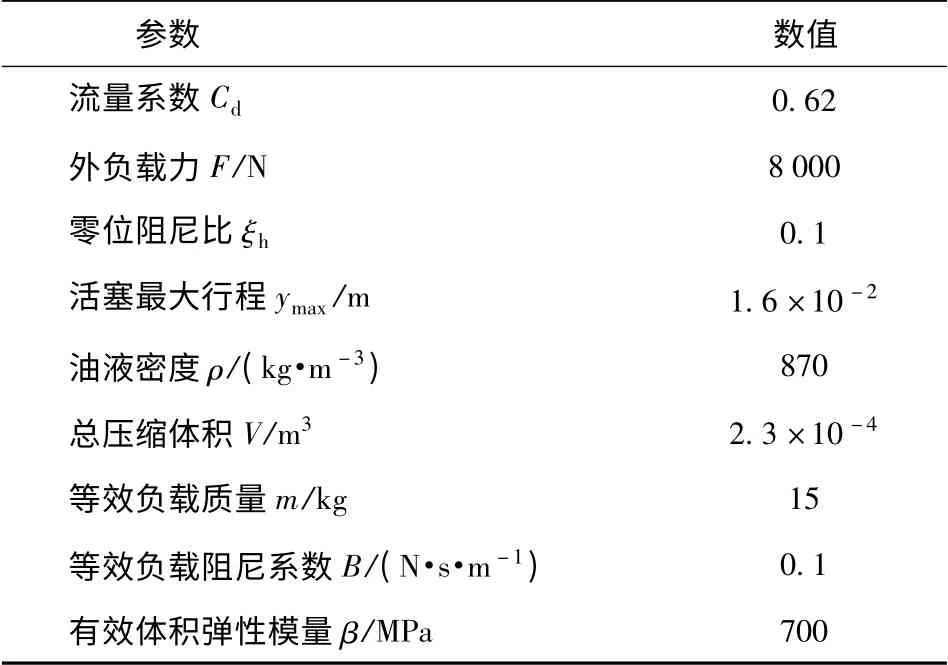
表1 變量伺服機構系統參數Tab.1 System parameters of stroking mechanism

6.2 穩健優化模型參數

反饋撥叉長度、閥口梯度、活塞直徑名義尺寸的上、下限分別為:x1∈［22 mm 51 mm］;x2∈［35 mm2/rad 90 mm2/rad］;x3∈［28 mm 70 mm］.IAE 累計誤差時長取一個正弦周期。視各優化子項同等重要，故各加權系數均取值0.5.

6.3 設計變量及噪聲因子概率分布

該實例中，反饋撥叉長度近似服從a ～N(a*，0.332)，單位mm;閥口梯度近似服從w ～N(w*，3.32)，單位mm2/rad;活塞直徑近似服從D ～N(D*，0.332)，單位mm;總泄漏系數近似服從Ctp～N(8.5 ×10-12，(1.7 ×10-12)2)，單位m3/(s·Pa);伺服控制油壓近似服從ps～N(5，0.52)，單位MPa.以上所用各參數概率分布，是作者基于經驗而做出的基本假設，有其局限性，更準確的概率分布依賴于進一步的試驗研究及數據統計，但并不影響本文述及的理論和方法。

6.4 優化結果

蒙特卡洛模擬次數取100，選擇模擬退火算法完成優化，優化前后結果對比如表2所示。

表2 穩健性優化前后關鍵結構參數對比Tab.2 Key structure parameters before and after optimization

6.5 穩健性分析

分別對優化前、后結果應用蒙特卡洛模擬進行穩健性分析，蒙特卡洛隨機采樣次數N 取5 000，優化前、后各性能指標對比如表3所示。

表3 穩健性優化前后各性能指標對比Tab.3 Performance indexes before and after optimization

直方圖組數取100，優化前、后IAE、Kg響應面模型概率分布直方圖如圖5～圖8所示。

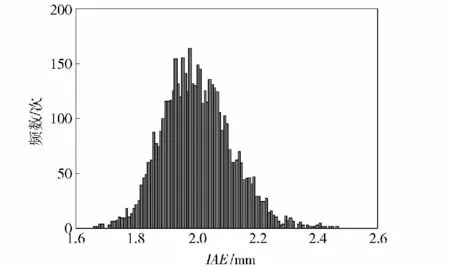
圖5 優化前IAE 響應面概率分布Fig.5 Response surface of IAE before optimization

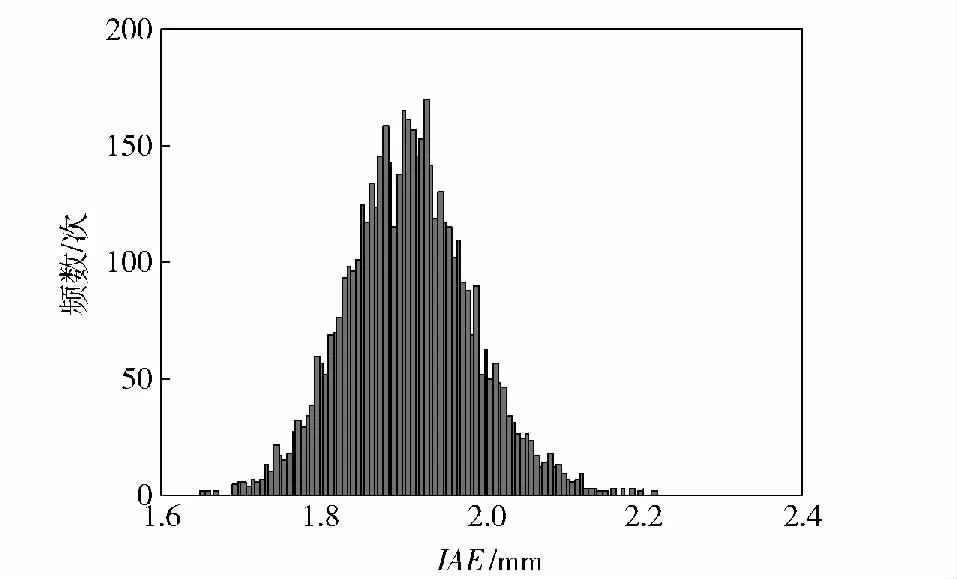
圖6 優化后IAE 響應面概率分布Fig.6 Response surface of IAE after optimization

圖7 優化前Kg響應面概率分布Fig.7 Response surface of Kg before optimization

圖8 優化后Kg響應面概率分布Fig.8 Response surface of Kg after optimization

對仿真結果進行正態分布擬合，圖9、圖10 分別為IAE、Kg優化前后的概率密度分布函數對比圖。

從圖5～圖10 可以看出，經過穩健性優化，變量伺服機構跟蹤精度IAE“均值趨于最小，均方差趨于最小”，零位幅值裕量Kg“均值趨于最大，均方差趨于最大”，表明經過穩健性優化，不僅保證系統具備良好的跟蹤精度及相對穩定性，而且顯著提升了系統抵抗結構參數、油液參數變動的能力，系統在惡劣環境下穩定工作的能力顯著增強，穩健性優化效果顯著。

圖9 優化前后IAE 概率密度分布函數Fig.9 Probability density functions of IAE before and after optimization

圖10 優化前后Kg概率密度分布函數Fig.10 Probability density functions of Kg before and after optimization

7 結論

本文針對履帶車輛對靜液轉向操縱機構性能及穩健性的特殊需求，提出了變量伺服機構穩健性設計新方法。以系統動態跟蹤精度、相對穩定性性能指標分布的均值及標準差為優化目標，以反饋撥叉長度、閥口梯度、活塞直徑的設計名義值為優化變量，利用蒙特卡洛方法構建液壓泵變量伺服機構的穩健性優化設計模型，利用模擬退火算法實現優化問題的求解。

通過應用案例可以看出，穩健性優化效果顯著。在相同結構參數及噪聲因子波動水平下，通過優化匹配反饋撥叉長度、閥口梯度、活塞直徑的設計名義值，系統的跟蹤精度及相對穩定性大幅提升，穩健性大幅提升。表明所提出的穩健性優化設計新方法在不增加制造工藝，不減小環境干擾的情況下，通過選取關鍵參數并進行優化匹配設計，不僅能提升變量伺服機構各項性能，而且顯著增強了系統抵抗結構參數、油液參數變動的能力，此設計方法對獲得“低成本、高性能、高惡劣環境耐受度”的裝備具有參考意義。

References)

［1］張利平. 液壓控制系統及設計［M］. 北京:化學工業出版社，2007.ZHANG Li-ping. Control and design of hydraulic control system［M］.Beijing:Chemical Industry Press，2007. (in Chinese)

［2］郭杰，劉廣瑞.軸向柱塞泵變量機構的數學建模及控制系統仿真分析［J］.機床與液壓，2013，41(3):106 -109.GUO Jie，LIU Guang-rui. Mathematical modeling of the stroking mechanism of axial piston pump and its control system simulation analysis［J］. Machine Tool &Hydraulics，2013，41(3):106 -109. (in Chinese)

［3］焦宗夏，王占林. 變量機構主要參數的優化設計［J］. 機床與液壓，1993，21(6):339 -342.JIAO Zong-xia，WANG Zhan-lin. The optimization of the stroking mechanism main parameters ［J］. Machine Tool &Hydraulics，1993，21(6):339 -342. (in Chinese)

［4］宋俊. 軸向柱塞泵變量機構功率匹配優化設計［J］. 機械設計與制造，2000(3):50 -51.SONG Jun. The optimization of axial piston pump stroking mechanism by matching power［J］. Machinery Design ＆ Manufacture，2000(3):50 -51. (in Chinese)

［5］李澤松，寇子明. A4VG 系列變量泵伺服機構動態特性分析［J］.煤礦機電，2005(2):8 -9，12.LI Ze-song，KOU Zi-ming. Servo dynamics analysis of A4VG series variable displacement pumps［J］. Colliery Mechanical ＆ Electrical Technology，2005(2):8 -9，12. (in Chinese)

［6］李磊，許明恒，于蘭英，等. 位移-力反饋型變量機構理論建模與試驗研究［J］.機械科學與技術，2012，31(4):578 -582.LI Lei，XU Ming-heng，YU Lan-ying，et al. Theoretical modeling and experimental research on variable-displacement mechanism with displacement-force-feedback［J］. Mechanical Science and Technology for Aerospace Engineering，2012，31(4):578 -582.(in Chinese)

［7］鄭健，成艾國，董立強，等.田口魯棒設計方法在汽車耐撞性優化中的應用［J］.汽車工程，2011，33(9):772 -776.ZHENG Jian，CHENG Ai-guo，DONG Li-qiang，et al. The application of Taguchi robust design to vehicle crashworthiness optimization［J］. Automotive Engineering，2011，33(9):772 -776. (in Chinese)

［8］李玉強，崔振山，阮雪榆，等. 6σ 概率優化設計方法及其應用［J］.中國機械工程，2004，15(21):1916 -1919.LI Yu-qiang，CUI Zhen-shan，RUAN Xue-yu，et al. 6σ based probabilistic design optimization method and applications［J］. China Mechanical Engineering，2004，15(21):1916 -1919. (in Chinese)

［9］王春行. 液壓控制系統［M］. 北京:機械工業出版社，1995.WANG Chun-xing. Hydraulic control system［M］. Beijing:China Mechine Press，1995. (in Chinese)

［10］張也影. 流體力學［M］. 北京:高等教育出版社，1999.ZHANG Ye-ying. Fluid mechanics［M］. Beijing:Higher Education Press，1999. (in Chinese)

［11］Richard C D，Robert H B. 現代控制系統［M］. 謝紅衛，鄒蓬興，張明，等，譯. 北京:高等教育出版社，2001.Richard C D，Robert H B. Modern control system［M］. XIE Hong-wei，ZOU Peng-xing，ZHANG-Ming，et al，translated.Beijing:Higher Education Press，2001. (in Chinese)

［12］陳康寧. 機械工程控制基礎［M］. 西安:西安交通大學出版社，1997.CHEN Kang-ning. The control basis of mechanical engineering［M］.Xi’an:Xi’an Jiaotong University Press，1997. (in Chinese)

［13］朱輝，劉義保，游運，等. 蒙特卡羅方法與擬蒙特卡羅方法的歷史、現狀及展望［J］. 東華理工大學學報:自然科學版，2010，33(4):357 -362.ZHU Hui，LIU Yi-bao，YOU Yun，et al. Monte Carlo method and quasi-Monte Carlo method［J］. Journal of East China Institute of Technology:Natural Science，2010，33(4):357 -362.(in Chinese)

［14］張超，陳磊，陳宗基，等. 基于視覺的UCAV 自主著陸蒙特卡洛仿真研究［J］.系統仿真學報，2010，22(9):2235 -2240.ZHANG Chao，CHEN Lei，CHEN Zong-ji，et al. Monte Corlo simulation for vision-based autonomous landing of unmanned combat aerial vehicles ［J］. Journal of System Simulation，2010，22(9):2235 -2240. (in Chinese)