某雙幅雙塔四索面矮塔斜拉橋混凝土箱梁局部早期收縮裂縫分析

吳 慶，徐文蘇，李 光

(江蘇科技大學土木工程與建筑學院，江蘇鎮江212003)

大體積混凝土在施工過程中的裂縫控制一直是困擾工程技術人員的一大難題，其中一項重要原因就在于混凝土自身水化熱效應難以避免［1］.如果采用分層澆筑的方式，各澆筑層結合面處由于混凝土齡期不同，后澆筑混凝土的收縮變形受到先澆混凝土的約束而產生拉應力［2］.一旦該拉應力超過混凝土對應齡期的抗拉強度，就會出現裂縫災害，影響結構安全.

混凝土箱梁0號塊體積較大，在分層澆筑過程中如果不對混凝土收縮效應加以考慮，極易導致分層結合面出現裂縫［3］.影響混凝土收縮變形的因素有很多，如構件尺寸、外界環境和材料自身特性等.文中以鹽城某矮塔斜拉橋施工過程中0號塊頂板出現裂縫為工程背景，從施工控制的角度，對箱梁早期裂縫進行了分析研究，為今后國內外相關工程的施工提供理論參考.

1 工程背景及分析模型

鹽城某雙幅雙塔四索面矮塔斜拉橋，主梁半幅采用單箱三室小懸臂斜腹板斷面.其中0號塊箱梁長12.0 m，橋面寬度為24.25 m，中支點6 m范圍內梁高8.0 m，向外至0號塊斷面梁高線性變化為7.77 m，同時頂板、底板和腹板厚度均有不同程度變小.0號塊端點斷面圖如圖1.

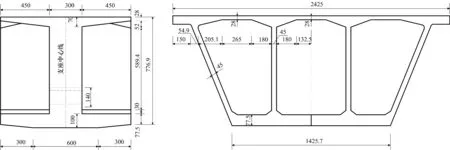
圖1 0號塊斷面(單位:cm)Fig.1 Section of block 0(unit:cm)

右幅9#墩上0號塊梁段在澆筑后不久出現裂縫，裂縫主要發生在箱室上方的頂板靠近腹板和橫隔板處(圖2).從現場觀測結果總結出，雖然裂縫分布較廣，主要較大裂縫出現在腹板和橫隔板處，且開展方向與腹板和橫隔板方向相同.查找施工記錄，發現該0號塊第一次混凝土澆筑時間為2013年8月1日，當天澆筑完成.第二次澆筑時間原計劃在8月12日，但由于天氣等其他原因，推遲到8月29日才完成.

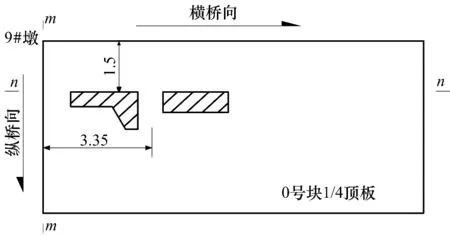
圖2 頂板裂縫位置(單位:m)Fig.2 Position of roof cracks(unit:m)

研究選取整個0號塊為對象進行箱梁0號塊的收縮特性分析.利用大型有限元分析軟件ANSYS建立0號塊裂縫有限元模型，暫不考慮普通鋼筋對混凝土收縮的約束作用.根據0號塊的對稱性，選取箱梁1/4作為研究對象.C55鋼筋混凝土采用SOLID65單元模擬，彈性模量為3.55×104MPa，線膨脹系數為1×10-5，不考慮重力效應.混凝土邊界條件采用對稱截面施加對稱約束，收縮效應利用等效溫降的方法進行模擬［4］.0號塊空間有限元模型如圖3.

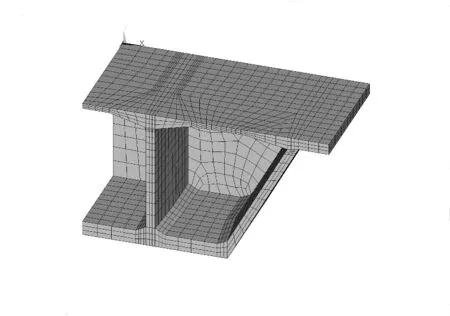
圖3 0號塊有限元模型Fig.3 Finite element model of block 0

2 箱梁0號塊混凝土收縮效應分析

在箱梁0號塊收縮效應分析中，考慮混凝土分層澆筑間隔時間為28 d，計算齡期至3個月后兩澆筑層收縮差異最大時期應力分布［5］.第一次混凝土澆筑到距離箱梁頂面1m處，其余為后澆層，根據等效溫降原理對后澆層收縮當量溫差-15℃處理［6-7］.本次模擬僅考慮后澆混凝土的收縮作用，對于結構自重、預應力和混凝土徐變效應均不予考慮.

2.1 0號塊整體收縮效應分析

有限元計算結果表明，箱梁0號塊單獨在收縮效應作用下，大部分主體應力在0.92 MPa以下，主要拉應力區域集中在頂板上，拉應力較大區域與實測頂板裂縫位置大致吻合.從圖4中可以看出，頂板與橫隔板板交界處的主拉應力遠大于其他部位，腹板斷面兩澆筑層結合面處產生很大應力集中.說明后澆層在自身收縮變形過程中受到先澆層的約束作用，拉應力主要集中在頂板與腹板交接面.同時，可以看出除個別倒角之外，在頂板厚度變化區域主應力最大，應力值在1.49～2.06 MPa范圍內.

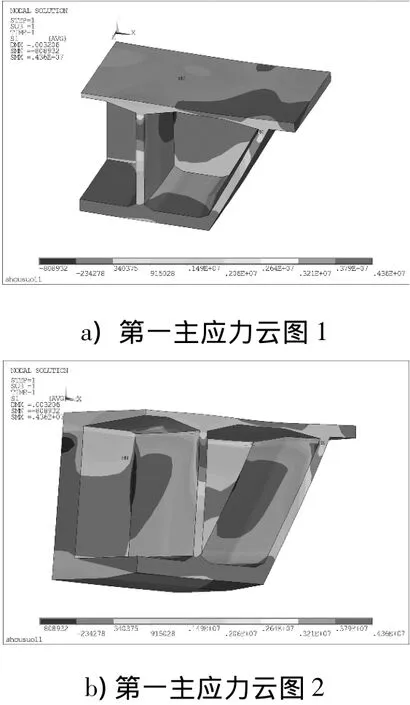
圖4 0號塊主應力云圖Fig.4 Principal stress nephogram of block 0

2.2 頂板收縮應力分析

選取圖2中豎向m-m截面和n-n截面作為研究路徑，其中m-m截面為沿順橋向中心線的豎向截面，n-n截面為橫隔板端處橫橋向斷面.在斷面與頂板頂面交線上取若干點的主拉應力作圖，如圖5(圖中LH為距橫橋向中心線的距離，LS為順橋向中心線的距離).

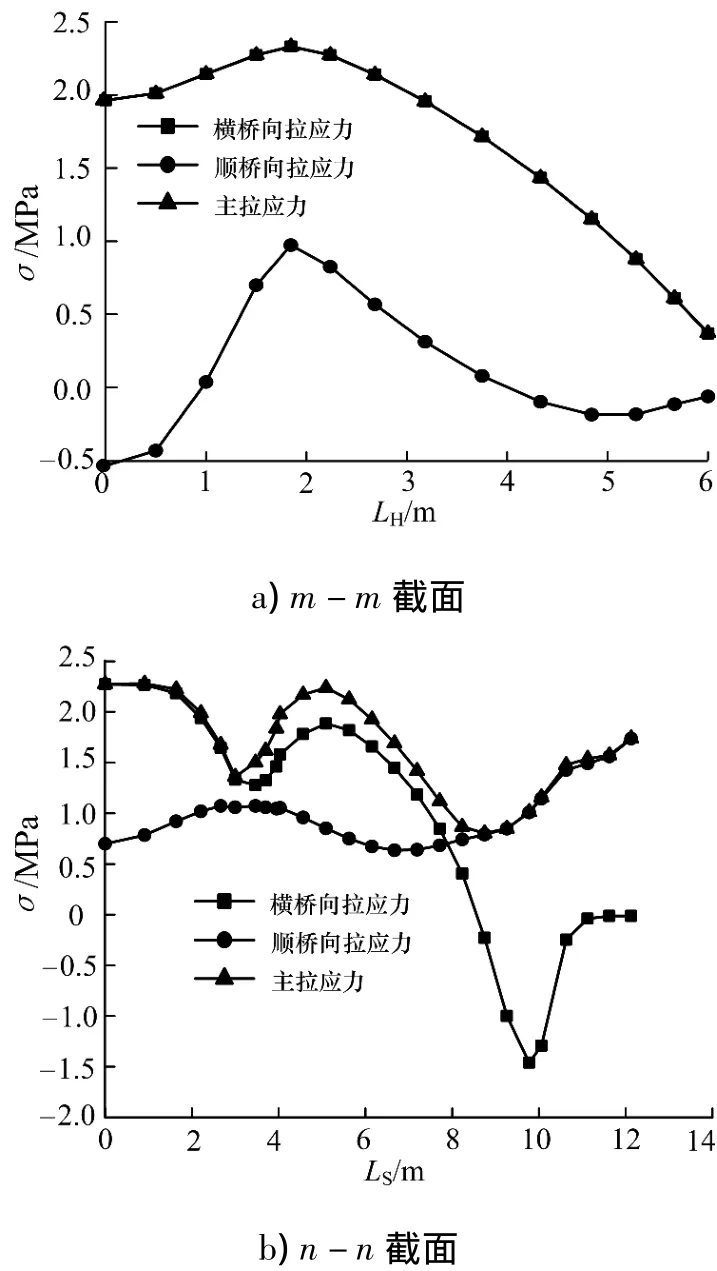
圖5 截面應力分布圖Fig.5 Stress distribution of sections

通過圖5兩截面應力分布可知，截面測點主拉應力總體偏大，最大應力約為2.3 MPa.對于m-m截面，橫橋向應力與主應力接近重合，說明最大主應力方向與縱向一致;對于n-n截面，在0～2.5m范圍內主應力與橫橋向方向一致，2.5～8 m范圍內仍由橫橋向拉應力為主應力做主要貢獻，8 m范圍以外主應力方向轉變為順橋方向.此現象表明橫隔板和腹板對頂板收縮應力的分布有很大影響.

3 箱梁0號塊混凝土收縮裂縫參數研究

前述內容以某橋箱梁0號塊頂板為例，分析了后澆層收縮效應下頂板應力的分布規律以及影響應力分布的因素.在箱梁0號塊收縮裂縫參數研究中，分別對m-m截面和n-n截面在不同分層澆筑齡期、不同后澆層厚度和不同線膨脹系數下收縮應力的變化規律進行研究.

3.1 分層澆筑齡期間隔的影響

在進行不同分層澆筑齡期對混凝土收縮裂縫影響的研究中，分別考慮前后澆筑層齡期間隔取為7，14，21，28 d，對應混凝土收縮當量溫差分別為-8.1，-11.5，-13.8，-15℃.

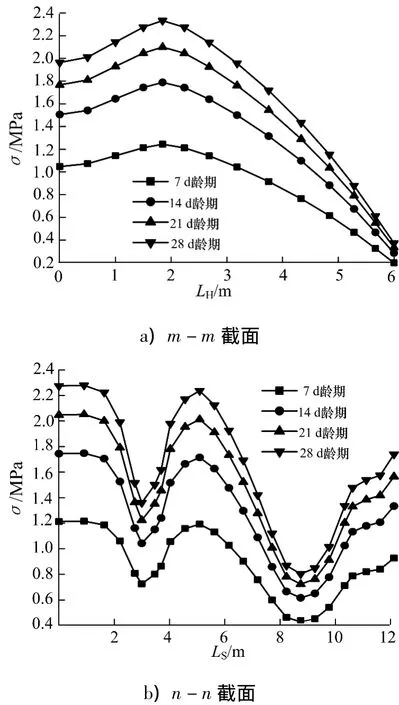
圖6 不同齡期截面應力對比Fig.6 Comparison of different ages for section stress

從圖6中可以看出，分層澆筑齡期的大小對頂板應力值影響很大而對頂板的應力分布影響并不明顯.每增加7d的齡期間隔，箱梁頂板的主應力值分別增加43.8%，17.4%和11.1%，這符合混凝土隨齡期增長收縮逐漸減緩的規律［8-9］.

以上分析說明，澆筑混凝土箱梁時，盡量減少分層澆筑間隔時間有利于控制收縮裂縫的發生，越早施工后澆層，混凝土的收縮效應越小，越利于箱梁的裂縫控制.

3.2 不同后澆層厚度的影響

在進行后澆層厚度對混凝土收縮裂縫影響的研究中，分別考慮后澆層澆筑高度取為1.0，1.5，2，2.5 m，計算齡期取后澆層3個月后的的應力分布(圖7).

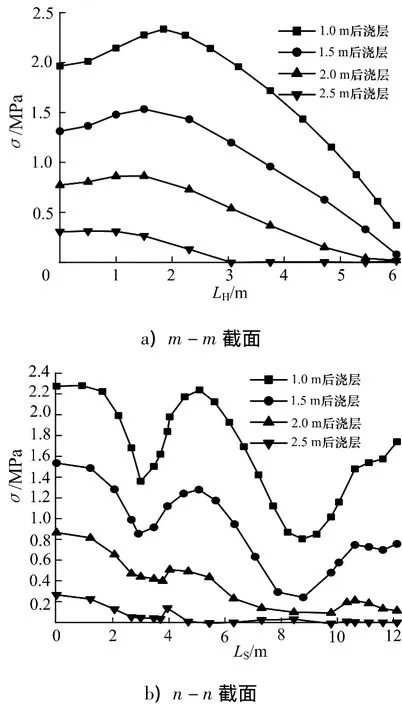
圖7 不同后澆層厚度截面應力對比Fig.7 Comparison of different last layer thicknesses for section stress

從圖7中可以看出，后澆層厚度對頂板應力的大小和分布均有很大影響.施工縫每下移0.5 m，頂板主應力值相應減小0.6 MPa左右，且減小值變化不大.隨著后澆層厚度的增加，應力值顯著下降，應力曲線逐漸趨于平滑也表明箱梁橫隔板和腹板對收縮應變的約束作用越來越小.

以上分析表明，在箱梁施工階段充分考慮降低施工縫可以有效地降低頂板拉應力，但降低施工縫對鋼筋綁扎及混凝土振搗要求較高，必須同時考慮施工工藝的可行性與操作簡便性，選擇最科學和經濟的施工方案.

3.3 不同線膨脹系數的影響

在進行不同線膨脹系數對混凝土收縮裂縫影響的研究中，分別考慮線膨脹系數取為1×10-5，1.1 ×10-5，1.2 ×10-5和1.3 ×10-5，計算齡期取后澆層3個月后的應力分布(圖8).

圖8 不同線膨脹系數截面應力對比Fig.8 Comparison of different linear expansion factors for section stress

從圖8中可以看出，混凝土線膨脹系數每增大10%，應力值相應增加10%，混凝土頂板的主拉應力與線膨脹系數基本呈線性關系，應力分布規律沒有明顯變化.由此可見，箱梁的收縮應力對混凝土材料的線膨脹系數是比較敏感的.

在實際工程施工中，決定混凝土材料線膨脹系數的主要因素是外加劑的添加［10］.因此，在使用外加劑提高快硬混凝土性能的同時，必須把對材料線膨脹系數的影響考慮在內.

4 結論

文中以實際工程為背景，以箱梁0號塊為研究模型，對頂板的收縮效應以及影響頂板收縮裂縫的因素參數進行了分析，得出以下主要結論:

1)箱梁0號塊后澆層收縮效應對整體應力影響不大，但會導致頂板應力集中，誘發早期裂縫的產生.

2)減小分層澆筑齡期可以降低收縮應力，齡期越短，效應減小越明顯;后澆層厚度對頂板收縮應力有決定性作用，收縮接觸面的下移可大大降低頂板收縮應力;收縮應力與混凝土材料線膨脹系數大致呈線性關系.

3)箱梁頂板的早期收縮裂縫是可以通過控制施工參數減小收縮應力來進行預防的.

References)

［1］ 杜海鑫，石雪飛，楊戈平，等.現澆混凝土連續箱梁早期裂縫研究［J］.結構工程師，2013，29(5):161-165.Du Haixin，Shi Xuefei，Yang Geping，et al.Analysis of early age cracks on a cast-in-place concrete continuous box girder［J］.Structural Engineers，2013，29(5):161-165.(in Chinese)

［2］ 蘇祥亞，石雪飛，李森.斜拉橋橋塔不同齡期混凝土結合面收縮效應分析［J］.結構工程師，2012，28(6):166-170.Su Xiangya，Shi Xuefei，Li Sen.Analysis on shrinkage effects of concrete in a cable stayed bridge tower［J］.Structural Engineers，2012，28(6):166 - 170.(in Chinese)

［3］ 尹立威.福建NJG大橋0#塊箱梁裂縫分析［J］.湖南交通科技，2007，33(3):92 -94.

［4］ 王新敏.ANSYS工程結構數值分析［M］.北京:人民交通出版社，2010.

［5］ 石雪飛，馮電視，阮欣，等.大跨徑連續剛構橋不同齡期混凝土結合面收縮影響研究［J］.結構工程師，2009，24(6):76 -79.Shi Xuefei，Feng Dianshi，Ruan Xin，et al.Analysis on shrinkage effects of concrete interfaces in long-span continuous rigid frame bridges［J］.Structural Engineers，2009，24(6):76 -79.(in Chinese)

［6］ 劉偉，董必欽，李偉文，等.大體積混凝土的溫度應力分析及溫度裂縫研究［J］.工業建筑，2008，38(7):79-81.Liu Wei，Dong Bixin，Li Weiwen，et al.The study on thermal stress and temperature crack of underground mass concrete［J］.Industrial Construction，2008，38(7):79-81.(in Chinese)

［7］ 孟江，趙寶俊，劉建梅.混凝土收縮徐變效應預測模型及影響因素［J］.長安大學學報:自然科學版，2013，33(2):56 -62.Meng Jiang，Zhao Baojun，Liu Jianmei. Prediction model an influencing factors for concrete shrinkage and creep effects［J］.Journal of Chang′an University:Natural Science Edition，2013，33(2):56 - 62.(in Chinese)

［8］ 王鐵夢.工程結構裂縫控制［M］.北京:中國建筑工業出版社，2010.

［9］ 中華人民共和國交通部.JTG D62-2004公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.北京:人民交通出版社，2004.

［10］ 呂艷梅，劉立新，徐有鄰.商品混凝土收縮應力實驗研究［J］.東南大學學報:自然科學版，2005，35(Z):144-148.Lü Yanmei，Liu Lixin，Xu Youlin.Experimental study on shrinkage stress of commercial concrete［J］.Journal of Southeast University:Natural Science Edition，2005，35(Z):144-148.(in Chinese)