湍流模型對過冷沸騰計算影響分析

張 蕊，田文喜，叢騰龍，蘇光輝，秋穗正（1．西安交通大學動力工程與多相流國家重點實驗室，陜西西安 710049；2．西安交通大學核科學與技術學院，陜西西安 710049）

湍流模型對過冷沸騰計算影響分析

張 蕊1，2，田文喜1，2，叢騰龍1，2，蘇光輝1，2，秋穗正1，2
（1．西安交通大學動力工程與多相流國家重點實驗室，陜西西安 710049；2．西安交通大學核科學與技術學院，陜西西安 710049）

摘要：采用ANSYS FLUENT14．5分析湍流模型對過冷沸騰的影響，建立多套網格，每套網格采用不同的湍流模型、壁面函數及兩相湍流處理方法，將計算結果與基準實驗數據進行對比，分析網格、湍流模型、壁面函數及兩相湍流處理方法對計算精度的影響。通過分析發現：kε－模型的計算精度高于k－ω模型的；Dispersed方法和Per Phase方法的計算精度相對于Mixture的無明顯提升；增強壁面函數對Y＋≈1的網格無法獲得滿意的計算結果。

關鍵詞：過冷沸騰；湍流模型；計算精度

壓水堆堆芯及蒸汽發生器內均存在過冷沸騰，過冷沸騰可極大地提高換熱表面的換熱系數，但由于傳熱表面熱流密度較高，很容易發生傳熱惡化，當過冷沸騰熱發生偏離核態沸騰（DNB）現象時，由于加熱表面被氣膜覆蓋，加熱表面溫度瞬間飛升并發生燒毀。因此，準確預測臨界熱流密度（CHF）、壁面DNB的發生對于燃料棒的完整性具有重要意義。

過冷沸騰和CHF研究通常基于實驗進行，通過實驗獲得過冷沸騰換熱系數和CHF數據、擬合關系式，為同工況下的設計分析提供參考。由于經驗關系式存在誤差，基于經驗關系式的設計分析均需留有足夠的裕量以保證設備的安全，且經驗關系式僅適用于特定的實驗區間及幾何；另外，對于大型復雜工況，如燃料組件內的過冷沸騰現象，實驗極其昂貴且難以測量。隨著CFD技術的進步及對過冷沸騰機理的認識，研究者提出不同的計算過冷沸騰的CFD模型［1－2］，并對一些簡單幾何內的過冷沸騰現象進行數值模擬。Krepper等［3］對單管內的過冷沸騰進行計算，并嘗試將PRI（Rensselaer Polytechnic Institute）過冷沸騰模型用于燃料組件的過冷沸騰分析；Yan等［4］對燃料組件內的過冷沸騰現象進行模擬，并得到DNB現象。以上分析將RPI過冷沸騰模型用于實際問題的計算，但這些文獻中均未給出湍流模型的選取依據，本文基于RPI過冷沸騰模型和Bartolemei等［5－6］的實驗數據，對過冷沸騰計算中的湍流模型進行敏感性分析。

1 數學物理模型

過冷沸騰的數值分析基于歐拉兩流體模型進行，對氣相和液相分別求解質量、動量、能量守恒方程，同時求解相間質量、動量、能量傳遞模型。

1．1 歐拉兩流體模型

質量守恒方程：

動量守恒方程：

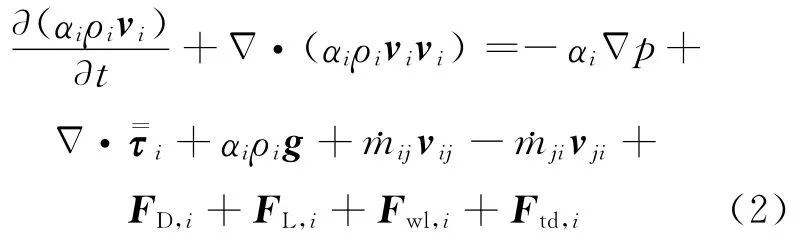
能量守恒方程：

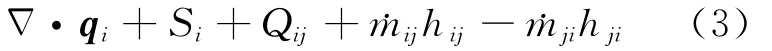
其中：αi、ρi、vi、Si、p、τ＝i、g、vij、Fi、hi、qi和hij分別為i相的體積份額、密度、速度、源項、壓力、應力張量、重力加速度、速度差、相間力、比焓、熱流量和焓差；ij和Qij分別為i相至j相的質量和能量傳遞。應力張量表達式為：

其中：μi和λi分別為i相的剪切黏度和體積黏度；T表示湍流；I＝為單位對角矩陣。

1．2 相間動量傳遞模型

氣液相間作用力包括相間拽力、升力、壁面潤滑力、湍流耗散力，拽力FD為單位體積內氣泡施加在液相上的力：

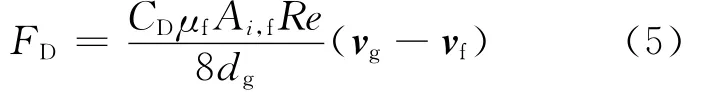
其中：CD為升力系數，由Ishii關系式［7］計算；μf為液相黏度；dg為氣泡直徑；vg和vf分別為氣、液相速度；Ai，f為相界面密度，即：

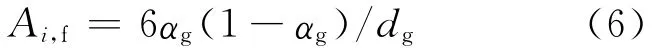
Re為相間相對雷諾數：

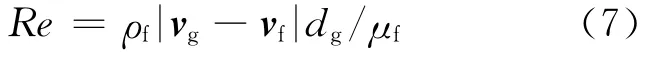
其中：αg為氣相體積份額；ρf為液相密度。

相間升力為由于液相速度梯度而施加在氣相上的力：

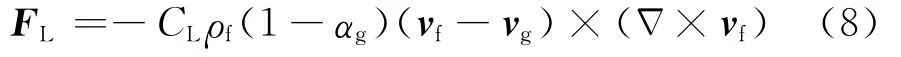
其中，CL為升力系數，由Moraga關系式［8］計算。

壁面潤滑力作用在氣泡上，推動氣泡向主流方向運動，由下式計算：

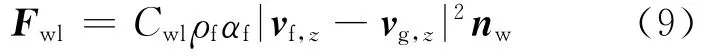
其中：Cwl為壁面潤滑系數，由Antal模型計算［9］；nw為壁面法向矢量。

湍流耗散力用來描述兩相間的湍流相互作用，由下式計算：

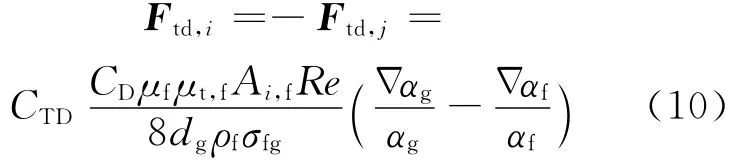
其中：CTD＝1；σfg＝0．9；μt，f為動力黏性系數。

1．3 相間能量傳遞

氣相脫離壁面之后，進入過冷流體時向液體釋熱，單位體積內的傳熱量為：

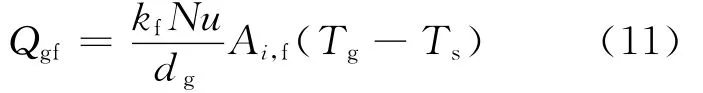
其中：Nu采用Ranz－Marshall公式［10］計算；kf為液相的導熱系數；Tg為氣相溫度；Ts為飽和溫度。

1．4 相間質量傳遞－RPI過冷沸騰模型

采用RPI壁面沸騰模型計算壁面上的沸騰現象及氣泡的冷凝等傳質過程。RPI模型包括壁面熱流密度分配模型和輔助模型。

1）壁面熱流密度分配模型

RPI模型將壁面傳遞給液體的熱流密度分為3部分，即單相液體對流帶走的熱流密度qc、淬滅熱流密度qq和蒸發熱流密度qe。

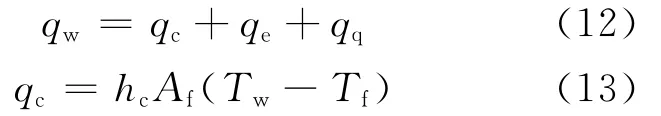
其中：hc為單相對流換熱系數；Af為壁面上液相潤濕面積；Tw為壁面溫度；Tf為液相溫度。壁面液相蒸發產生氣泡時帶走的qe可表示為：

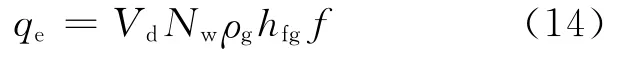
其中：Vd為基于氣泡脫離直徑的氣泡體積；Nw為氣泡核化密度；hfg為汽化潛熱；f為氣泡脫離頻率。qq為氣泡從加熱壁面脫離、液相重新覆蓋壁面時所帶走的熱流密度，表示為：

2）輔助模型

RPI模型的輔助模型包括液相潤濕面積Af、氣泡脫離頻率模型f、氣泡核化密度Nw、氣泡脫離直徑Dw等模型，計算關系式分別為：

其中，Ja為過冷度的Jacob數。

1．5 湍流模型

本文研究目的為分析不同湍流模型對過冷沸騰計算的適用性，在本研究中，分別采用不同的網格數量、不同的湍流模型對基準實驗進行計算，根據網格Y＋不同，所采用的湍流模型包括標準k－ε模型、RNGk－ε模型、可實現k－ε模型、標準k－ω模型、SST k－ω模型。對于k－ε模型，其近壁面網格需滿足Y＋在對數率層，即Y＋＞11．225。根據ANSYS FLUENT手冊，增強壁面函數可對Y＋＜11．225的工況進行計算，并獲得合理的計算結果。考慮到隨著流體被加熱相變，流體流速逐漸增大，對于相同的壁面網格尺度，Y＋也逐漸增大，因此，采用壁面網格Y＋適應性很強的增強壁面函數。在計算中，還進行了近壁面函數的敏感性分析。另外，對于湍流的計算，可采用Mixture、Dispersed 和Per Phase方法。采用Mixture方法時，求解器將氣液相視作混合物，求解1套相應的湍流方程；采用Dispersed方法時，求解器將氣相視作離散相，采用上述指定的湍流模型求解液相湍流參數，采用Tchen理論關系式計算離散相湍流參數，同時考慮相間湍流相互作用；采用Per Phase方法時，對每一相分別求解湍流方程，同時考慮相間湍流相互作用。

不同湍流模型對網格的要求不同，k－ε模型［11－13］要求近壁面網格中心節點位于黏性支層外，需采用壁面函數對近壁面區處理，標準壁面函數、非平衡壁面函數要求壁面網格Y＋大于黏性支層的Y＋（約11．225）；ANSYS FLUENT14．5中引入增強壁面函數，使k－ε模型對Y＋無要求，原則上Y＋越小計算結果越精確［14］。k－ω模型［15－17］要求近壁面網格Y＋≈1，對黏性支層進行詳細的網格劃分；ANSYS FLUENT14．5中引入增強壁面函數，使k－ω模型對Y＋的要求降低，對于Y＋≈10～100的網格，也可計算并得到合理的結果［14］。

本文共采用4套網格，采用不同湍流模型進行計算，湍流模型計算矩陣列于表1。其中StdWF、EnhWF、NeqWF和ScaWF分別表示標準壁面函數、增強壁面函數、非平衡壁面函數和擴展壁面函數，M、D和P分別表示湍流采用Mixture、Dispersed和Per Phase方法計算。

2 實驗工況及計算建模

Bartolemei等［5－6］于1967年和1982年分別對不同直徑的豎直圓管內向上流動的過冷沸騰進行研究，實驗獲得不同壓力、熱流密度、質量流密度、進口過冷度下的空泡份額沿軸向分布以及壁面溫度沿軸向分布。實驗工況列于表2。Bartolemei共給出20余個工況的實驗數據，但其中僅有1個工況（d＝15．4mm，G＝900kg／（m2·s），q＝0．57MW，p＝4．5MPa）給出了沿軸向的內壁面溫度分布及截面平均空泡份額分布，可用于模型的驗證。

考慮到試驗段的對稱性，選取1／4區域作為計算流體域，建模不考慮固體域，幾何模型及網格劃分如圖1所示。

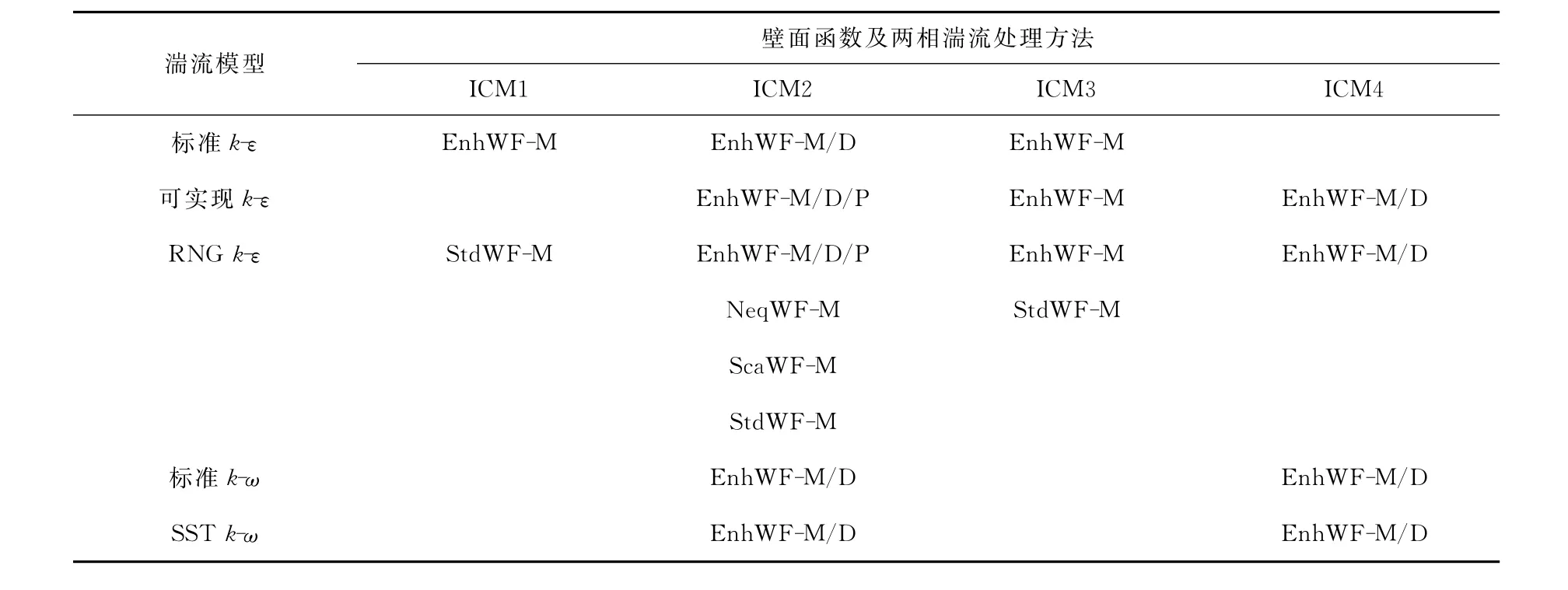
表1 湍流模型計算矩陣Table 1 Computing matrix of turbulence model

表2 Bartolemei實驗參數范圍Table 2 Parameter range of Bartolemei’s experiment

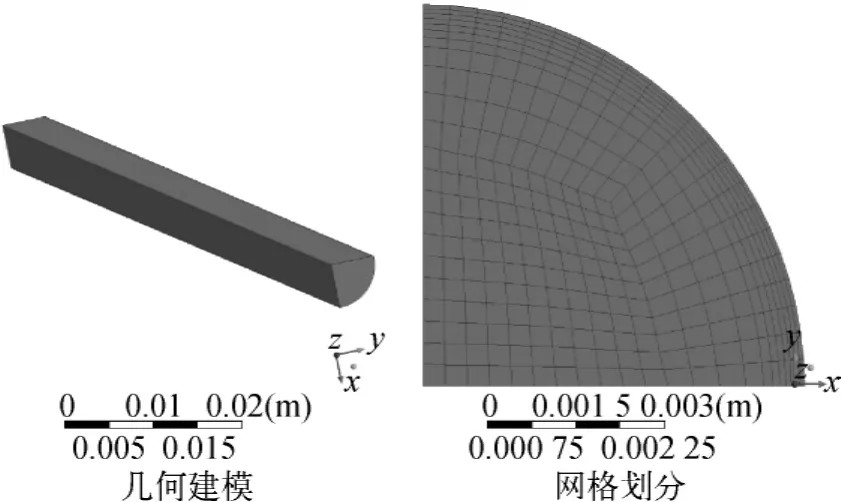
圖1 幾何建模及網格劃分Fig．1 Geometry and grid of calculation domain

3 結果分析

考慮到不同湍流模型及近壁面函數對網格要求不同，本文采用4套網格進行計算，網格數量、近壁面網格幾何尺寸、計算得到的湍流Y＋范圍列于表3。由表3可看出，ICM1和ICM2的網格滿足傳統k－ε模型的近壁面網格要求；ICM4滿足傳統k－ω模型的網格要求；ICM3部分區域近壁面網格中點位于黏性支層以內、部分位于黏性支層之外，屬于傳統湍流模型和壁面函數難以處理的范疇。

表3 計算選用網格的數量、近壁面網格尺寸及計算得到的Y＋范圍Table 3 Grid number，dimension of near－wall mesh and range of Y＋

3．1 網格對計算結果的影響

由ANSYS FLUENT14．5理論手冊［13］可知，當湍流模型和增強壁面函數同時使用時，無論是k－ε模型還是k－ω模型對近壁面網格Y＋的要求均降低，為評估該模型，對4套網格分別采用RNGk－ε方程和增強壁面函數進行計算，得到的截面平均空泡份額、流體截面平均溫度、壁面溫度沿軸向高度的分布如圖2所示。由圖2a可看出：對于截面平均空泡份額（VOF），ICM1～3的計算結果與實驗值符合較好；而網格最密的ICM4的計算結果與實驗值偏差較大，采用ICM4計算得到的沸騰起始點晚于實驗值。由圖2b可看出，流體截面平均溫度的計算值均高于實驗值，且隨近壁面網格Y＋的減小，流體截面平均溫度與實驗值的偏差變大；總的來說，ICM1～3計算結果與實驗值符合良好，ICM4計算值與實驗值偏差較大。由圖2c可看出，ICM1、2計算得到的壁面溫度分布與實驗值符合良好，ICM3計算得到的壁面溫度分布在0．25～0．35m高度處呈輕微震蕩，ICM4計算結果在0．1～1．2m高度處呈鋸齒形震蕩，且ICM3、4計算結果與實驗值偏差較大。綜合圖2可得：雖然增強壁面函數可允許k－ε模型的近壁面網格Y＋＜11．225，但由分析結果可看出，對于過冷沸騰計算，當Y＋＜11．225時，與近壁面網格的相關的參數（壁面溫度）出現不合理的鋸齒形震蕩。

圖2 網格對計算結果的影響Fig．2 Effect of grid on calculation result

3．2 湍流模型對計算結果的影響

圖3示出不同湍流模型對計算結果的影響。分析在ICM2的基礎上進行，分別采用標準、可實現、RNGk－ε模型，標準和SSTk－ω模型和增強壁面函數法，采用Mixture、Dispersed、Per Phase方法計算湍流。由計算結果可看出，對于ICM2，所有湍流模型的計算結果與實驗值均符合較好。在圖3a空泡份額的分布中，采用Standard－k－w－EnhancedWF－D方法得到的計算結果與實驗值偏差最大；采用不同模型計算得到的截面流體平均溫度和壁面溫度無明顯區別；采用Dispersed和Per Phase方法時，計算得到的空泡份額較Mixture方法的大。根據文獻［14］，采用Dispersed和Per Phase方法求解湍流模型相較Mixture方法需要更多的計算時間和內存，亦可獲得更高的精度。通過計算分析發現，對于過冷沸騰工況，采用Dispersed 和Per Phase方法計算精度并不比Mixture方法的計算精度高。另外，采用Dispersed和Per Phase方法時計算收斂性降低且計算耗時成倍增加。

3．3 壁面函數對計算結果的影響

圖4為采用不同壁面函數得到的計算結果。由圖4可看出，當近壁面網格滿足壁面函數的要求時，所有的壁面函數均可得到相當高精度的模擬結果。通過對比圖4a中增強壁面函數Dispersed和Mixture方法得到的VOF亦可發現，Dispersed方法得到的VOF較Mixture方法得到的偏大。不同壁面函數得到的流體截面平均溫度無區別。壁面溫度分布稍有不同，采用非平衡壁面函數得到的壁面溫度最低且與實驗值偏差最大；增強壁面函數的計算結果略遜于標準壁面函數和擴展壁面函數的結果，但總體與實驗值符合較好。

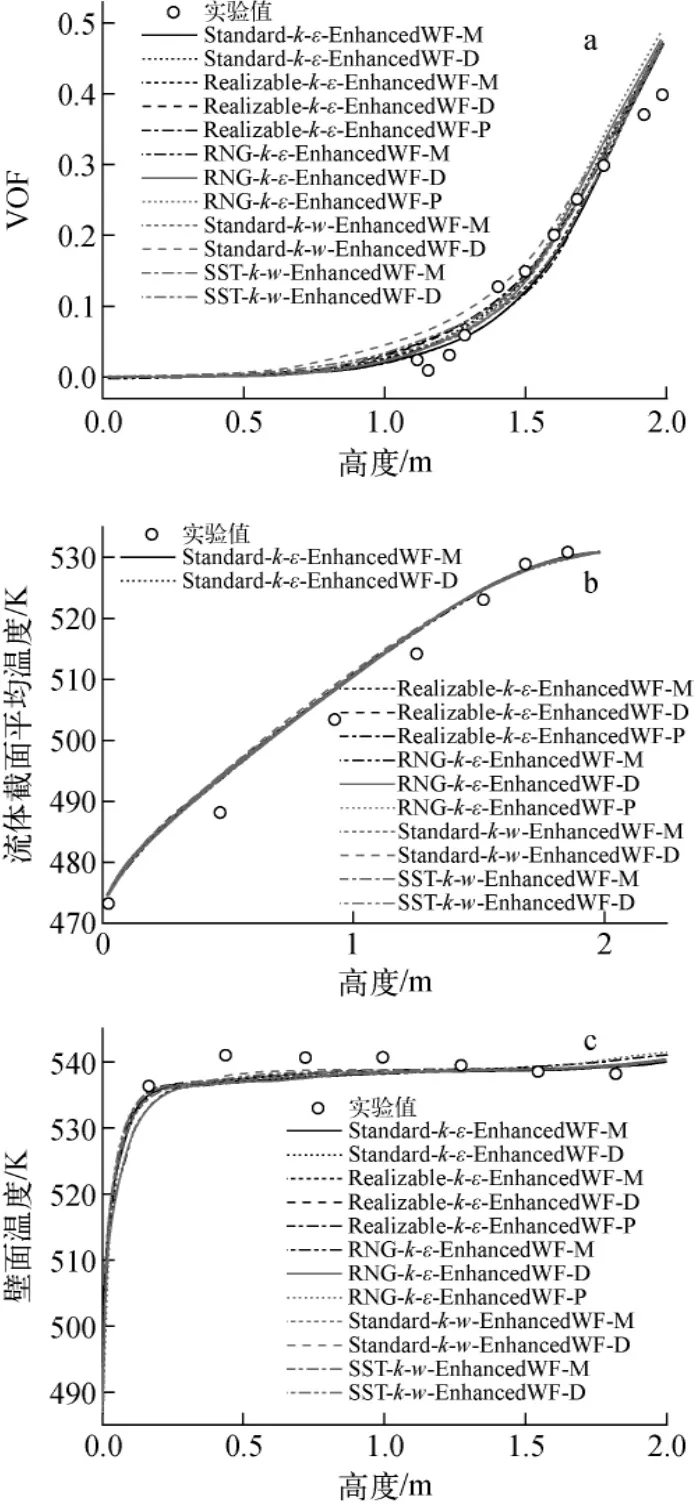
圖3 湍流模型對計算結果的影響Fig．3 Effect of turbulence model on calculation result

3．4 k－ω模型網格依賴性分析

在k－ω模型［15－17］中，k－ω模型需近壁面網格Y＋≈1，而ANSYS FLUENT14．5［14］通過對k－ω模型引入增強壁面函數近壁面處理，使該模型對近壁面網格精度要求降低，允許Y＋≈10～100量級。本文分別在ICM2和ICM4的基礎上采用標準和SSTk－ω模型進行計算，并將計算結果與實驗值進行對比，結果如圖5所示。由圖5可看出，基于ICM2的計算結果與實驗值符合較好，且優于基于ICM4的計算結果。在該計算中，兩套網格的近壁面網格Y＋列于表4。ICM4滿足常規k－ω模型的網格要求［15－17］，但其計算精度卻低于ICM2，且壁面溫度出現不合理的波動。這是由于當近壁面網格太小時，網格內氣泡的瞬時影響無法被時均，從而導致時均計算方法出現波動。

3．5 模型總體性能評價

圖4 壁面函數對計算結果的影響Fig．4 Effect of wall function on calculation result

圖5 網格對k－ω模型計算結果的影響

Fig．5 Effect of grid on calculation result of k－ωmodel

根據文獻［11－13，15－17］，對每組網格分別選取最佳湍流模型（ICM1～3，k－ε；ICM4，k－ω）進行計算，將計算結果與實驗值進行對比，結果如圖6所示。由圖6可看出，對于ICM1～3，基于k－ε模型的計算結果與實驗值符合較好；而對于ICM4，基于k－ω模型的計算結果與實驗值偏差較大。又由圖2可知，對于ICM4，基于k－ε模型的計算結果與實驗值偏差也較大，即無論k－ω還是k－ε模型，ICM4的計算結果與實驗值偏差均大于其他網格。由圖6b可知，ICM1網格、標準k－ε模型計算得到的流體截面平均溫度與實驗值最為接近。由圖6c可知，ICM2網格標準k－ε和可實現k－ε模型的計算壁面溫度與實驗值最為接近。即當近壁面網格Y＋滿足傳統k－ε網格要求（Y＋＞11．225）時，計算結果最優。文獻［13］指出，當引入增強壁面函數之后，近壁面網格越密越能得到更為準確的結果；文獻［18］中通過單相算例證實了這一結論，但在兩相過冷沸騰計算中，過于精細的網格不能得到合理的計算結果。

表4 近壁面網格Y＋Table 4 Near wall mesh Y＋for grid

圖6 各網格配以最佳湍流模型計算結果Fig．6 Result of each mesh with optimized turbulence model

4 結論

本文采用多組網格、多種湍流模型對過冷沸騰基準實驗進行計算，分析湍流模型對過冷沸騰計算的影響，得出如下結論：

1）采用Dispersed方法和Per Phase方法計算兩相的湍流參數，相較Mixture方法，計算收斂性和耗時增大，但計算精度并無明顯提高；

2）當近壁面網格滿足Y＋＞11．225時，采用各種k－ε模型計算結果與實驗值均符合良好且差別不大；

3）采用k－ε模型時，非平衡壁面函數的計算精度較其他壁面函數的低；

4）當Y＋≈1時，增強壁面函數不能獲得滿意的預測計算結果；

5）采用k－ω模型時，近壁面網格Y＋≈1時預測精度較差；

6）對于過冷沸騰數值模擬，k－ε模型的預測精度整體高于k－ω模型。

參考文獻：

［1］ KURUL N，PODOWSKI M Z．On the modeling of multidimensional effects in boiling channels［C］∥Proceedings of the 27th National Heat Transfer Conference．Minneapolis，USA：［s．n．］，1991．

［2］ OSE Y，KUNUGI T．Development of a boiling and condensation model on subcooled boiling phenomena［J］．Energy Procedia，2011，9：605－618．

［3］ KREPPER E，KONCˇAR B，EGOROV Y．CFD modelling of subcooled boiling：Concept，validation and application to fuel assembly design［J］．Nuclear Engineering and Design，2007，237（7）：716－731．

［4］ YAN J，SMITH L D，KAROUTAS Z．Departure from nucleate boiling modeling development for PWR fuel［C］∥2013 21st International Conference on Nuclear Engineering．Chengdu：［s．n．］，2013．

［5］ BARTOLEMEI G G，CHANTURIYA V M．Experimental study of true void fraction when boiling subcooled water in vertical tubes［J］．Thermal Engineering，1967，14（2）：123－128．

［6］ BARTOLEMEI G G，BRANTOV V G，MOLOCHNIKOV Y S，et al．An experimental investigation of true volumetric vapor content with subcooled boiling in tubes［J］．Thermal Engineering，1982，29（3）：132－135．

［7］ ISHII M，ZUBER N．Drag coefficient and relative velocity in bubbly，droplet or particulate flows［J］．AIChE Journal，1979，25（5）：843－855．

［8］ MORAGA F，BONETTO F，LAHEY R．Lateral forces on spheres in turbulent uniform shear flow［J］．International Journal of Multiphase Flow，1999，25（6）：1 321－1 372．

［9］ ANTAL S，LAHEY R，Jr，FLAHERTY J．Analysis of phase distribution in fully developed laminar bubbly two－phase flow［J］．International Journal of Multiphase Flow，1991，17（5）：635－652．

［10］RANZ W，MARSHALL W．Evaporation from drops［J］．Chem Eng Prog，1952，48（3）：141－146．

［11］LAUNDER B E，SPALDING D B．Lectures in mathematical models of turbulence［M］．France：Academic Press，1972．

［12］SHIH T H，LIOU W W，SHABBIR A，et al．A newk－εeddy viscosity model for high reynolds number turbulent flows［J］．Computers ＆Fluids，1995，24（3）：227－238．

［13］ORSZAG S A，YAKHOT V，FLANNERY W S，et al．Renormalization group modeling and turbulence simulations［J］．Near－wall Turbulent Flows，1993：1 031－1 046．

［14］ANSYS FLUENT theory guide［M］．Canonsburg，USA：ANSYS Inc．，2011．

［15］MENTER F R．Two－equation eddy－viscosity turbulence models for engineering applications［J］．AIAA Journal，1994，32（8）：1 598－1 605．

［16］MENTER F，KUNTZ M，LANGTRY R．Ten years of industrial experience with the SST turbulence model［J］．Turbulence，Heat and Mass Transfer，2003，4：625－632．

［17］WILCOX D C．Turbulence modeling for CFD ［M］．CA：DCW Industries La Canada，1998．

［18］ANSYS FLUENT tutorial guide［M］．Canonsburg，USA：ANSYS Inc．，2011．

Effect of Turbulence Model on Prediction of Subcooled Boiling

ZHANG Rui1，2，TIAN Wen－xi1，2，CONG Teng－long1，2，SU Guang－hui1，2，QIU Sui－zheng1，2
（1．State Key Laboratory of Multiphase Flow in Power Engineering，Xi’an Jiaotong University，Xi’an710049，China；2．School of Nuclear Science and Technology，Xi’an Jiaotong University，Xi’an710049，China）

Abstract：The ANSYS FLUENT14．5was employed to simulate the two－phase forced convection subcooled boiling in a vertical heated pipe．Different turbulence models，wall functions and two－phase turbulence treatments were utilized to each of four sets of grids．Results were compared with experiment data to analyze the effects of grids，turbulence model，wall functions and two－phase turbulence treatments．The results of k－εmodel show better agreement with experiment data than those of k－ωmodel．Dispersed and Per Phase treatments for two－phase turbulence parameters perform no better than Mixture treatment．The enhanced wall function can’t achieve satisfactory results for the grid with near wall function Y＋≈1．

Key words：subcooled boiling；turbulence model；calculation accuracy

作者簡介：張 蕊（1990—），女，陜西咸陽人，博士研究生，核能科學與工程專業

基金項目：國家杰出青年科學基金資助項目（11125522）

收稿日期：2014－04－21；修回日期：2014－06－07

doi：10．7538／yzk．2015．49．08．1366

文章編號：1000－6931（2015）08－1366－08

文獻標志碼：A

中圖分類號：TL334