分離式波箔動壓氣體推力軸承壓力場特性研究

賀煥源，馬希直

(南京航空航天大學 機電學院，江蘇 南京 210016)

?

分離式波箔動壓氣體推力軸承壓力場特性研究

賀煥源，馬希直

(南京航空航天大學 機電學院，江蘇 南京 210016)

摘要：分離式波箔氣體軸承是新一代柔性氣體軸承，其承載能力的準確預測是該類軸承性能預測和設計準則確定的基礎，箔片的變形和氣膜壓力的求解是承載能力預測的關鍵。分別采用線性剛度模型和薄板彎曲模型對分離波箔片和平箔片變形進行建模。應用非線性數值求解方法對可壓縮氣體Reynolds方程和變形方程進行氣彈耦合數值求解，獲得了軸承的壓力分布。結果表明分離式波箔片可以提高軸承的承載能力，而平箔片的變形會導致承載能力的降低。通過比較發現計算結果和實驗數據具有較好的一致性。

關鍵詞：氣體動壓推力軸承；分離波箔；靜剛度；變形；承載能力

0前言

波箔軸承因相對承載能力較高，穩定性較好，在國外應用最為廣泛，被成功應用于燃氣渦輪機、透平膨脹機等輕載高速旋轉機械，并取得了良好的經濟效益[1]。與剛性軸承相比，波箔軸承的表面是柔性的，當轉軸上有脈沖波動時，其能量轉換成波箔的彈性變形，吸收轉軸渦動的動能，抑制自激渦動的形成，為軸承穩定工作提供良好的條件[2]。軸承運轉時，氣膜壓力導致箔片結構發生變形，箔片變形引起氣膜厚度的改變，氣膜厚度改變反而又會引起氣膜壓力分布的改變，如此循環迭代，直到氣膜壓力和氣膜厚度都達到穩定[3]。建立波箔軸承物理模型的關鍵在于應用合理的模型來描述箔片結構的阻尼和剛度。

國外學者對此進行了大量的工作，為解決箔片軸承的氣彈耦合問題做了突出的貢獻。Walowit的理論研究了單個波箔結構，忽略了平箔和波箔之間，波箔片和軸承座之間的庫倫摩擦力，不考慮各箔拱之間相互作用力的影響。Heshmat在Walowit的基礎之上提出了簡單的彈簧基礎模型，這種模型耦合了支撐波箔變形和氣膜動態壓力，波箔的彈性變形和壓力成正比，波箔片的變形系數取決于波箔片的幾何結構、材料和厚度。單個箔拱物理簡化模型如圖1所示。圖中PL為氣膜絕對壓力，Pa為波箔環境壓力，通常情況下為大氣壓力，b為箔拱阻尼，wb為波箔片位移，kb為單個箔拱結構剛度。

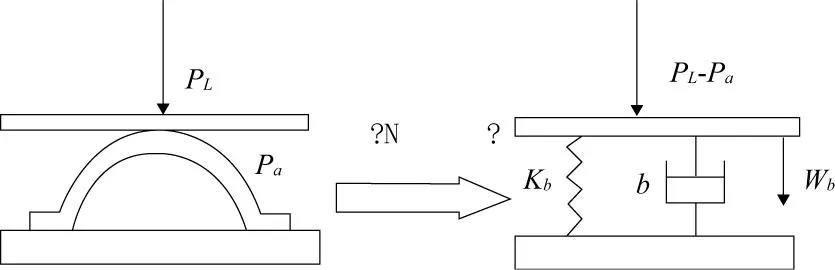
圖1　波箔片彈簧基礎模型

圖2　分離式波箔片和整體式波箔片

分離式波箔片和整體式波箔片如圖2所示，分離式波箔由沿半徑方向分離的若干箔帶構成，每條箔帶上分布不同節距的箔拱，相鄰箔帶上的箔拱相互錯開。分離式箔片沿半徑方向和圓周方向剛度均可變化，這種剛度特性有助于軸承適應沿半徑方向線速度差異導致的壓力分布不均，從而能夠均勻化壓力，協調箔片變形，提高軸承承載能力[4]，箔帶之間的狹縫使得波箔片避免了由于溫度分布不均引起的熱變形，此外還能夠使軸承適應少量的軸向偏斜。

目前國內外對整體式波箔軸承特性分析較多，而對分離式波箔軸承研究較少。為了研究這種分離式波箔軸承壓力分布特性，本文采用Heshmat線性剛度模型和薄板彎曲變形方程分別計算了波箔和平箔變形，通過氣彈耦合對該種軸承的氣膜壓力場分布規律及承載能力進行了研究。

1物理模型的建立

1.1　壓力控制方程

由流體力學潤滑基本方程中的N-S方程和連續性方程可得到極坐標系下定常流動Reynolds壓力控制方程：

(1)

式中：p為氣膜壓力，h為氣膜厚度，μ為氣體動力粘度，ω為推力盤相對軸承轉速，r和θ分別為扇形箔片區域內的極坐標。

1.2　 氣膜厚度方程

氣膜厚度分布如圖3所示，通過分析扇形箔片的幾何形狀可得到氣膜厚度表達式[5]：

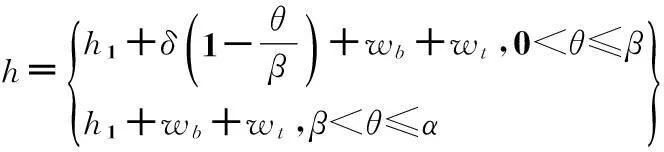
(2)

圖3　氣膜厚度分布

式中：h1為平箔片平行面區氣膜厚度，δ為平箔片斜面區高度，β為平箔片斜面區終止角。

箔片受力示意圖如圖4所示，tp為平箔片厚度，tb為波箔片厚度，l為半箔拱距，s為箔拱節距。在忽略摩擦的條件下單個箔拱結構剛度kb可以由式(3)[6]表示。

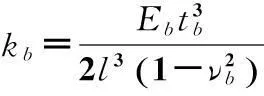
(3)

式中：Eb為波箔片材料彈性模量，νb為波箔片材料泊松比。

圖4　箔片受力

單位長度的波箔節距內波箔片的變形方程為：

(4)

對于定常流動不用考慮結構阻尼的影響，則上述方程可變為：

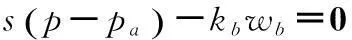
(5)

從以上方程可以得出波箔變形公式：

(6)

以上方程是在以下假設條件下得出：

1)單個箔拱結構剛度kb在整個扇形瓦片范圍內為常數，不隨載荷的變化而變化。

2)平箔片隨波箔片一起變形，但不考慮平箔片局部的彎曲變形。

3)波箔片任意一點的變形大小與該點的受力相關。

對于以上假設，國內外眾多學者認為不考慮平箔片在氣膜壓力作用下的彎曲變形是不符合實際情況的，因此有必要將平箔片變形考慮到氣膜厚度方程中。由薄板單元的彎曲變形方程可以得到平箔的變形表達式[7]，其中s,x的含義見圖4，Dt為平箔彎曲剛度，Et為平箔片材料彈性模量，νt為平箔片材料泊松比。

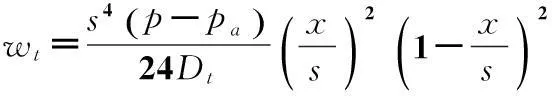
(7)

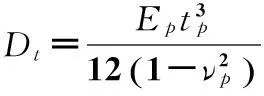
(8)

2計算結果分析

對經過有限差分離散后的壓力方程和膜厚方程，通過超松弛迭代(SOR)實現耦合求解，本文采用MATLAB語言編程實現迭代。為了驗證數值求解的正確性，軸承運行參數和結構參數均選用國外文獻中的參數[8]，以便和國外實驗結果進行比較。數值求解壓力分布圖如圖5和圖6所示：

圖5　整體式波箔軸承氣膜壓力分布

圖6　分離式波箔軸承氣膜壓力分布

圖5和圖6分別給出了分離式波箔軸承和整體式波箔軸承在平箔片平行區氣膜厚度為10μm，轉速為23000r/min時的三維氣膜壓力分布圖。從以上兩圖中可以看出：分離式波箔軸承在平箔片平行區壓力分布更為平緩[9]，從而使得其相對整體式波箔軸承具有更高的穩定性；由于平箔片局部的彎曲變形，在產生彎曲變形的區域壓力局部減小，氣膜產生二次動壓效應；整體式波箔軸承在相鄰兩個箔拱之間形成一條貫穿半徑方向的通道，導致更多的高壓氣體從端部泄露出去，分離式波箔軸承泄氣通道沿半徑方向被箔拱錯開，減少了箔片中間高壓氣體端部泄露，因為承載能力得到了提高。

將氣膜壓力在平箔片區域內進行積分，可得到氣膜對整個軸承產生的承載力為：

(9)

將彈性波箔氣膜壓力帶入到式(9)中得到軸承承載力的理論值為121N，NASA實驗室Brian Dykas的實驗結果為125N。可以看出，數值模擬結果和實驗結果非常接近，說明本文采用的剛度模型和數值計算方法是可信的。在不同轉速下分別計算剛性軸承、整體式波箔軸承和分離式波箔軸承承載力，如圖7所示。

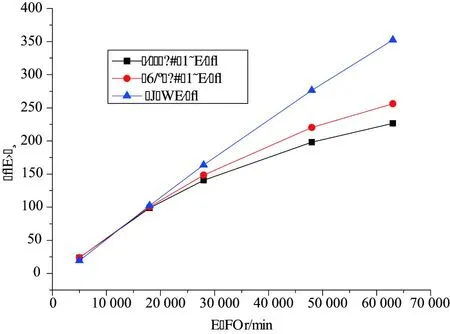
圖7　轉速和承載力的關系

分析圖7中承載力曲線特征可以得到：在低速階段，整體式波箔軸承和分離式波箔軸承比剛性軸承具有更高的承載力，即彈性表面軸承具有更好的低速適應性；隨著轉速的升高，整體式波箔軸承和分離式波箔軸承承載力下降到剛性軸承承載力以下，但是彈性表面軸承比剛性軸承具有較好的穩定性，分離式波箔軸承在保持較好的穩定性的前提下，其承載能力相對整體式波箔軸承有所提高。

3結論

1) 分離式波箔片相鄰兩箔帶之間相互錯開的箔拱結構，減少了高壓氣體的端部泄露，使得分離式波箔軸承在保持軸承運轉穩定性的前提下，提高了軸承承載力。

2) 將波箔剛度等價為彈簧模型是可行的，彈簧模型可以使問題的簡化，易于實現氣彈耦合迭代，通過理論值和實驗值的比較，可以證明物理模型和求解方法的正確性。

3) 由于平箔片的彎曲變形，使得整體式波箔軸承和分離式波箔軸承氣膜壓力整體下降，并且產生二次動壓現象。

參考文獻:

[1] Christopher W, Antonio R Zaldana. A System Approach to the Slid Lubrication of Foil Air Bearings for Oil-free Turbomachinery [J]. ASME, Tribol.2004, 126: 200-207.

[2] 劉占生,許懷錦. 波箔型動壓氣體徑向軸承的應用與研究進展[J]. 軸承, 2008, 01: 39-43.

[3] 徐潤,馬希直. 基于彈性殼體模型的波箔式氣體動壓徑向軸承靜特性分析[J]. 潤滑與密封, 2010, 35(1): 17-21.

[4] Heshmat H. Advancements in the performance of aerodynamic foil journal bearings: High speed and load capability [J]. Tribology Transactions, 1996, 116(2): 287-295.

[5] Yong Bok Lee, Tae Young Kim. Thrust Bump Air Foil Bearings with Variable Axial Load: Theoretical Predictions and Experiments [J]. Tribology Transactions, 2011, 54: 902-910.

[6] Heshmat H, Walowit J A, Pinkus O. Analysis of Gas-lubricated Foil Journal Bearings. ASME. Tribol, 1983, 105: 647-655.

[7] Walowit J A, Anno J N. Modem Developments in Lubrication Mechanics [M]. London: Applied Science Publisher Ltd., 1975.

[8] Brian D, Robert B. Design, Fabrication, and Performance of Foil Gas thrust Bearings for Microturbomachinery Applications [J]. ASME, Journal Engineering for Gas Turbines Power, 2009, 131: 012301-1.

[9] 周權,侯予等.基于有限差分法的動壓氣體止推軸承靜特性分析[J]. 潤滑與密封, 2009, 34(8): 6-9.

Characteristic Research on Pressure Fields of Separation-type Bump Foil Hydrodynamic Thrust Bearings

HE Huan-yuan, MA Xi-zhi

(Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:Separation-type bump foil bearing is a new type gas thrust bearing. The method of accurately predicting the load capacity of bump foil gas bearing is the basis on which its forecast and design principles are realized. The key of the prediction is to resolve foil deformation and pressure . Linear spring model and bending deformation equation of plate are used to calculate deformation of bump foil and top foil respectively. Gas pressure distribution is numerically solved by coupling through Reynolds equation and elastic deformation equation. The result shows that the top foil deformation reduces load capacity, however the separation structure can increase load capacity. The numercal results show good agreement with experimental data.

Keywords:hydrodynamic thrust bearings; separation-type bump foil; static stiffness; deformation; load capacity

中圖分類號：TH133.3

文獻標志碼：A

文章編號：1671-5276(2015)02-0004-03

作者簡介：賀煥源——