砂土材料狀態相關臨界狀態各向異性模型

李學豐，袁琪，王 興

（寧夏大學 固體力學研究所，銀川 750021）

砂土的力學響應與其材料狀態緊密相關［1－3］。傳統本構理論往往忽略了材料狀態對應力－應變關系的影響，將不同孔隙比同一種砂視為不同的材料，使得同一種砂必須使用多組材料參數才能描述其力學特性，相對繁雜，存在一定的局限性。材料狀態相關臨界狀態理論則能有效克服這些局限性［4－7］。

砂土材料狀態不僅要考慮其相對密度、有效圍壓，還要考慮其細觀各向異性和應力加載方式。這幾個因素的相互影響造成了砂土強度－變形的復雜性。在這個復雜變化過程中實質變化的是材料細觀狀態，因此，結合其細觀狀態研究力學特性逐步引起關注［8－14］。Mooney等［8］用攝影技術研究剪切帶的演化規律時發現了臨界狀態線在e-p平面不唯一。Yoshimine［9］、Nakata等［10］的大量試驗逐步也證實了臨界狀態線不唯一，其不唯一的根本原因是砂土初始各向異性的存在。Dafalias［11］最早應用該特性建立粘性土的本構關系。對于砂土，Wan等［12］、Li等［13］和Dafalias等［14］許多學者都根據砂土臨界狀態的不唯一性建立了本構關系。考慮臨界狀態不唯一建立本構的關鍵是對土體細微觀結構與材料狀態關系的合理描述。最近，Li等［15］、Zhao等［16］、Abouzar等［17］對砂土細觀組構對臨界狀態不唯一關系進行了研究，為合理描述砂土各向異性力學特性奠定了基礎，也為材料狀態相關臨界狀態理論提供了新思路。

為合理描述各向異性砂土的強度－變形特性，在黃茂松等［6－7］模型及砂土各向異性分析［18］的基礎上，在材料狀態相關臨界狀態理論的框架下，基于砂土臨界狀態的不唯一，考慮其細觀組構對材料臨界狀態、峰值狀態、相變狀態、剪脹性及其硬化規律的影響，建立各向異性砂土的本構模型，期望逐步實現砂土細觀結構對宏觀力學特性影響的定量描述。

1 砂土各向異性對材料狀態的影響

臨界狀態理論基于粘性土試驗提出，很好描述了粘性土的臨界特性。對于砂土，許多試驗表明其臨界應力比與孔隙比關系不唯一，根本原因是其各向異性的存在。

1.1 砂土各向異性臨界狀態描述

試驗表明砂土的臨界狀態線在e-lnp平面不是直線，這與粘性土有很大的差別。Li等［4］通過對砂土試驗的歸一化得到表達式為

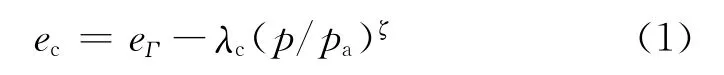
式中：eΓ、λc和ζ為決定臨界狀態線的材料參數；p為當前平均應力；pa為大氣壓力，如圖1。式（1）是圍壓的函數，不同圍壓下，各向同性砂有唯一的臨界狀態線，不同的相變線。臨界狀態是不同圍壓下相變狀態的臨界值［2］。

圖1 Toyoura砂相變狀態線與臨界狀態線 （文獻［2］）Fig.1 Phase transformation and Critical-state lines of Toyoura

當各向異性存在時，砂土臨界狀態不唯一。考慮各向異性對砂土臨界狀態線影響的時，式（1）中eΓ、λc和ζ都要受各向異性的影響。然而，同時考慮3個參數的影響，將會極大增加本構描述的復雜性。Poulo等［19］研究認為砂土顆粒排列主要對其臨界狀態線斜率影響最大，基于這個研究成果Li等［13］提出的臨界狀態線只考慮eΓ影響，Yang等［20］通過細觀試驗又做了相應的改進。Abouzar等［17］針對組構對π平面臨界狀態特性的研究很好解決了這個問題。基于以上分析和筆者的各向異性破壞特性［19］方面的工作，將文獻［19］新定義的狀態變量引入式（1）建立了臨界狀態線

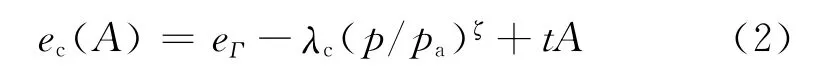
式中：t是狀態參數，式（2）在ec－（p／p）ζ平面內變為相互平行的直線，t可以由常規三軸壓縮、伸長試驗由式（2）直線截距差得到，本文使用Yang等［21］結合Toyoura砂細觀定量檢測的三軸試驗確定；A為是筆者等在文獻［19］中定義一個新的各向異性狀態變量

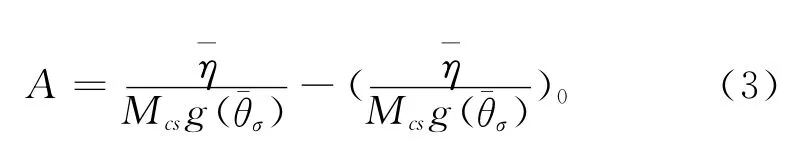
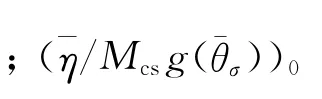
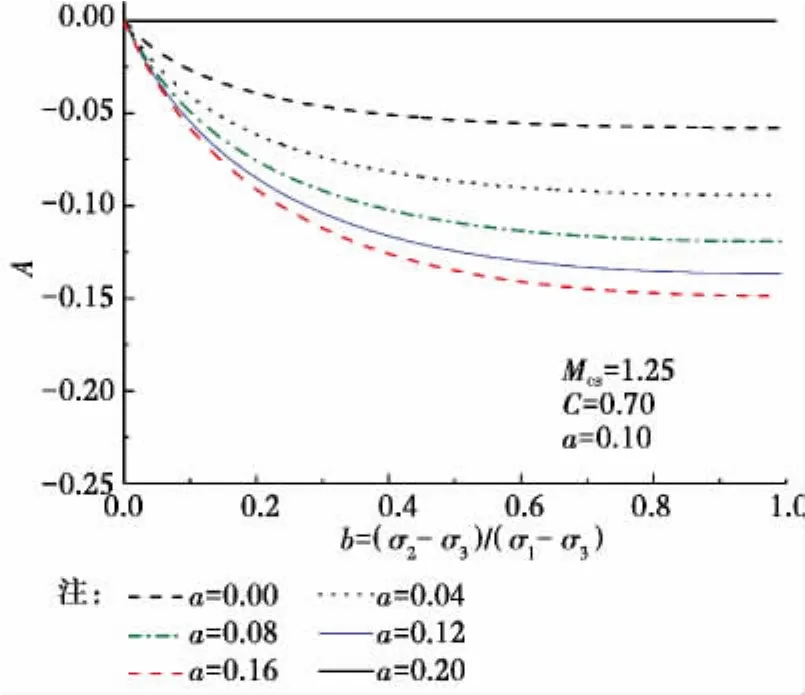
圖2 狀態變量A與中主應力系數的關系Fig.2 Anisotropic state variable VS Intermediate principal stress coefficient.

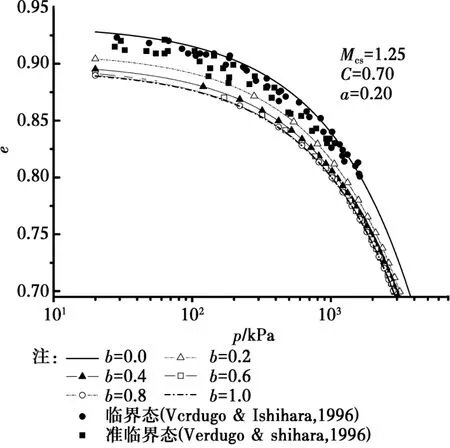
圖3 各向異性臨界狀態線Fig.3 Anisotropic Critical-state lines

式（2）是A的函數，A受應力狀態、各向異性程度和應力與土體組構角度3個因素的影響，因此，隨3個因素的變化會導致式（2）的變化，直接導致臨界狀態線的不唯一。如圖3所示，其它材料參數保持不變時，材料為各向同性時，A恒等于零，A對式（2）沒有影響；當a＝0.2時（A的變化如圖2），臨界狀態線隨中主應力系數b的變化在一定區間變化，這個區間為Verdugo等［2］通過試驗得到Toyoura砂的準臨界狀態和臨界狀態區間。

1.2各向異性臨界狀態線的特點

現有試驗成果表明各向異性對砂土臨界狀態的影響主要表現在e-（p／pa）ζ平面、π平面上和摩爾圓平面上的影響規律。

1）根據式（2）可以直觀地看出，在e-（p／pa）ζ平面上，臨界狀態線是各向異性狀態變量的函數，其斜率受砂土各向異性程度、應力狀態以及組構與應力的幾何關系3個主要因素的影響，臨界狀態線是相互平行的直線。

2）根據材料狀態相關臨界狀態理論，考慮各向異性后，臨界狀態應力比的一般表達式為

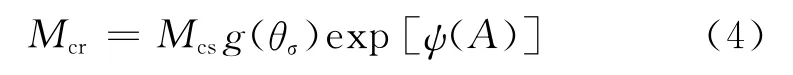
式中：Mcs為常規壓縮三軸試驗確定的臨界狀態應力比；ψ（A）是考慮各向異性的狀態參量。根據Been等［1］定義狀態參數，增加了各向異性對狀態參數的影響，其表達式為

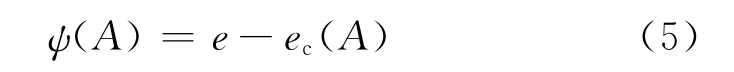
式中：e為當前孔隙比為ec（A）為式（2）定義的各向異性臨界狀態線。土體達到臨界狀態時，必須滿足孔隙比和應力比分別同時達到臨界狀態孔隙比和臨界應力比兩個基本條件。則式（5）可以表示為

式（6）和文獻［19］破壞準則形式一致，因此，在π平面上表現的各向異性特性和各向異性破壞規律相似。如圖4所示，在π平面上，臨界狀態線的形狀和位置都受各向異性的影響。各向異性時，其中心自然偏離了靜水壓力軸，而且各向異性越大，偏離靜水壓力軸中心越遠，同時其形狀改變也越大。在常規三軸壓縮點（圖中與σ1軸的交點）各向同性和各向異性值相同，定義A采用了基準點的思想很好描述了這個特性，這與文獻［21］的試驗結論一致。圖4中峰值線和相變狀態線也具有以上特點。結合圖1，臨界狀態是相變狀態的極限表現，合理描述臨界狀態的各向異性對砂土本構的峰值狀態和相變狀態有重要作用。

圖4 π平面上的狀態線Fig.4 State line on the octahedral plane.

3）在同一孔隙比和應力狀態的條件，式（2）定義可以較好描述隨砂土沉積角度變化土體臨界狀態值的試驗規律。如圖5所示，當砂土的沉積面方向和小主應力軸為90°時，臨界狀態強度最大，0°時到最小值，隨沉積面角度變化臨界強度單調遞減。這個規律和Oda等［22］等的真三軸試驗結果一致。

綜上所述，臨界狀態線能較好描述各種空間、應力狀態和各向異性程度砂土臨界狀態變化規律。

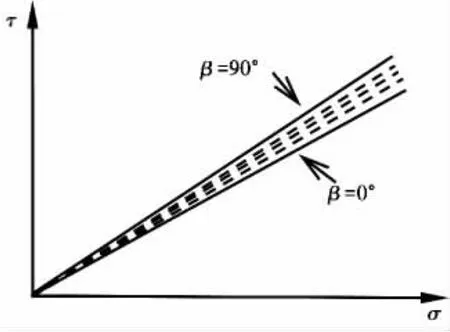
圖5 摩爾圓平面上的各向異性臨界狀態線Fig.5 Anisotropic Critical-state lines on the Mohr plane.

2 模型框架

2.1 屈服面

屈服面采用式（7）所示形式。

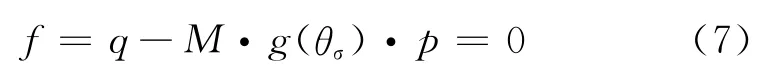
式中：M為硬化內變量；g（θσ）為羅德角的插值函數，采用 William等［23］建議的橢圓形插值函數。

2.2 剪脹性

剪脹性不僅與孔隙比和圍壓有關，同時，也受砂土初始各向異性的影響。參考Gajo等［24］提出的剪脹方程并考慮各向異性的影響，將方程修正為

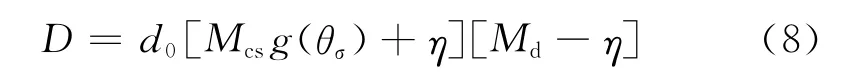
式中：d0為模型參數；Md為狀態轉換應力比。試驗結果表明：Md不是常量，而是與材料狀態相關。Md參考Li等［13］建議的形式，本文Md三維空間的表達式為

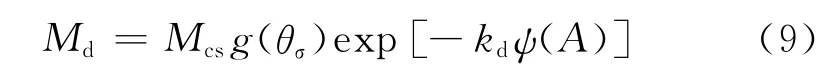
式中：kd模型參數，同樣從式（3）可以看出Md是各向異性狀態變量的函數。如圖1和圖5所示，Md通過狀態參數將材料的當前狀態和臨界狀態緊密聯系起來，式（8）描述的剪脹性也是A的函數。

當砂土為各向同性時，臨界狀態性唯一，其剪脹和剪縮關系也唯一。如圖6（a）所示，當前孔隙比小于臨界應力比砂土特性表現為剪脹，反之為剪縮，其關系唯一；當砂土為各向異性時，由于臨界狀態線不唯一，其剪脹和剪縮特性不唯一。如圖6（b）所示，考慮各向異性后，臨界狀態線受各向異性大小、應力狀態和應力與組構幾何關系3個關鍵因素的影響，臨界狀態線不唯一，為相互平行的直線。對于圖6（a）中狀態A′和狀態B′，在各向同性條件下分別表現為減縮和剪脹的點，然而圖6（b）則分別表現為剪脹和減縮。可以看出，當考慮各向異性對材料狀態的影響后，剪脹性關系的判斷將更加全面、細致。當ψ（A）＞0時表示砂土處于松散狀態，受力會發生剪縮現象，ψ（A）＜0則表示砂土處于密實狀態，受力會發生剪脹現象，而且｜ψ（A）｜大小可以反映剪脹性的大小。ψ（A）通過各向異性狀態變量，也將砂土的各向異性程度、應力狀態和砂土組構與應力之間的關系對砂土剪脹性的影響進行了量化。因此，引入各向異性狀態變量，既豐富了砂土材料狀態描述，又豐富了其剪脹性描述。

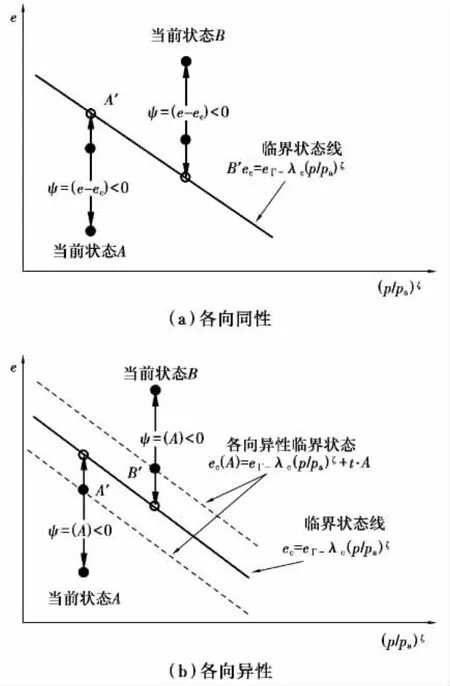
圖6 狀態參量與剪脹的關系Fig.6 Relation between the state parameter and dilatancy

2.3 硬化規律

關于內變量M的硬化規律，采用Li等［25］建議的增量雙曲線形式

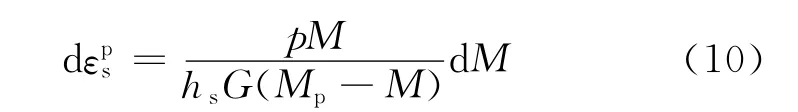
式中：G為彈性剪切模量；hs為模型參數，hs＝（h1－h2e），h1和h2為模型常數；Mp為峰值應力比；hs和Mp都是各向異性狀態變量的函數。模型參數會受各向異性影響的表達式為

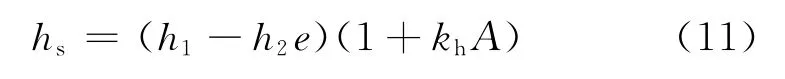
式中：kh為模型參數。

峰值應力比受各向異性影響的表達式為

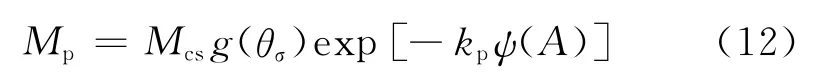
式中：kp是模型參數。從式（12）可以看出峰值應力比也是應力狀態、各向異性參量以及應力和組構張量的幾何關系3個因素的函數。3個因素中各向異性程度對另外兩個因素有實質性影響，各向同性時，A≡0，式（12）只是應力狀態的函數，自然退化為各向同性的形式；各向同性時，各向異性影響規律與本文各向異性對砂土臨界狀態影響相似。對于同一孔隙比、相同各向異性的砂，在同一圍壓條件下，峰值應力隨砂土組構方向與主應力方向的幾何關系相關，隨幾何關系的變化，峰值應力也不斷變化，這種變化可以描述考慮主應力軸旋轉的硬化內變量規律。可見，考慮各向異性后，砂土的峰值應力比描述更加豐富，同時硬化規律的描述也更全面。

綜合式（6）、式（9）和式（12）可以看出：砂土的臨界狀態、峰值狀態和相變狀態都是A的函數。通過A將砂土的細觀結構和宏觀現象聯系起來，砂土細觀參量、細觀組構與應力狀態幾何關系的變化直接描述了宏觀力學特性的變化。如圖4所示，材料為各向同性時，3種狀態在π平面上為軸對稱的各向同性規律；當考慮砂土的各向異性時，各向異性明顯影響了3個狀態線在π平面上的形狀和位置。

3 模型參數確定與驗證

3.1 模型參數的確定

各向異性模型參數主要涉及兩個參數，即各向異性參量a和模型參數t。這兩個參數都反映了砂土的細觀組構特性對宏觀力學特性影響，需要用宏細觀結合的試驗確定。Yang等［20］的Toyoura砂細觀定量分析表明：落砂法觀測的幅值參量平均值為a＝0.214、濕搗法為a＝0.091。參照該試驗成果，本文取a＝0.12。參數t為臨界狀態的試驗參數，它的確定需要結合細觀實驗，用常規三軸壓縮、伸長試驗臨界狀態線確定，如式（2）。根據 Yang等［20］試驗，兩種制樣方法得到的值取平均值后得到t＝0.26。其余模型參數與黃茂松等［6］模型參數一致，模型驗證參數是根據Verdugo等［2］Toyoura砂試驗確定，另外13個模型參數和文獻［7］的模型參數表中參數一致。

3.2 模型參數驗證

對于a和t兩個參數的驗證見文獻［6］。本文用這組參數對砂土不同沉積面角度三軸試驗強度進行驗證。圖7為Lam等［26］真三軸試驗結果，試驗采用Toyoura砂，撒砂法制樣，e＝0.71，圍壓98 k Pa，用相同圍壓對3種試樣進行試驗，試樣分別為H／W＝0.25、H／W＝1.00和H／W＝2.00。該試驗沒有砂土細觀觀測結果，參考Yang等［20］細觀試驗，取a＝0.12。如圖7所示，3種試樣尺寸在相同圍壓條件下，強度隨沉積面角度的變化規律都相似，即隨沉積面角度變化強度單調減小，試驗得到90°和0°時強度相差4°左右。圖7中的模擬可以看出各向異性參數可以較好模擬隨砂樣沉積面角度不同強度的變化規律，模擬的最大值和最小值的變化略小于試驗值。通過試驗模擬再次驗證了各向異性參數的有效性。

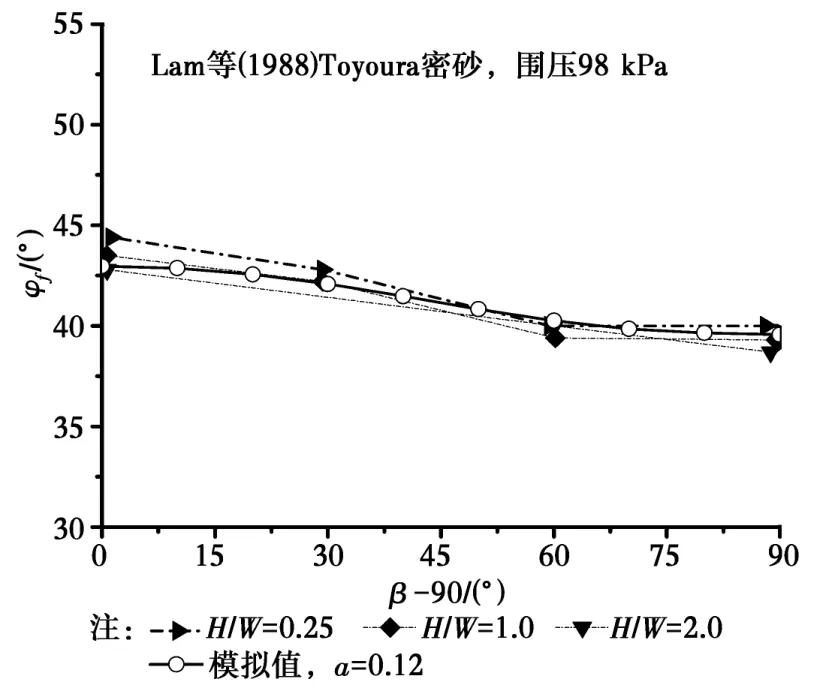
圖7 各向異性砂土的內摩擦角試驗模擬Fig.7 Simulation of the peak friction angle for anisotropic sand

3.3 各向異性對強度的影響

圖8 三軸壓縮不排水試驗與模型模擬對比Fig.8 Comparison between undrained triaxial compression test results and model responses

圖9 三軸伸長不排水試驗與模型模擬對比Fig.9 Comparison between undrained triaxial extension test results and model responses

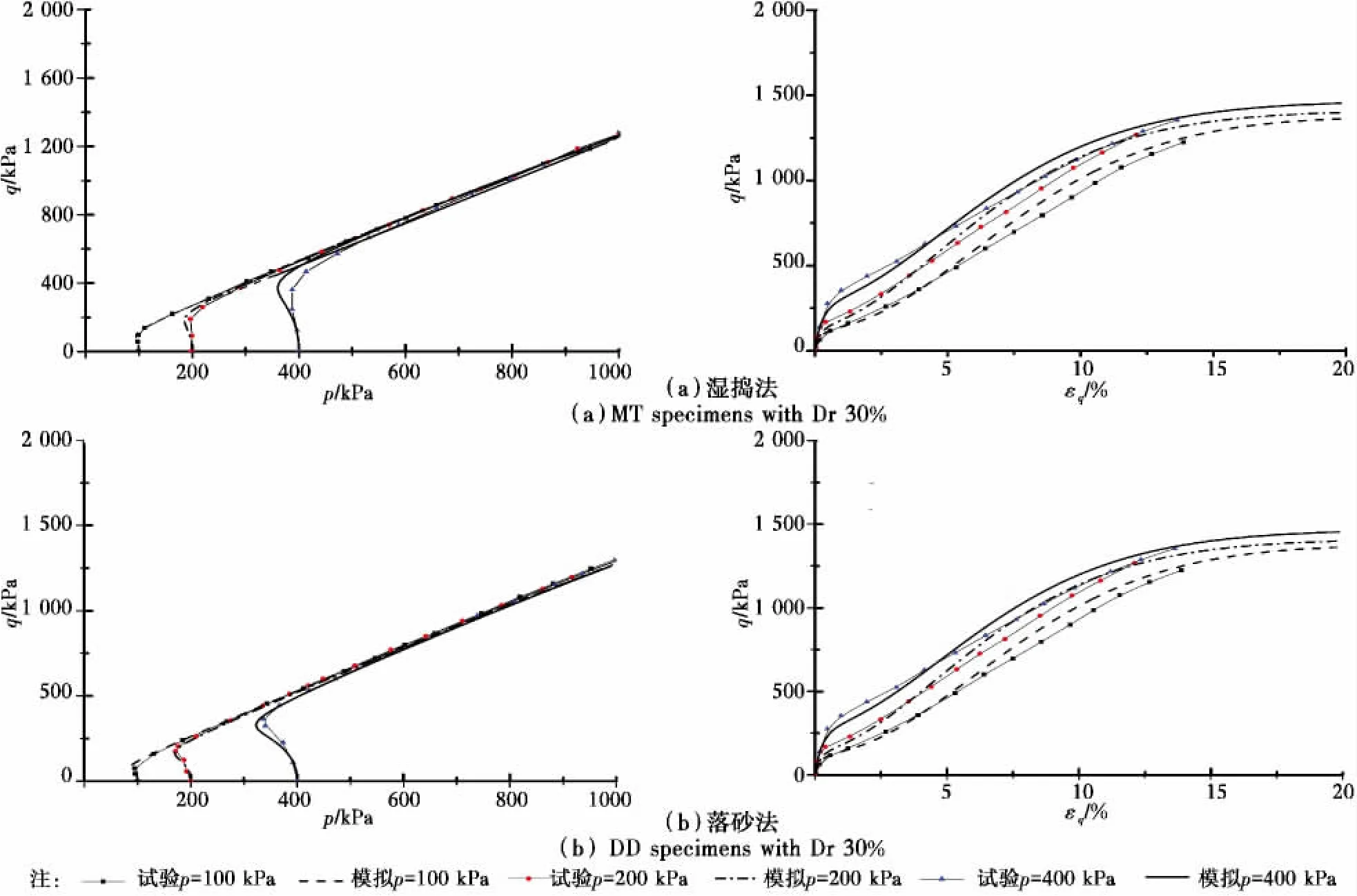
圖10 三軸壓縮不排水試驗與模型模擬對.Fig.10 Comparison between undrained triaxial compression test results and model responses

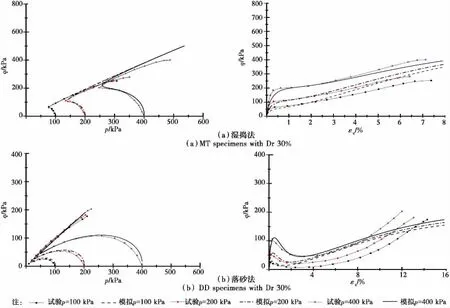
圖11 三軸伸長不排水試驗與模型模擬對比Fig.11 Comparison between undrained triaxial extension test results and model responses

圖8至圖11是Yang等［17］試驗結果和本文模型模擬的對比。通過模擬可以看出，模型可以較好描述試驗初期砂土表現的剪縮性、接近狀態轉化線則表現剪脹性特點。圖10和圖11是三軸拉伸試驗和模型模擬結果。模型對落砂法試樣表現的剪縮軟化特性、濕搗法試樣表現的流動特性、最終出現頸縮特性都能較好描述。圖8至圖11的模擬情況表明，模型可以用一套模型參數，結合細觀定量得到的關系異性參數即可較好模擬各向異性砂土的試驗應力－應變－強度特性，初步驗證了宏細觀結合方法描述砂土特性的合理性。

4 結語

考慮砂土各向異性對其臨界狀態的影響，建立了砂土的各向異性本構模型，并做了模型試驗驗證。

將新的各向異性狀態變量引入砂土的臨界狀態方程后，可以綜合考慮材料的孔隙比、圍壓、應力狀態和各向異性等狀態相關量對材料狀態的影響。擴展了砂土材料狀態相關的描述范圍。

引入狀態變量后，模型能夠較好描述π平面上各向異性砂的臨界狀態、相變狀態和峰值狀態的變化規律。各向異性越大，形狀變化也越大，狀態面偏離的靜水壓力軸也越遠；各向同性時，3個狀態面自然退化到各向同性狀態。模型可以自然描述砂土細觀狀態量的引起宏觀剪脹特性的變化，量化了砂土物理狀態量變化對剪脹性及硬化規律的影響。

［1］Been K，Jefferies M G.A state parameter for sands［J］.Geotechnique，1985，35（2）：99-112.

［2］Verdugo R，Ishihara K.The steady state of sandy soil［J］.Soils and Foundations，1996，36（2）：81-91.

［3］Cai Z Y，Li X S.Deformation characteristics and critical state of sand ［J］. Chinese Journal of Geotechnical Engineering，2004，26（5）：697-701.

［4］Li X S，Dafalias Y F，Wang Z L.State-dependent dilatancy in critical-state constitutive modeling of sand［J］. Canadian Geotechnical Journal，1999，36：599-611.

［5］Yao Y P，Sun D A，Luo T.A critical state model for sands dependent on stress and density ［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2004，28：323-337.

［6］黃茂松，李學豐，賈蒼琴.基于材料狀態相關理論的砂土雙屈服面模型［J］.巖土工程學報，2010，31（11）：1764-1771.

Huang M S，Li X F，Jia C Q.A double yield surface constitutive model for sand based on state-dependent critical state theory ［J］. Chinese Journal of Geotechnical Engineering，2010，31（11）：1764-1771.（in Chinese）.

［7］黃茂松，李學豐，錢建固.各向異性砂土的應變局部化分析［J］.巖土工程學報，2012，34（10）：1885-1892.

Huang M S，Li X F，Qian J G.On Strain localization of anisotropic sands ［J］. Chinese Journal of Geotechnical Engineering，2012，34（10）：1885-1892.（in Chinese）.

［8］Mooney M A，Finno R J，Viggianii G.A unique critical state for sand［J］.Journal of Geotechnical and Geoenvironmental Engineering，1998，124 （11）：1128-1138.

［9］Yoshimine M，Ishihara K，Vargas W.Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand ［J］.Soils and Foundations 1998，38（3）：179-188.

［10］Nakata Y， Hyodo M， Murata H，et al.Flow deformation of sands subjected to principal stress rotation［J］.Soils and Foundations，1998，38 （2）：115-128.

［11］ Dafalias Y F. Bounding surface plasticity I：Mathematical foundation and hypoplasticity ［J］.Journal of Engineering Mechanics，ASCE，1986，112（12）：966-978.

［12］Wan R G，Guo P J.A pressure and density dependent dilatancy model for granular materials［J］.Soils and Foundations，1999，39（6）：1-12.

［13］Li X S，Dafalias Y F.Constitutive modelling of inherently anisotropic sand behavior ［J］.Journal of Geotechnical and Geoemvironmental Engineering，ASCE，2002，128（10）：868-880.

［14］Dafalias Y F，Papadimitriou A G，Li X S.Sand plasticity model accounting for inherent fabric anisotropy ［J］.Journal of Engineering Mechanics，2004，130（11）：1319-1333.

［15］Li X S，Dafalias Y F.Anisotropic critical state theory：the role of fabric ［J］.Journal of Engineering Mechanics，ASCE，2012，138（3）：263-275.

［16］Zhao J，Guo N.Unique critical state characteristics in granular media considering fabric anisotropy ［J］.Geotechnique，2013，63（8）：695-704.

［17］Sadrekarimi A，Olson S M.Residual state of sands［J］.Journal of Geotechnical and Geoemvironmental Engineering，ASCE，2014，128（10）：868-880.

［18］李學豐，黃茂松，錢建固.宏細觀結合的砂土各向異性破壞準則［J］.巖石力學與工程學報，2010，29（9）：1885-1892.

Li X F，Huang M S，Qian J G.Failure criterion of anisotropic sand with the method of macro-micro incorporation［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29 （9）：1885-1892. （in Chinese）

［19］Poulos S J，Castro G，France J W.Liquefaction evaluation procedure ［J］.Journal of Geotechnical Engineering，ASCE，1985，111（6）：772-792.

［20］Yang Z X，Li X S，Yang J.Quantifying and modelling fabric anisotropy of granular soils［J］.Geotechnique，2008，58（4）：237-248.

［21］Ishihara K.Liquefaction and flow failure during earthquakes［J］.Geotechnique，1993，43（3）：351-415.

［22］Oda M，Koishikawa I，Higuchi T.Experimental study on anisotropic shear strength of sand by plane strain test［J］.Soils and Foundations，1978，18（1）：25-38.

［23］William K J，Warnke E P.Constitutive model for the triaxial behavior of concrete ［C］／／International Association for Bridge and Structure Engineering Proceedings，Bergamo，Italy，1975，19：117-131.

［24］Gajo A，Muir W D.A kinematic hardening constitutive model for sands：the multiaxial formulation ［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1999，23：925-965.

［25］Li X S，Daflias Y F.Dilatancy for cohesionless soils［J］.Geotechnique，2000，50（4）：449-460.

［26］Lam W K，Tatsuoka M.Effect of initial anisotropic fabric andσ2on strength and deformation characteristics of sand ［J］.Soils and Foundations，1988，28（1）：89-106.

（編輯王秀玲）