混合算法在鋼構企業生產調度系統中的應用

雷兆明，佟靜翠 ，花季偉，郭子超

（1.河北工業大學 控制科學與工程學院，天津 300130；2.天津師范大學 計算機與信息工程學院，天津 300387）

企業的生產管理系統越來越受到企業的廣泛關注，而合理的生產調度系統是保證企業長期規劃順利、順暢實施的關鍵所在[1]。因鋼結構產品的很多優點而在各方面得到廣泛使用，從而帶動鋼構企業迅速發展。如何提高企業生產效率、減少勞力和機械損耗已成為現代鋼構企業追尋的目標。

Job-Shop調度是一種復雜的組合優化問題和典型的NP難題[2]。文獻[3-4]等都提出過關于柔性Job-Shop調度問題的求解方法。本文結合鋼結構的實際生產特點與約束條件，在生產計劃調度系統中建立了多目標生產數學模型，用基于蟻群遺傳混合算法進行求解，并通過方案對比得出了該生產調度系統的高效性、可執行性。

1 系統功能設計

對鋼構企業而言，如何面向多品種小批量的大量訂貨合同而組織生產是生產管理系統面臨的最大困難。因為生產計劃指導著關鍵生產環節的進行，它必須考慮到生產過程中的實際因素，如不同鋼種、規格和交貨期需求，多班組工序分配等。

生產調度是將生產基于訂單合同的生產順序計劃解析成為設備、原料等生產資源的分配依據，以客戶需求為目標，結合企業產能和工藝流程約束，對企業的生產資源進行調度分配，以節約生產時間、提高企業利潤為目標，指導生產活動有序進行[5]。生產計劃與調度在生產系統中的位置關系及信息流動如圖1所示。

2 關鍵算法

鋼構企業的工序多班組選擇調度問題屬于柔性作業車間調度問題。針對該問題，本文提出了通過蟻群遺傳混合算法來實現生產調度的優化選擇，最終使企業生產系統相關性能指標最優，如總完工時間、生產能力與負荷均衡。

2.1 問題描述與建模

工序多班組選擇調度問題可描述為N個工件在M個班組上加工，每個工件至少含一道工序，預先給出工件工序的加工順序，每道工序可由至少一個班組加工，且同一道工序在不同班組上加工工時不同，該作業調度的目標是為工件的每道工序確定合適的班組，完成所有工序的先后加工時間，使各班組的生產能力與負荷均衡，使生產系統完成總任務的時間最短。

根據調度模型需對生產過程做如下假設：

1）工序一旦開始就不能中斷；

2）大型公共設備運輸工序的時間考慮在加工時間范圍內；

3）同一種工件的工序間加工優先級不同，不同工件間的工序加工順序優先級相同；

4）工序在班組上的加工時間是預先給定的；

5）同一工件的工序在同一時刻只能在一個班組上加工，同一時刻一個班組只能加工一個工件。

以下是數學模型中參數和變量的說明：N為工件總數；m為班組總數；Ω為總的班組集；i為班組序號，i=1，2，3…m； j，k 為工件序號， j，k=1，2，3…n；TOj為工件j的總工序數；Ojx為工件j的第x道工序；Xijx為工件j的第x道工序在i上加工；tijx為工件j的第x道工序在i上加工時間；Sjx為工件j的第x道工序加工開始時間；Ejx為工件j的第x道工序加工結束時間；Cmax為最大完成時間。

柔性路徑選擇調度模型必須滿足的約束：

1）每一個工件工序的加工具有優先級，則

2）任一確定時刻，班組i不能同時加工2個不同的工件，也不能同時加工2道不同的工序，則：

多目標優化問題數學模型描述：

給定決策向量 X=（x1，x2，…，xz），滿足的約束條件為

其中：g為q維向量函數；h為p維向量函數；設有t個相互沖突的優化目標，可表示為

則 f為 t維向量函數。 求 X*=（x1*，x2*，…，xz*），使f（X*）在滿足式（6）和式（7）條件下的目標達到最優。為便于求解，將所有優化目標表示為最小化函數，即：

因此目標優化問題的統一表達形式為

多目標生產模型的建立：

在滿足上述條件的前提下，可對調度模型中的工件進行調度，從而確定工件的加工設備，及在設備上的開工時間。考慮生產調度中涉及多個目標函數，建立的調度模型：

1）工件最大完工時間最小

2）瓶頸設備負荷最小

3）設備總負荷最小

所以建立多目標調度問題的數學模型可表達為

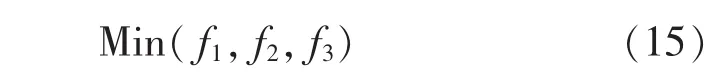
2.2 鋼構件工序在多班組中調度的關鍵算法

圖2 混合算法結構Fig.2 Hybrid algorithm structure

2.3 工序可選班組析取圖模型

采用蟻群優化算法求解FJSP中工藝路線問題，首先將該問題表示成易求解的解構造圖模型，即建立工件各工序可選加工班組析取圖模型，然后將其進一步描述為有向圖G=（V，C∪D）（V為所有節點的集合，C為有向圖G中所有有向弧的集合，D為有向圖G屮所有析取邊的集合）。假設工件數、工序數及在各班組上的加工時間已知，則析取圖模型和有向圖分別如表1和圖3所示。

表1 析取圖模型Tab.1 Disjunctive graph model

圖3 析取圖模型Fig.3 Model of disjunctive

2.4 基于蟻群算法班組分配規則

由析取圖G=（V，C∪D）可設計螞蟻的解構造圖G=（V，C∪D，τ），τ為信息素分布， 代表弧對解質量的影響。根據圖3中析取圖模型，可做出工件J1的解構造圖，如圖4所示。為了便于螞蟻游歷，解構造圖中還標注出了局部啟發式信息，啟發式信息將在后續中介紹。

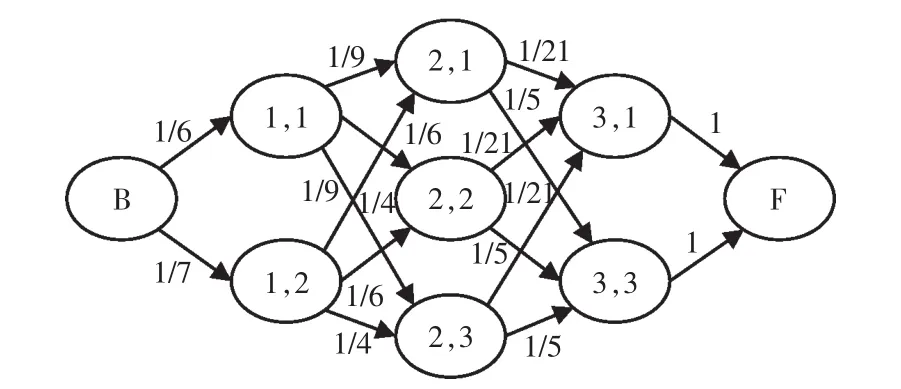
圖4 工件J1的解構造Fig.4 Construction of J1piece

為了能夠提高算法解的質量和縮短搜索時間，本文將采取最短加工時長班組優先被選中策略。并在班組選擇過程中將每個班組已負載的加工時間進行累計，來使班組工作負荷達到平衡。設每個班組已負載的加工時間累計為CMsum，則班組的分配步驟為

1）設置班組負荷矩陣CMsum為1×3的矩陣。每一列分別為M1，M2，M3的總負荷。將該矩陣初始化為［0，0，0］。

2）首先選擇工件J1的工序O11，可選班組為M1，M2。選擇最短加工時長班組M1，則班組負荷矩陣變為 CMsum=［2，0，0］。

3）再選 J1的工序 O12，可選班組為 M1，M2，M3。選擇最短加工時長班組M1，則班組負荷矩陣變為CMsum=［5，0，0］。

4）再選 J1的工序 O13，可選班組為 M1，M3。 選擇最短加工時長班組M3，則班組負荷矩陣變為CMsum=［5，0，5］。

5）以此類推，再分別選擇工件J2的工序O21、O22、O23，則對應的班組負荷矩陣分別為［8，0，5］［8，0，8］［8，3，8］。

2.5 蟻群算法啟發式信息設計

局部啟發式信息η的作用是指引螞蟻選擇加工時間最短的班組，從而有利于總負荷和調度方法的最優化，同時還指引螞蟻選擇已承載負荷少的班組，來使班組間負荷均勻分配。根據分配規則，確定路徑啟發式信息：ηij=1/（CM（1+CMsum）），CM為選擇 M班組的負載，CMsum為選擇M班組時累計負載。啟發式信息數值可見圖4的解構造圖。工件工序間轉移規則為

其它情況 Pijm（t）=0。

式中：Pijm（t）為 t時刻螞蟻 m 選擇（i， j）路徑的概率；τij（t）為 t時刻選擇（i， j）路徑的信息素數量；a 為螞蟻游歷下一道工序時的班組集。

3 軟件實現

工序多設備選擇調度屬于柔性作業調度，本文采用封閉式蟻群-遺傳混合算法進行求解。首先采用蟻群算法解決工序班組選擇問題，從而確定待加工工件相關工序的優選班組；然后采用遺傳算法求解基本班組調度問題。其工作流程如圖5、圖6所示。相關參數設置：蟻群算法參數借鑒文獻[6]，迭代數Nc=50、螞蟻數m=8、啟發式因子重要程度參數β=5、信息重要程度參數α=1、信息素揮發率ρ=0.3、信息素增強度系數Q=6，遺傳算法參數借鑒文獻[7]，群體大小50、迭代次數maxGen=40、交叉因子pxover=0.85、選擇算子psel=0.1、變異因子pmutation=0.2。

圖5 遺傳算法流程圖Fig.5 Flow chart of genetic algorithm

圖6 蟻群遺傳算法流程圖Fig.6 Flow chart of ant colony genetic algorithm

4 應用與結果分析

以表1中工件工序的可加工分布情況為例，將本文提出的蟻群遺傳混合優化算法應用于其中，通過編程進行實現。經過優化排序得到工件工序最終加工順序，如表2所示。

表2 工件工序加工順序Tab.2 Order of workpiece machining processes

由加工順序生成的甘特圖如圖7所示。

圖7 排產甘特圖Fig.7 Scheduling Gantt

若不使用該方法進行排產，得到工件工序加工順序如表3所示。

表3 工件工序加工順序Tab.3 Order of workpiece machining processes

生成相應的排產甘特圖如圖8所示。

由圖7和圖8的排產甘特圖對比可知，通過蟻群遺傳混合算法優化得到的排產方案要優于不用此方法的排產方案，可提前3個工作日完成工作任務。

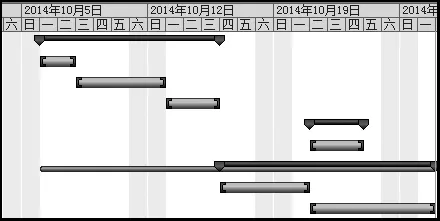
圖8 排產甘特圖Fig.8 Scheduling Gantt

5 結語

本論文討論的是工序多設備選擇調度的柔性作業問題，建立柔性作業的工序約束和生產調度模型。在算法中著重討論了班組分配問題，并提出通過蟻群遺傳混合算法來解決該問題。應用結果表明該方法是有效的。下一步將優化算法中的相關參數，以進一步提高分配效率。

[1]黃肖玲，柴天佑.復雜生產過程計劃調度級聯模型在選礦MES中的應用研究[J].自動化學報，2011，37（9）：1130-1139.

[2]Kacem I，Hammadi S，Borne S，et al.Pareto-optimality approach for flexible Job-Shop scheduling problems：hybridization of evolutionary algorithms and fuzzy logic[J].M Athematics and Computers in Simulation，2002，60（3-5）：245-276.

[3]張維存，鄭丕諤，吳曉丹.基于蟻群粒子群算法求解多目標柔性調度問題[J].計算機應用，2007，27（4）：936-938，941.

[4]夏蔚軍，吳智銘.基于混合微粒群優化的多目標柔性Job-Shop調度[J].控制與決策，2005，20（2）：137-141.

[5]鄧宇巍.熱軋帶鋼生產調度模型與算法研究[D].上海：上海交通大學，2007.

[6]CARLIER J，PINSON E.Adjustment heads and tails for the job shop scheduling problem[J].European Journal of Operational Research，1994，78（3）：146-161.