WGS-84坐標系下空基多平臺異質傳感器MLR配準*

?

WGS-84坐標系下空基多平臺異質傳感器MLR配準*

吳衛華，江晶

(空軍預警學院，湖北 武漢430019)

摘要：多平臺多傳感器良好協同的重要前提之一是其系統誤差的配準，由于空中平臺的運動和傳感器類型的異質性使得配準問題更為復雜。首先構建了WGS-84坐標系下有偏觀測模型，然后將最大似然配準(maximum likelihood registration, MLR)算法擴展到空基多運動平臺異質傳感器的配準。運用復合函數求導鏈式法則，推導出應用MLR算法時至為關鍵的傳感器觀測量對目標狀態的雅克比矩陣。理論和仿真結果表明該方法可實現異質傳感器配準，配準誤差逼近其Cramer-Rao界。

關鍵詞：異質傳感器配準；最大似然配準；WGS-84；多運動平臺

0引言

將已有的各自獨立的傳感器組網，可有效提高系統的整體性能：如穩健性、覆蓋范圍、探測跟蹤精度等，相比研發全新的裝備，無疑是一種更為經濟高效的方式[1]。然而，受傳感器系統偏差的影響，首先需要解決傳感器配準問題，否則，不但可能起不到提升性能的作用，甚至將造成性能的惡化，如對同一個目標可能在統一態勢圖上產生多條虛假航跡的“鬼影”(ghost)[2]。

為實現傳感器的配準，主要有2類算法：一是為了達到實時性而提出的在線配準遞歸算法[3]；另一類是離線模式下的批處理算法。后者主要應用于傳感器偏差在短時間變化緩慢的情況，其可進一步細分為最小二乘配準(least square registration, LSR)[4-5]和最大似然配準(maximum likelihood registration, MLR)[6-10]算法。LSR一般適用于同類傳感器之間的兩兩相對配準，而MLR可用于任意數目的異質傳感器之間的絕對配準，同時可對未知目標進行跟蹤。

最初，MLR是基于二維區域性平面的球面投影(stereographic projection)[8-9]，隨后，為在大范圍監視區域精確的配準，文獻[10]利用了從本地傳感器量測到WGS-84坐標系的高精度大地坐標變換，提出了基于WGS-84坐標系的最大似然配準(WGS-84-MLR)算法(文獻[10]的ECEF即為本文的WGS-84坐標系)。不過，上述文獻主要是針對地面固定多站，文獻[11]應用該算法對空基多運動平臺進行了研究，但沒有考慮姿態信息。為更貼近于WGS-84坐標系下的空基多運動平臺，本文考慮平臺不斷變化的位置和姿態，研究了空基多平臺多異質傳感器的最大似然配準問題。

1WGS-84坐標系下有偏觀測模型

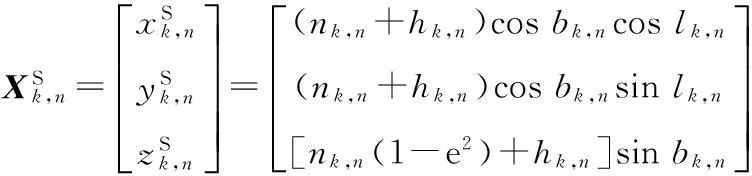
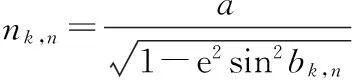
設目標在WGS-84坐標系下的位置為Xk=(xk,yk,zk)T，則根據WGS-84坐標系到載機NED坐標系[12](該坐標系原點在載機質心處，地理北、東分別為x，y軸，z軸與x，y軸成右手系朝下)的坐標變換公式，可得目標在平臺n的NED坐標系下的坐標為

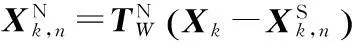
(1)

式中：

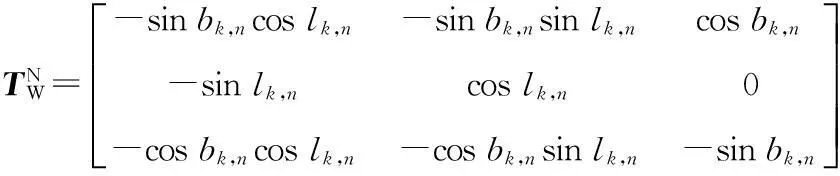
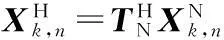
(2)

式中：

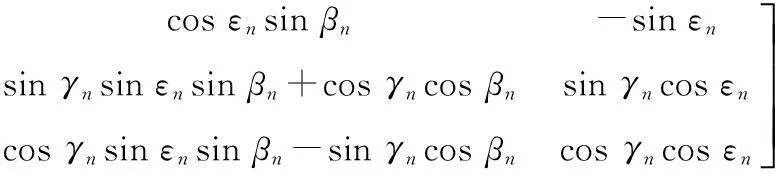
式中，為使式子簡明，省略了表示時間索引的下標k。

當平臺配置的傳感器為有源類型時，觀測集為斜距rk,n,方位ak,n(相對于機頭，向右為正)和俯仰角ek,n：

zk,n=(rk,n,ak,n，ek,n)T.

當平臺配置的傳感器為無源傳感器時，此時無斜距信息，觀測集為方位和俯仰角：

zk,n=(ak,n，ek,n)T，

式中：

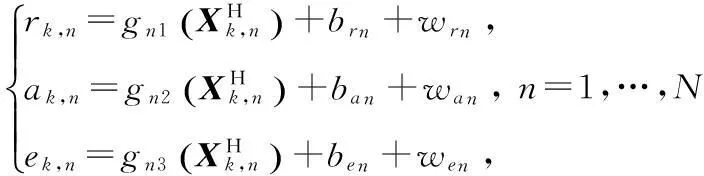
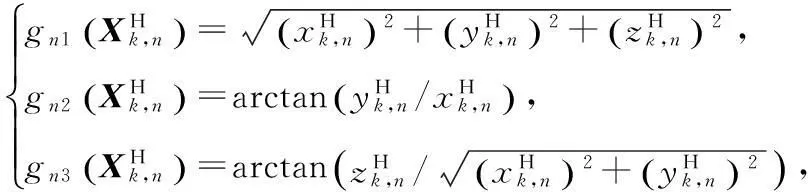
將上式寫成矢量緊湊形式有

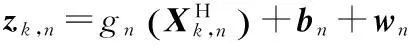
(3)

將式(1)和式(2)代入式(3)，從而可得觀測與目標狀態的非線性函數關系為

(4)

式中：待估計的狀態為Xk∈p；是已知的非線性矢量量測函數。假定配準參數矢量bn為時不變確定量，并與Xk獨立；wk,n為零均值白高斯噪聲，協方差矩陣為∑zn；并且噪聲序列wk,n在平臺間相互獨立，且有zk,n,hn,bn,wk,n∈qn。

2最大似然配準(MLR)算法

將N個傳感器的觀測矢量合并成一列，則有

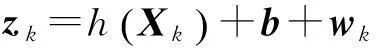
(5)

式中：

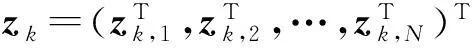
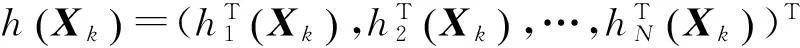
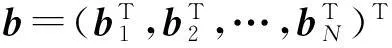
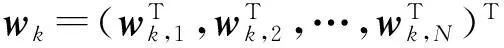
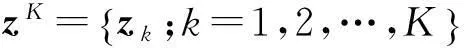
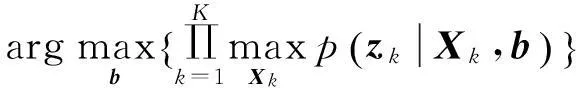
(6)

2.1目標狀態估計

根據式(5)，可得目標狀態與觀測量有如下非線性關系：

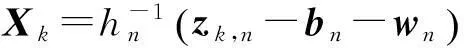
式中：wk,n反映了上述映射是隨機的。

那么，可將傳感器n的觀測量按下式(7)投影到目標狀態空間

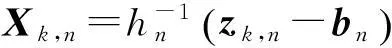
(7)

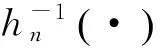
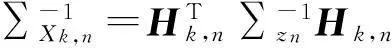
(8)

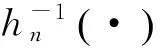
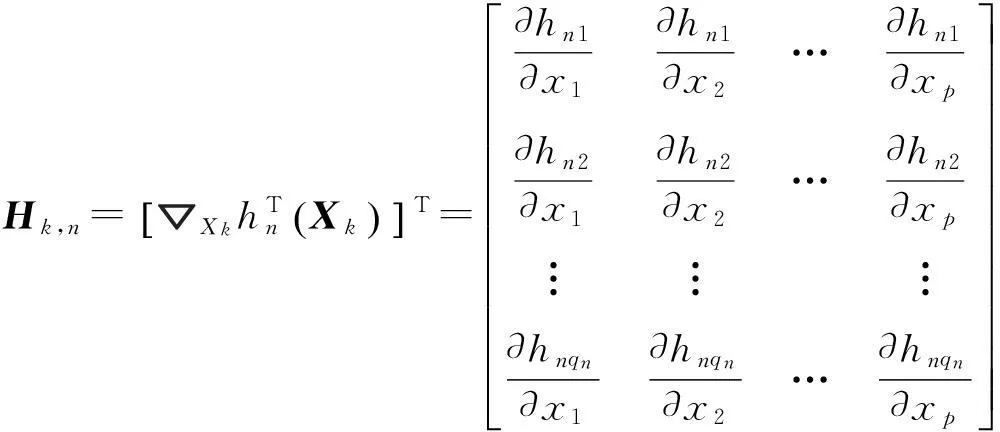
(9)

k時刻目標狀態的最大似然估計(maximum likelihood estimate, MLE)[9]為

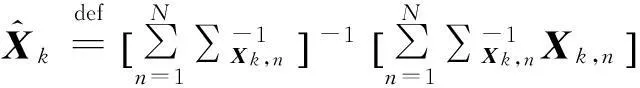
(10)

由式(7)可知，該估計依賴于未知的偏差矢量bn，它將由下節的算法進行估計。

2.2傳感器偏差估計

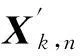
式中：雅克比矩陣Hk,n(qn×p維)由式(9)定義，上標-L表示左逆。該式用于迭代計算傳感器偏差b。

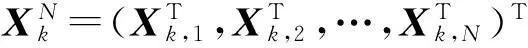
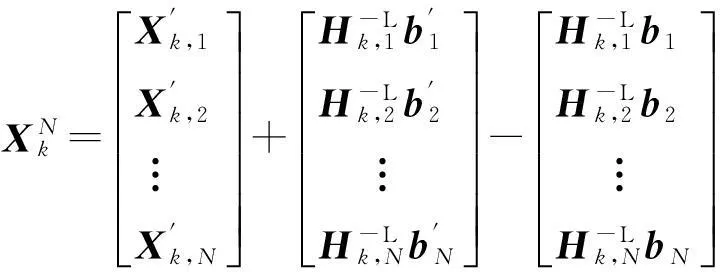
或者寫成更緊湊的形式：

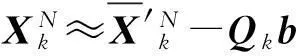
(12)

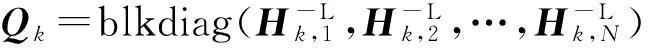
(13)

(14)

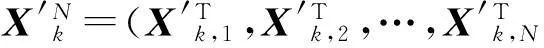
b的MLE為[9]

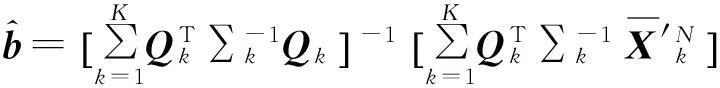
(15)

式中：

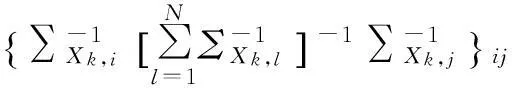
(16)

blkdiag(·)為Matlab函數，實現將輸入子矩陣構造成對角塊矩陣功能。式中的{·}ij表示尺寸為p×p的子矩陣所在位置為(ij)，其中，i,j=1,2,…，N。

2.3MLR算法執行

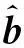
2.4Cramer-Rao界

假設b是需要估計的，而Xk是已知的，可以得到MLR算法較保守(低于實際值)的CRLB[9]

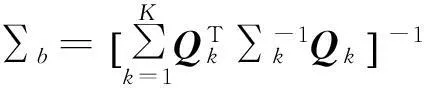
(17)

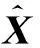
3MLR算法應用于WGS-84坐標系空基多運動平臺異質傳感器

由MLR算法過程可知，該算法至為關鍵的式子為Hk,n。為了將該算法應用于WGS-84坐標系下的空基多運動平臺，需要求出觀測量對目標狀態的雅克比矩陣。

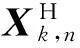
當傳感器為有源類型時：

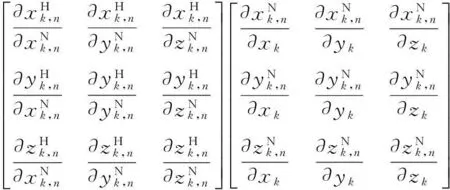
進一步化簡可得

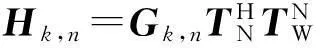
(18)

式中：

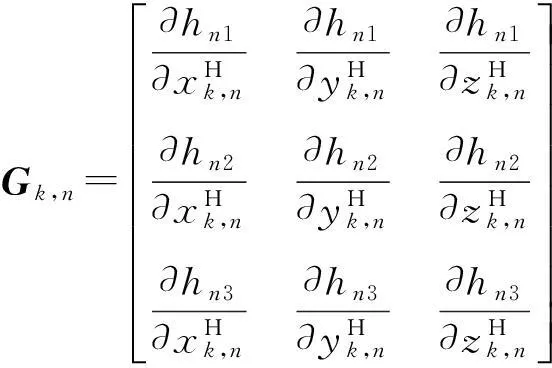
(19)

當傳感器為無源類型時：

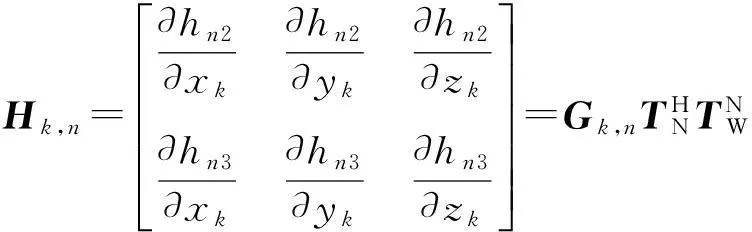
(20)

此時，

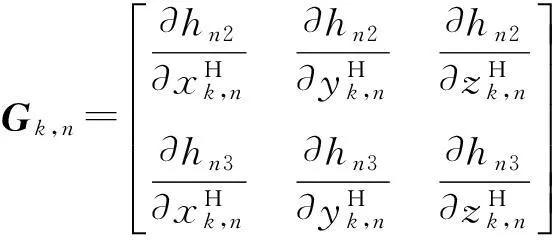
(21)

式中：

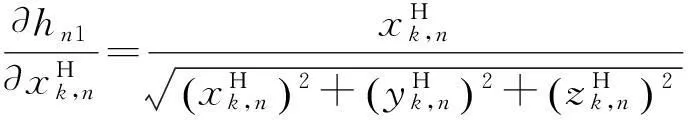
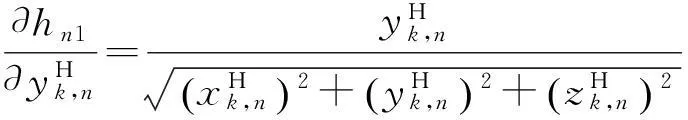
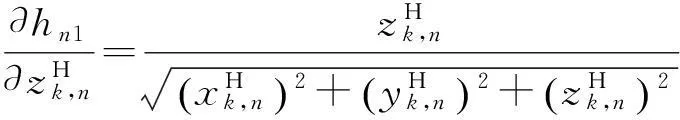
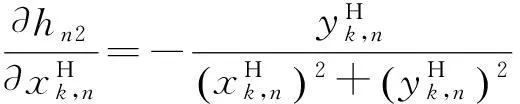
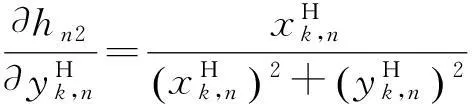
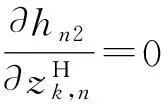
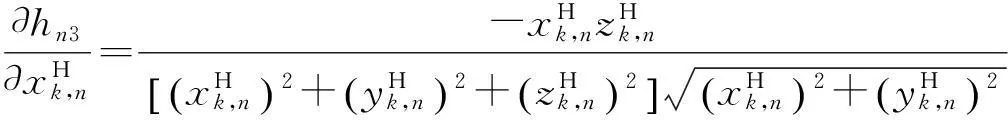
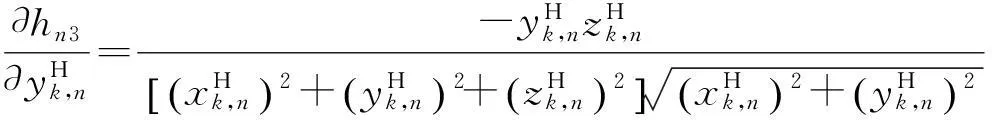
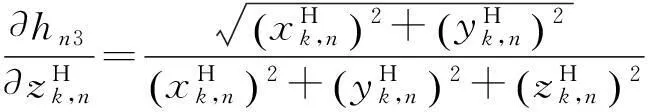
得到Hk,n后，即可根據MLR算法對空基多平臺的傳感器偏差進行配準。

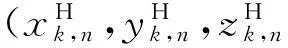
4仿真分析

考慮2個(N=2)機載平臺對同一未知運動目標的配準，假設兩平臺均做勻速直線運動，平臺1的初始經緯高為119° E，24°N，8 000 m，初始速度為(100，-200，0)Tm/s，平臺2的初始經緯高為119° E，26°N，8 000 m，初始速度為(100，200，0)Tm/s。目標的初始經緯高為121° E，25°N，3 000 m，按如下方程運動：

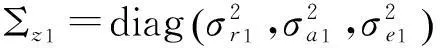
圖1給出了算法的一次運行仿真結果(K=160)。從圖1可知，從初始值b=05×1開始迭代，僅需3次迭代，各項偏差均可達到收斂。圖2可看出配準補償后的斜距、方位和俯仰角與真實值非常接近。

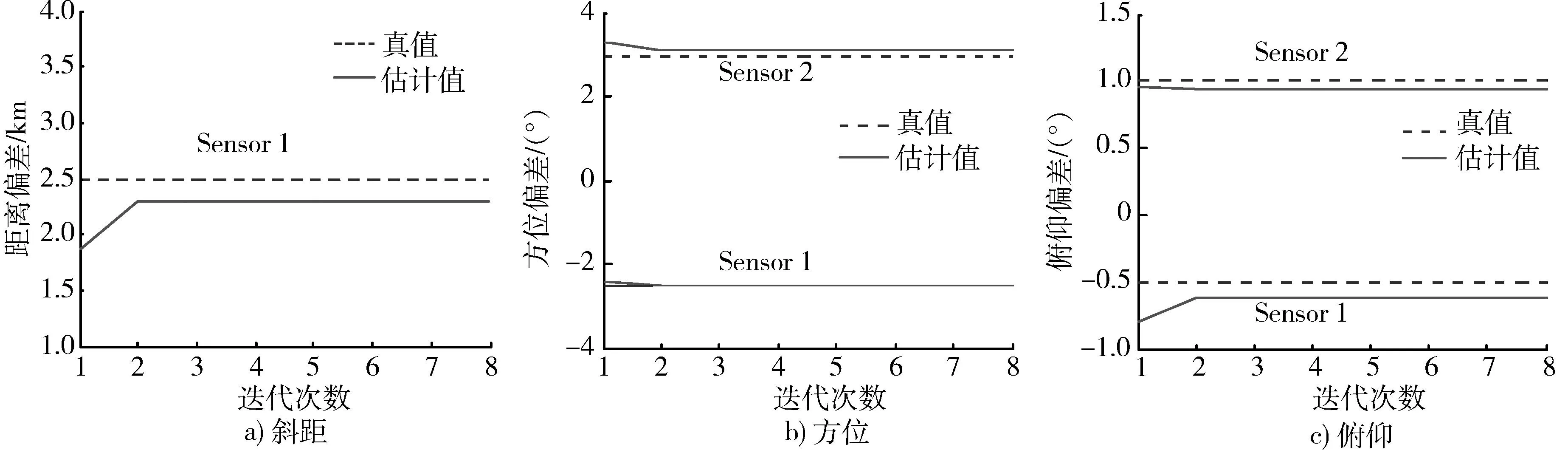
圖1　不同迭代次數下各平臺的傳感器偏差估計結果Fig.1　Each sensor’s biases estimation during iteration process

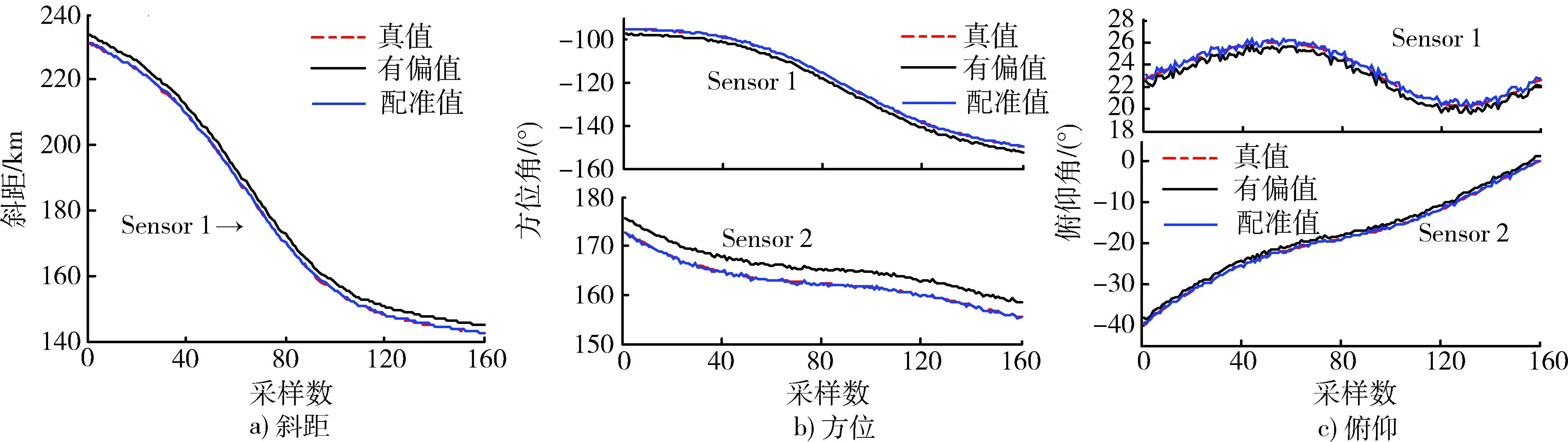
圖2　平臺1和平臺2的傳感器配準前后觀測與其真實值比較Fig.2　Unregistered and registered measurements (sensor 1 and 2) versus true values

圖3　各平臺傳感器偏差估計誤差均值Fig.3　Mean of sensor bias estimation errors

圖4　各平臺偏差估計誤差標準差與CRLB比較Fig.4　Comparison of standard deviation of sensor bias estimation error and CRLB

5結束語

本文給出了應用于WGS-84坐標系下空基多平臺異質傳感器的MLR配準算法。仿真結果表明，該算法對空基異質傳感器偏差是漸進無偏的有效估計量。下一步將對WGS-84坐標系下空基多運動平臺的無源傳感器配準問題展開研究，以及實現空基平臺姿態偏差的配準。

參考文獻：

[1]Dela Cruz E J, Ali T Alouani, Theodore R Rice,et al. Sensor Registration in Multisensor systems [C]∥Proceeding of the SPIE Symposium on Aerospace Sensing(Conference on Signal and Data Processing of Small Targets), Orlando, SPIE, 1992, 382-393.

[2]Gregory A Watson, Theodore R Rice. Sensor Alignment and compensation for Composite tracking [C]∥ Signal and Data Processing of Small Targets, Orlando, SPIE, 2002：354-367.

[3]連峰, 韓崇昭, 彭一峰, 等. 基于廣義似然比的自適應在線配準算法 [J]. 控制與決策, 2009,24(1) : 23-28.

LIAN Feng,HAN Chong-zhao,PENG Yi-feng, et al. Adaptive on-Line Registration Algorithm based on GLR [J]. Control and Decision, 2009,24(1) : 23-28.

[4]ZHOU Yi-feng; LEUNG H, BLANCHETTE M. Sensor Alignment with Earth-Centered Earth-Fixed (ECEF) Coordinate System [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999,35(2) : 410-418.

[5]Stefano Fortunati, Alfonso Farina, Fulvio Gini, et al. Least Squares Estimation and Cramer-Rao Type Lower Bounds for Relative Sensor Registration Process [J]. IEEE Transactions on Signal Processing, 2011,59(3) : 1075-1087.

[6]ZHOU Yi-feng; LEUNG H， YIP P C. An Exact Maximum Likelihood Registration Algorithm for Data Fusion [J]. IEEE Transactions on Signal Processing, 1997,45(6) : 1560-1573.

[7]Hwa-Tung Ong. Sensor Registration Using Airlanes: Maximum Likelihood Solution [C]∥ Signal and Data Processing of Small Targets 2003, Orlando: SPIE, 2003：390-401.

[8]MCMICHAEL D, OKELLO N. Maximum Likelihood Registration of Dissimilar Sensors [C]∥ Proceedings of the First Australian Data Fusion Symposium, Adelaide, Australia,1996：31-34.

[9]OKELLO N, RISTIC B. Maximum Likelihood Registration for Multiple Dissimilar Sensors [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003,39(3) : 1074-1083.

[10]RISTIC B, OKELLO N. Sensor Registration in ECEF Coordinates Using the MLR Algorithm [C]∥ Proceedings of the 6th International Conference on Information Fusion (Fusion 2003), Cairns, Australia: ISIF, 2003：135-142.

[11]JIANG Jing, YUAN Jun-quan, MA Xiao-yan, et al. Divided Segment ML Registration for Multiple Moving Platforms Multiple Dissimilar Sensors [C]∥ Radar, 2006. CIE '06. International Conference on, 2006：1-5.

[12]江晶. 多運動平臺多傳感器信息融合技術應用研究[D]. 湖北武漢：武漢大學，2006.

JIANG Jing. Study on Multiple Moving Platforms Multiple Sensors Information Fusion Application [D]. Wuhan: Wuhan University, 2006.

MLR Registration for Dissimilar Sensors of Multiple Airborne Platforms in WGS-84

WU Wei-hua, JIANG Jing

(Air Force Early Warning Academy, Hubei Wuhan 430019, China)

Abstract:It is a precondition of coordinated operation for multi-platforms and multi-sensors to register these sensors, the registration problem will become more complex owing to airborne platforms’ motion and dissimilar sensors. Firstly, the biased measurement model based on WGS-84 (world geodetic system-84) coordinate system is constructed, and then the maximum likelihood registration (MLR) algorithm is extended to active sensor registration for multiple moving airborne platforms in WGS-84. By using the chain derivative rule of composite function, when MLR is applied, the key Jacobi matrix of sensor measurements to target state is derived. Theory analysis and simulation results show that the method can realize sensor registration, and the registration errors can approach the Cramer-Rao low bound.

Key words:dissimilar sensor registration; maximum likelihood registration (MLR); world geodetic system-84 (WGS-84); multiple airborne platforms

中圖分類號：TN959.7; TP301.6

文獻標志碼：A

文章編號：1009-086X(2015)-02-0130-07

doi:10.3969/j.issn.1009-086x.2015.02.021

通信地址：430019湖北省武漢市江岸區黃浦大街288號931信箱E-mail： weihuawu1987@163.com

作者簡介：吳衛華(1987-)，男, 湖南邵陽人。博士生, 研究方向為多源信息融合。

基金項目：國家自然科學基金項目(61102168)

* 收稿日期：2014-03-21；
修回日期：2014-06-28