冉紹爾-湯森效應及其電流電壓關系

曹鈞植，楊新菊，姚紅英

(復旦大學 物理系，上海 200433)

冉紹爾-湯森效應及其電流電壓關系

曹鈞植，楊新菊，姚紅英

(復旦大學 物理系，上海 200433)

摘要：電子流在與氣體閘流管中稀有氣體作用時，出現經典理論無法解釋的冉紹爾-湯森效應，即氣體散射截面和電子速度有關. 研究了此過程中幾何因子、散射概率和總散射截面隨電子速度的變化規律，驗證了冉紹爾-湯森效應. 探究了實驗中出現的陰極電流和加速電壓偏離二分之三關系的現象，利用排除法確定了可能的原因：經典Drude模型無法較好地描述電子和氣體的碰撞.

關鍵詞：冉紹爾-湯森效應；氣體閘流管；二分之三關系；總散射截面

1引言

物理學家冉紹爾和湯森發現在電子和氣體的碰撞中，氣體散射截面和電子速度相關[1]，該現象稱之為冉紹爾-湯森效應. 而在經典理論中將氣體視為小球，則氣體散射截面和電子速度無關，因此冉紹爾-湯森效應需要用量子力學解釋[2-3].

實驗中采用氣體閘流管體系，加熱燈絲產生熱電子并且用電場加速電子，使電子和氣體分子碰撞并且通過收集閘流管中不同極板的電流，分別在常溫下和液氮溫度下進行實驗，得到各極板電流隨加速電壓變化關系，最終計算出閘流管幾何因子f、氣體散射概率Ps和總散射截面Q隨電子速度va的變化，驗證了冉紹爾-湯森效應. 同時通過總電流和加速電壓關系偏離二分之三定律的位置確定氣體電離電壓.

2實驗原理

2.1　冉紹爾-湯森效應

冉紹爾-湯森效應是指氣體散射截面和電子速度相關的現象，對于稀有氣體原子，其關系如圖1所示，氣體的總散射截面與電子速度有關. 可以通過量子力學中的分波帶法，求解電子在原子勢場中波函數從而得到此結果[2].

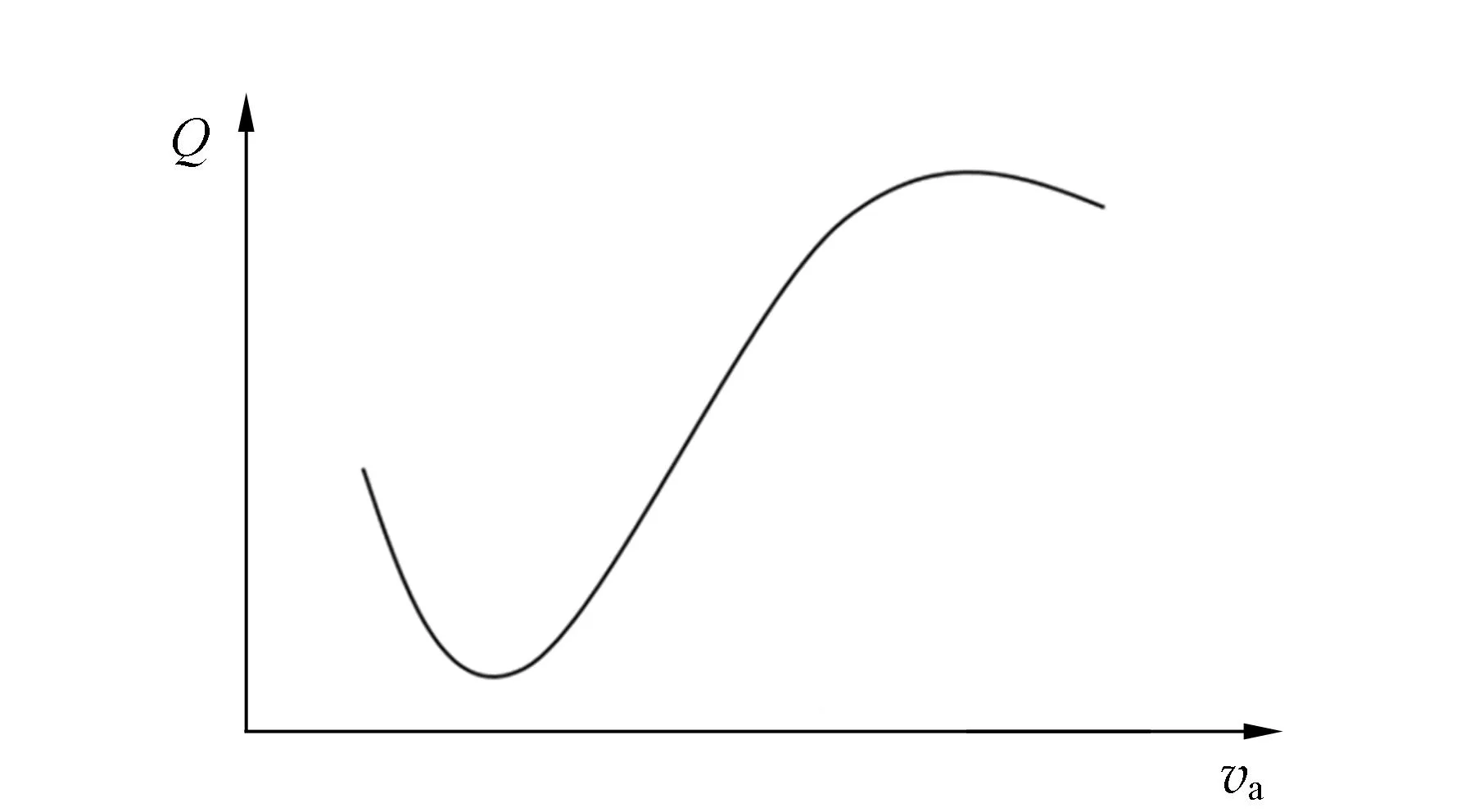
圖1　冉紹爾-湯森效應

2.2　氣體閘流管

ZQI 0.1/1.3型氣體閘流管結構如圖2所示，其中充有稀薄的Kr和Xe混合氣體，使用電壓Ef加熱陰極，溢出熱電子形成陰極電流IK；之后在K和S之間施加加速電壓Ea加速電子，電子經過加速后到達等勢區與氣體分子碰撞，未經散射的電子到達P極板，未通過S極小孔的電子形成電流IS1，通過S的電子形成電流I0，一部分未到達P，形成IS2，其他的電子打在P極板上形成電流IP，為了補償接觸電勢差和空間電荷分布造成的電勢差，實驗中在S和P之間施加額外的電壓Ec進行補償. 實驗中測量出屏蔽極電流IS和收集極電流IP，各部分電流之間有如下關系：

IK=IS1+IS2+IP，

I0=IS2+IP，

IS=IS1+IS2，

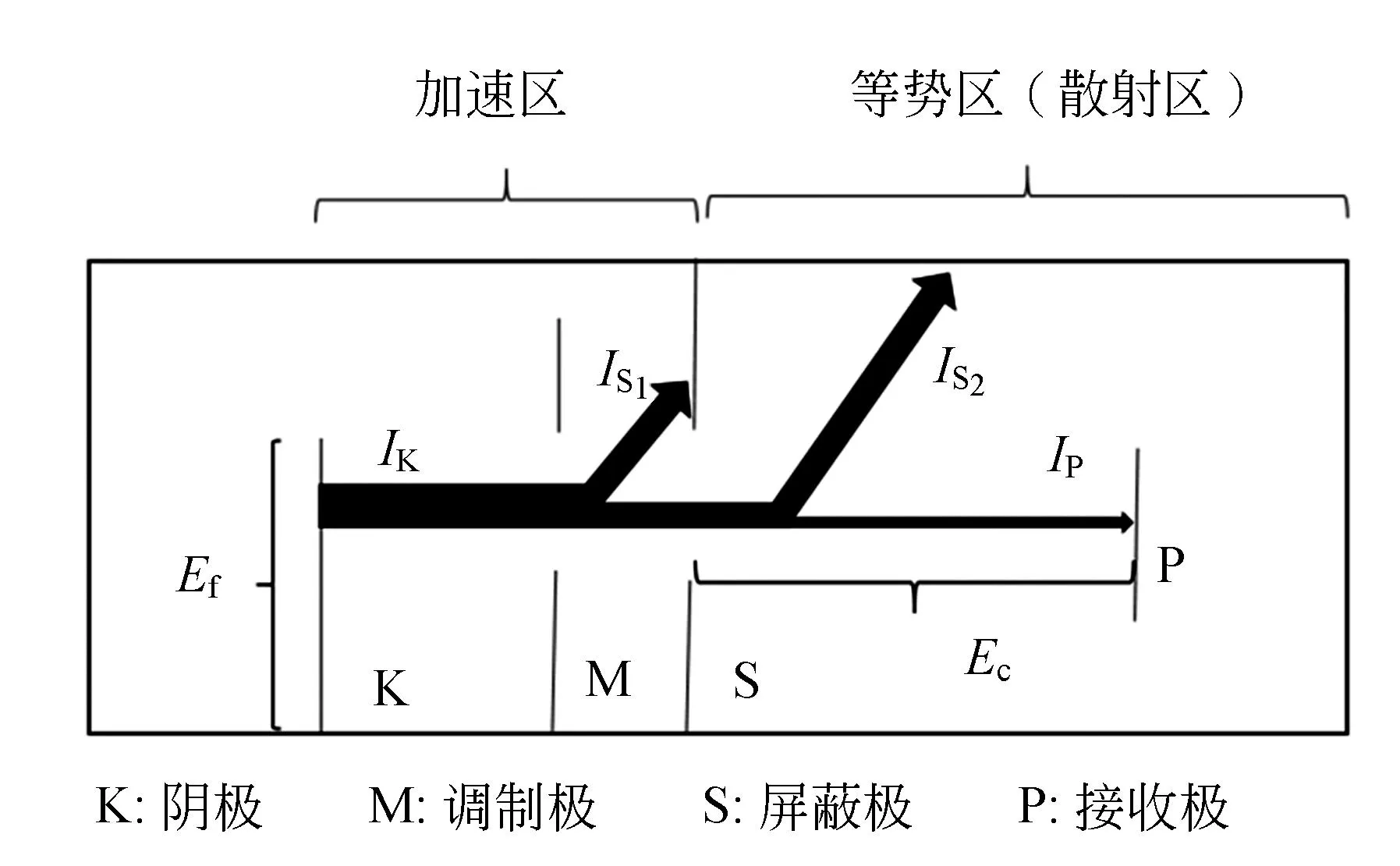
圖2　氣體閘流管的結構

其中只有IS和IP可以測量到.

2.3　計算幾何因子f、散射概率Ps及總散射截面Q

定義幾何因子f，刻畫I0和IS1的關系：

f=I0/IS1,

(1)

幾何因子與氣體閘流管結構、空間電荷分布及電子速度均有關系. 定義散射概率Ps刻畫電子在等勢區內的散射

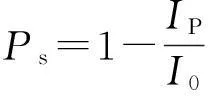
(2)

結合式(1)和(2)得到

(3)

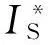
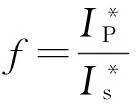
在加速電壓Ea和燈絲陰極溫度相同的條件下，低溫下的幾何因子和常溫下的幾何因子應相同. 實驗中f?1，因此IS≈IS1，最終可以得到

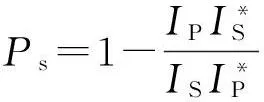
(4)

假設L為出射孔S和極板P的距離(實驗中L=6.5 mm)，那么

Ps=1-e-n σL,

(5)

其中,n是氣體薄層的面密度，σ是單個氣體原子的散射截面，定義Q=nσ為總的散射截面[4]，因此有

(6)

2.4　二分之三關系及電離電壓的測量

理想真空二極管工作在空間電荷區時，陽極電流和陽極電壓的3/2次方成正比，即Child-Langmuir定律. 如果把氣體閘流管視為工作在空間電荷區的理想真空二極管，則有

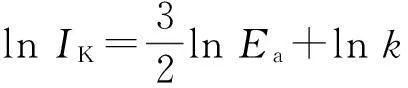
(7)

IK為IS+IP，k為斜率，和電極形狀有關，實驗中保持不變. 實驗中增大電子加速電壓Ea，如果出現電離，那么IK會突然增大，偏離二分之三關系，以此確定氣體原子電離電壓. 實驗中測量的是Xe的電離電壓，公認值為12.13 V.

3實驗內容

實驗線路圖如圖3所示[3].

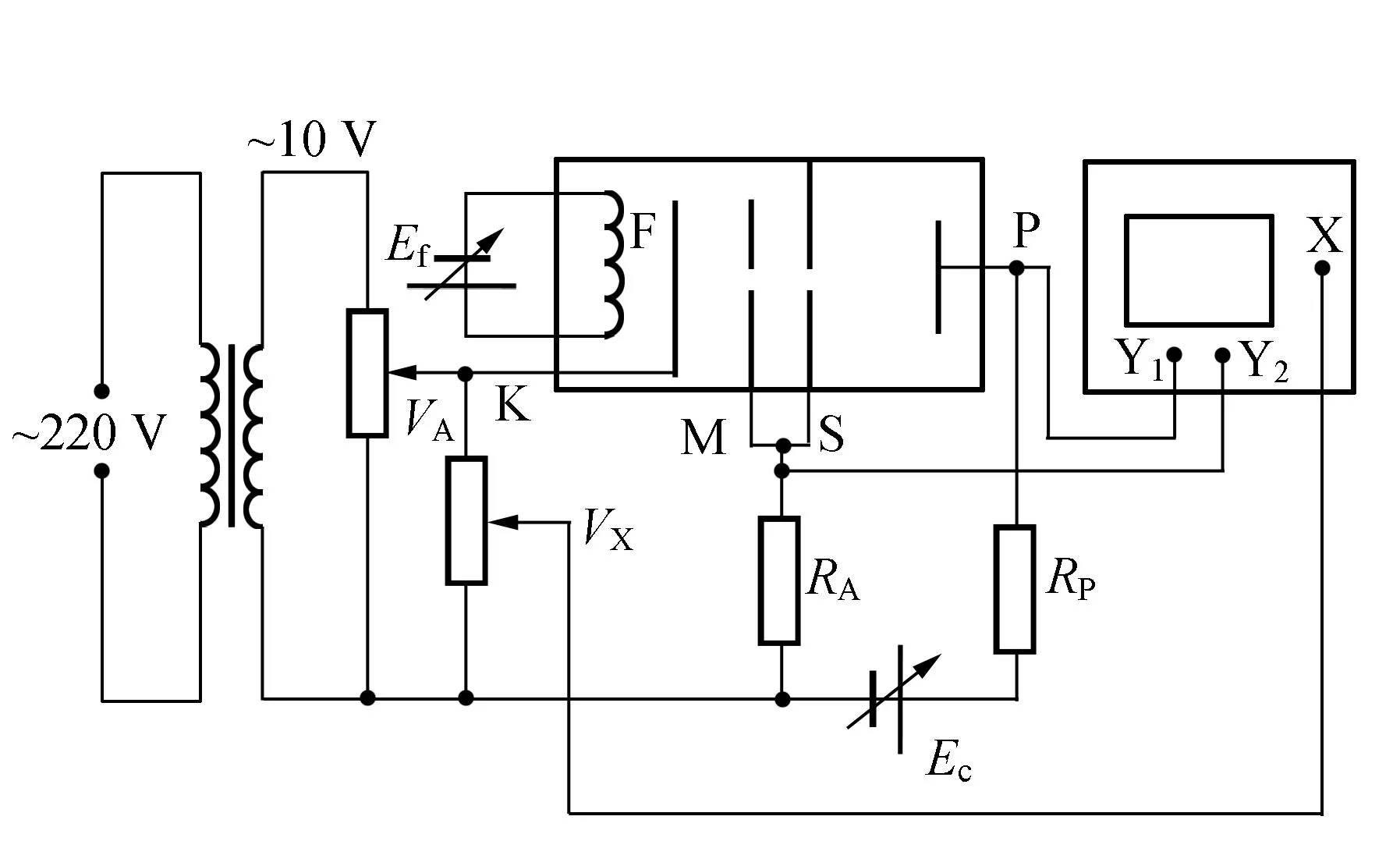
(a)使用交流加速電壓接線圖

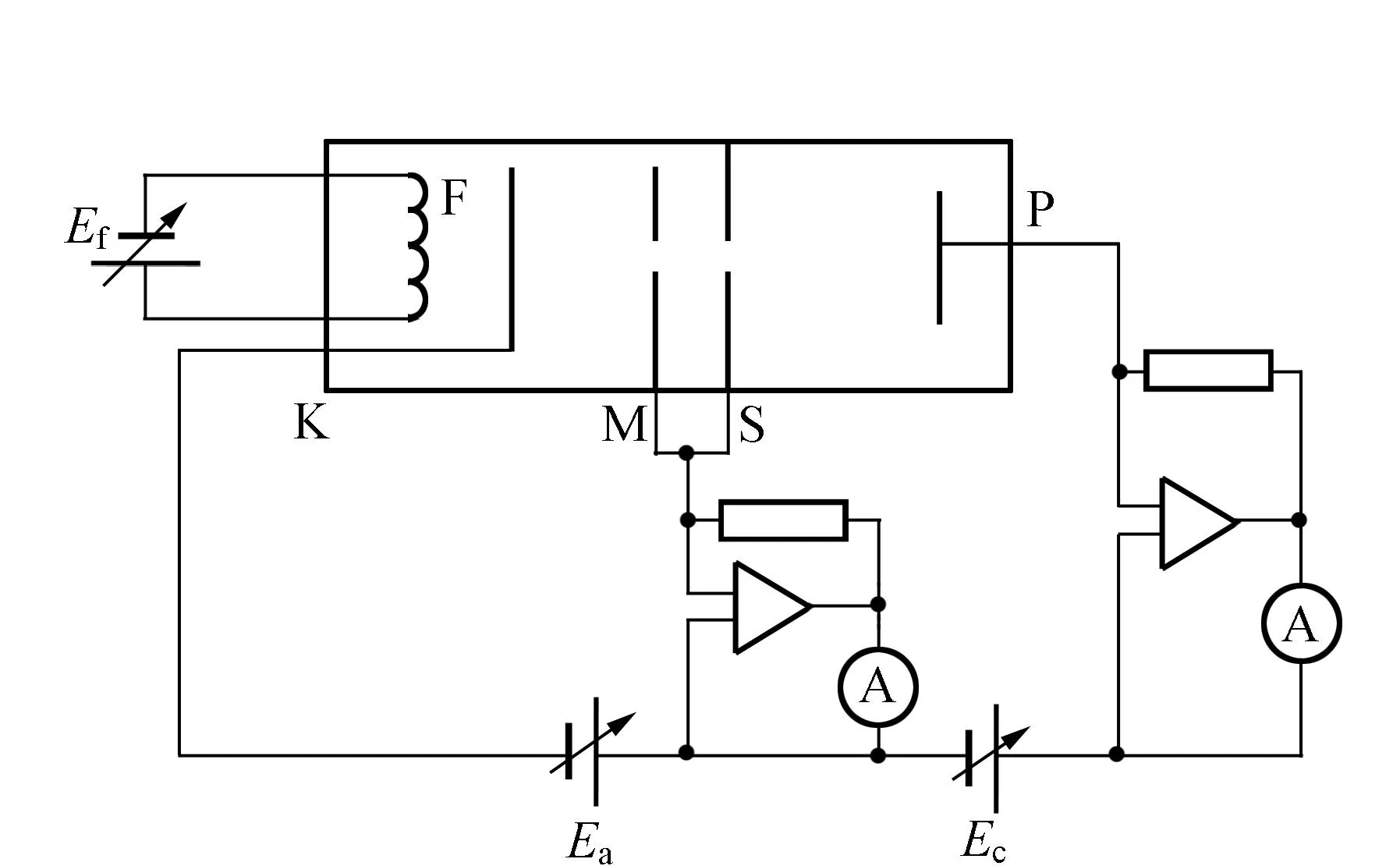
(b)使用直流加速電壓接線圖圖3　直流電路和交流電路接線圖

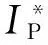
2)直流電路下精確測量：常溫下測量IP和IS與加速電壓關系，調節補償電壓Ec使IS和IP同時出現以確定Ec；低溫下測量IP和IS與加速電壓關系(注意調節Ef保證陰極電流和常溫相同).

3)根據直流電路的結果計算幾何因子f、散射概率Ps和散射截面Q隨加速電壓變化趨勢，驗證冉紹爾-湯森效應.

4)通過陰極電流IK和加速電壓Ea的關系確定Xe原子的電離電壓.

4實驗結果及討論

4.1　屏蔽極電流IS和收集極電流IP隨加速電壓Ea的變化

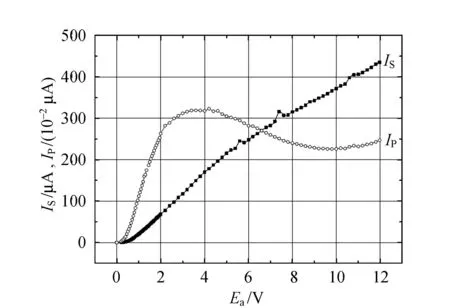
(a)常溫下IP和IS隨Ea變化

(b)低溫下和隨Ea變化圖4　板極電流隨電子速度Ea的變化規律

4.2　幾何因子f、散射概率Ps和散射概率Q隨電子速度va的變化關系

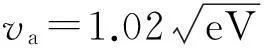
(a) f隨va變化規律

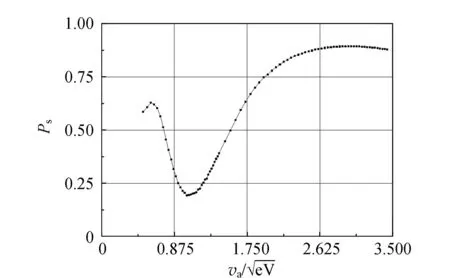
(b) Ps隨va變化規律

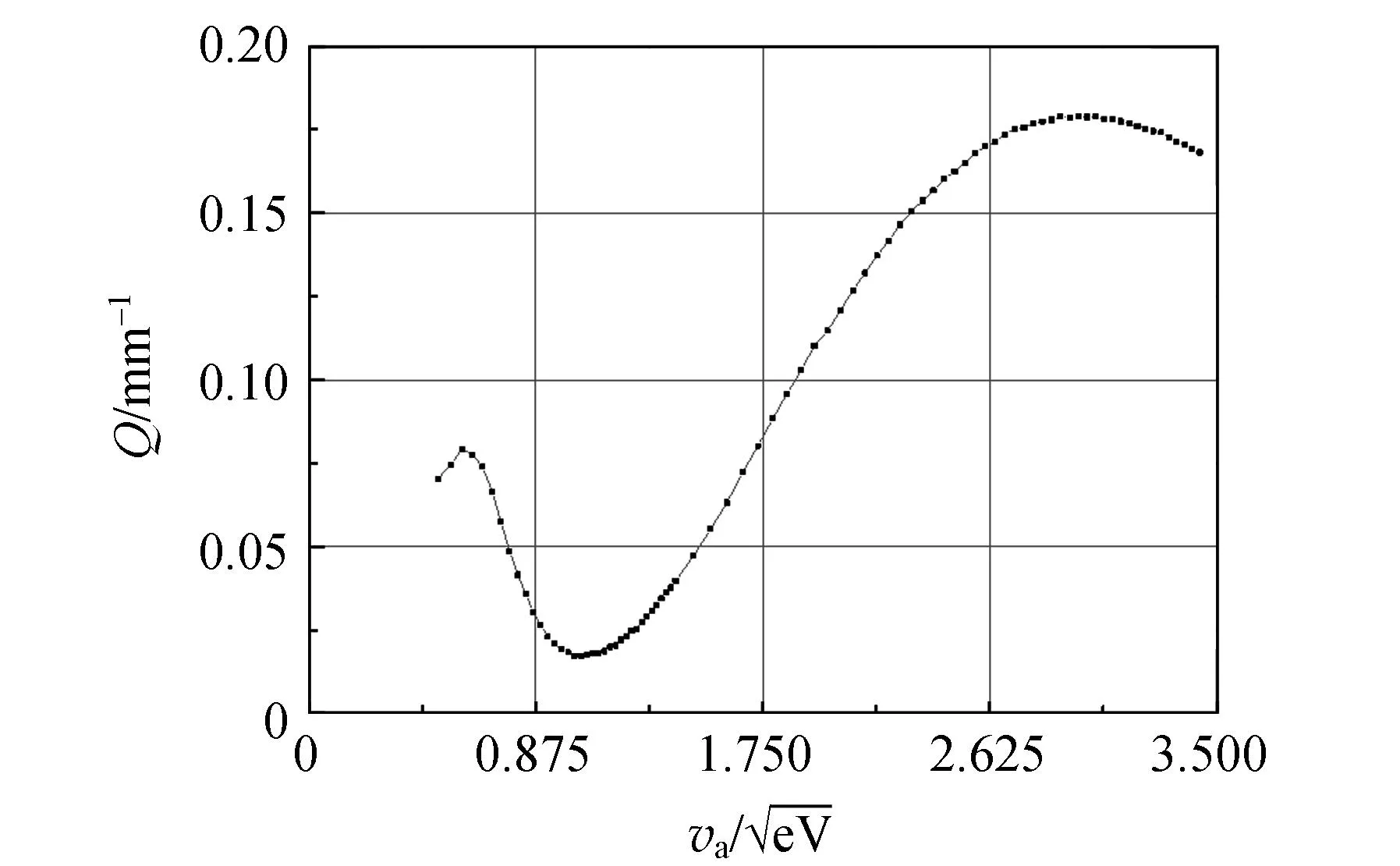
(c) Q隨va變化規律圖5　幾何因子f、散射概率Ps和總散射截面　Q隨電子速度va的變化

4.3　電離電壓測量以及偏離二分之三關系現象的確定

根據IK和Ea的關系[圖6(a)]確定Xe原子電離電壓為13.0 V(標準值12.13 V). 從圖6(a)和圖6(b)中2條直線的斜率可以看出，無論是低溫還是常溫，IK和Ea的關系都偏離二分之三關系，低溫下更接近.

(a)常溫下ln IK和ln Ea的關系(直線部分斜率1.21)

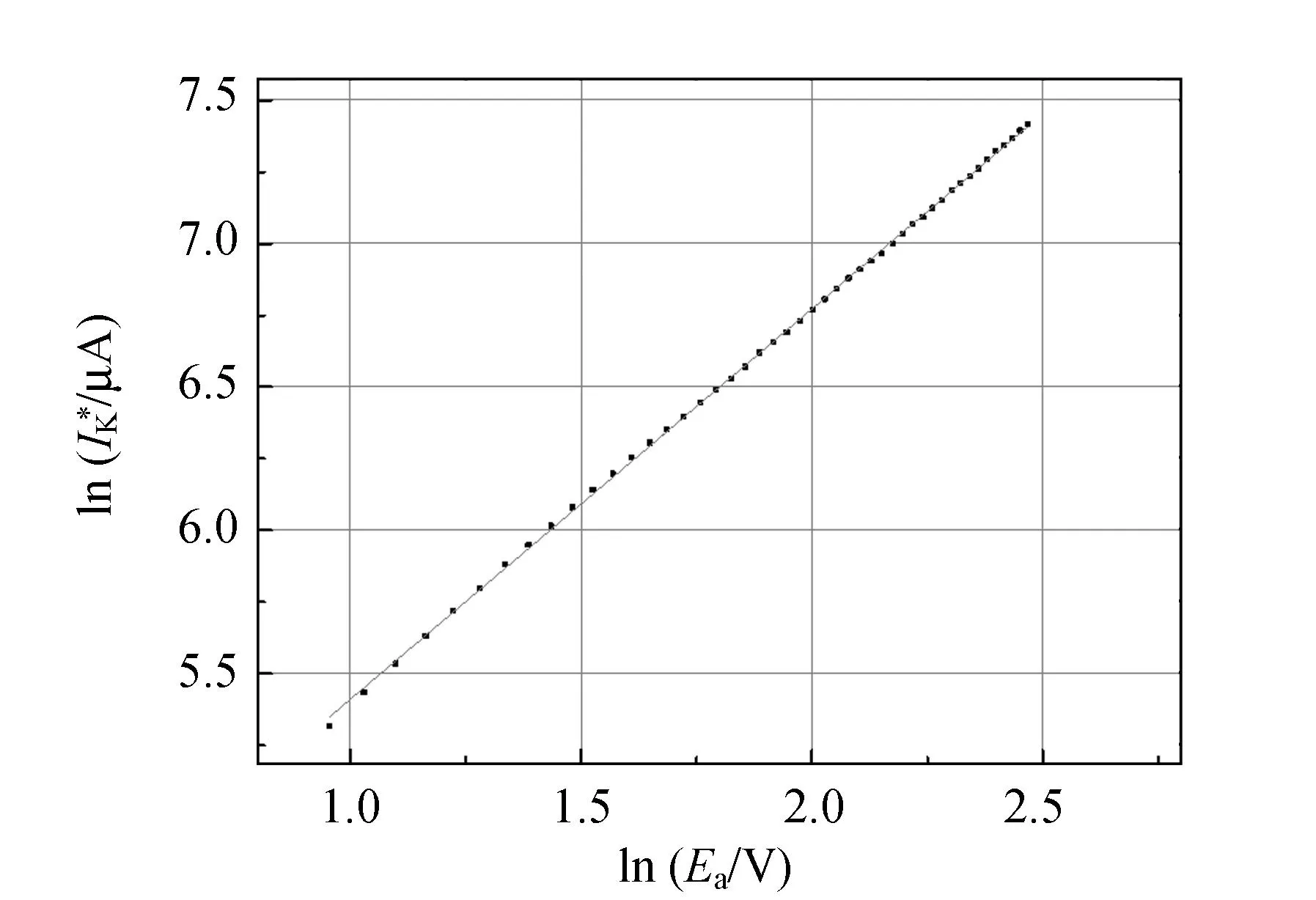
(b) 低溫下和ln Ea的關系(直線部分斜率1.36)圖6　陰極電流ln IK和加速電壓ln Ea的關系

4.4　分析偏離原因

首先考慮二分之三定律成立的條件是否滿足. 二分之三定律要求體系為真空理想二極管，并且工作在空間電荷區. 由于體系為充有稀薄氣體的氣體閘流管，接近真空，參考文獻[1]中也認為可以近似為真空理想二極管，所以暫時假設其成立. 同時，工作在空間電荷區的條件也可以滿足，如圖7 (a)所示， 經過計算發現IK-Ea關系位于空間電荷區內，實際上大多數電子管都工作在這個區域. 因此可以判斷：如果實驗中的氣體閘流管能夠等效為理想二極管，那么二分之三關系應該成立.

其次，從Ea和IK測量準確性的角度考慮. 首先考慮Ea的測量，參考氣體閘流管的結構(圖2)，可以發現因為S和P的電荷分布不同， 可能會引入額外的電勢差，這樣就會使電子在等勢區內被加速，造成偏差，實驗中消除該偏差的方法是在S和P之間加入補償電壓Ec(實驗中為0.66 V)，調節Ec大小直到靈敏電流計上IS和IP同時出現. 事實上這個“同步”的判斷是通過人眼進行的，未必可以準確地確定Ec，因此，設計實驗探究Ec大小對于IK-Ea關系的影響，如圖7(b)和(c). 分別固定Ec=0和Ec=0.66 V(恰好補償)，計算得到2組數據斜率分別為1.21和1.22，十分接近而且偏離1.5較遠. 這說明Ec偏離實際值的解釋行不通. 同時，進行理論分析，S和P之間如果存在電勢差，會讓記錄的Ea小于或大于實際加速電壓，可能會導致式(7)中lnEa項變為ln (Ea-V′)，不過實驗證實，對于斜率的影響不大，可以忽略. 對于K和S之間存在的電勢差，使用類似的分析方法，也能排除K和S之間電勢差的影響. 參考文獻[5]給出這一電勢差約為0.4 V，其效果與S和P之間的類似，而且數值小于0.66 V，所以產生的影響應該可以忽略，因此可以排除Ea測量準確性的原因. 分析是否有可能是IK測量不準確造成實驗偏差. 參考圖2的氣體閘流管結構，提出假設:是否因為存在IM電流[如圖7(d)]或者打到外殼上的電流沒有辦法被收集，導致斜率偏小. 將閘流管拆開后發現M極板，外殼和S相連，因此假設不成立.

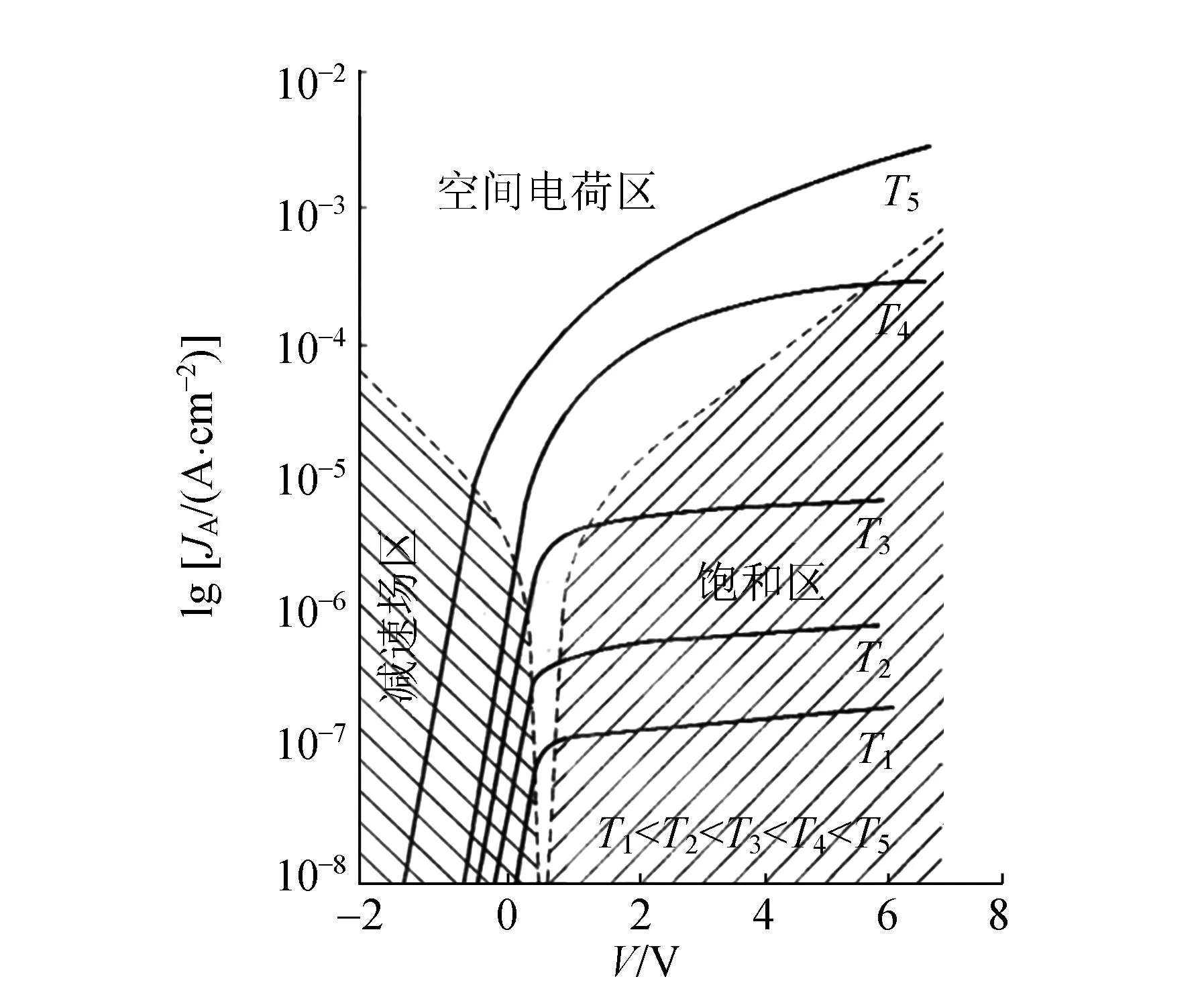
(a)理想二極管工作在空間電荷區的條件

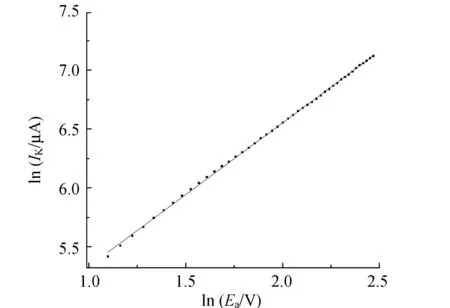
(b)Ec=0 V時電流電壓關系(直線斜率1.21)

(c)　Ec=0.66 V(恰好補償)時電流電壓關系　(直線斜率1.22)

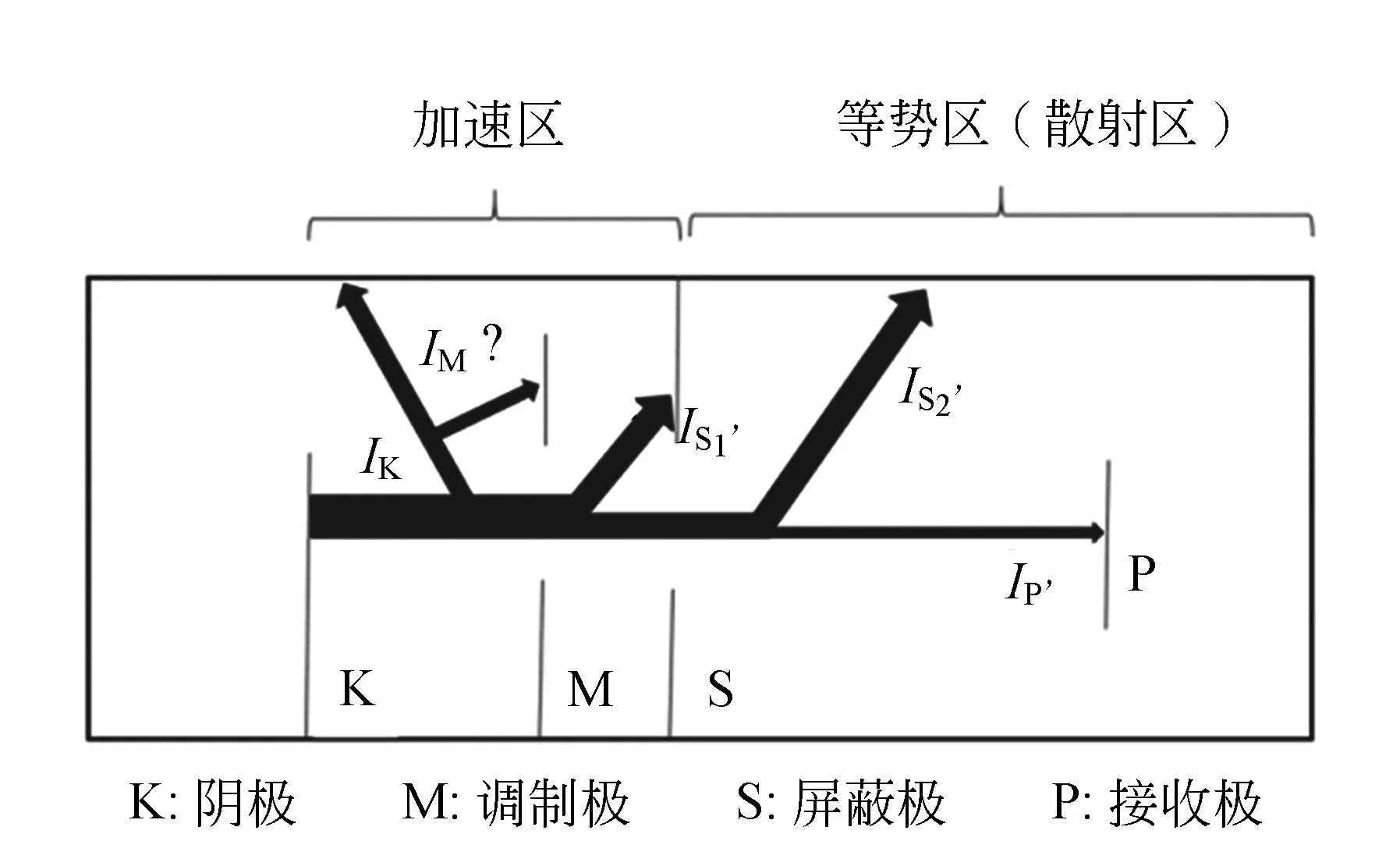
(d)假設IM的存在造成電流無法被全部收集圖7　分析偏離二分之三定律的可能原因

第三，在排除了IK和Ea測量不準確造成偏離后，發現開始的假設未必成立，把氣體閘流管近似為真空理想二極管較為粗糙，與實際偏差很大. 首先利用Drude模型分析工作在空間電荷區的理想二極管[6]，將電子視為小球，在電場中加速運動直至碰撞到氣體原子失去速度信息，得到

(8)

其中k和二極管結構有關，λ為平均自由程，

λ=1/Q,

(9)

只要λ不隨va變化，那么二分之三關系成立. 但是這里使用的Drude模型實際上僅僅在電子為自由電子氣的情況下成立，是完全的經典模型，弛豫時間τ由氣體原子數密度和氣體原子性質決定，和加速電壓沒有關系，根據式(9)散射截面應該和加速電壓也沒有關系. 而實驗中出現的冉紹爾-湯森效應，已經說明了散射截面隨著加速電壓的變化，經典的模型無法解釋. 所以嚴格地講，實驗中出現的電子受到氣體原子散射，不可以使用類似于Drude模型的方法去解釋，而是要考慮用電子在原子周期勢場中的波函數行為去解釋. 所以，只有在完全真空的情況下，2個模型刻畫的IK-Ea關系才相符，因此會產生IK-Ea關系的偏離. 參考文獻[1]認為對于低壓的氣體閘流管，電流也能很好地滿足二分之三定律，但實際上偏差很大.

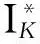
5結論

致謝：感謝樂永康老師對于陰極電流產生機理的點撥！

參考文獻：

[1]戴樂山，戴道宣. 近代物理實驗[M]. 北京：高等教育出版社，2006：78.

[2]O’Malley T F. Extrapolation of electron-rare gas atom cross sections to zero energy [J]. Physics Review, 1963,130(3):1020.

[3]顧恩遙，白翠琴，呂景林. 冉紹爾-湯森效應實驗儀自動化改進[J]． 物理實驗，2013，33(11)：11-15.

[4]胡永茂，張桂檣，李汝恒，等． 氙原子散射截面反常現象的觀測分析[J]． 物理實驗，2008，28(7)：40-44.

[5]Kukolich S G. Demonstration of the Ramsauer-Townsend effect in a xenon thyratron [J]. American Journal of Physics, 1968,36(8):701-703.

[6]陳博賢，劉光治，夏善紅，等. 平行平面形真空微電子二極管中的二分之三次方關系式[J]. 真空電子技術,2001(3):7-10.

[責任編輯：任德香]

Ramsauer-Townsend effect and the relation of its current and voltage

CAO Jun-zhi, YANG Xin-ju, YAO Hong-ying

(Department of Physics, Fudan University, Shanghai 200433, China)

Abstract:When electrons interact with rare gas in the thyratron, Ramsauer-Townsend effect will appear, which can’t be explained by the traditional model. The scattering cross-section will change as the speed of electron varies. The variation of geometric factor, scattering probability and total scattering cross-section were explored when the speed of electrons changed, then the Ramsauer-Townsend effect was demonstrated. Deviation from the Child-Langmuir law was observed, and possible explanation for it was researched. By using exclusive method, a possible explanation was found and demonstrated.

Key words:Ramsauer-Townsend effect; gas thyratron; Child-Langmuir law; total scattering cross-section

中圖分類號：O562.5

文獻標識碼：A

文章編號：1005-4642(2015)03-0001-05

作者簡介：曹鈞植(1992-)，男，上海人，復旦大學物理系2011級本科生.通訊作者：姚紅英(1966-)，女，遼寧遼陽人，復旦大學物理系講師，碩士，從事物理實驗教學工作.

收稿日期：2014-07-25；修改日期：2014-10-21