鐵耗對感應電機矢量控制的影響及其優化控制

陳永超，高相銘，林成棟

(1.安陽師范學院物理與電氣工程學院，河南安陽 455000;2.上海電機學院電氣學院，上海 200240）

1 引言

隨著電機驅動控制技術的發展，感應電機的矢量控制和直接轉矩控制技術得到了廣泛、深入的研究［1－2］，使感應電機的動態、穩態控制性能得到了大幅度的提高，甚至可以與直流電機的控制性能相媲美。就目前的研究而言，感應電機的控制策略大都建立在其傳統的動態等效數學模型基礎上，通常忽略感應電機鐵耗和電機參數的變化［3－4］，造成理論上可獲得高控制性能的控制策略在實際應用過程中無法獲得令人滿意的結果。隨著參數辨識技術的不斷發展，電機定、轉子各項參數都可以得到準確實時辨識，有效的解決了電機參數變化對電機控制性能的影響［5］。這使得鐵耗成為目前影響感應電機控制性能的最主要因素，特別在感應電機高速輕載運行時，采用忽略鐵耗的電機模型對電機控制性能會造成較大的影響。文獻［6－7］分析了感應電機矢量控制中，不考慮鐵耗的矢量控制使得感應電機轉子磁鏈幅值和轉子磁場定向角的估算存在一定的偏差，導致磁鏈與轉矩耦合，惡化了感應電機的矢量控制性能。為了得到更精確的控制，本文建立了在同步旋轉d－q坐標系下考慮鐵耗的感應電機動態等效數學模型，基于該模型分析了鐵耗對感應電機控制性能的影響并推導得到了矢量控制的優化控制算法。通過基于RT－Lab半實物平臺下的實驗，驗證了所提出優化算法的有效性。

2 考慮鐵耗的感應電機數學模型

感應電機的鐵耗可以分為定子鐵耗和轉子鐵耗，是同步旋轉磁場分別切割定、轉子使定、轉子鐵芯中磁通交變從而產生的磁滯損耗和渦流損耗之和［8］。其中磁滯損耗與磁場交變頻率成正比，渦流損耗與磁場交變頻率的平方成正比。當電機正常高速運行時，定子鐵芯中磁場交變頻率遠高于轉子鐵芯中磁場交變頻率，因此定子鐵芯中的渦流損耗是鐵耗的主要成因。

感應電機的鐵耗由主磁通密度決定，即與激磁電流有關，而與感應電機的負荷大小基本無關，因此可在決定激磁電流的電動勢兩端并聯一個電阻Rm用于等效感應電機的鐵耗［9］，并可根據坐標變換得到同步旋轉d－q坐標系下考慮鐵耗的感應電機等效電路，如圖1所示。

圖中Rs、ls分別為定子電阻、定子漏感;Rr、lr分別為轉子電阻、轉子漏感;φrd、φrq分別為兩相旋轉坐標系下d、q軸轉子磁鏈;Lm為激磁電感;w1為同步速度;wr為轉子轉速;Rm為等效鐵耗電阻;usd、usq分別為 d、q 軸定子電壓;isd、isq分別為 d、q軸定子電流;ird、irq分別為d、q軸轉子電流;ifed、ifeq分別為d、q軸流過等效鐵耗電阻的電流;imd、imq分別為d、q軸的激磁電流。

圖1對應的電壓方程為:

式中np為磁極對數，Lr為轉子自感。

3 鐵耗對感應電機矢量控制的影響

感應電機的矢量控制是基于轉子磁場定向的控制，其關鍵是獲得準確的轉子磁鏈位置，將定子電流解耦為轉矩分量和激磁分量，從而獲得較高的控制性能［10］。

感應電機在負載運行時，定子磁動勢F1可分成兩部分:產生氣隙主磁場Bm的激磁磁動勢Fm和抵消轉子磁動勢的負載分量 －F2，如圖2所示。對應地，定子繞組電流I1也可分成激磁電流Im和轉子負載電流－I2兩部分。當計及鐵芯損耗時，Bm在空間滯后于Fm以鐵耗角 αFe［11］。如果不考慮鐵耗，則圖2中不存在鐵耗角，激磁電流和氣隙主磁通的矢量在同一方向，激磁電流中不存在有功分量。

當考慮鐵耗時，在感應電機動態等效電路中增加了鐵耗等效電阻Rm，其中流過的電流ife是鐵耗等效電阻從定子電流中分得的。這說明考慮鐵耗后，感應電機的定子電流將有所增加，必須從電源側吸取更多的有功功率來彌補鐵芯中的損耗。

傳統的感應電機矢量控制器都是在忽略鐵耗的前提下設計的，而用不帶鐵耗補償的矢量控制器控制感應電機時，即使在電機參數辨識準確的情況下，實際的轉子磁鏈也會受鐵耗的影響，與矢量控制器計算出的轉子磁鏈存在偏差，使得轉子磁場定向不準確。當磁場定向角存在偏差時，會使得d、q軸各分量相互耦合，無法完全解耦。

傳統矢量控制中磁場定向的偏差如圖3所示，假設電機中實際的轉子磁場所在位置d軸，而采用忽略鐵耗的等效電路對轉子磁場的定向會有所誤差，轉子磁場估算位置在d’軸，偏差角度為θ。只要電機在正常運行就必然存在鐵耗，所以傳統磁場定向必然存在角度偏差。在一定負載下，隨著速度的上升鐵芯中磁通交變頻率增大，必然帶來鐵耗的增加，所以會導致偏差角度增大。當電機速度一定時，隨著負載的增加，鐵耗在有功功率中所占比重逐漸減小，磁場定向角度偏差就越小，磁場定向越精確。

由于轉子磁場定向的誤差一定存在，這會對d、q軸電流都有影響，所以無法分解得到最優的isd和isq。在閉環控制系統中，這將導致反饋的勵磁電流和轉矩電流分量與實際值不一致，從而對電機的動靜態性能產生一定影響。

根據式(7）可知，考慮鐵耗時的感應電機的實際輸出轉矩要小于不考慮鐵耗時的轉矩計算值。所以在傳統的矢量控制中，由于鐵耗的存在會消耗一部分電磁轉矩，從而使感應電機實際獲得的電磁轉矩比計算值偏小，這種鐵耗的阻尼作用使得傳統矢量控制的控制性能變差，降低了電機動態響應性能。

4 矢量控制的鐵耗補償優化

從式(13）中可以看出，與傳統的矢量控制不同，磁鏈分量與轉矩分量同時受到了轉子電流ird、irq的影響，激磁與轉矩分量不再解耦。傳統的矢量控制方法忽略了鐵耗等效電阻在這方面的影響，磁場定向與輸出轉矩的控制都是不準確的。當Rm趨向無窮大的時候，即忽略鐵耗的影響，由(13）可得:

可以看出，式(14）與傳統矢量控制完全一致。但是當鐵耗較大，即鐵耗等效電阻較小的時候，忽略Rm便會產生較大的定向誤差。

為了簡化控制算法，去掉式(12）中的微分項，就能夠在穩態條件下實現精確磁場定位控制，得到簡化的控制方案如下:

考慮鐵耗的矢量控制可參考傳統的磁鏈開環轉差頻率矢量控制系統。其基本控制思路是保持轉子的激磁電流分量不變，通過改變轉矩電流分量來改變轉差頻率，從而改變感應電動機的電磁轉矩［12］。

為了避免傳統矢量控制中由于忽略鐵耗而造成轉子磁場定向存在偏差，可利用式(15）對傳統的磁鏈開環轉差頻率型矢量控制系統進行優化。考慮鐵耗的矢量控制系統框圖如圖4所示。與傳統的轉差頻率矢量控制相比，只是在電流指令值計算環節增加了考慮鐵耗后的優化控制部分。因此從控制方案實現的角度考慮，并不需要做太多修改就可實現考慮鐵耗的矢量控制。由式(15）可以看出，同步轉速越高，進行優化控制需要補償的電流分量也越大。因此，鐵耗補償在電機高速輕載時運行時應該具有更明顯的優化效果。該優化控制方案能夠實現穩態下考慮鐵耗的精確轉子磁場定向，從而提高系統控制性能。

另外，在轉速磁通雙閉環的控制系統中，在對轉子磁通進行觀測時，為了更加準且的體現磁通的動態相應過程，不同于傳統矢量控制中轉子磁通幅值直接由isd獲得的方法，可以利用相電流采樣并進行park變換獲得isd和isq后，通過反解式(15）計算出imd，從而進一步計算得到ψr。

4 實驗驗證

為驗證考慮鐵耗矢量控制優化算法的有效性，對其進行實驗研究。實驗采用以RT－Lab為核心的半實物仿真平臺，仿真中除考慮鐵耗的矢量控制算法通過RT－Lab仿真器實現外，電機、逆變器、采樣電路等均通過實物實現。異步電動機參數如表1所示。

表1 感應電動機參數Tab.1 Parameters of IM

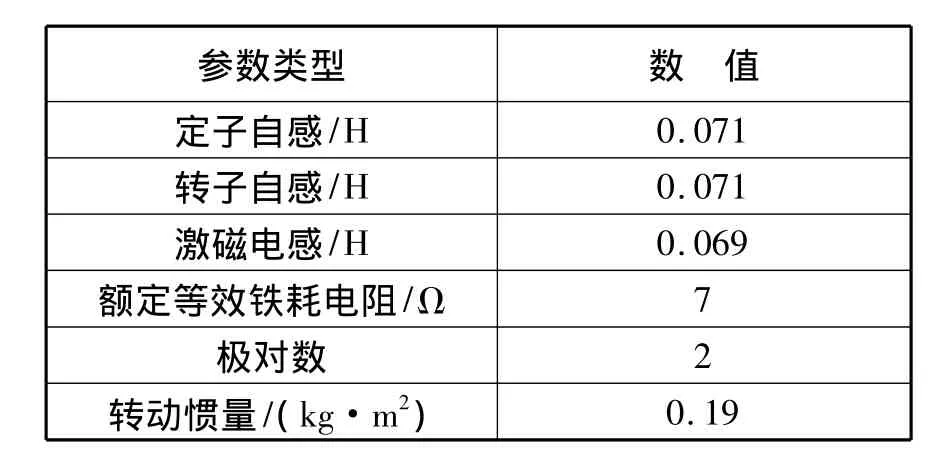
參數類型 數 值定子自感/H 0.071轉子自感/H 0.071激磁電感/H 0.069額定等效鐵耗電阻/Ω 7極對數2轉動慣量/(kg·m2）0.19

通過在上位機中利用Matlab/Simulink和RT－Lab軟件，完成建模、在線調參及信號監控等工作。另外用一臺Opal RT公司專為半實物仿真應用而設計的基于PC的實時仿真器作為目標機。目標機內部配置有四核處理器，運行QNX實時操作系統。由目標機完成模型的分布式實時計算、定子電流和相電壓的采樣、生成逆變器所需的PWM信號等工作。PWM信號利用Rt－Events工具箱中的RTE－PWM模塊產生，然后由數字板卡OP5252輸出。

通過速度階躍響應實驗來檢測補償效果，電機在空載條件下起動，轉速指令值為1400r/min。在0.4s時，給定速度指令階躍到1000r/min。應用鐵耗優化控制前后，電機轉速響應的波形如圖5所示。從圖中可以看出，經過鐵耗補償之后，速度響應性能有所改善，說明鐵耗優化補償有助于矢量控制性能提高。

實驗中給定轉子磁鏈值為0.7，電機穩態工作時A相定子電流如圖6所示。定子電流采樣后經park變換，由式(15）解出imd，然后由式(9）計算獲得轉子磁鏈波形如圖7所示。從圖中可以看出轉子磁鏈在指令值附近上下較小范圍內波動，證明考慮鐵耗的矢量控制優化補償算法能夠準確跟蹤轉子磁鏈指令值，反映出其對磁場有較好的定向能力。

5 結論

本文建立了考慮鐵耗的異步電動機等效動態數學模型，分析了傳統矢量控制中異步電動機鐵耗帶來的影響。為了避免由鐵耗導致轉子磁場定向不準確和電磁轉矩降低從而使電機的控制性能下降，本文根據考慮鐵耗的電機等效動態數學模型，推導得到了考慮鐵耗的優化補償算法，該算法簡單，便于工程實現。實驗結果表明進行鐵耗優化補償后，電機的動態、穩態響應性能有所改善，驗證了所提算法的有效性。

［1］崔納新，張承慧.變頻調速異步電動機效率優化控制的研究進展［J］.電工技術學報，2004，19(5）:36 －42.

［2］聶子玲，馬偉明，李衛超.矢量控制感應電動機H∞磁通觀測器研究［J］.電工技術學報，2006，21(8）:31－35.

［3］趙爭鳴，袁立強，孟朔 等.通用變頻器矢量控制與直接轉矩控制特性比較［J］.電工技術學報，2004，19(4）:81－84.

［4］張云，孫力，吳鳳江 等.考慮鐵耗的異步電動機模型及對矢量控制的影響［J］.電機與控制學報，2007，11(4）:359－363.

［5］張虎，李正熙，童朝南.基于遞推最小二乘算法的感應電動機參數離線辨識［J］.中國電機工程學報，2011，31(18）:79 －86.

［6］張云，孫力，吳鳳江 等.考慮鐵耗的感應電機模型及對矢量控制的影響［J］.電機與控制學報，2007，11(4）:359－363.

［7］Choi J W，Chung D W，Sul S K.Implementation of field oriented induction machine considering iron loss［C］.11th Annual Applied Power Electronics Conference and Exposition，1996:375 －379.

［8］羅應立，趙海森，姚丙雷 等.交流電機鐵耗的工程計算方法分析［J］.電機與控制應用，2010，(11）.

［9］李潔，鐘彥儒.考慮鐵損的感應電動機仿真模型研究［J］.系統仿真學報，2005，17(10）:330－337.

［10］李永東.交流電機數字控制系統［M］.北京:機械工業出版社，2002.88 －96.

［11］湯蘊璆，羅應力，梁艷萍.電機學［M］.北京:機械工業出版社，2009.162－168.

［12］阮毅，陳伯時.電力拖動自動控制系統［M］.北京:機械工業出版社，2012.188－189.