某型旋轉制導炸彈自旋頻率設計

段明寬，郭鴻武

(國防科技大學 機電工程與自動化學院，長沙410072)

?

某型旋轉制導炸彈自旋頻率設計

段明寬，郭鴻武

(國防科技大學 機電工程與自動化學院，長沙410072)

提出了將旋轉導彈單通道控制原理應用于制導炸彈控制系統設計的構想，并對旋轉制導炸彈自旋頻率設計進行了初步的探索。主要結合制導炸彈的運動特性，通過分析影響自旋頻率設計的主要因素，給出了自旋頻率的設計原則：避免產生滾轉共振，在飛行過程中保持動態穩定和考慮繼電式舵機的換向頻率。在此基礎上，以某旋轉制導炸彈為例，計算了其動力系數、固有頻率，最后得出了滿足設計要求的自旋頻率上限和下限。該設計方法也可應用于再入旋轉機動彈頭的自旋頻率設計。

自旋頻率；制導炸彈；旋轉炸彈

0 引言

20世紀60年代，戰術導彈家族中出現了一種旋轉導彈，它后來被廣泛地應用到各型反坦克導彈以及防空導彈上。旋轉反坦克導彈的典型代表型號有：美國的“標槍”反坦克導彈，俄國的“短號”反坦克導彈，英、法、德三國聯合研制的“崔格特”反坦克導彈等[1]。防空導彈的典型代表有：美國的“Stinger”系列導彈，美、德聯合研制的“拉姆”艦空導彈(RAM)以及俄羅斯研制的“IGLA”系列導彈等[2]。這類導彈通過使彈體繞其縱軸旋轉，達到簡化控制系統設計，穩定彈體飛行狀態，提高抗外界擾動能力和射向精度的目的[3-4]。

從公開的文獻資料來看，目前旋轉導彈的研究對象主要是反坦克導彈和防空導彈，將單通道控制原理應用于制導炸彈的相關研究文獻較少。目前制導炸彈的控制方式主要為側滑轉彎(STT)和傾斜轉彎(BTT)兩種控制方式[5-6]。其中STT控制方式較為成熟，工程設計和應用都比較廣泛，但是與BTT控制方式相比，其氣動效率較低，機動性能不夠好。雖然BTT控制技術相對STT控制技術具有很多優越性，但是限于當前的技術水平，尚不能完全取代STT控制技術[7]。而旋轉導彈具有抗外界干擾能力強、射向精度高、控制系統比非旋轉導彈簡單的優點，其可靠性也可以大大增強，系統總成本則大幅下降[4]。因此，本文設想在普通航空炸彈上安裝斜置彈翼，使炸彈在投放后產生自旋，將旋轉彈單通道控制原理應用于制導炸彈的控制系統設計中，提高控制效率和打擊精度，進一步降低制導炸彈生產成本，提高作戰效費比。

要實現旋轉炸彈的單通道控制，就必須選擇合適的自旋頻率。文獻[8]主要通過求解自旋導彈彈體運動的復數狀態方程，然后分析不同的自旋角速度對運動的穩態性能和動態過程的影響，最后得出在合理范圍內的自旋角速度。文獻[9-10]分別通過分析旋轉導彈彈體的頻率特性和動態穩定性，得出了旋轉導彈的動態穩定區及自旋速度范圍的確定原則。

本文在前述文獻對旋轉彈自旋頻率(角速度)的研究基礎上，將旋轉導彈單通道控制原理應用于制導炸彈的控制系統設計中，對其自旋頻率設計進行了初步的探索。主要結合制導炸彈的運動特性，通過分析影響自旋頻率設計的主要因素，給出了自旋頻率的設計原則，最后針對某型旋轉制導炸彈，計算了其滿足上述要求的自旋頻率的范圍。

1 影響旋轉制導炸彈自旋頻率設計的因素

影響旋轉制導炸彈自旋頻率設計的因素非常多，并且有些影響因素之間存在相互影響，甚至相互矛盾的關系，因此需要綜合考慮各種影響因素。下面列出了影響旋轉制導炸彈自旋頻率設計的一些主要因素。

1.1 制導炸彈的固有頻率

因為旋轉彈的控制力頻率和單體旋轉頻率是相同的，所以當自旋頻率和固有頻率接近或相同時，彈體就會發生共振，對彈體的結構產生破壞。經驗表明，旋轉導彈的自旋頻率必須超過彈體的固有頻率，如“賽格”反坦克導彈，其彈體固有頻率為1～2.5Hz，而其常溫自旋頻率則為8～9Hz[10]。

1.2 滾轉共振

旋轉炸彈投放后，當自旋頻率接近或者等于氣動俯仰頻率時，就會出現“滾轉共振”現象，甚至出現“共振聯鎖”現象，就極有可能導致配平攻角急劇增長，彈體橫向過載超過許用值而使彈體受到破壞[11]。

1.3 舵機換向頻率

如果旋轉炸彈自旋頻率過大，就會對操縱機構換向的快速性提出了很高的要求，導致操縱機構換向頻率過大，加大了部件的磨損，又或者會造成操縱機構來不及換向，使舵機不能很好地執行控制指令，進而使再入彈頭控制性能變差。

此外，由于彈體旋轉產生的馬格努斯效應，俯仰和偏航運動相互耦合，輸入誤差信號頻率等也會影響到自旋頻率的設計。因此在對旋轉彈頭的自旋頻率進行設計時，應綜合考慮以上各種因素。

2 旋轉制導炸彈自旋頻率的設計原則

2.1 避免產生滾轉共振

文獻[11]表明，當旋轉炸彈自旋頻率ωx與氣動俯仰頻率ωA接近或者相等時，就會發生滾轉共振；共振發生后，如果兩者的變化趨勢在較長時間內幾乎相同，就會發生“共振聯鎖”，有可能導致配平攻角急劇增長，橫向載荷過大而使炸彈受到破壞。

設λ為自旋比，令

(1)

由文獻[11]知，設

Z=λμ+i(λ2-1)

(2)

其中i為虛數單位，μ為阻尼項。

配平攻角放大系數A為

(3)

相對于無滾配平角的滯后角Δψ是復數Z的實部與虛部的四象限反正切值，在matlab中，其計算方法為

Δψ=αtan2(imag(Z),real(Z))

(4)

下面分析自旋比λ對A和Δψ的影響。在式(3)和式(4)中針對不同的μ，可以得出A和Δψ隨自旋比λ的變化曲線如圖1所示。

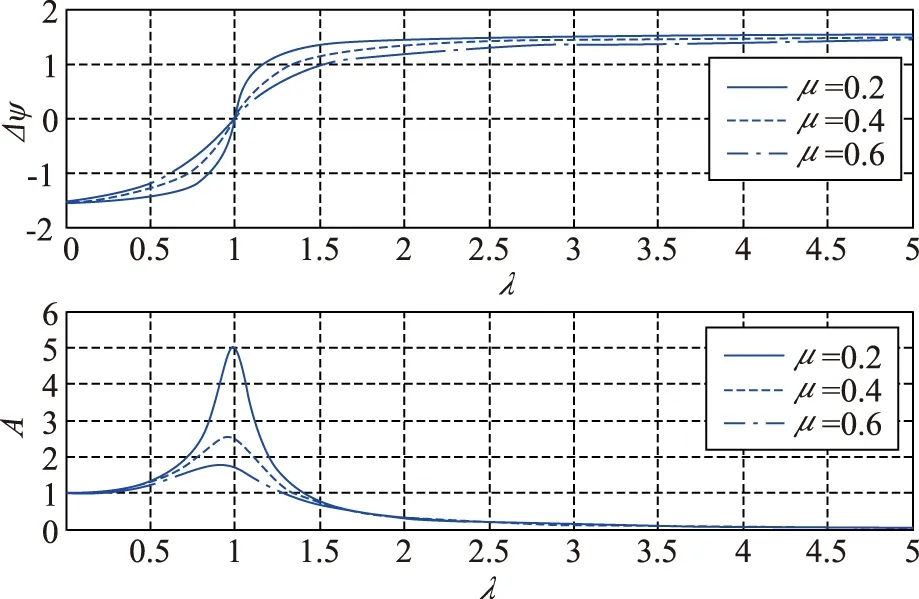
圖1 自旋比λ對Δψ和A的影響曲線Fig.1 The influencing curves of λ on Δψ and A

由圖1可知，當自旋比λ在0和2之間時，A和Δψ的變化較為劇烈；當自旋比λ大于2時，λ的繼續增大對A和Δψ的影響變化不大。

2.2 旋轉制導炸彈的動態穩定區

由文獻[9，12]中可知，炸彈的固有角頻率為

(5)

其中，a22為炸彈的空氣動力阻尼系數，a24為炸彈的恢復動力系數，a34為炸彈的法向動力系數，計算公式為：

(6)

(7)

(8)

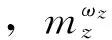
為保證其投放后滑行過程中的動態穩定性，應滿足[10]

(9)

其中，q為動壓。令

(10)

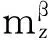
ωc-Cωx>0

(11)

令fc為炸彈的固有頻率，fx為炸彈的自旋頻率，單位均為Hz，且

(12)

(13)

則式(11)可變換為

fc-Cfx>0

(14)

式(14)是一個線性不等式，由此可知，若炸彈的自旋頻率fx大于一定值時，則會產生動不穩定，因此可以利用式(14)確定炸彈在投放后滑行過程中，使其保持動態穩定的自旋頻率的上限。

3 某旋轉制導炸彈自旋頻率設計

由文獻[11]可知，氣動俯仰頻率ωA的計算公式為

(15)

由式(1)和式(15)，令

(16)

其中，J=Jy=Jz?Jx，由2.1節知λ的值應大于2。

由式(14)，令

(17)

(18)

以某旋轉制導炸彈為例，彈體質量為280kg，初始速度為200m/s，投放高度為8000m。從已有的氣動力數據可以得到動力系數，如圖2所示。

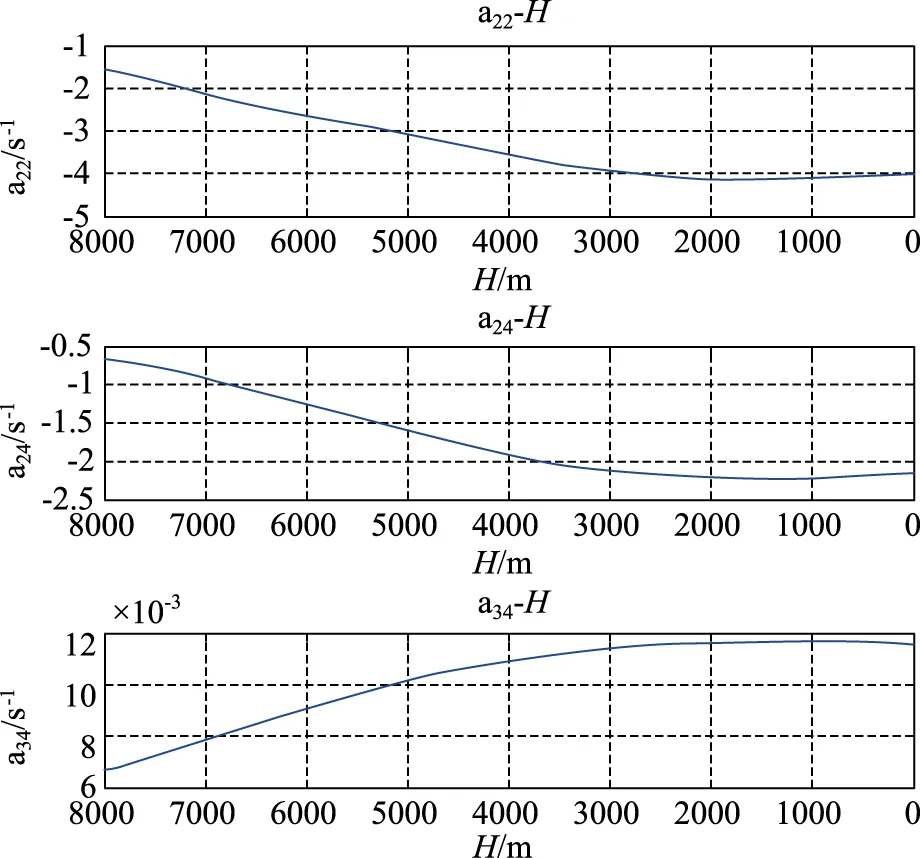
圖2 動力系數隨高度的變化曲線Fig.2 The curves of power coefficient varying with height

利用式(5)、式(10)和式(12)可以得到旋轉制導炸彈的固有頻率fc和穩定邊界常數c，如圖3所示。

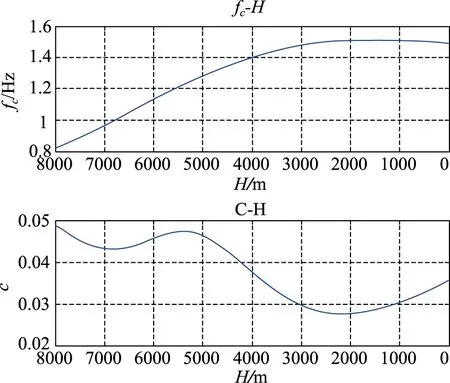
圖3 固有頻率fc和常數c隨高度的變化曲線Fig.3 The curves of the natural frequency fcand the constant c varying with height

由式(12)、式(16)、式(17)和式(18)可得到如圖4所示的某旋轉制導炸彈自旋頻率的上、下限fxmin和fxmax的變化曲線。

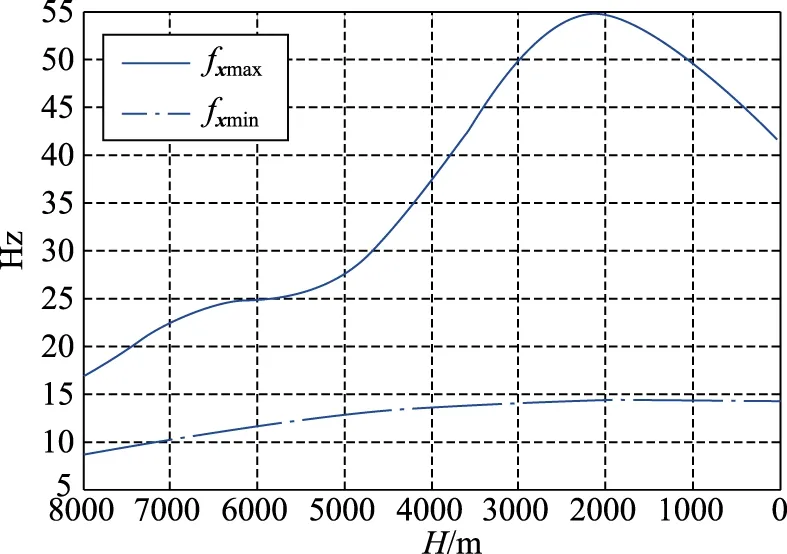
圖4 某旋轉制導炸彈自旋頻率上下限Fig.4 The upper and lower limits of self-spin frequency of a certain rotating guided bomb

由圖3可知，此制導炸彈的固有頻率約為0.8～1.5Hz之間。按照旋轉制導炸彈自旋頻率的設計原則，由圖4可知此旋轉制導炸彈的初始自旋頻率設計為8～17Hz之間，隨著彈頭的飛行，速度逐漸增大，其自旋頻率會逐漸的增大，但是最小不得超過15Hz，最大不得超過54Hz。現有的防空導彈繼電式舵機一般就可以滿足本文的設計需求，如“箭-2M”的舵機舵面由-15°轉到+15°需時為4～5ms，舵機延遲時間小于4ms，其換向頻率可達56～63Hz，顯然能夠滿足本文的設計需求[13]。

4 結束語

本文給出了影響旋轉制導炸彈自旋頻率設計的主要因素，同時給出了自旋頻率的設計原則，最后以某旋轉制導炸彈為例進行自旋頻率設計，計算了其動力系數、固有頻率，最后得出了其自旋頻率的上限和下限，炸彈模擬飛行試驗表明，該設計較為合理。本文所采用的設計方法也可應用于再入旋轉機動彈頭的自旋頻率設計。

[1] 王狂飆.旋轉導彈制導技術及應用[J].彈箭與制導學報，2002，22(3)：28-31.

[2] 張平峰，周志超.鴨式布局旋轉導彈氣動特性研究[J].上海航天，2013，30(3)：45-49.

[3] 鄭新，傅維賢，趙民.滾轉彈道導彈運動規律與控制研究綜述[J].航天控制，2011.2，29(1)：93-98.

[4] 李惠芝，成楚之.旋轉導彈的氣動布局[J].戰術導彈技術，1989.9，(3)：4-10.

[5] 李昕.制導炸彈制導控制技術研究[D].知網碩博論文庫，2009.

[6] 郭正勇.BTT滑翔增程制導炸彈制導控制系統的設計與仿真[D].知網碩博論文庫，2010.

[7] 趙靖男，趙興鋒，鄭志強.BTT導彈的發展現狀與趨勢[J].飛航導彈，2006，(10)：37-39，43.

[8] 汪樹和.自旋導彈彈體自旋角速度的確定[J].船工學報，1980，(2)：15-29.

[9] 張有濟.戰術導彈飛行力學設計(下)[M].北京：宇航出版社，1998：389-396.

[10] 錢杏芳，林瑞雄，趙亞男.導彈飛行力學[M].北京：北京理工大學出版社，2012：255-263.

[11] 王國雄，馬鵬飛.彈頭技術[M].北京：宇航出版社，1993：338-357.

[12] 張有濟.戰術導彈飛行力學設計(上)[M].北京：宇航出版社，1998：196-198.

[13] 葉堯卿.便攜式紅外尋的防空導彈設計[M].北京：宇航出版社，1996：134-136.

Design of Self-spin Frequency for Rotating Guided Bomb

DUAN Ming-kuan，GUO Hong-wu

(The Institute of Electromechanical Engineering and Automation，National University of Defense Technology，Changsha 410072，China)

In this paper，the principle of the single channel control of rotating missile is applied to the design of the control system in guided bomb，and the self-spin frequency for rotating guided bomb is designed.By analyzing the main influencing factors on self-spin frequency design combine with the characteristics of guided-bomb movement，the design principles are given in this paper：avoiding roll resonance，maintaining dynamic stability during the process of flight and considering the reversing frequency of the relay control actuator.On this basis，this paper takes a rotating guided bomb as an example of designing self-spin frequency，calculating its dynamic coefficient，natural frequency and giving its self-spin frequency of upper and lower limits finally.The method in this paper can also be used in designing the self-spin frequency of the reentry rotating maneuvering warhead.

Self-spin frequency；Guided bomb；Rotating bomb

2015 - 04 - 02；

2015 - 05 - 18。

段明寬(1985 - )，男，碩士研究生，研究方向為精確制導與控制。

TP273

A

2095-8110(2015)05-0009-05