基于粒子群算法的偽衛星布站優化設計

李東新，彭 云，常 青，李 晶，于 淵

(1.北京航空航天大學 電子信息工程學院，北京100191；2.北京航天長征飛行器研究所，北京100076；3.交通信息通信技術研究發展中心，北京100011)

?

基于粒子群算法的偽衛星布站優化設計

李東新1，3，彭 云2，常 青1，李 晶3，于 淵3

(1.北京航空航天大學 電子信息工程學院，北京100191；2.北京航天長征飛行器研究所，北京100076；3.交通信息通信技術研究發展中心，北京100011)

針對偽衛星布站問題，采用粒子群智能優化算法，以導航定位中精度因子作為粒子群適應度函數，采用線性遞減慣性權值策略，通過適當次數的進化與迭代，最終尋找到最優化的偽衛星布站設計方案。通過對兩條豎直平面內的拋物線軌跡進行仿真驗證，結果表明，基于粒子群算法的偽衛星布站優化設計方案可以減小全程精度因子，提高了偽衛星獨立定位系統的定位精度。

粒子群算法；線性遞減慣性權值策略；偽衛星布站

0 引言

衛星導航定位的基本作用是向各類用戶和運動平臺實時提供準確、連續、可靠的位置、速度和時間信息。當前各種全球導航衛星系統，其系統的精度、可靠性和可用性都在一定程度上依賴于可跟蹤衛星的數量以及幾何分布情況。由于受到以上因素的制約，在峽谷、室內以及地下等比較苛刻的觀測環境下，可視衛星的數量和幾何布局就不能滿足定位的需求。同時，由于用戶與導航衛星之間的距離一般都比較遠，信號衰減較大，導航信號到達地面時都比較弱，在復雜電磁環境下，極易受到干擾而無法使用。位于地面的偽衛星系統就能夠更好解決這個問題。國內外學者在這一領域進行了深入的研究，相關的研究成果已經初步應用于露天礦邊坡變形監測、壩體變形監測以及建筑物變形監測等領域，并產生了良好的效益[1-4]。

偽衛星不僅可以輔助GNSS導航定位，而且因為其自身功能和原理與導航衛星類似，且具有設置靈活機動，抗干擾性能好等優點，所以在特定環境，可以完全替代導航衛星，進行獨立定位。偽衛星系統中，偽衛星的幾何分布情況對用戶導航定位精度具有重要影響，偽衛星布站技術是偽衛星系統設計的關鍵技術之一，在偽距測量誤差一定的情況下，偽衛星良好的幾何位置分布可以大大減小導航定位誤差，提高定位精度。

粒子群優化算法(Particle Swarm Optimization，PSO)是Kennedy和Eberhart[5]于1995年提出的一種全局優化進化算法，其思想來源于對鳥群捕食行為的研究，同遺傳算法和蟻群算法相比，PSO有著算法簡單、容易實現，并且可調整參數少等特點，因此被廣泛應用于結構設計[6]、電磁場[7]和任務調度[8]等工程優化問題中。

在本文中，我們采用粒子群優化算法對偽衛星獨立定位系統中偽衛星的幾何位置進行優化，并用兩條豎直平面內的拋物線軌跡進行導航定位幾何精度因子仿真試驗，仿真結果表明，采用基于改進的粒子群布站優化算法能夠大大減小導航定位精度因子，提高了定位精度。

1 偽衛星定位原理

偽衛星定位原理同衛星導航原理類似，利用到達時間測距原理來確定用戶的位置。偽衛星定位原理如圖1所示。

圖1 偽衛星定位原理圖Fig.1 Principle of pseudo-satellite positioning

接收機測量偽衛星發射信號與接收機接收到信號之間的時間差Δt，乘以光速c便可求得距離ρ(ρ=cgΔt)。由于偽衛星系統時鐘和接收機時鐘并不完全同步，存在時鐘偏移誤差，設這個誤差為δtu。一般偽衛星布設在地面或對流層以內，電磁波必然要通過對流層，由于對流層引起測量誤差設為T，則用戶相對于偽衛星i的觀測方程為

ρi=ri+c·(δtu-δti)+Ti+εi

(1)

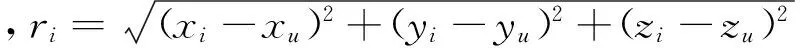
ρi-Ti+cgδti-εi=

(2)

其中含有4個未知量，通過接收到至少4顆偽衛星信號聯立求解，就可以單獨實現導航定位。

2 精度因子DOP

雖然偽衛星定位原理和GNSS導航定位原理相似，但由于偽衛星布站區域僅限于對流層到地平面區域，大多數偽衛星平臺都直接安裝在地面，組成地基偽衛星網，偽衛星布局受限，從而造成偽衛星獨立定位系統中定位精度很差，嚴重影響偽衛星系統的可用性和性能。

在衛星導航定位系統中，有很多方法可以評定偽衛星的幾何分布結構對定位精度的影響，精度因子(DilutionofPosition，DOP)由于計算較為簡單并且表達直觀，成為其中較為常用的一種衡量尺度。在同等用戶等效距離誤差的條件下，DOP值越小，往往代表星座分布結構越好，定位精度越高。通過對已知衛星幾何分布下空間內各點的DOP的仿真計算，可以得到對相應分布結構的評價結果，以此作為設計、選擇偽衛星組網方式好壞的判斷依據。

設用戶接收機的位置為(xu，yu，zu)，第i顆偽衛星的位置為(xi，yi，zi)(i=0，1，…，n，n為偽衛星數目)。由偽衛星的幾何分布可以首先得到觀測矩陣如下[9]

(3)

其中，(axi，ayi，azi)為從用戶接收機(即需要計算DOP的位置)指向第i顆衛星的單位矢量。單位矢量的計算式如下

(4)

得到觀測矩陣G后，可以由此得到權系數矩陣H如下

(5)

而相應的各種DOP值都可以根據權系數矩陣H計算得到。

常用精度因子有幾何精度因子(GDOP)、位置精度因子(PDOP)、水平精度因子(HDOP)、垂直精度因子(VDOP)和時間精度因子(TDOP)。幾何精度因子GDOP反應了空間位置誤差和時鐘誤差的綜合影響；空間位置精度因子PDOP反應了空間位置誤差的影響；水平位置精度因子HDOP反應了水平位置誤差的影響；垂直位置精度因子VDOP反應了垂直位置誤差的影響；時間精度因子TDOP反應了時鐘誤差的影響，其表達式分別如下

(6)

由式(6)，我們有了評價精度因子的指標，可以看出精度因子只與用戶位置和偽衛星位置有關，根據不同的要求，取不同的精度因子，為粒子群優化中的適應度函數，則可以找到對應的最優的偽衛星布站方案。

3 基于粒子群算法的偽衛星布站優化方法

3.1 基本粒子群優化方法

在基本的粒子群算法中，先在可行解空間中隨機初始化n個粒子構成初始種群，并為每個粒子隨機初始化一個速度，每個粒子都對應優化問題的一個解，并由目標函數為之確定一個適應值，而速度用來決定粒子在解空間中的運動。在算法的每次迭代中，粒子將跟蹤自身從開始到當前找到的自身最優解和種群當前找到的最優解，逐代搜索，直到最后得到最優解。

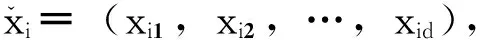
(7)

其中，c1和c2稱為加速度因子，通常取為2；R1與R2為均勻分布于[0，1]之間的隨機數，且相互獨立；a稱為約束因子，通常為1；ω為慣性權值，通常取為1。

式(7)為粒子群算法基本算法，即基本粒子群算法。基本PSO算法早期收斂速度非常快，但卻暴露出局部搜索能力差的缺點，這使得算法后期收斂速度緩慢且求解精度降低。

為了改進粒子群算法，使得開始迭代時盡可能在較大范圍內搜索，避免陷入局部最優解，當迭代到達一定階段后，縮小迭代范圍，在較小范圍內迭代求解，提高求解精度，Shi等[10]進一步提出了LDIV策略，即在迭代過程中線性地減小慣性權值，并表示為

(8)

其中，ωmax、ωmin分別表示優化過程中慣性權值的最大最小值，N表示最大迭代次數，np表示當前已迭代的次數。通過線性遞減慣性權值，提高了優化算法性能，減少迭代次數，提高了精度，本文采用線性遞減粒子群算法來優化偽衛星布站問題。

3.2 基于粒子群算法的布站優化設計

基于粒子群算法的優化布站設計主要分以下幾步：

1)初始化。確定可布站分布范圍和需要布站的偽衛星數目，取所有偽衛星三維位置坐標值的組合作為每個粒子的位置，在可布站分布范圍內隨機初始化粒子的位置矢量和速度矢量，偽衛星數目至少為4。并將粒子當前位置初始化為該粒子歷史最優解，以所需DOP因子為適應度函數，尋找當前DOP最小的粒子位置為全局最優解。

2)逐步迭代。按照式(7)和式(8)，進行粒子位置和速度進化，在更新位置過程中，我們要不斷對每個粒子的各維位置坐標進行檢測，若大于所限定區域上界，則約束為上界；若小于所限定區域下界，則約束為下界，這樣使得粒子不超出所限定區域。同時，對DOP因子的計算過程涉及到矩陣求逆，在求逆之前應先檢測矩陣是否可逆，對于不可逆的結果定義為無效位置，不參與最優解計算與比較，繼續下一次迭代。

3)更新最優解。每次迭代后都要重新計算各個粒子的適應度(這里指所要求優化目標的DOP值)。對每個粒子當前適應度和該粒子歷史最優適應度進行比較，若優于歷史最優適應度，則更新該粒子的最優解。最后，選出粒子群的最優適應度作為全局最優解。

4)算法結束。當到達優化迭代次數或者達到求解精度后結束迭代，當前全局最優解即為最優布站方案。

算法流程如圖2所示。

圖2 基于粒子群算法的偽衛星布站優化設計流程圖Fig.2 Flow chart of pseudo-satellite stationoptimization design based on particle swarmoptimization algorithm

4 仿真分析

根據一種最基本的偽衛星定位系統的設計，采用4～5顆偽衛星組成偽衛星網絡，在本次仿真中，對坐標系的定義進行說明如下：坐標系用o0x0y0z0表示，坐標原點用o0表示，o0x0軸在坐標原點的水平面內，指向瞄準方向；o0y0軸沿過坐標原點的鉛垂線，與o0x0軸垂直且指向上；o0z0軸與o0x0軸及o0y0軸形成右手直角坐標系。在以上坐標系中，偽衛星布局范圍(-300，0，-300)，(-300，0，300)，(60，0，-300)，(60，0，300)(單位：km)。目標優化軌跡為從兩條從原點出發在xoy平面內以拋物線方式前進一段距離。由于最遠端對應精度因子最差的點，以軌跡最遠端(坐標(300，10，0))為優化點，以此來實現對整條軌跡的優化。

1)4顆陸基偽衛星(Y=0)，以HDOP為粒子群適應度函數，迭代次數200次，偽衛星布站優化結果如表1所示(坐標單位為km)。

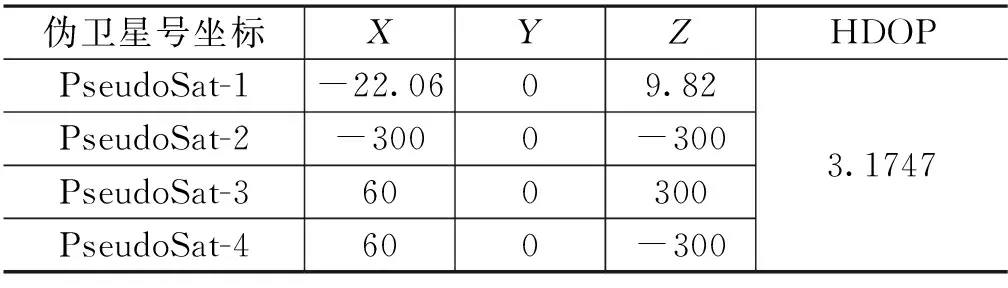
表1 4顆陸基偽衛星、HDOP為適應度函數的布站優化結果Tab.1 Optimization results of pseudo-satellite stationby 4 ground-based pseudo-satellites and HDOP as the fitness function

以表1優化結果為偽衛星位置，對遠近兩種軌跡的HDOP進行仿真，結果如圖3所示。

由圖3可以看出，優化后的偽衛星布站可以使得較近軌跡上的HDOP在1.6～2.18，較遠軌跡上的HDOP在1.6～3.17，已經達到了可以與GPS導航衛星相比擬的程度，可以滿足工程對水平方向定位精度要求的需求。

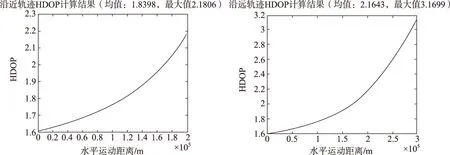
圖3 沿著近軌跡和遠軌跡HDOP仿真曲線圖Fig.3 Simulation curves of HDOP along the track of near and far trajectories

2)4顆陸基偽衛星(Y=0)，以PDOP為粒子群適應度函數，迭代次數200次，偽衛星布站優化結果如表2所示(坐標單位為km)。

表2 4顆陸基偽衛星、PDOP為適應度函數的布站的優化結果Tab.2 Optimization results of pseudo-satellitestation by 4 ground-based pseudo-satellites and PDOP as the fitness function

以表2優化結果為偽衛星位置，對近軌跡和遠軌跡的HDOP、VDOP、GDOP進行仿真，結果如圖4所示。

由圖4中6個仿真圖可以看出，以定位精度因子PDOP為粒子群適應度函數情況下，在水平方向定位精度比以HDOP為適應度函數求解得水平方向精度稍差，由于偽衛星都布設在地面，垂直方向精度因子都比水平方向精度因子大很多，說明地基偽衛星不適用于高程定位。通過粒子群算法優化，可以保證在較近仿真軌跡上，垂直精度因子小于32；在較遠仿真軌跡上，垂直精度因子小于55。也說明在遠離偽衛星區域的地表附近，定位精度急速惡化，此時應采用其他方法彌補偽衛星高程定位的不足，以確保飛行器全程導航定位。

3)3顆陸基偽衛星(Y=0)，1顆高程20km以內空基偽衛星(0km≤Y≤20km)，以PDOP為粒子群適應度函數，迭代次數200次，偽衛星布站優化結果如表3所示(坐標單位為km)。

表3 3顆地基偽衛星和1顆空基偽衛星、PDOP為適應度函數的布站的優化結果Tab.3 Optimization results of pseudo-satellite station by 3 ground-based and 1 air-based pseudo-satellites and PDOP as the fitness function

以表3優化結果為偽衛星位置，對較近仿真軌跡和較遠軌跡的HDOP、VDOP、GDOP進行仿真，結果如圖5所示。

圖4 沿著近軌跡和遠軌跡HDOP、VDOP和PDOP仿真曲線圖Fig.4 Sinulation curves of HDOP，VDOP and PDOP along the track of the near and far trajectories

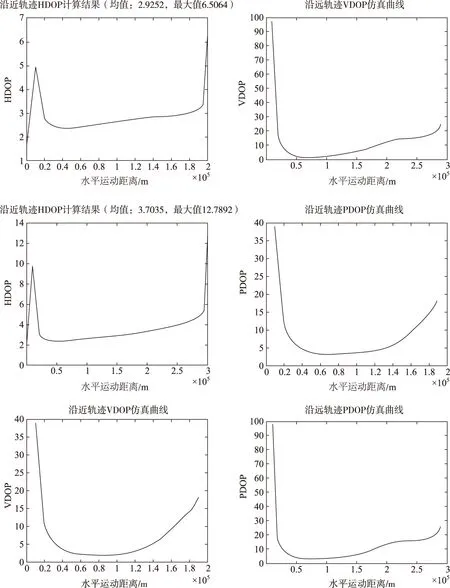
圖5 沿著近軌跡和遠軌跡HDOP、VDOP和PDOP仿真曲線圖Fig.5 Simulation curves of HDOP，VDOP and PDOP along the track of the near and far trajectories

由圖5中6個仿真曲線圖可以看出，增加1顆空基偽衛星后，除去軌跡起始點和終止點處，全程VDOP和PDOP有一定改進，HDOP有一定的惡化。增加空基偽衛星后，提高了高程定位精度，從而用戶三維定位精度都有所提高，但是空基偽衛星需要將偽衛星放置于20km高空，會有飛行器移動的動態造成用戶測距困難，可能引入較大誤差。

從以上仿真結果可以看出，基于粒子群算法的偽衛星布站優化方案，可以根據不同指標要求和不同布站環境下尋找出較優化的偽衛星布站方案，從而證實了本文所提出方案的可行性。

5 結論

通過本文所述線性遞減權值粒子群優化算法，對偽衛星布站進行優化設計，針對不同適應度函數，優化得出滿足不同要求的偽衛星布站方案，大大提高了偽衛星獨立導航定位系統的定位精度，提高了偽衛星系統的性能，本文方案對偽衛星布站設計具有重要的工程應用價值。

[1] Choudhury M，Rizos C.Slow structural deformation monitoring using Locata-A trial at Tumut Pond Dam[J].Journal of Applied Geodesy，2010，4(4)：177-187.

[2] Bonenberg L K，Hancock C，Roberts G W.Locata performance in a long term monitoring[J].Journal of Applied Geodesy，2013，7(4)：271-280.

[3] Jianpeng W，Jingxiang GAO，Chao LIU，et al.High precision slope deformation monitoring model based on the GPS/Pseudolites technology in open-pit mine[J].Mining Science and Technology，2010，20(1)：126-132.

[4] Montillet J P，Meng X，Taha A，et al.Achieving centimeter-level positioning accuracy in urban canyons with locata technology[J].Positioning，2007，1(12).

[5] Kennedy J.Particle swarm optimization[M].Encyclopedia of Machine Learning.Springer US，2010：760-766.

[6] Elegbede C.Structural reliability assessment based on particles swarm optimization[J].Structural Safety，2005，27(2)：171-186.

[7] Robinson J，Rahmat-Samii Y.Particle swarm optimization in electromagnetics[J].Antennas and Propagation，IEEE Transactions on，2004，52(2)：397-407.

[8] Salman A，Ahmad I，Al-Madani S.Particle swarm optimization for task assignment problem[J].Microprocessors and Microsystems，2002，26(8)：363-371.

[9] GPS原理與接收機設計[M].電子工業出版社，2009.

[10] Shi Y，Eberhart R C.Empirical study of particle swarm optimization[C].Evolutionary Computation，1999.CEC 99. Proceedings of the 1999 Congress on.IEEE，1999，3.

Optimal Design of Pseudo-satellite Station Based on Particle Swarm Optimization Algorithm

LI Dong-xin1，3，PENG Yun2，CHANG Qing1，LI Jing3，YU Yuan3

(1.Electronic and Informational Engineering Institute，Beihang University，Beijing 100191，China；2.Beijing Institute of Space Long March Vehicle，Beijing 100076，China；3.R&D Center of Traffic Information and Communication Technology，Beijing 100011，China)

For pseudo-satellite station problem，we adopt the particle swarm algorithm which has the function of intelligent optimization.We use the accuracy factor of navigation and positioning as the fitness function of the particle swarm，with a linear decreasing inertia weight strategy and the appropriate number of evolution and iterative，eventually to find optimal design of pseudolite station.We use two parabolic trajectories in the vertical planes for simulation，the results show that，the station design scheme for pseudo-satellite based on particle swarm optimization algorithm can reduce the whole precision factor，and improve the positioning accuracy of independent pseudo-satellite positioning system.

Particle swarm algorithm；Linear decreasing inertia weight strategy；Pseudo-satellite station

2015 - 07 - 15；

2015 - 08 - 13。

國家863項目基金(2013AA122403)

李東新(1989 - )，男，碩士，主要從事擴頻通信，衛星導航，信息處理方面的研究。

E-mail：lidx2013@buaa.edu.cn

TN967.1

A

2095-8110(2015)05-0044-08