永磁同步電機的狀態解耦控制研究

楊 貴,彭顯剛

(廣東工業大學 自動化學院, 廣州 510006)

永磁同步電機的狀態解耦控制研究

楊 貴,彭顯剛

(廣東工業大學 自動化學院, 廣州 510006)

針對永磁同步電機系統耦合問題,通過Park和Clarke坐標變換得到基于d-q軸坐標模型,建立了永磁同步電機的非線性狀態方程數學模型。應用反饋解耦控制控制方法,實現了永磁同步電機相電流和相電壓的解耦控制。仿真結果表明,狀態反饋解耦控制方法有效地實現了電機相電壓、相電流的解耦控制,且具有較好的動靜態性能及靈活、方便特點。

永磁同步電機;解耦;反饋控制

稀土永磁材料的發展及電力電子技術的進步,促進了永磁同步電機的發展[1, 2]。永磁同步電機具有氣隙磁密度高,體積小,功率因數高,起動轉矩大等特點,在工業自動化、數控機床、鐵路運輸、船運領域得到了廣泛應用[3-5]。近年來,許多新的非線性系統控制方法用于永磁同步電機的解耦,如自適應控制、模糊神經網控制、智能解耦、逆系統解耦控制[6-10]。但自適應解耦、智能解耦理論尚不完善,在工程應用中,由于算法太復雜難以實現較好的解耦[8, 11]。逆系統解耦控制對于低階系統,靜態解耦比較簡單,但對于高階系統求逆十分困難。因此,尋找簡單易行的有效解耦方法是現在普遍關注的問題[12]。工程上,目前主要采用矢量控制技術實現解耦,現研究成熟的矢量控制解耦技術有:前置補償解耦方法,前置矩陣對角化系統解耦方法。前置補償矩陣局限于單定子永磁同步電機,前置矩陣對角化系統解耦對原系統矩陣必須為非奇異矩陣[9]。鑒于此,本文提出一種有效的矢量控制策略,即對永磁同步電機進行坐標變換,得到在d-q軸為坐標的數學模型的狀態方程,再應用狀態反饋控制策略實現解耦[13]。最后在Matlab-Simulink平臺上建立仿真永磁同步電機模型,驗證狀態反饋解耦控制方法在永磁同步電機上的解耦效果。

1 狀態反饋解耦控制

解耦控制是通過一定的控制算法將控制對象中的輸入輸出耦合消除使控制對象中的輸出僅受相應自身輸入的控制。一個線性時不變系統用反饋解耦控制方法來解耦[9-10], 引入反饋解耦矩陣F和輸入變換矩陣G,多變量狀態反饋解耦原理如圖1所示。

U=FX+GU′

(1)

式中：U′ 表示新的“m”維輸入控制矢量。

解耦得:

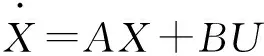
Y=CX

(2)

其中，X∈Rn,U∈Rm,Y∈Rm,w∈Rm，m≤n狀態反饋解耦控制方法,可以存在多個{F,G}解。解的獲得取決于所需要的傳遞函(Hi(p),i=1,2…m)。F為m×n維矩陣,G為m×m維矩陣。

圖1 多變量狀態反饋解耦原理圖

Fig.1 Schematic diagram of the multi variable state feedback decoupling

由圖1可得到,設定新的系統傳遞函數Hdiag為

此傳遞函數實現了永磁同步電機相電壓相電流一一對應關系,實現了系統解耦。

2 應用在三相永磁電機的狀態反饋解耦控制

永磁同步電機通過坐標變換,使其為直流電動機。矢量控制技術利用坐標變換方法,實現了電機定子力磁分離與轉矩的解耦。三相永磁電機的坐標變換原理如圖2所示[14]。

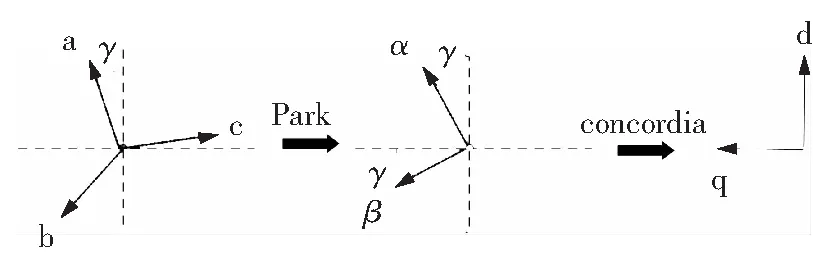
圖2 坐標變換原理圖

(3)

可看出d-q軸電流分量Id、Iq相互耦合,不便于電流控制。應用狀態反饋控制解耦技術可解決此問題,式(3)中的模型變化等效同:

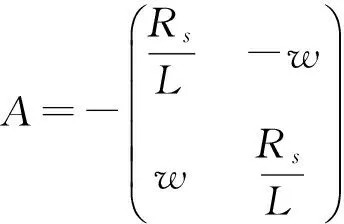
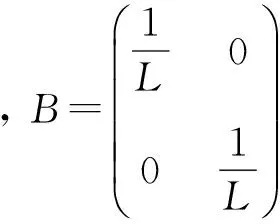
(4)

{F,G}的求解基于以下條件[15-16]:

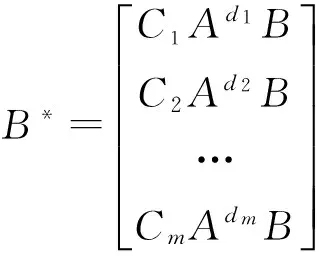
(5)

di是非負整數且滿足條件：

di=min{j:CiAjB≠0；j=0,1,…,n-1} 或di=n-1若CiAjB=0,Ci是輸出矩陣C的第i行行向量。

對F,G解耦系統,其中一個解可定義如下:

F=-B*-1A*

G=B*-1

(6)

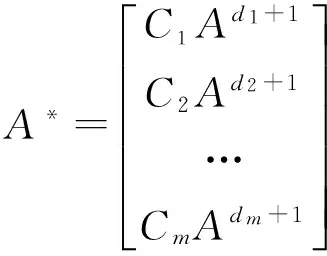
由式(4)—式(6)得到:

d1=d2=0

則原系統變為:

Y*=U′

(7)

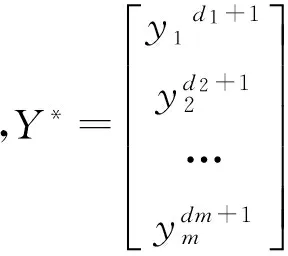
di+1為相關系數

在此三相永磁同步電機中可得:

(8)

由圖2 和式(8)得到三相永磁同步電機等效解耦系統如圖3所示。

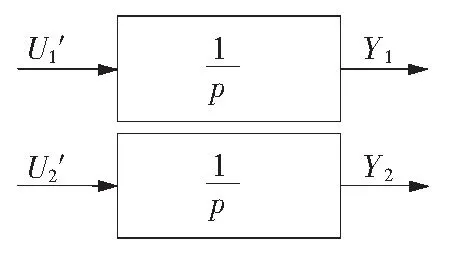
圖3 三相永磁同步電機等效解耦系統

Fig.3 Equivalent decoupling system of three phases PMSM

通常情況下,{F,G}解耦定義為:

(9)

由式(4)及式(9)可求得:

Q1(F)、Q2(F)的秩均是1,滿足條件,且B*是非奇異矩陣,滿足{F,G}能對原系統實現解耦的條件。

由于{F,G}解集不唯一,那么必然在F中存在自由因子,可以用來滿足設計需求,如可以任意設定閉環系統的極點。任意設定的極點個數p定義為

(10)

其中一個特定的解可定義為

(11)

G=B*-1

k=0,1…δ；δ=maxdi；i=1,2…m

由式(10)和(11)得到的矩陣F,G和p的個數如下:

(12)

則系統的傳遞函數

三相永磁同步電機轉換成一個穩定的解耦系統為

3 雙定子永磁同步電動機的動態模型

經過Park和Clarke坐標變換,基于d1d2q1q2軸的永磁同步電機模型為

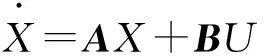
(13)

在此A、B矩陣對應定義為:

式中:Rs、L和Lm分別為電阻、自感和互感。

4 狀態反饋控制解耦方法在雙定子永磁同步電機中的應用

永磁同步電機耦合系統傳遞函數為

H=(sI-A)-1B

(14)

其中I是2×2單位矩陣,H是電機系統的傳遞函數。

設定期望中的對角化解耦系統Hdiag為:

為保持與原耦合系統相同的時間常數,定義τ=L/Rs

推導得F,G為:

應用狀態反饋解耦控制,系統變為:

此傳遞函數實現了電流輸出由對應電流輸入對應控制,實現了雙定子電機的解耦。

5 實驗仿真

實驗基于Matlab-simulink平臺下雙定子永磁同步電機的仿真,電機實驗參數為:Rs=17.5 Ω,L=53 mH,Lm=26 mH,兩定子夾角Υ=π/6, 轉速ω=100π rad/s。電流初始數值均為零,在不同時刻因負載的改變而改變其電流值。電流變換參數如表1所示。

表1 仿真電流變化參數表

反饋控制解耦方法的雙定子永磁同步電機的仿真結果如圖4所示。

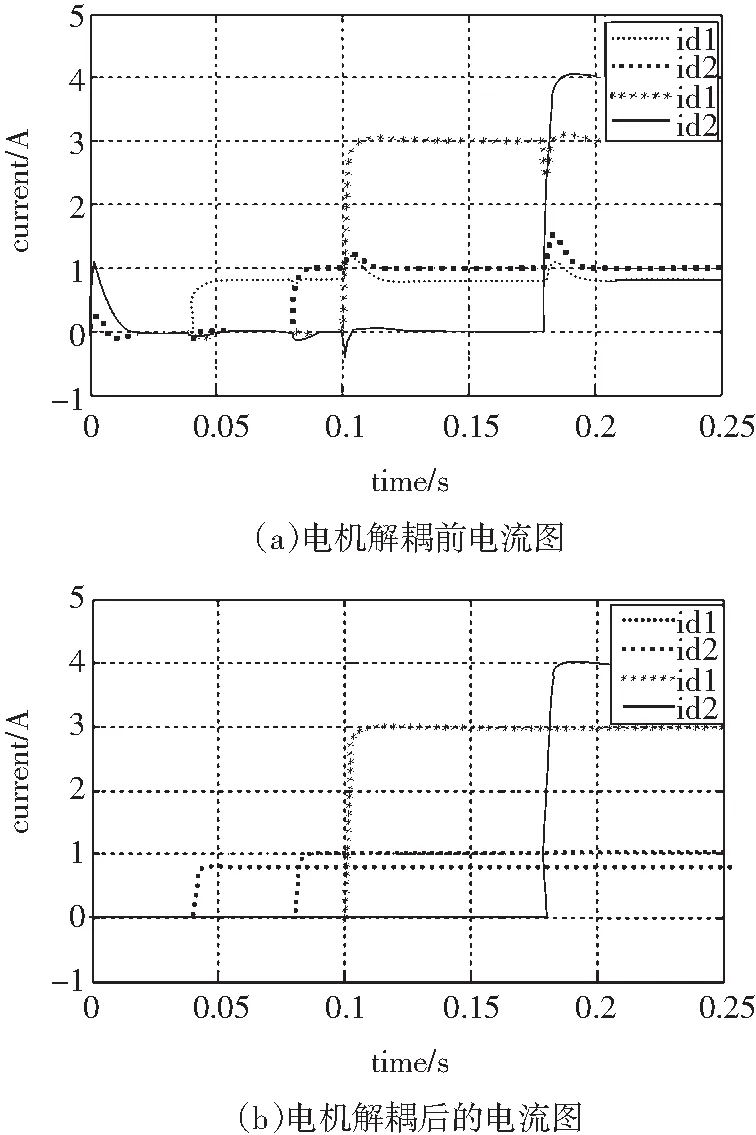
圖4 雙定子永磁同步電機的仿真結果

Fig.4 Simulation results of double stator permanent on magnet synchronous motor

從圖4解耦前后可知,解耦前,任一項電流的變化都會影響另外三項電流的數值,影響時間約0.02 s, 解耦后,任一項電流的變化都不會影響另外三項電流的數值。狀態控制解耦方法有效地解決了耦合問題。

6 結 語

由上述分析和實驗結果得知,狀態解耦控制有效解決了感應電機的非線性、強耦合問題，并使得四階的雙定子永磁同步耦合電機轉變為一階解耦系統。應用此方法不需要計算對于干擾非常敏感的電流微分分量。狀態解耦控制方法的應用范圍比前置解偶矩陣廣泛,可以通過任意設定極點位置而建立不同響應時間常數下的系統模型,靈活性高,且不受對象耦合矩陣是否為非奇異矩陣的約束。并且在工程上有效解決了耦合問題。

[1] 王鑫,李偉力,程樹康. 永磁同步電動機發展展望[J]. 微電機. 2007(05): 69-72. WANG Xin, LI Weili, CHENG Shukang. Development and prospect of permanent magnet synchronous motor [J]. Micromotors, 2007(05): 69-72.

[2] 黃偉忠,宋春華. 永磁交流伺服電機國內外市場概況[J]. 微特電機. 2009, 37(1): 59-62. HUANG Weizhong, SONG Chunhua. Summary of domestic and international market of permanent magnet AC servo motor [J]. Small & Special Electrical Machines, 2009, 37(1): 59-62.

[3] DURAN M J, KOURO S, WU B, et al. Six-phase PMSG wind energy conversion system based on medium-voltage multilevel converter[Z]. IEEE, 2011-10.

[4] YIFAN ZHAO and LIPO T A. Space vector PWM control of dual three-phase induction machine using vector space decomposit-ion[J]. IEEE Transactions on Industry Applications. 1995, 31(5): 1100-1109.

[5] ANDRIOLLO M, BETTANINI G, MARTINELLI G, et al. Analysis of Double-star permanent-magnet synchronous generators by a general decoupledd-qmodel[J]. IEEE Transactions on Industry Applications. 2009, 45(4): 1416-1424.

[6] 范鄒. 三相電壓型PWM變流器的線性化狀態反饋解耦控制[J]. 通信電源技術. 2008，25(1)：0032-0035. FAN Zou. Linear state feedback decoupled control for three-phase voltage source PWM converter [J]. Telecom Power Technologies, 2008，25(1)：0032-0035.

[7] 董英,宋文祥,尹赟,等. 基于內模控制的三電平PWM整流器控制方法[J]. 電氣傳動. 2012(02): 44-47. DONG Ying, SONG Wenxiang, YIN Yun, et al. Control strategy of level PWM rectifier based on internal model control [J]. Electric Drive, 2012(02): 44-47.

[8] 達成莉. 多變量系統解耦現狀的分析[J]. 工業控制計算機. 2011, 24(12): 69-71. DA Chengli. Current situation and development of decoupling control on MIMO system [J]. Industrial Control Computer, 2011, 24(12): 69-71.

[9] BENKHORIS M F, TALI-MAAMAR N, TERRIEN F. Decoupling algorithm in view of multivariable electrical drives cont-rol[Z]. 2002: 6, 4861-4866.

[10] 鐘天云,毛潔,周揚忠. 基于逆系統解耦永磁同步電動機直接轉矩控制[J].福州大學學報:自然科學版.2014(2):258-264. ZHONG Tianyun, MAO Jie, ZHOU Yangzhong. DTC for permanent magnet synchronous motors based on inverse decoupling control [D]. Journal of Fuzhou University: Natural Science Edition, 2014(2): 258-264.

[11] 周志剛. 一種感應電機的解耦控制方法[J]. 中國電機工程學報. 2003, 23(2): 121-125. ZHOU Zhigang. A induction motor de-couple control method [J]. Proceedings of the CSEE, 2003, 23(2): 121-125.

[12] PARASKEVOPOULOS P N, KOUMBOULIS F N, KOUVAKAS N D, et al. I/O decoupling via dynamic controllers-a state space approach[C]. Limassol: 2005.

[13] 楊明,付博,李釗,等. 永磁同步電動機矢量控制電壓解耦控制研究[J]. 電氣傳動. 2010(05): 24-28. YANG Ming, FU Bo, LI Zhao, et al. Research on voltage decoupling control of vector control for permanent magnet synchronous motor [J]. Electric Drive, 2010(05): 24-28.

[14] 梅國權. 永磁同步電機矢量控制系統的研究與設計[D]. 南京理工大學, 2013. MEI Guoquan. Research and design of vector control system of PMSM [D]. Nanjing University of Science and Technology, 2013.

(責任編輯 郭金光)

Research on state variables feedback decoupling technique for permanent magnet synchronous motor

YANG Gui, PENG Xiangang

(School of Automation, Guangdong University of Technology, Guangzhou 510006, China)

Aiming at the permanent magnet synchronous machine (PMSM) coupling, this paper establishes its nonlinear mathematical model based ond-qaxis after the Park and Clarke transformation. The principle of state variables feedback decoupling technique is applied to realize decoupling control of PMSM phase current and voltage. The simulation results indicate that the technique sloves the coupling problem with the effectiveness which is verified statical and dynamical, flexible and conveninet.

permanent magnet synchronous machine, decoupling, feedback control

2015-01-22。

廣東省自然科學基金(10151009001000045)。

楊 貴(1989—),女，在讀碩士研究生,從事電機系統建模與控制研究工作。

TM341

A

2095-6843(2015)04-0326-05