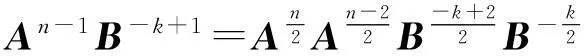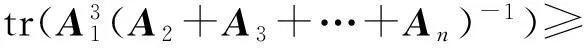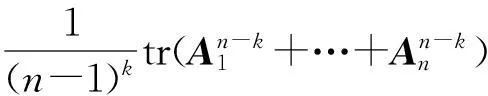一類矩陣跡的不等式
周其生,金樂樂
(安慶師范學院 數學與計算科學學院,安徽 安慶 246133)
?
一類矩陣跡的不等式
周其生,金樂樂
(安慶師范學院 數學與計算科學學院,安徽 安慶 246133)
摘要:本文利用Young不等式和Lieb-Thirring不等式,給出一類矩陣跡的新的不等式,且推廣了一些文獻的結果。
關鍵詞:矩陣;跡;不等式
矩陣的跡是矩陣的一個重要數值特征,由于矩陣跡的運算在數值計算、逼近論以及統計估計、隨機控制、濾波和經濟計量學等理論中應用廣泛,因此,對于它的討論引起眾多數學工作者的重視。由于矩陣的乘法無實數乘法所具有的交換性,這使得許多關于實數的不等式不能直接推廣到矩陣論中,一些看似平常的代數不等式,推廣為按L?wner偏序的矩陣不等式一般可能不成立。由于矩陣跡運算克服了矩陣乘法交換性的困難,又使得實數不等式的推廣成為可能,鑒于矩陣乘積的跡一般不等于矩陣跡的乘積,故而又成為推廣的障礙,因此,研究矩陣不等式不僅具有應用價值,而且也極具挑戰性。本文將利用矩陣跡的Young不等式和Lieb-Thirring不等式,以及關于跡的性質,將一些熟知的實數不等式推廣到矩陣論中,得到關于矩陣跡的不等式。
楊晉和稽國平、湯正誼等人分別在文[1]和[2]中給出如下一些實數不等式。
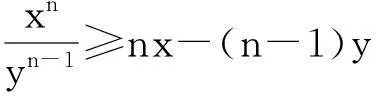
2.設a,b,c為正數,則
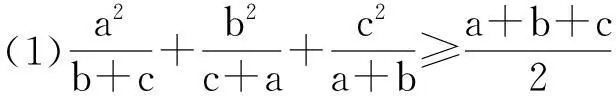

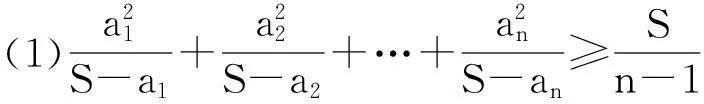
本文將以上實數不等式推廣為矩陣跡的相應不等式,并做了更深入的討論。為此,先給出兩個重要引理。
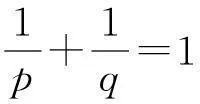

特別,當A,B為同階半正定Hermite矩陣時,有
等號成立當且僅當B=Ap-1。
引理2[4](Lieb-Thirring不等式)設A,B為同階半正定Hermite矩陣,n為任意正整數,則
tr(AB)n≤tr(AnBn)
等號成立當且僅當n=1或AB=BA。
關于矩陣跡的性質可參閱文獻[5-6]。下面給出本文的主要工作。
定理1設A,B為半正定Hermite矩陣,n為任意正整數,則有
ntr(An-1B)≤(n-1)trAn+trBn
(1)
等號成立當且僅當B=A。
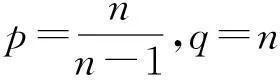

定理1是Jacobsthal不等式的推廣,當n=2時就是AG不等式。將它變形,即
定理2設A,B為半正定Hermite矩陣,B可逆,n為任意正整數,則有
tr(AnB-(n-1))≥ntrA-(n-1)trB
(2)
等號成立當且僅當n=1或者A=B。
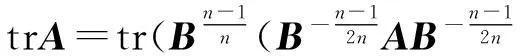

因此,(2)式成立。
推論1設A,B,C是半正定Hermite矩陣,且任兩個的和為可逆陣,則有
tr[A2(B+C)-1+B2(C+A)-1+C2(A+B)-1]≥
(3)
tr[A2(A+B)-1+B2(B+C)-1+C2(C+A)-1]≥
(4)
當且僅當A=B=C時等號成立。
證明由定理2并以2A,2B,2C分別代替A,B,C得
tr[(2A)2(B+C)-1]≥4trA-tr(B+C)
tr[(2B)2(A+C)-1]≥4trB-tr(A+C)
tr[(2C)2(A+B)-1]≥4trC-tr(A+B)
三不等式相加得
4tr[A2(B+C)-1+B2(C+A)-1+C2(A+B)-1]≥
2tr(A+B+C)
所以(3)式成立。再由定理2知,(3)式等號成立當且僅當2A=B+C,2B=A+C,2C=A+B,即A=B=C。同理可證(4)式及等號成立條件。
注1(3)式不能改成如下形式的推廣:

tr[A2(B+C)-1+B2(A+C)-1+C2(A+B)-1]≥
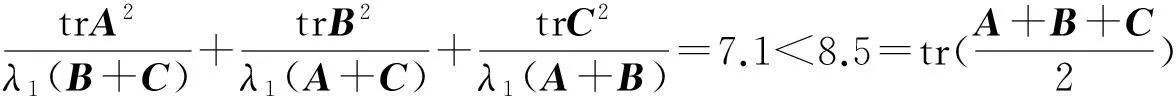
進一步,有下面更一般結果。
定理3設A1,A2,…,An(n>1)為同階半正定Hermite矩陣,任意n-1個之和可逆,則
(5)
(6)
等號成立當且僅當A1=A2=…=An。
證明為得到不等式左邊矩陣商和式的跡的最佳下界,在上面已證不等式tr(A2B-1)≥2trA-trB中以αΑ代A(α為正數)得
α2tr[A2B-1]≥2αtrA-trB
(7)
在(7)式中分別以A1,…,An代A,以A2+…+An,…,A1+…+An-1代B得
……
將上面各不等式相加得


(5)式等號成立當且僅當αA1=A2+…+An,…,αAn=A1+…+An-1,當且僅當α=n-1,A1=A2=…=An。同理可證(6)式及等號成立的條件。
定理4設A1,A2,…,An(n>1)為同階半正定Hermite矩陣,任意n-1個之和可逆,則
(8)
(9)
證明由定理2并以αA1(α為正數)代替A,再以A2+…+An代替B得
同理可得另外n-1個不等式,將這n個不等式相加得

為了繼續推廣上面的結果,先給出類似于定理2的一個結論。
定理5設A,B為同階半正定Hermite陣,B可逆,則對任意自然數k,n(k tr(AnB-k)≥2tr(An-1B-k+1)-tr(An-2B-k+2) (10) 從而有(10)式成立。 定理6設A1,A2,…,An(n>1)為同階半正定Hermite矩陣,任意n-1個之和可逆,則 (11) (12) 下面進一步研究k次冪的商和式的跡,有如下結果, 定理7設A1,A2,…,An(n>1)為同階半正定Hermite矩陣,任意n-1個之和可逆,k≥2為正整數,則 (13) (14) 證明仿照定理6的證明可得 再由Young不等式得 j=2,3,…,n 代入上式得 相仿地可得其余n-1個不等式。把這n個不等式相加,化簡得 顯然當α=n-1時,得到最佳結果(13)式。同樣可證(14)式。 定理8設A1,A2,…,An(n>1)為同階半正定Hermite矩陣,任意n-1個之和可逆,則對任意自然數n,有 (15) (16) 證明記S=A1+A2+…+An,由定理4并仿照定理6的證明,可得 將各式相加得 由定理7可得 代入上式得 取最佳常數α=n-1時,即知此時(15)式成立。同理可得(16)式。 注2通過以上討論,猜想,對同階半正定Hermite矩陣A1,A2,…,An(n>1),任意n-1個之和可逆,則對任意自然數k,n(k 當k=1,2,n-1時,分別是定理7(令k=n),定理8和定理4的結果。 參考文獻: [1]楊晉.一個不等式變形的應用[J].中學數學月刊,1999,12:44-46. [2]稽國平,湯正誼.兩個優美而有用的不等式[J].中學數學月刊,2000,6:24-27. [3]T.Ando.Matrix young inequlities[J].Oper.Theory Adv.Appl.,1995,75:33-38. [4]R.Bhatia.Matrix analysis[M].New York:Spring-Verlag,1997:289-317. [5]X.Zhan.Matrix inequalities[M].Berlin:Springer-Verlag,2002:35-38. [6]王松桂,吳密霞,賈忠貞,等.矩陣不等式[M].北京:科學出版社,2006. Inequality on Trace of a Class of Matrix ZHOU Qi-sheng, JIN Le-le (School of Mathematics and Computation Science,Anqing Teachers College,Anqing 246133,China) Abstract:In this paper, inequality on trace of a class of matrix are provided, by using Young inequality and Lieb-Thirring inequality, and the result of some of the literature is generalized. Key words:matrix, trace, inequality 文章編號:1007-4260(2015)03-0001-04 中圖分類號:O178,O151.21 文獻標識碼:A DOI:10.13757/j.cnki.cn34-1150/n.2015.03.001 作者簡介:周其生,男,安徽金寨人,安慶師范學院數學與計算科學學院教授,主要研究方向為算子理論。 基金項目:安徽省教育廳自然科學項目(2013Z186)。 收稿日期:2014-11-25 網絡出版時間:2015-8-25 15:40網絡出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.001.html