雙定子單轉子旋轉型行波超聲電動機轉子的優化設計

紀躍波，王 濤

(集美大學，廈門361021)

0 引 言

超聲電動機是一種新型電機，其原理是利用壓電陶瓷的逆壓電效應，通過激勵電壓的作用使定子產生振動，之后再通過定轉子間的摩擦力，實現電能到機械能的轉換，使轉子產生定向的轉動。與傳統電機相比，它具有結構簡單、低速大轉矩、響應速度快、不受磁場干擾等優點。在工業控制、轎車電器、計算機、智能機器人和航空航天領域有著廣泛的應用前景［1-2］。

由于超聲波電動機的特殊結構和運行機理，使得超聲波電動機具有不同于傳統電磁型電機的優點，但也有效率低輸出功率小的缺點。造成這些缺點的主要原因是定、轉子在相互作用時其接觸面積過小，這使得彈性體中的振動能利用率不高，限制了電機的輸出能力;因而有效增大定轉子接觸面積對于提高超聲電動機效率是非常必要的。一般來說，改變定子和轉子的結構可以達到以上的目的，國內外學者針對定子的設計進行了研究，并取得了一定的成果［3-6］;對于轉子的設計，一般都提高它的柔性，徐志科［7］用軟件ANSYS 建立定轉子二維接觸模型，比較了剛、柔性轉子情況下接觸面上的應力分布，仿真結果表明柔性轉子具有更好的接觸范圍;蔣春容［8］提出了U 型柔性轉子，通過仿真證明，電機在轉速和轉矩上都有明顯提升，原因是采用U 型轉子時接觸面積更大;王光慶［9］同樣提出了柔性轉子的設計。

針對轉子的設計，本文利用有限元分析軟件ANSYS，基于本實驗室研發的雙定子單轉子旋轉型超聲電動機，建立定轉子二維靜力學和三維動力學接觸模型，得到剛、柔性轉子的輸出性能，通過對比得出相關結論，為雙定子單轉子旋轉型超聲電動機的設計和分析提供了理論依據。

1 雙定子單轉子旋轉型超聲電動機

雙定子單轉子旋轉型超聲電動機［10］采用結構完全相同的兩個定子對稱布置，并且軸向壓緊轉子兩個端面，由壓簧提供預壓力，通過與中間轉子相連的轉軸輸出機械能。其結構如圖1 所示。

雙定子單轉子旋轉型超聲電動機保證兩個定子的工作面均勻，這樣可以克服傳統旋轉型行波超聲電動機定、轉子間存在徑向接觸不均勻、接觸范圍小等缺陷，有望提高電機的轉速，輸出轉矩和效率，具有廣闊的應用前景和積極的現實意義。

圖1 雙定子單轉子超聲電動機結構

2 定子運動方程及表面質點的運動［1］

根據Kirchhoff 薄板理論，在柱坐標系(r，θ，z)下，定子中性面的形變可用下式表示:

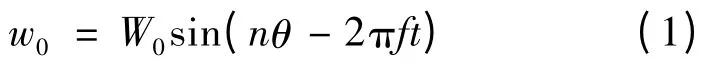
式中:W0為行波的振幅;n 為定子產生行波圓周上的波數;θ 為電機周向坐標;f 為外加電壓的頻率。由于定子表面的法向形變與中性層的法向形變相同，則定子表面質點的法相位移w1可表示:

若行波的相位增加180°，則有下式:

表1 位移載荷中各項參數

3 電機轉子的設計

由電機結構圖可以看出，本實驗室研發的雙定子電機的預壓力是通過壓簧的變形后施加在腹板上，再到上定子的支撐板上，之后再由上定子齒作用到轉子上，實現定子——轉子——定子之間的接觸。由于預壓力的施加，會使定轉子間發生變形，在轉子是剛性的情況下，示意圖如圖2 所示。

圖2 預壓力作用下定轉子形變圖

由圖2 可以看到，當轉子是剛性時，定轉子接觸面積是有限的，基本上只在轉子內圈附近接觸，這不僅限制了電機的輸出性能，而且定轉子之間磨損很嚴重，縮短了電機的壽命。這就需要對轉子進行改進，在保證有足夠的機械強度的情況下，提高轉子的柔性，增加定轉子的有效接觸面積，使定子和轉子能夠平行接觸。本文設計的轉子結構如圖3 所示，該結構中主要通過圖示的柔性環節進行變形來調整轉子與定子的接觸配合。

圖3 轉子結構圖

4 電機轉子有限元分析

4.1 材料與結構參數的確立

本文分析的超聲電動機的定子是由磷青銅組成，其尺寸如圖4 所示。定子外半徑Ra=30 mm，內半徑ra=22.5 mm，高度ha=4.5 mm，中性層到定子上表面距離he=2.5 mm，齒高厚度ht=2 mm，支撐板長度wx，高度wy和厚度wz分別為0.5 mm，0.6 mm 和1 mm，基座內圈半徑r =9 mm，高度h0=2.5 mm，螺孔到中心距離r0=13 mm，半徑為2 mm。

圖4 定子截面圖

轉子采用柔性轉子，由硬鋁和摩擦材料組成，兩者進行黏貼，而且上下對稱，其尺寸如圖5 所示。外半徑R1=29.5 mm，內半徑R2=27.5 mm，厚度h =8 mm，h1=1 mm，h2=3 mm，b=19.85 mm;支撐板外半徑R3=12 mm，內半徑R4=4 mm，為了形成柔性轉子，bh=0.3 mm，hh=2 mm，摩擦層厚度h3=0.3 mm。

圖5 轉子截面圖

定、轉子材料參數如表2 所示。

表2 定、轉子材料的主要參數

4.2 二維靜力學分析

由于電機定轉子結構都是軸對稱的，所以對其截面分析即可，二維分析中采用PLANE42 單元，建立線線接觸模型，定義摩擦系數為0.15，并消除初始滲透;根據實際情況進行約束，對下定子內圈節點進行x 和y 約束，上定子及轉子的內圈節點只進行x方向的約束，在上定子支撐板節點上施加125 N 的預壓力。建立的接觸模型圖6(a)所示。

定、轉子形變情況如圖6(b)，在預壓力的作用下，定、轉子間發生了彈性變形，在上下接觸面上，轉子徑向的變形量與定子的變形量保持一致，這樣就保證了定、轉子之間在徑向有良好的接觸，從而提高了電機的性能。

圖6 柔性轉子定、轉子二維接觸模型

接觸面上的應力分布如圖7 所示，由圖7 可以看出，隨著接觸面上的位移的增加，應力由小增大，在大概26 mm 處達到最大值，上、下接觸面的最大應力分別為3.91 ×105N/m2，4.78 ×105N/m2，之后逐漸減小。

圖7 柔性轉子上接觸面與下接觸面的應力分布圖

為了展示柔性轉子的優勢，同樣對剛性轉子進行分析，剛性轉子與設計轉子具有相同的厚度及接觸半徑，按照前述方法建立接觸模型，其應力分布曲線如圖8 所示，可以看到，在預壓力的作用下，隨著接觸面上的位移的增加，應力逐漸減小，且其中應力的最大部分主要集中在轉子內圈與定子接觸區域，上、下接觸面的最大應力分別為1.56 ×106N/m2，1.28 ×106N/m2，這樣會使應力過大且分布過于集中，導致接觸面摩擦損耗大，大大縮短電機的壽命。

圖8 剛性轉子上接觸面與下接觸面的應力分布圖

對比兩種轉子的應力分布曲線可以知道，柔性轉子在接觸面上的最大接觸應力遠遠小于剛性轉子，且應力分布相對來說較平衡，這樣，既保證了定、轉子間的接觸面積，又減輕了摩擦層的磨損量，有利于提高電機的輸出性能。

4.3 三維動力學分析

三維模型中，磷青銅、硬鋁和摩擦層均采用ANSYS 單元庫中的三維實體單元SOILD 95。不考慮硬鋁與摩擦層粘結層的影響，為保證兩者之間的重合部分力和位移傳遞的連續性，在劃分網格前需將硬鋁和摩擦層進行粘結。網格劃分采用分割的方法，對計算精度貢獻較大部分的網格應細化。建立面面接觸模型，將定子上表面定義為目標面，與之接觸的摩擦層表面定義為接觸面。定義摩擦系數為0.15，并消除初始滲透。邊界條件的施加應盡量反映電機實際工作情況，施加如下:(1)對下定子三個螺孔節點進行全方位約束，以阻止下定子做平移運動或周向旋轉運動;(2)對上定子三個螺孔節點施加徑向位移約束，以阻止上定子做平移運動;(3)對轉子內圈節點施加徑向位移約束，軸向保持自由，使轉子不做平面平移運動;(4)分別在下定子中性面節點和上定子中性面節點施加式(2)和式(3)的位移載荷，使下定子做行波運動，而上定子做相位不斷變化的行波運動;(5)在上定子支撐板表面施加軸向預壓力F=125 N。柔性轉子接觸模型如圖9 所示。

圖9 有限元接觸模型

求解時間為30 μs;60 個子步，以使每一子步定、轉子變化量足夠小;并讀出每一子步結果。

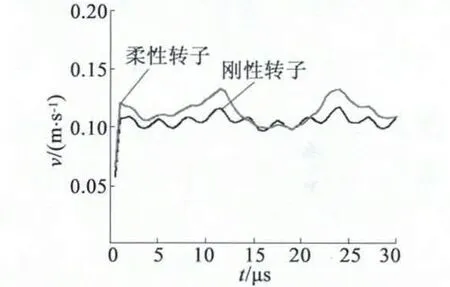
圖10 剛、柔性轉子質點速度對比

由圖10 可以看出，在預壓力為125 N 的作用下，柔性轉子和剛性轉子質點的速度在一定范圍內波動，平均值分別為0.12 m/s 和0.11 m/s。轉子的空載速度可以通過下式計算得到:

式中:vr為質點切向速度;Rm為轉子半徑;nr為轉子轉速。

圖11表示的是預壓力F=125N時的電機轉速-轉矩特性曲線。由圖11 可知，當轉子為剛性時，電機的空載轉速為36 r/min，堵轉力矩為0. 32 N·m;當轉子為柔性時，電機的空載轉速為39 r/min，堵轉力矩為0.36 N·m。因此，采用柔性轉子有利于提高電機的轉矩和轉速性能。

圖11 剛、柔性轉子電機的轉矩-轉速曲線比較

5 結 語

本文以雙定子單轉子旋轉超聲電動機為研究對象，針對其效率低的缺點，提出改進轉子的方案，對轉子進行柔性優化設計。通過建立二維靜力學和三維動力學接觸模型，分析了采用柔性轉子時，轉子接觸面的壓力分布及電機的轉矩-轉速特性;并在相同的情況下與剛性轉子進行比較，得到當采用柔性轉子時，電機性能及壽命均有提高的結論。仿真結果為雙定子單轉子旋轉型超聲電動機的設計和分析提供了理論依據。

［1］ 趙淳生.超聲電機技術與應用［M］.北京:科學出版社，2007.

［2］ 胡敏強，金龍，顧菊萍. 超聲電機原理與設計［M］. 北京:科出版社，2005.

［3］ 陳超，曾勁松，朱華，等.微型行波超聲電機定子的參數優化設計［J］.中國機械工程，2009，20(5):68 -72.

［4］ 王一鈞，胡夏夏，王志強.超聲波電機定子設計參數間交互作用對電機模態頻率的影響［J］.微電機，2010，43(5):48 -53.

［5］ 侯飛.壓電定子與壓電轉子振型嵌合式旋轉型行波超聲電機［D］.廈門:集美大學，2013:29 -35.

［6］ 胡百振，李有光，趙淳生，等.新型縱彎超聲電機振子的設計與分析［J］.壓電與聲光，2014，36(3):353 -356.

［7］ 徐志科. 行波型超聲波電機的模型仿真與試驗研究［D］. 南京:東南大學，2005:65 -70.

［8］ 蔣春容，胡敏強，金龍，等.中空環形行波超聲波電機有限元接觸模型［J］.東南大學學報，2014，44(1):99 -103.

［9］ 王光慶.行波型超聲電機的若干關鍵問題研究［D］. 杭州:浙江大學，2006:104 -106.

［10］ 尹育聰，姚志遠，趙淳生.行波型旋轉超聲電機兩種組合方式的實驗研究［J］.中國機械工程，2011，22(1):84 -87.