水平軸磁懸浮風力發電機混合磁軸承系統研究

張 晨，張 濤，倪 偉，王曉暉，莫麗紅，葉小婷，賈紅云

(1.淮陰工學院，淮安223003;2.南京信息工程大學，南京210044)

0 引 言

風力發電機(以下簡稱風力機)主軸系統的支承方式直接影響著風力機的起動阻力矩、發電風速、維護成本和使用壽命。為了根本消除機械摩擦磨損、減少后期維護、增加發電量和提高風能資源的利用范圍，國內外眾多學者將磁懸浮軸承技術應用到風力發電機中，又稱磁懸浮風力發電機。但大多數的研究，主要是永磁軸承［1-6］與機械軸承配合使用，完成風力機主軸系統的支承。由于永磁軸承一旦制作成型，承載力不能人為控制，在較大風速下，一旦主軸的偏移量過大，無法回到懸浮位置，機械摩擦磨損問題將再次出現。此外，永磁軸承多采用磁環疊加方式，磁環安裝精度要求高，通常占據的徑向(或軸向)空間也較大［2-6］。而混合磁軸承具有設計簡單、體積小、電功率消耗少等優點，很可能成為未來磁懸浮風力發電機的主要支承形式，并將在縮減磁軸承體積、減輕整機重量、提高結構緊湊程度和塔架安全性等［7］方面作出重要貢獻。因此，本文采用混合磁軸承作為風力機的徑向支承結構，在徑向偏移量接近為零時，不消耗電功率，單靠永磁力就能實現徑向二自由度穩定懸浮;在偏離懸浮位置時，又可以通過控制線圈中的電流，以應對徑向偏移量的變化。

本文首先介紹了徑向混合磁軸承的結構形式與數學模型，對風力發電機轉子受力情況進行了分析，并完成了徑向混合磁軸承結構參數設計與分析;然后，設計了其數字控制系統，構建了徑向混合磁軸承基礎實驗平臺，進行了轉子起浮、擾動等相關試驗。試驗結果表明，樣機參數設計合理，系統動、靜態性能良好，為小型磁懸浮風力發電機的研究奠定了良好的基礎。

1 結構形式與數學模型

圖1 是徑向混合磁軸承橫截面和軸向剖面圖，單箭頭為定子永磁體產生的偏置磁通，雙箭頭為線圈產生的控制磁通，兩者相互作用，將產生使轉子懸浮的徑向力F。

根據參考文獻［8 -9］，該磁軸承的等效磁路圖如圖2 所示。

圖2 徑向混合磁軸承等效磁路圖

假設轉子在x，y 軸上的偏移量分別為x，y，據磁路基爾霍夫定律，各氣隙處合成磁通:

根據轉子所受的電磁力與磁通關系得到:

將式(1)代入式(2)，采用泰勒展開式在平衡位置附近作線性化處理，然后再沿著x 和y 軸投影，并進行電流等效變換后，最終得到混合磁軸承徑向懸浮力數學模型的矩陣形式如下:

式中;且二者均為常數。

2 參數設計與分析

2.1 轉子受力分析

以一臺300 W 水平軸磁懸浮風力發電機的設計為例，在徑向混合磁軸承設計之初，必須要明確徑向懸浮力的大小，圖3 是轉子結構受力分析示意圖。

圖3 風力發電機轉子受力分析示意圖

根據徑向上的力平衡和B 點力矩平衡可得:

式中:G1是風輪裝置的重量，取114.3 N;G2是發電機轉子系統的重量，取24.5 N;N1是徑向懸浮力大小;N2是機械軸承的徑向載荷。

由式(4)計算得出:N1=178.57 N，N2=39.77 N。因此，混合磁軸承提供的徑向懸浮力為180 N。

2.2 設計結果

徑向混合磁軸承參數設計過程依次為氣隙長度選取、磁極面積估算、安匝數設計、永磁體和定子參數確定［10-11］。根據這些初步參數，利用ANSYS 仿真軟件，建立徑向混合磁軸承3D 模型，逐個對重要結構參數進行優化仿真，并分析磁場分布情況。最終，得到徑向混合磁軸承主要參數的設計結果，如表1 所示。

表1 徑向混合磁軸承設計要求和主要參數

2.3 磁軸承剛度

剛度曲線決定了磁軸承的線性工作范圍、懸浮力提升和振動調節時間。因此，分析徑向混合磁軸承的剛度特性是十分必要的。以混合磁軸承在徑向y 方向上的偏移量為例，研究磁軸承的剛度特性，并給出氣隙長度的大小。

圖4 是徑向混合磁軸承剛度曲線。從圖4(a)中可見，當徑向偏移量y 在0 ～0.35 mm 變化時，力-電流曲線(或電流剛度)近似呈線性關系;在y=0 mm，i=1 A 時，徑向懸浮力在180 N 左右，滿足徑向承載力設計要求。從圖4(b)中可以看出，在0 ≤y ≤0.3 mm 時，力-位移曲線(或位移剛度)呈線性增長，并隨著控制電流i 的增加，徑向懸浮力也是穩步提升;而在0.3 mm ＜y≤0.45 mm 時，曲線已不再是線性關系。綜合考慮，選擇氣隙長度為0.25 mm。這樣，既確保了磁軸承工作在線性范圍，徑向懸浮力的提升完全適應徑向偏移量的變化，轉子振動調節時間也能相應地減小。

3 數字控制系統設計

3.1 總體控制框圖

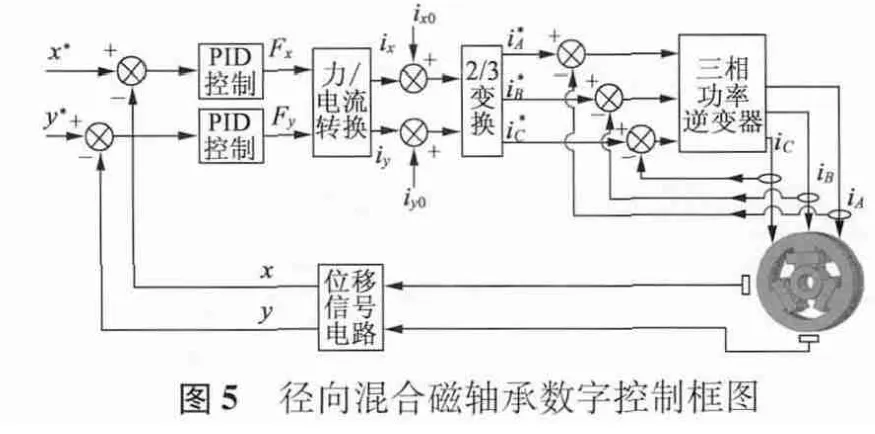
根據式(3)構建出徑向混合磁軸承數字控制框圖，如圖5 所示。首先，位移指令x*，y*與電渦流位移傳感器實時檢測到的x，y 比較后，經位移PID變換成Fx，Fy，由力/電流變換得到ix，iy，分別與ix0，iy0相加后，再由Clarke 逆變換得到i*A，i*B，i*C，與霍爾電流傳感器實時檢測的iA，iB，iC滯環比較產成PWM 波，驅動三相功率逆變器控制線圈A，B，C 中的電流，實現對x，y 方向上的徑向懸浮力控制。

3.2 主要硬件構成

本文采用的是以DSP 2812 開發平臺為核心的徑向混合磁軸承數字控制系統，其中硬件電路的設計主要包括DSP 控制電路、徑向功率驅動電路、位移/電流采樣電路和故障保護電路。

DSP 控制電路主要完成信號采集數字量、上位機PID 數據、位移-力-電流算法等內容，以產生PWM 輸出，驅動功率開關管，實現轉子徑向二自由度的穩定懸浮。徑向功率驅動電路采用的是交-直-交的主電路拓撲結構，經單相不控整流橋、電容濾波電路、光耦隔離電路和三菱IPM 智能模塊，提供磁軸承系統調節所需的能量。位移/電流采樣電路則是一個電壓調理的過程，以滿足DSP 的ADC 模塊模擬輸入0 ～3.3 V 的電壓限制。此外，為了避免IPM 智能模塊在電路發生故障時被損壞，同時考慮徑向混合磁軸承數字控制系統對電壓、電流的限定范圍。因此，需要設計過/欠電壓檢測、過電流檢測和驅動信號封鎖等故障保護電路。

3.3 程序流程圖

圖6 是徑向混合磁軸承數字控制系統的程序流程圖，主要包括主程序和主中斷服務程序。主程序是對系統控制寄存器，中斷PIE 和向量表以及EVA，ADC，SCI 等模塊進行了初始化設置;主中斷服務程序則是用來完成信號數字量轉換、位移-電流的雙閉環控制、上位機PID 調節參數的傳輸等任務。此外，還有SCIB 的接收、發送中斷程序。

圖6 程序流程圖

由于轉子起浮瞬間的徑向偏移量較大，容易引起頻繁振動，所以需要在PID 控制器中加入低通濾波環節，逐步衰減微分項幅度，也就是采用不完全微分PID 算法。這樣就使得微分作用時間變長，當轉子在平衡位置附近變化時很容易實現懸浮，減小了動態誤差，取得了較好的控制效果。

4 實驗結果與分析

根據表1 中徑向磁軸承設計參數，制作磁軸承樣機，并構建磁懸浮實驗平臺。采用數字PID 控制器進行徑向二自由度的位移控制，當比例增益Kp=10，積分時間常數Ti=0. 25，微分時間常數Td=0.000 010，微分增益ε =0.05 時，對位移接口電路進行調試，0 表示最大負位移，3 V 表示最大正便宜，1.5 V 表示轉子處于平衡位置，徑向混合磁軸承實現了穩定懸浮。圖7(a)是轉子起浮試驗，從圖7 中可以看出，起浮時間約40 ms，在y 方向上的起浮電壓大于1 V，x 方向小于1 V，穩定懸浮的電壓約為1.5 V;在斜向的方向上，給徑向轉子施加一個180 N 的外擾力，由圖7(b)可以看出，力的作用時間約為400 ms，x方向上的擾動較y方向明顯，在約20 ms的調節時間之后，轉子很快又回到了懸浮位置，說明系統具有較好的抗干擾能力。

5 結 語

本文主要研究了小型風力發電機用徑向混合磁軸承系統，包括結構形式、數學模型、參數設計、數字控制和懸浮實驗等方面的內容，解決了永磁軸承形式存在的懸浮力不可控、安裝精度高、占用空間大等問題，為混合磁軸承在小型風力發電機中的應用提供了實際參考，具有較高的科研價值和實踐意義。

［1］ 王念先，張錦光，胡業發，等.小型磁懸浮風力發電機起動阻力矩研究［J］. 武漢理工大學學報(信息與管理工程版)，2010，32(6):896 -899.

［2］ 李麗君，房建成，韓邦成，等.磁懸浮風力發電機用錐形被動磁軸承分析與設計［J］.軸承，2010，1:10 -13.

［3］ 田錄林，李言，田琦，等.徑向磁化的多環嵌套永磁軸承軸向磁力解析模型［J］.計算力學學報，2010，27(2):379 -383.

［4］ 李國坤，聞淑英，李珂.微摩擦力全永磁懸浮軸承在風力發電機中的應用［C］//2006 中國科協年會論文集(下冊)，2006.

［5］ 賈東方，汪希平，李文鵬，等. 基于ANSYS 的軸向磁化磁環位置特性的研究［J］.機械設計與制造，2010，(8):116 -118.

［6］ 田錄林，李鵬. 錐形永磁軸承磁力解析模型［J］. 中國機械工程，2014，25(3):327 -332.

［7］ 趙俊峰，朱熀秋. 磁懸浮風力發電機關鍵技術及其發展現狀［J］.微特電機，2013，41(11):71 -74.

［8］ 朱熀秋，沈玉祥，鄔清海，等.交流混合磁軸承建模與控制系統［J］.中國電機工程學報，2009，29(18):100 -105.

［9］ 張松，張維煜，朱熀秋.交流混合型磁軸承磁場及懸浮力特性分析［J］.微特電機，2012，40(2):11 -14.

［10］ 趙旭升，鄧智泉，汪波.異極性永磁偏置徑向磁軸承的參數設計與實現［J］.電工技術學報，2012，27(7):131 -138.

［11］ 張云鵬，劉淑琴，李紅偉，等. 基于磁路分析的軸向混合磁軸承徑向承載力解析計算［J］.電工技術學報，2012，27(5):137-142.