基于神經網絡的有限轉角力矩電動機滑模控制

許 輝，王自強

(北京航空航天大學，北京100191)

0 引 言

隨著電機設計技術的發展，需要具有各種不同工作形式的電機以滿足自動控制系統的要求，20 世紀70 年代起發展起來了一種新型電機——有限轉角力矩電動機(以下簡稱LATM)［1］，它與傳統電機的運動方式有所不同，能在有限轉角范圍內圍繞某一特定中心位置做周期性往復運動，從而提供了一種特殊的工作方式。有限轉角力矩電動機相比傳統的力矩電動機，具有結構簡單、輸出力矩大、可靠性高、波動小且易于控制等突出的優點。由這類電機構成的位置伺服系統頻帶寬、體積小、動態響應快，適用于掃描型紅外成像系統等高精度、高性能要求的控制系統。但由于有限轉角力矩電動機是多變量、非線性的復雜對象，而傳統的的PI 控制不能很好地控制它［2］，因而在此選擇滑模控制［13］來滿足其控制性能。滑模變結構控制廣泛應用于電機控制領域，可以應用在同步電機、異步電機以及直流電機中［3］。

滑模控制(以下簡稱SMC)對系統的精度要求不高，對外部擾動、內部參數攝動具有強魯棒性［4］，因而近年來成為許多學者青睞的控制方法，已經比較普遍用于永磁同步電動機［5］、直流電動機等系統中。國外對滑模變結構控制的研究時間比較早，研究的范圍也很廣，比如，既有對一般非線性系統的滑模控制［6］，也有針對的新型積分滑模控制同步電機的新型積分滑模控制［7］;為了能夠消除諧振、減少誤差，使RBF 神經網絡控制與滑模控制相結合，設計了基于RBF 網絡的滑模控制器［8-9］，很好地解決的存在的問題。近年來，國內也有很多用滑模控制來控制系統的論文，文獻［12］針對風電機組輸出功率的不穩定，對槳距角進行了RBF 神經網絡滑模控制，結果表明，該控制很好地提高了系統的魯棒性，也有效地減少了抖振現象。文獻［14］中，為了減少負載擾動對永磁同步電動機的影響，作者設計了負載轉矩滑模控制器，并用實驗方法驗證了系統的抗干擾能力。

本文結合滑模變結構控制和RBF 神經網絡控制來控制此系統，得到系統控制率，并用Lyapunov方法證明控制率的穩定性。最后進行了實驗研究和仿真分析［11］，結構表明控制方法能很好地提高系統的魯棒性，改善了系統的動態性能。

1 LATM 的數學模型

LATM 是近幾十年迅速發展起來的一種特種電動機，在跟蹤、紅外及激光成像等系統中獲得了廣泛的應用。LATM 在結構和運動形式上有別于一般的旋轉電機，它是在一定轉角范圍內作往復運動。這種電機具有良好的調節特性和機械特性，能直接驅動負載實現快速往復運動。

LATM 的磁場由永磁體建立，電機各個磁路的磁阻隨著轉子位置的改變而改變，其遵循“磁阻最小原理”，即磁通總是沿著磁阻最小的路徑閉合。LATM 采用直流電壓控制，電壓方程如下:

LATM 的轉矩方程:

LATM 的運動方程:

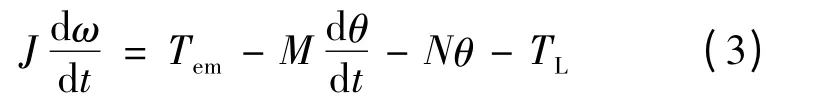
且:

式中:J 為轉動慣量;Tem為電磁轉矩;TL為負載轉矩;ω 為角速度;I 為電樞電流;M 為速度阻尼系數;N 為撓性樞軸扭轉剛度;k 為電路放大倍數;T 為電路延時時間常數;Kem為電磁轉矩系數。

對式(1)～式(4)做Laplace 變換，可得到電機模型:

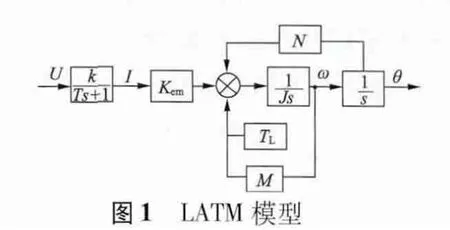
由式(1)～式(4)可得電機狀態矩陣:

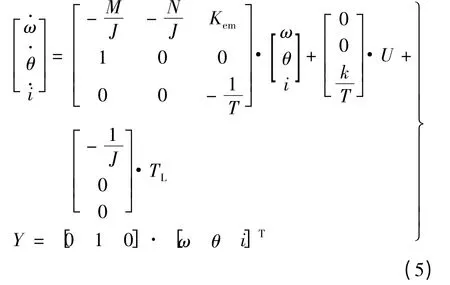
狀態方程也可寫:

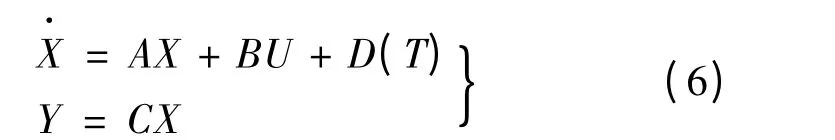
式中:D(T)為外界干擾，且滿足|D(T)|≤D。

2 控制策略

神經網絡是一種具有高度非線性的連續時間系統，它對非線性系統有很好的映射能力，并且有著強大的學習功能。在滑模變結構控制中添加神經網絡控制，可以實現自適應滑模控制。

2.1 RBF 神經網絡

Darken C 和Moody J 在20 世紀80 年代提出了RBF 神經網絡模型，它是具有單隱層的三層前饋網絡，圖2 為其結構圖。已經證明，RBF 網絡具有萬能逼近的性能［11］，因而可以很好地應用在非線性度高的電機上，比如本文中的有限轉角力矩電動機。

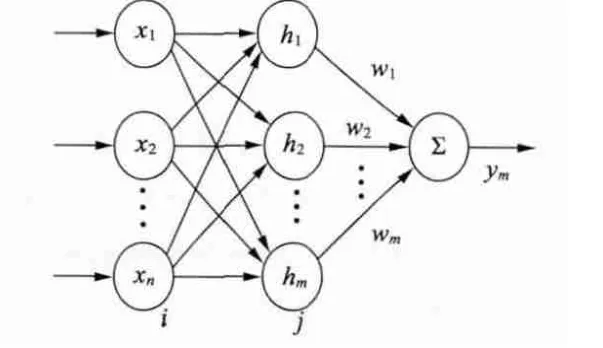
圖2 徑向基神經網絡結構圖

用RBF 神經網絡逼近函數f，則逼近算法:

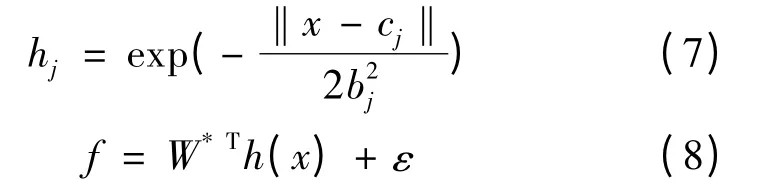
式中:x 為網絡輸入;j 為網絡隱含層第j 個節點;h =［hj］T為高斯函數;W*為網絡理想權值;ε 為網絡逼近誤差，且ε≤εN。

2.2 控制器設計

本節進行控制器的設計，定義角速度跟蹤誤差:

式中:X1d為理想跟蹤指令。

式(7)的微分:

設計滑模面:

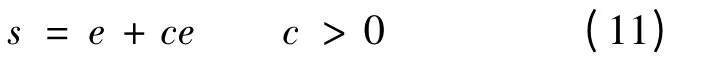
由以上各式可得:

則可設計控制律率:

式中:sgn(s)為符號函數;η 為學習效率，η ＞0。

由于參數J 是未知參數，所以我們采用RBF 神經網絡來逼近A(J)，以實現穩定控制。

RBF 神經網絡輸入取x=［e1e·1］T，則RBF 網絡輸出:

式中:h(x)為RBF 神經網絡的高斯函數。

將式(14)代入式(13)中，則控制率:

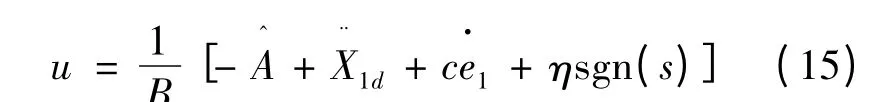
將式(15)代入式(12)中，得到:

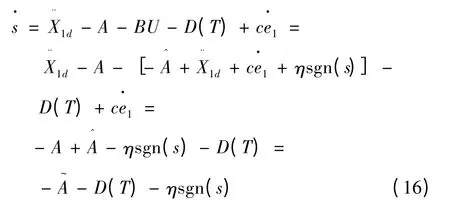
其中:

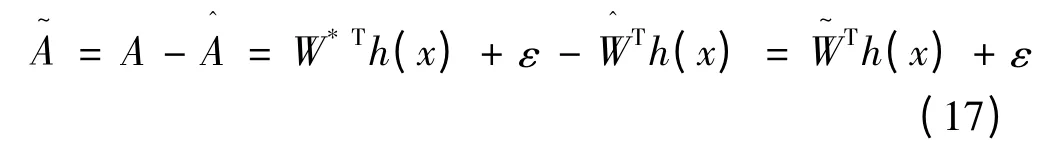
為了實現有限轉角力矩電動機的動力學系統的穩定控制，選取Lyapunov 函數:

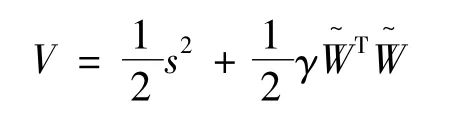
式中:γ ＞0。

對Lyapunov 函數求導，結合式(15)和式(16)，可以得到:

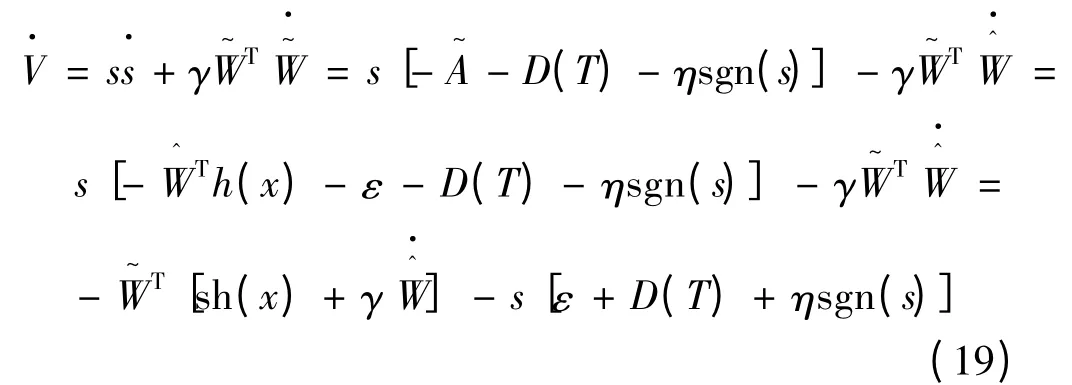
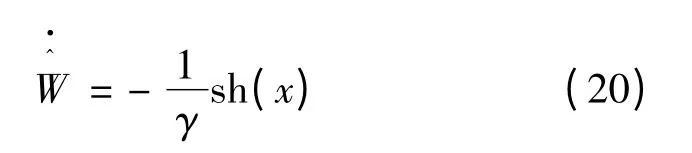
2.3 系統穩定性分析

對控制系統來說，穩定性是十分重要的。對一般系統而言，如果滿足滑模的存在及可達條件，則運動進入滑模動態區以后，就開始滑模運動，對通常的反饋系統而言，都希望滑模運動是漸進穩定的，下面就來證明本文中的控制方法是穩定的。

由式(19)與式(20)可知:

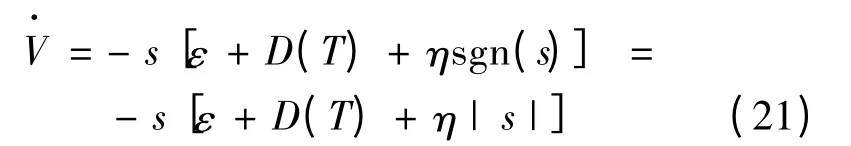
由于逼近誤差ε 可以限制得足夠小，取η≥εN+D，可得≤0，所以是負定的，此控制方法是穩定的。

3 仿真分析

為了驗證以上理論研究的準確性，下面對有限轉角力矩電動機控制系統進行了仿真研究。電機參數:速度阻尼系數M =3.88 ×10-5N·m·rad-1·s;撓性樞軸扭轉剛度N=0.028 9 N·m/rad;電路延時時間常數T =9.25 ×10-5s;電路放大倍數k =0.474;電磁轉矩系數Kem=0.032 N·m/A。

有限轉角力矩電動機的滑模控制系統結構圖如圖3 所示。

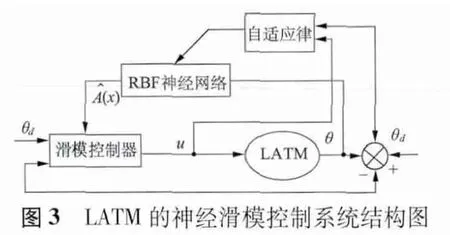
首先利用MATLAB/Simulink 建立仿真模型，電機模型由MATLAB/Simulink 中的元件以及電機的數學模型搭建，RBF 網絡及滑模控制器用MATLAB語言編程，M 函數實現。

本文采用兩種控制方法對比的方法來驗證所用算法的有效性。控制方法1 是傳統的PID 控制方法，控制方法2 是基于RBF 神經網絡的滑模控制方法。兩種控制器具有相同的誤差反饋增益。

為了著重突出本文中提出的基于RBF 神經網絡的滑模控制器的性能優點，分別設計了以下幾組仿真進行比較:

(1)為了比較系統的穩定性和快速性，在控制過程中，相同的時間點突然加入一個脈沖擾動，通過角度跟蹤誤差，比較傳統PID 控制器與神經網絡控制器的性能;

(2)為了比較傳統PID 控制器與神經網絡控制器的抖振性能，在控制仿真的整個過程中，加入相同的噪聲干擾，通過角度跟蹤誤差，來比較兩種控制方法的優劣。

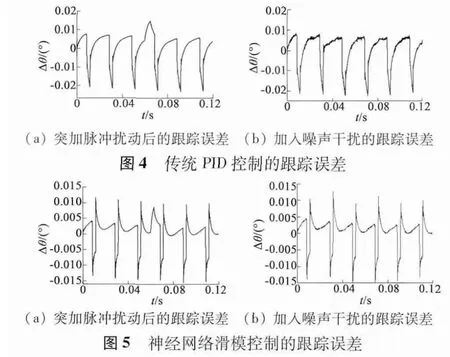
由圖4(a)與圖5(a)可以看出，在0.06 s 時加入一個脈沖干擾，圖4(a)中傳統PID 控制的系統的跟蹤誤差有一個明顯的增大，差不多經過一個周期才回歸正常，并且擾動峰值遠超出了正常時誤差峰值;而在圖5(a)中，由RBF 神經滑模控制的系統的跟蹤誤差雖有小幅增大，但很快趨于穩定，其擾動峰值也沒有超過正常時的誤差峰值。說明RBF 神經滑模控制具有更好的系統穩定性和快速性。由圖4(b)與圖5(b)的仿真圖可知，當仿真過程都加上噪聲干擾后，傳統PID 控制器的跟蹤誤差有0.023°，而基于RBF 神經網絡的滑模控制器的跟蹤誤差只有0.015°。在相同的工作狀態下，相對于傳統PID控制器，基于RBF 神經網絡的滑模控制器的跟蹤性能提升了34.8%。

4 實驗驗證

為了驗證神經網絡滑模控制器的優越性以及可行性，通過搭建控制實驗平臺進行實驗研究。有限轉角力矩電動機伺服系統主要包括有限轉角電機和控制器兩部分組成，如圖6 所示，控制器部分采用AD公司定點DSP中比較新的16位定點DSP，ADSP -2189。

圖6 實驗平臺

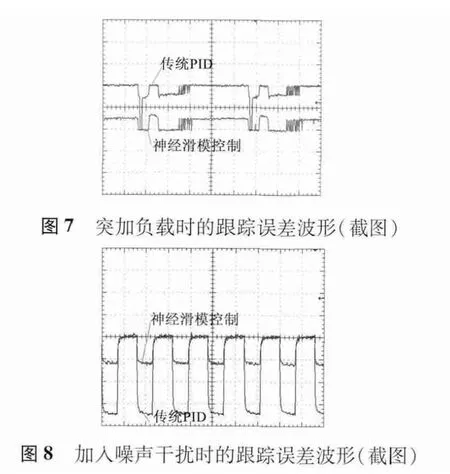
圖7 為突加脈沖擾動后的跟蹤誤差曲線。從圖7 中可以看出，用傳統PID 控制的跟蹤誤差曲線沿坐標軸向下方向有很明顯的脈動，而神經滑模控制的跟蹤誤差曲線則比較平緩，沒有較大脈動，這個結果與仿真結果基本一致。

圖8 為整個實驗過程加入噪聲干擾后的跟蹤誤差曲線。從圖8 可以看出，神經網絡滑模控制所產生的誤差遠遠小于傳統PID 控制所產生的誤差，誤差基本上減少了50%以上，這與前面的仿真結果一致。

從實驗部分可以看出，神經滑模控制器對于長時間工作在干擾環境下的電機，有很好的控制能力，大大增強了系統的魯棒性。

5 結 語

本文針對有限轉角力矩電動機系統存在的參數不確定性和非線性，建立了有限轉角力矩電動機的數學模型，提出了一種基于RBF 神經網絡的有限轉角力矩電動機滑模控制方法，對于控制系統存在的抖振現象，建立了其控制律，并采用李雅普諾夫理論證明了方法的收斂性。該方法克服了系統的非線性和對電機參數的依賴性，對負載擾動和電機參數擾動具有較強的魯棒性。理論分析和仿真分析均證明所提控制方案的有效性。最后通過實驗驗證了仿真結果的正確性，以及控制策略的可行性。從文中可以看出，神經滑模控制很適合控制長時間工作在干擾環境中的電機，能很好地提高系統的穩定性。

［1］ ZHANG Y，SMITH I R，KETTLWBOROUGH G.Performance evaluation for a limited-angle torque motor［J］. IEEE/ASME Transactions on Mechatronics，1999，14(3):335 -339.

［2］ DU Chun-yang，LI Tie-cai，CAO Zheng-cai.Accurate tracking control of a limited angel torque motor［J］. Electric machines and Power Systems，1999，27(11):1191 -1199.

［3］ UTKIN A，GULDNER J，SHI J X.Sliding mode control in electromechanical systems［M］.Oxon，UK:Taylor ＆ Francis，1999.

［4］ UTKIN V I. Variable structure systems with sliding modes［J］.IEEE Transactions on Automatic Control，1997，22(2):212-222.

［5］ 朱家廳，王莉娜，薛飛.永磁同步電機的滑模PI 模糊邏輯控制［J］.電氣傳動，2013，43(7):43 -48.

［6］ BOLIVARD M R，ZINOBER A S I，SIRA-RAMIREZ H.Dynamical adaptive sliding mode output tracking control of a class of nonlinear systems［J］. International Journal of Robust and Nonlinear Control，1997，7(4):387 -405.性積分滑模控制［J］.北京航空航天大學學報，2014，40(3):321 -326.

［7］ LIN F J，CHIU S L，SHYU K K. Novel sliding mode controller for synchronous motor drive［J］. IEEE Transactions on Aerospace and Electronic Systems，1998，34(2):532 -542.

［8］ HUANG S J，HUANG K S，CHIOU K C. Development and application of a novel radial basis function sliding mode controller［J］.Mechatronics，2003，13(4):313 -329.

［9］ LIN S C，CHEN Y Y. RBF network based sliding mode control［C］//IEEE International Conference on Systems，Man，and Cybernetics，1994:1957 -1961.

［10］ 韓松杉，焦宗夏，汪成文，等. 基于神經網絡的電液轉臺非線

［11］ 劉金琨.滑模變結構控制MATLAB 仿真［M］.北京:清華大學出版社，2005:188 -235.

［12］ 秦斌，周浩，杜康，等.基于RBF 網絡的風電記住變槳距滑模控制［J］.電工技術學報，2013，28(5):37 -41.

［13］ 付子義，李華群，王振鋒.基于神經網絡推力觀測器的永磁直線電機滑模控制［J］.電氣傳動，2009，39(11):48 -51.

［14］ 張曉光，孫力，趙克.基于負載轉矩滑模觀測的永磁同步電機滑模控制［J］.中國電機工程學報，2012，32(3):111 -116.