無刷直流電動機不同PWM 調制方式研究

姚緒梁，張 燕，江曉明，常英健

(哈爾濱工程大學，哈爾濱150001)

0 引 言

無刷直流電動機輸出轉矩大、調速控制方便、動態響應迅速、可靠性高，因此應用越來越廣泛［1-2］。但是它的轉矩脈動問題限制了其進一步發展。此外，轉矩脈動是電機產生振動與噪聲的重要原因。因此，分析研究無刷直流電動機的轉矩脈動具有重要意義。

文獻［3］指出換相過程中由于關斷相電流下降速率與導通相電流上升速率不一致，存在換相轉矩脈動，但脈沖寬度調制(以下簡稱PWM)的影響未考慮。文獻［4 -6］分析了PWM 調制方式對無刷直流電動機換相轉矩脈動的影響，并未從原理上進行分析，且還應考慮換相過程中關斷相與導通相電流變化率不一致的問題。

本文從非換相與換相過程出發，考慮了換相中關斷相電流下降速率與導通相電流上升速率不一致，并在此前提下，詳細分析了5 種不同PWM 調制方式下的轉矩脈動，通過仿真研究及原理分析，驗證了理論推導的正確性。

1 無刷直流電動機數學模型

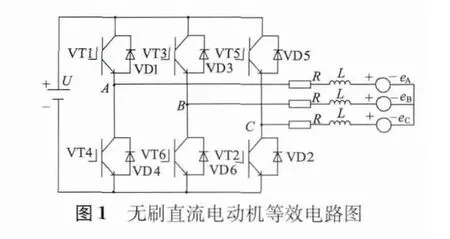
以三相六狀態兩兩工作方式為例，無刷直流電動機運行時，每個狀態有60°電角度，存在非換相與換相運行過程［7］。其等效電路如圖1 所示，三相端電壓方程:

式中:UA，UB，UC為定子各相繞組電壓;iA，iB，iC為定子各相繞組電流;eA，eB，eC為定子各相繞組反電勢;L，R 為定子各相繞組等效電感、電阻;Un為中性點對地電壓。

由電機理論得電磁轉矩方程:

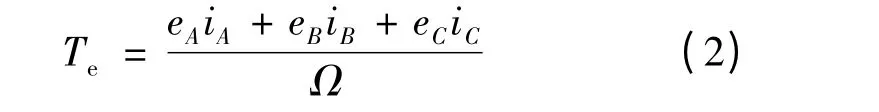
式中:Te為電磁轉矩;Ω 為機械角速度。

電機運行在三相六狀態兩兩工作方式下，HONLPWM(上橋臂恒通，下橋臂PWM)，HPWM - LON(上橋臂PWM，下橋臂恒通)，ON -PWM(前60°恒通，后60°PWM)，PWM -ON(前60°PWM，后60°恒通)及HPWM-LPWM(上下橋臂均PWM)為5 種常用的PWM 調制方式［8-9］，其中前4 種稱為單斬方式，后一種稱為雙斬方式。

2 非換相過程轉矩脈動

在非換相運行過程，定子繞組兩相導通，只有兩相中有電流。由于PWM 調制的影響，相電流存在持續波動［10］。以AB 相繞組導通為例，分析A 相電流。在一個PWM 周期T 內，設在t0～t1區間，PWM調制導通，S=1，相電流從I1增加到I2;在t1～t2區間，PWM 調制關斷，S =0，相電流從I2減小到I1。其中T =t2-t0為PWM 開關周期，S 為開關量。S可用D 來表示，D 為PWM 占空比。

5 種方式在開關管調制導通時電流回路一致，均為VT1，VT6 導通，區別在于調制關斷時續流回路不一致。由于4 種單斬方式開關管調制關斷時均為開關管與二極管導通，其過程等效，故只需分析一種，以HON -LPWM 方式為例;而雙斬方式為兩個二極管導通，需單獨討論。

2.1 HON-LPWM 調制方式

VT1 管進行PWM 調制，VT6 管恒通。VT1 管調制關斷時VD4，VT6 導通。端電壓方程:

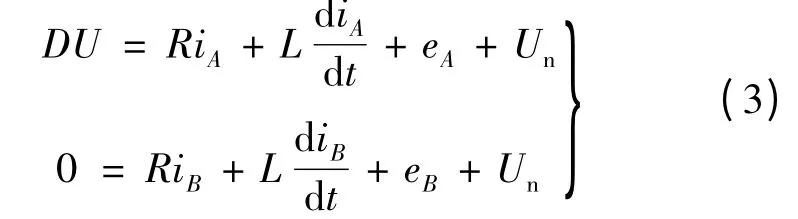
eA= -eB=E，iA+iB=0，忽略電阻R，由式(3)得:

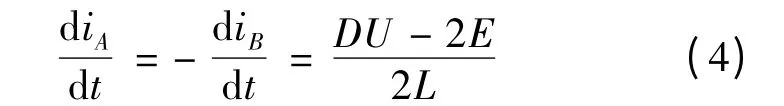
從而:

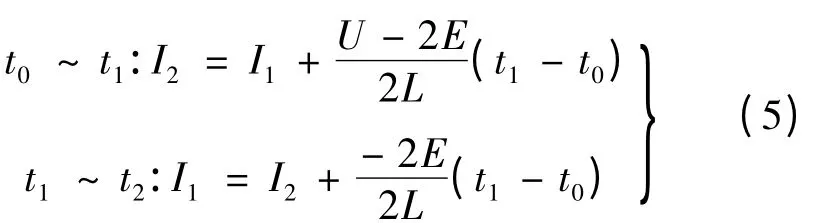
電流波動:

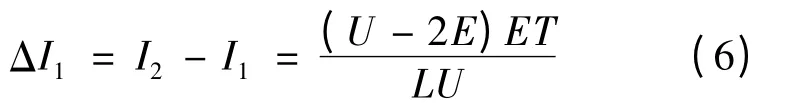
所以非換相過程單斬方式下電磁轉矩脈動:

2.2 HPWM-LPWM 調制方式

VT1 管，VT6 管均PWM 調制。VT1 管，VT6 管調制關斷時VD3，VD4 導通。端電壓方程:

同理解得電流波動:

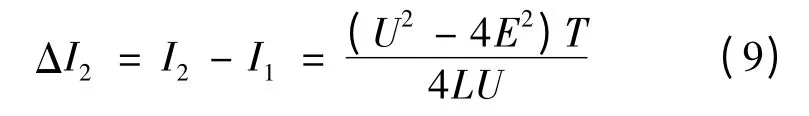
所以非換相過程雙斬方式下電磁轉矩脈動:

由式(7)和式(10)比較單斬和雙斬方式下非換相過程電磁轉矩脈動:

由于單斬方式的開關管調制關斷時開關管與二極管導通續流，與二極管相連的定子繞組中的電感作為儲能元件放電;而雙斬方式的兩個二極管導通，與之相連的兩個定子繞組中的電感作為儲能元件同時放電，直流電源吸收能量，使得其放電更快，電流下降更快，電流波動更大，轉矩脈動因此更大。與上述推導結論一致。所以，在非換相過程，單斬方式較雙斬方式有較小的轉矩脈動。

3 換相過程轉矩脈動

不同PWM 方式在上、下橋臂換相時續流回路不同，產生的轉矩脈動也不同，分為上、下橋臂換相討論。雙斬方式需單獨考慮［11-12］。

換相前的穩態轉矩:

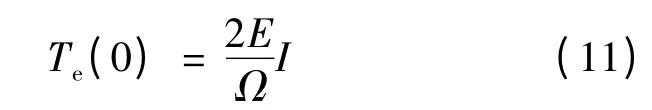
3.1 上橋臂換相

以AC 相換相到BC 相為例，電流的轉換通過關斷VT1，導通VT3 完成。C 相作為非換相相，電磁轉矩與非換相電流成正比，其方程:

高速運行下，電源電壓小于4 倍反電勢幅值。以換相時刻作為0 點，A 相電流下降快，B 相電流上升慢，使得C 相電流有波動，從而產生換相轉矩脈動。最大轉矩脈動在A 相電流降為0 時取得。

不同PWM 方式在開關管調制導通時電流回路一致，如圖2(a)所示，區別在于開關管調制關斷時續流回路不一致。其中HON-LPWM 和ON-PWM續流回路相同，HPWM -LON 和PWM -ON 續流回路相同。

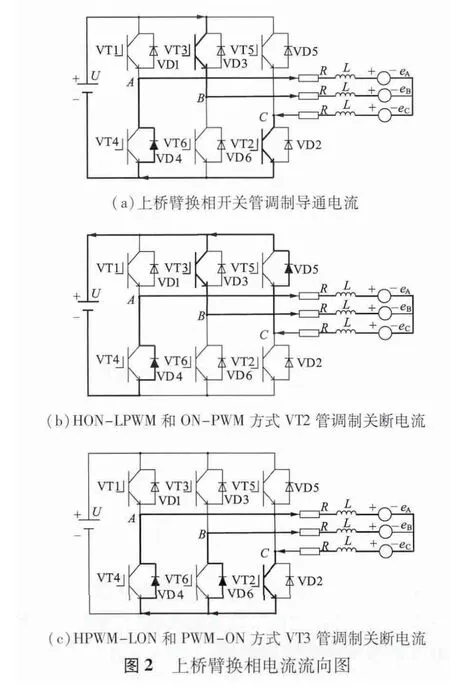
3.1.1 HON-LPWM 和ON-PWM 方式

VT2 管進行PWM 調制，VT3 管恒通。VT2 管調制關斷時電流回路如圖2(b)所示。三相端電壓方程:

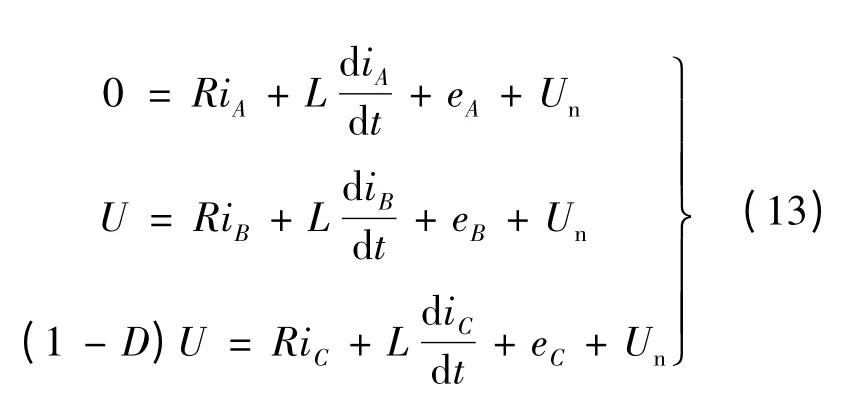
由式(13)解得三相電流方程:

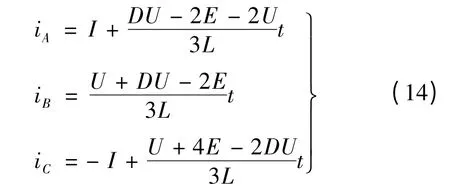
A 相電流降為0 的時間:

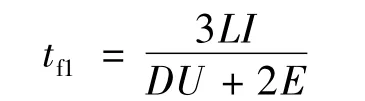
B 相電流上升到穩定值I 的時間:

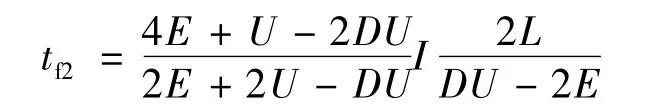
總的換相時間:

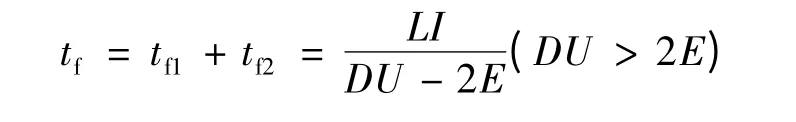
在A 相電流降為0 時刻，C 相電流:

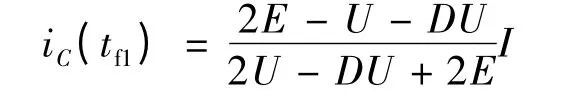
此時的電磁轉矩:

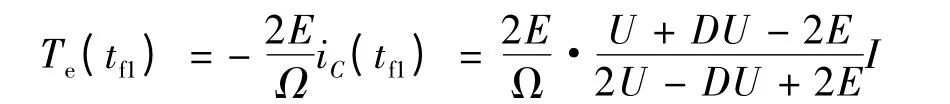
所以上橋臂換相HON -LPWM 和ON - PWM方式下的電磁轉矩脈動:

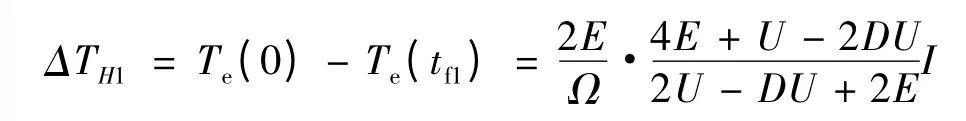
3.1.2 HPWM-LON 和PWM-ON 方式:

VT2 管恒通，VT3 管進行PWM 調制。VT3 管調制關斷時電流回路如圖2(c)。三相端電壓方程:

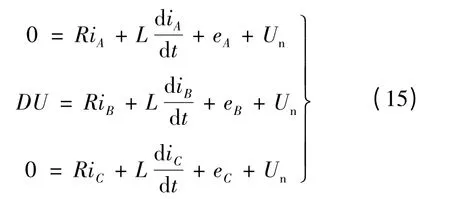
同樣的方法解得:

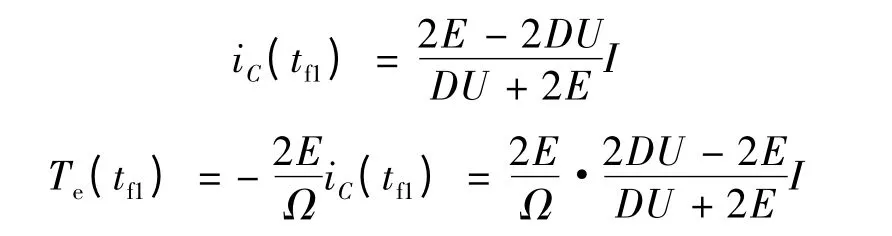
所以上橋臂換相HPWM -LON 和PWM - ON方式下的電磁轉矩脈動:

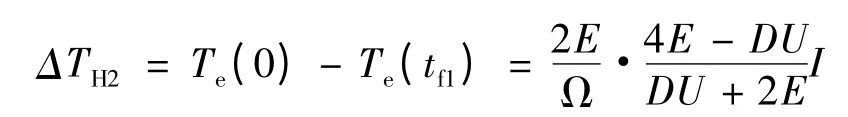
3.2 下橋臂換相

以AB 相換相到AC 相為例，電流的轉換通過關斷VT6，導通VT2 完成。A 相作為非換相相，電磁轉矩與非換相電流成正比，其方程:

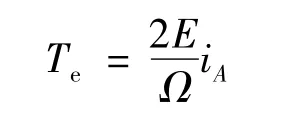
以換相時刻作為0 點，B 相電流下降快，C 相電流上升慢，A 相電流存在波動，從而產生換相轉矩脈動。最大轉矩脈動在B 相電流降為0 時取得。

不同PWM 方式在開關管調制導通時電流回路一致，如圖3(a)所示，區別在于調制關斷時續流回路不一致。其中HON-LPWM 和PWM-ON 續流回路相同，HPWM-LON 和ON-PWM 續流回路相同。

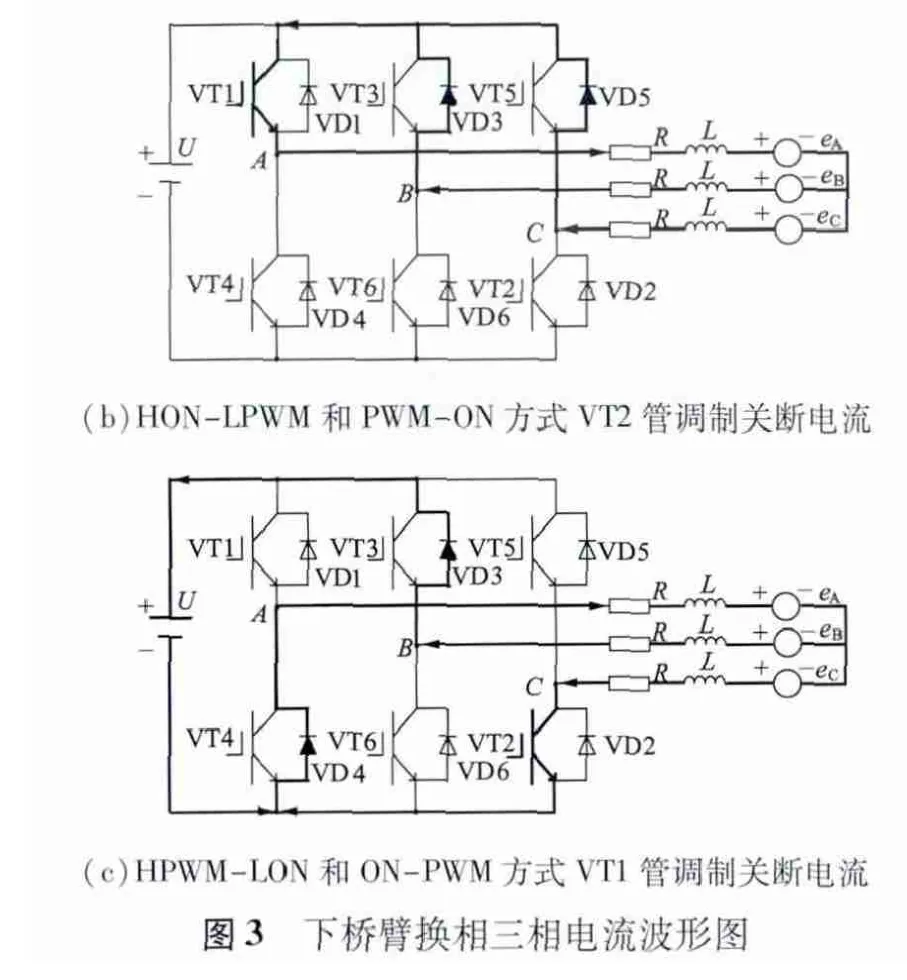
3.2.1 HON-LPWM 和PWM-ON 方式

VT2 管進行PWM 調制，VT1 管恒通。VT2 管調制關斷時電流回路如圖3(b)所示。三相端電壓方程:

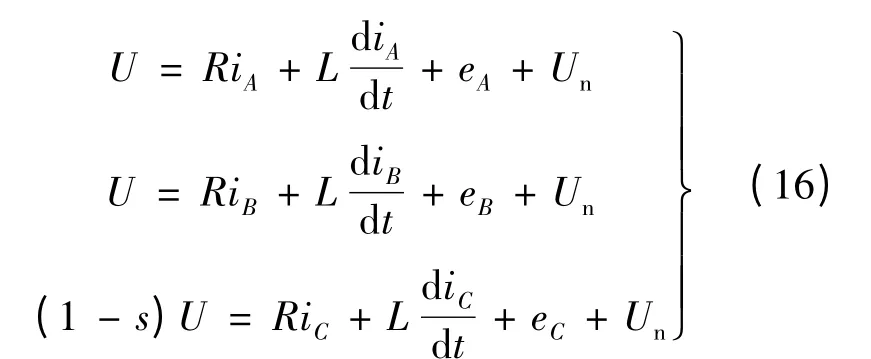
同樣的方法解得:

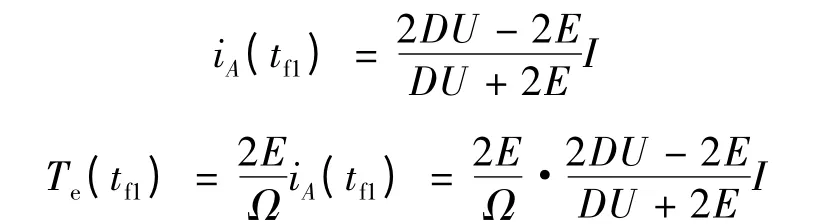
所以下橋臂換相HON -LPWM 和PWM -ON 方式下的電磁轉矩脈動:

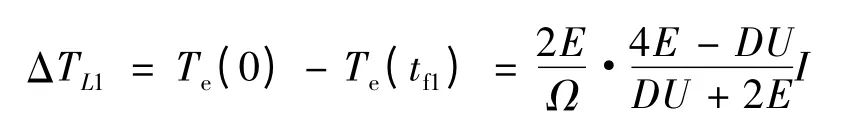
3.2.2 HPWM-LON 和ON-PWM 方式

VT2 管恒通，VT1 管進行PWM 調制。VT1 管調制關斷時電流回路如圖3(c)所示。三相端電壓方程:

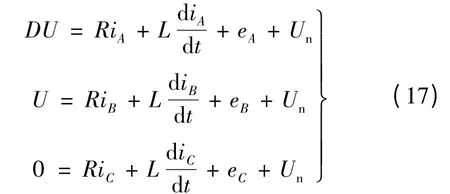
同樣的方法解得:

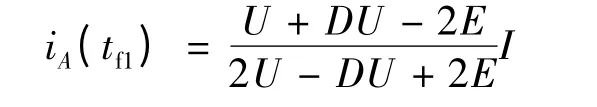
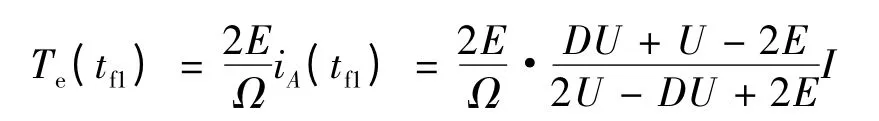
所以下橋臂換相HPWM -LON 和ON -PWM方式下的電磁轉矩脈動:

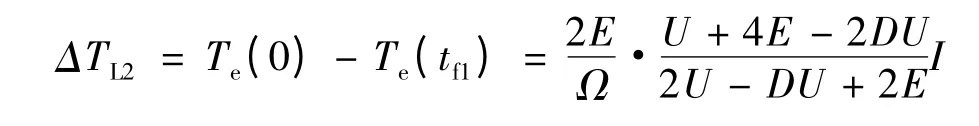
3.3 HPWM-LPWM 方式

雙斬方式上、下橋臂均調制，在上、下橋臂換相時效果一樣，故只分析上橋臂換相過程。仍以AC導通換相到BC 導通為例。則雙斬方式VT2 管，VT3 管均進行PWM 調制。

VT2，VT3 管調制導通時電流回路仍如圖2(a)所示，調制關斷時電流回路如圖4 所示。

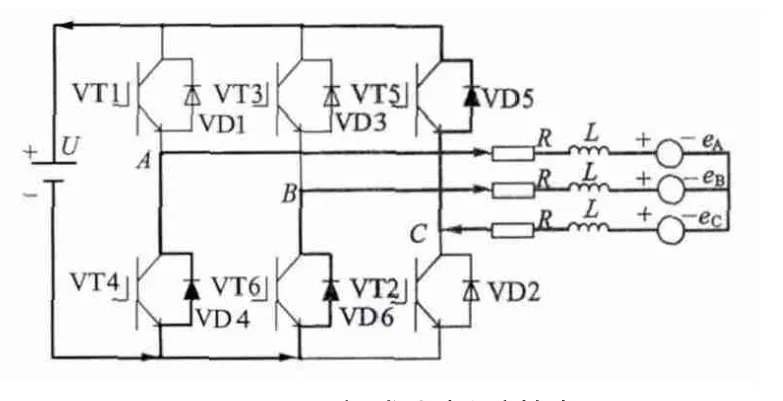
圖4 HPWM-LPWM 方式上橋臂換相VT2，VT3管調制關斷電流流向圖

三相端電壓方程:

同樣的方法解得:

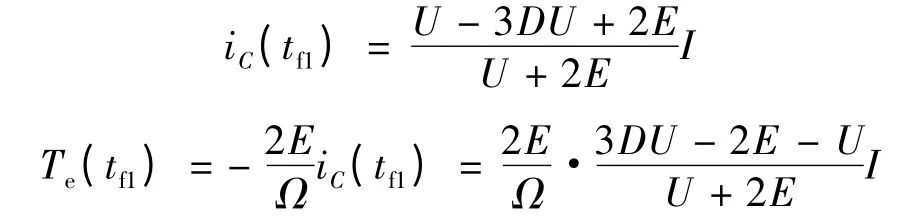
所以HPWM-LPWM 方式下電磁轉矩脈動:

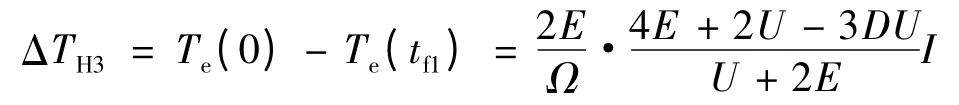
由以上分析，比較上橋臂換相轉矩脈動:

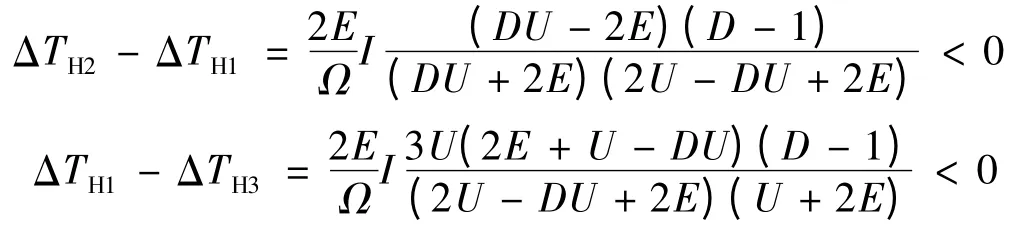
同理，比較下橋臂換相轉矩脈動:

所以ΔTH2＜ΔTH1＜ΔTH3，ΔTL1＜ΔTL2＜ΔTH3。由上述比較可得PWM-ON 方式有最小的換相轉矩脈動。

由于HPWM - LPWM 方式在開關管調制關斷時兩個電流回路均為二極管導通向電源回饋能量，其電流下降最快，電流波動最大，轉矩脈動也最大;而PWM-ON 方式在某一橋臂換相時保證了另一橋臂的開關管恒通，避免了電流回路里兩個二極管導通向電源回饋能量現象的發生，因此理論上其電流波動最小，轉矩脈動也最小;其它三種單斬方式在某橋臂換相開關管調制關斷時有一個電流回路存在兩個二極管導通向電源回饋能量的現象，其電流及轉矩脈動較小。因此原理上PWM-ON 方式有最小的換相轉矩脈動，HPWM -LPWM 方式有最大的換相轉矩脈動。原理分析與上述公式推導結論一致。

4 仿真結果及分析

在MATLAB/Simulink 下搭建無刷直流電動機仿真模型。仿真所用電機參數:額定功率3.7 kW，電源電壓300 V(DC)，額定轉速1 500 r/min，極對數p=4，電感0.188 4 mH，磁鏈大小為0.148 Wb，仿真中所加負載為TL=10 N·m。

圖5 為5 種不同PWM 調制方式在一個周期內的轉矩波形圖。設以AB 相導通作為一個周期6 個狀態的起始狀態，則圖5 中出現的6 個尖峰分別對應上、下橋臂換相。

由圖5 可知，在非換相過程，4 種單斬方式轉矩脈動大致相等;在上橋臂換相過程，HON-LPWM 和PWM-ON 方式轉矩脈動較小;在下橋臂換相過程，HPWM - LON 和PWM - ON 方式轉矩脈動較小;HPWM-LPWM 無論在非換相還是換相過程，轉矩脈動都較大，且諧波較大。綜合上述分析可得PWM-ON 方式有最小的轉矩脈動。與理論分析結果一致。

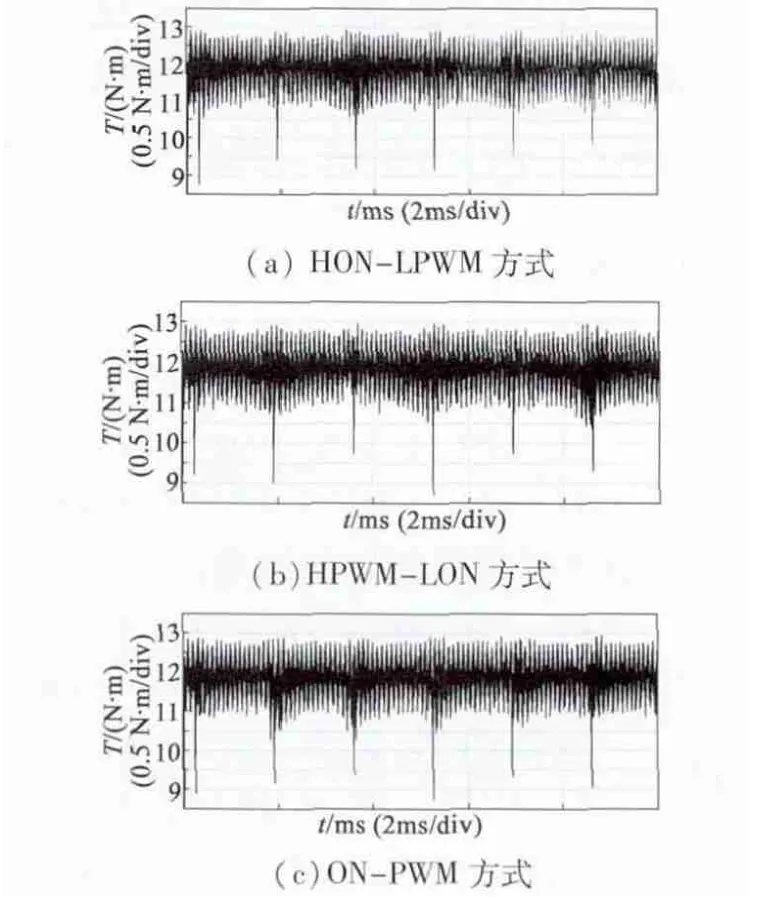
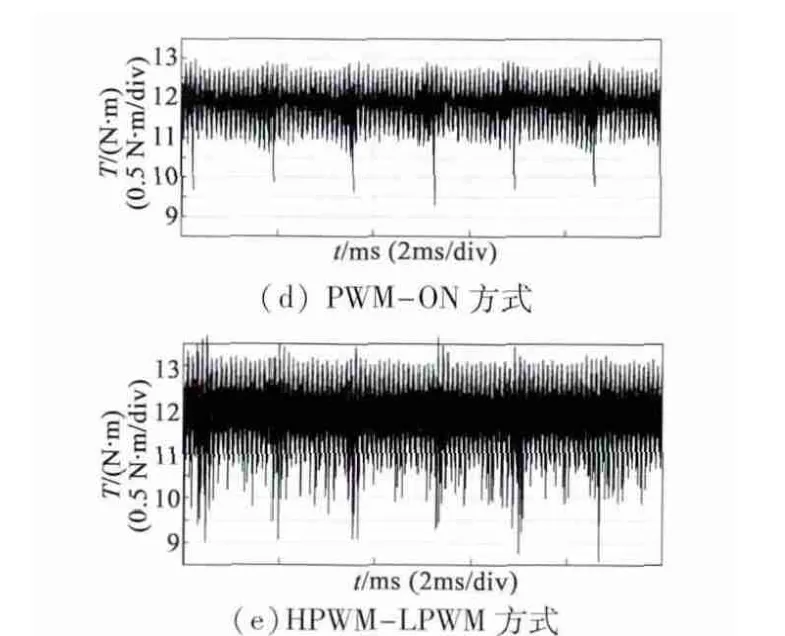
圖5 5 種PWM 方式下電磁轉矩仿真波形圖

5 結 語

本文從無刷直流電動機運行中的定子電流的非換相和換相過程出發，通過理論的公式推導，分析了HON-LPWM，HPWM-LON，ON-PWM，PWM-ON和HPWM-LPWM 5 種常用PWM 調制方式對無刷直流電動機轉矩脈動的影響，得出采用PWM -ON方式可使轉矩脈動最小。在此基礎上進行了原理分析，分析結果與公式推導結論一致。對無刷直流電動機在不同調制方式下進行了仿真研究，仿真結果驗證了理論分析的正確性。

［1］ 貢俊，陸國林.無刷直流電機在工業中的應用和發展［J］.微特電機，2000，28(5):15 -19.

［2］ XIA Chang -liang，WANG Ying -fa，SHI Ting -na.Implementation of finite-state model predictive control for commutation torque ripple minimization of permanent - magnet brushless DC motor［J］. IEEE Trans. on Industrial Electronics，2013，60(3):896-905.

［3］ CARLSON R.Analysis of torque ripple due to phase commutation in brushless dc machines［J］.IEEE Trans on. Industrial Applications，1992，28(3):632 -638.

［4］ SALAH W A，ISHAK D，HAMMADI K J.PWM switching strategy for torque ripple minimazation in BLDC motor［J］.Journal of Electrical Engineering，2011，62(3):141 -146.

［5］ 張相軍，陳伯時.無刷直流電機控制系統中PWM 調制方式對換相轉矩脈動的影響［J］.電機與控制學報，2003，7(2):87 -91.

［6］ 賀安超，劉衛國，郭志大.無刷直流電動機斬波方式與電磁轉矩脈動關系［J］.微特電機，2010，28(5):12 -15.

［7］ SHENG Tian-tian，WANG Xiao-lin，SHAN Tao.A new method to reduce both conduction and commutation torque ripple for BLDC machines［C］//17th ICEMS，2014:2975 -2980.

［8］ CHUANG H S，Yu-LungKe.Analysis of commutation torque ripple using different PWM modes in BLDC motors［C］//IEEE Industrial ＆Commercial Power Systems Technical Conference，2009:1 -6.

［9］ 周美蘭，高肇明，吳曉剛，等.五種PWM 方式對直流無刷電機系統換相轉矩脈動的影響［J］.電機與控制學報，2013，17(7):15 -21.

［10］ 賀虎成，劉衛國，郎寶華.開關頻率對無刷直流電機轉矩脈動的影響分析［J］.微電機，2008，41(7):1 -5.